高考全国卷文数试题

高考全国卷文数试题

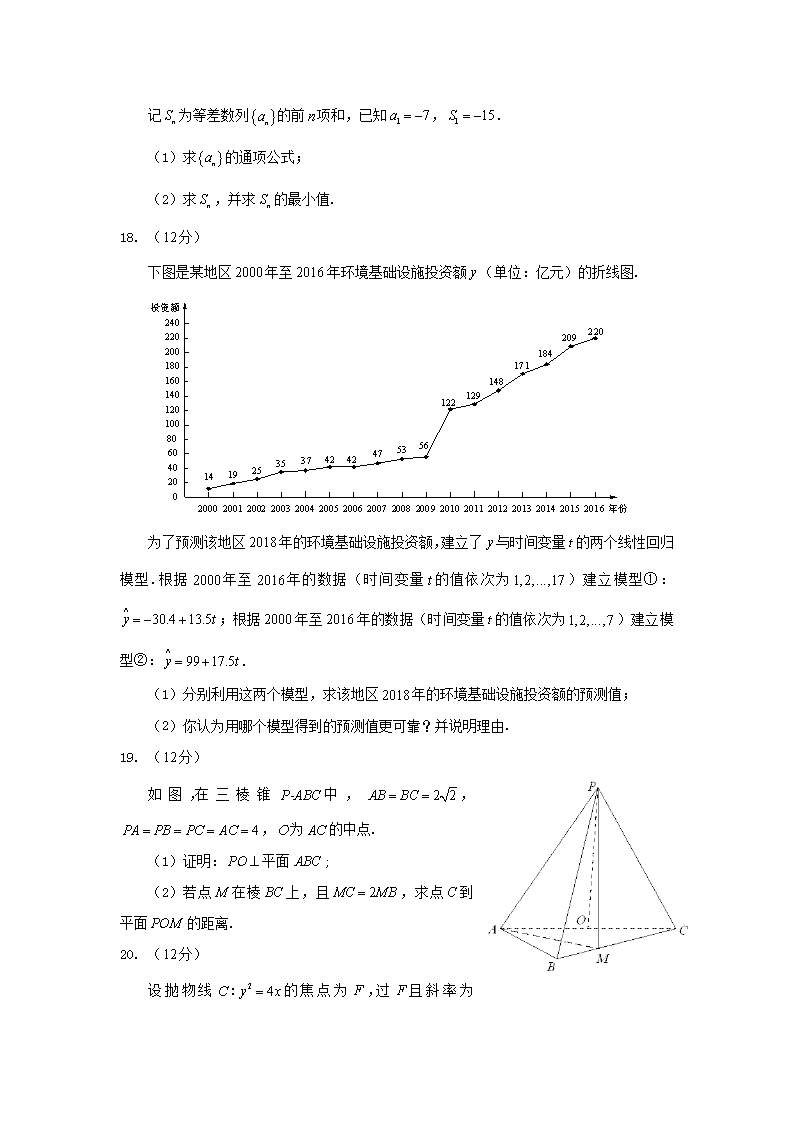
‎2018年普通高等学校招生全国统一考试II卷 文科数学 一、 选择题：本题共小题，每小题分，共分。在每小题给出的四个选项中，只有一项是符合题目要求的。‎ 1. A. B. C. D.‎ 2. 已知集合，，则 A. B. C. D.‎ 3. 函数的图像大致为 4. 已知向量满足，，则 A. B. C. D.‎ 5. 从名男同学和名女同学中任选人参加社区服务，则选中的人都是女同学的概率为 A. B. C. D.‎ 6. 双曲线的离心率为，则其渐近线方程为 A. B. C. D.‎ 7. 在中，，，，则 A. B. C. D.‎ 8. 为计算，设计了右侧的程序框图，则在空白框中应填入 A. ‎ B. ‎ C. ‎ D.‎ 1. 在正方体中，为棱的中点，则异面直线与所成角的正切值 为 A. B. C. D.‎ 2. 若在是减函数，则的最大值是 A. B. C. D.‎ 3. 已知是椭圆的两个焦点，是上的一点，若，且，则 的离心率为 A. B. C. D.‎ 4. 已知是定义域为的奇函数，满足，若，则 A. ‎ B. C. D.‎ 二、填空题：本题共小题，每小题分，共分。‎ 5. 曲线在点处的切线方程为 .‎ 6. 若满足约束条件则的最大值为 .‎ 7. 已知，则 .‎ 8. 已知圆锥的顶点为，母线互相垂直，与圆锥底面所成角为.若的 面积为，则该圆锥的体积为 .‎ 一、 解答题：共分。解答应写出文字说明、证明过程或演算步骤。第题为必考题。 每个试题考生都必须作答。第题为选考题，考生根据要求作答。‎ （一） 必考题：共分。‎ 9. ‎（分）‎ 记为等差数列的前项和，已知，.‎ （1） 求的通项公式；‎ （2） 求，并求的最小值.‎ 1. ‎（分）‎ 下图是某地区年至年环境基础设施投资额（单位：亿元）的折线图.‎ 为了预测该地区年的环境基础设施投资额，建立了与时间变量的两个线性回归模型.根据年至年的数据（时间变量的值依次为）建立模型①：；根据年至年的数据（时间变量的值依次为）建立模型②：.‎ （1） 分别利用这两个模型，求该地区年的环境基础设施投资额的预测值；‎ （2） 你认为用哪个模型得到的预测值更可靠？并说明理由.‎ 2. ‎（分）‎ 如图，在三棱锥中，，，为的中点.‎ （1） 证明：平面;‎ （2） 若点在棱上，且，求点到平面的距离.‎ 3. ‎（分）‎ 设抛物线:的焦点为，过且斜率为 的直线与交于，两点， .‎ （1） 求的方程；‎ （2） 求过点，两点且与的准线相切的圆的方程.‎ 1. ‎（分）‎ 已知函数.‎ （1） 若，求的单调区间；‎ （2） 证明：只有一个零点.‎ （一） 选考题：共分。请考生在第题中任选一题作答。如果多做，则按照所做的第 一题计分。‎ 2. ‎[选修：坐标系与参数方程]（分）‎ 在直角坐标系中，曲线的参数方程为（），直线的参数方 程为（）.‎ （1） 求和的直角坐标方程；‎ （2） 若曲线截直线所得线段中点坐标为，求的斜率.‎ 3. ‎[选修：不等式选讲]（分）‎ 设函数.‎ （1） 当时，求不等式的解集；‎ （2） 若，求的取值范围.‎