- 2021-05-13 发布 |
- 37.5 KB |
- 105页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
历年高考数学真题全国卷整理版
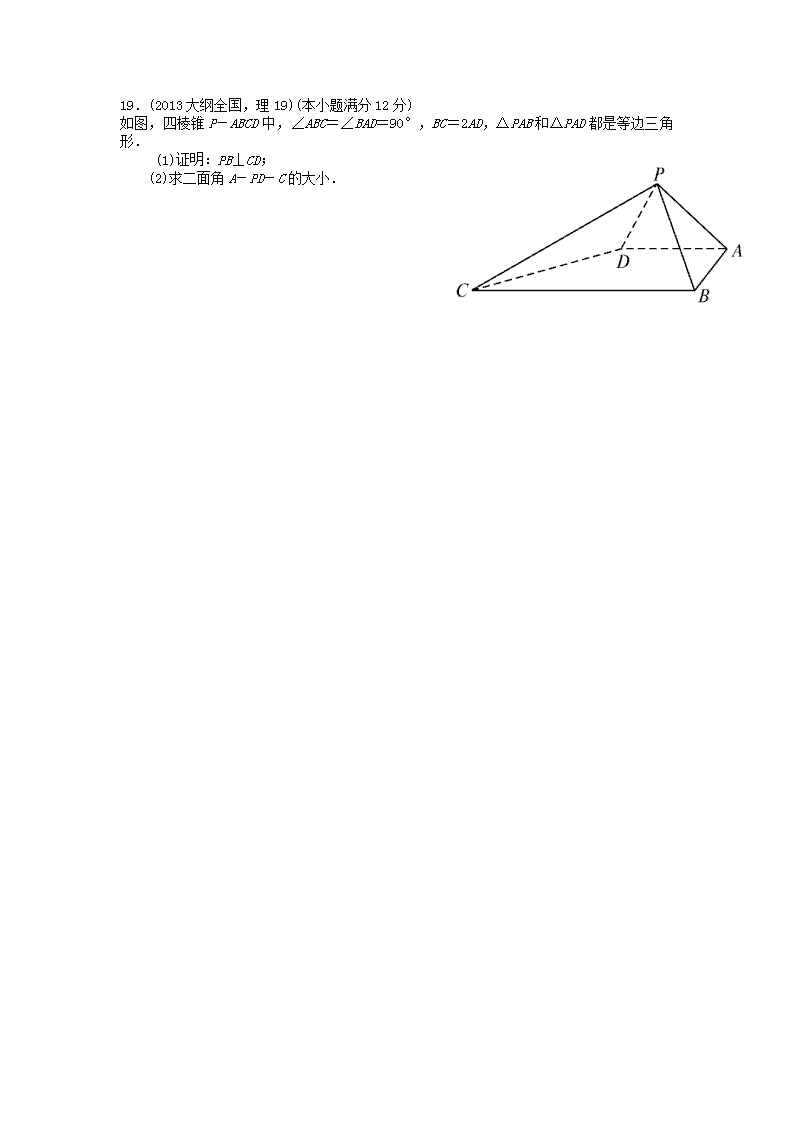
2013 年普通高等学校夏季招生全国统一考试数学理工农医类 (大纲全国卷) 一、选择题:本大题共 12 小题,每小题 5 分,在每小题给出的四个选项中,只有一项是符 合题目要求的. 1.(2013 大纲全国,理 1)设集合 A={1,2,3},B={4,5},M={x|x=a+b,a∈A,b∈B}, 则 M 中元素的个数为( ). A.3 B.4 C.5 D.6 2.(2013 大纲全国,理 2) 3(1+ 3i) =( ). A.-8 B.8 C.-8i D.8i 3.(2013 大纲全国,理 3)已知向量 m=(λ+1,1),n=(λ+2,2),若(m+n)⊥(m-n),则 λ=( ). A.-4 B.-3 C.-2 D.-1 4.(2013 大纲全国,理 4)已知函数 f(x)的定义域为(-1,0),则函数 f(2x+1)的定义域为 ( ). A.(-1,1) B. 11, 2 C.(-1,0) D. 1 ,1 2 5.(2013 大纲全国,理 5)函数 f(x)= 2 1log 1 x (x>0)的反函数 f-1 (x)=( ). A. 1 2 1x (x>0) B. 1 2 1x (x≠0) C.2x-1(x∈R) D.2x-1(x>0) 6.(2013 大纲全国,理 6)已知数列{an}满足 3an+1+an=0,a2= 4 3 ,则{an}的前 10 项和等 于( ). A.-6(1-3-10) B. 1 9 (1-310) C.3(1-3-10) D.3(1+3-10) 7.(2013 大纲全国,理 7)(1+x)8(1+y)4的展开式中 x2y2的系数是( ). A.56 B.84 C.112 D.168 8.(2013 大纲全国,理 8)椭圆 C: 22 =1 4 3 x y 的左、右顶点分别为 A1,A2,点 P 在 C 上且 直线 PA2斜率的取值范围是[-2,-1],那么直线 PA1斜率的取值范围是( ). A. 1 3, 2 4 B. 3 3, 8 4 C. 1 ,1 2 D. 3 ,1 4 9.(2013 大纲全国,理 9)若函数 f(x)=x2 +ax+ 1 x 在 1 , 2 是增函数,则 a 的取值范围 是( ). A.[-1,0] B.[-1,+∞) C.[0,3] D.[3,+∞) 10.(2013 大纲全国,理 10)已知正四棱柱 ABCD-A1B1C1D1中,AA1=2AB,则 CD 与平面 BDC1 所成角的正弦值等于( ). A. 2 3 B. 3 3 C. 2 3 D. 1 3 11.(2013 大纲全国,理 11)已知抛物线 C:y2 =8x 与点 M(-2,2),过 C 的焦点且斜率为 k 的直线与 C交于 A,B 两点.若 0MA MB ,则 k=( ). A. 1 2 B. 2 2 C. 2 D.2 12.(2013 大纲全国,理 12)已知函数 f(x)=cos xsin 2x,下列结论中错误的是( ). A.y=f(x)的图像关于点(π,0)中心对称 B.y=f(x)的图像关于直线 π= 2 x 对称 C.f(x)的最大值为 3 2 D.f(x)既是奇函数,又是周期函数 二、填空题:本大题共 4 小题,每小题 5 分. 13.(2013 大纲全国,理 13)已知α是第三象限角,sin α= 1 3 ,则 cot α=__________. 14.(2013 大纲全国,理 14)6 个人排成一行,其中甲、乙两人不相邻的不同排法共有 __________种.(用数字作答) 15.(2013 大纲全国,理 15)记不等式组 0, 3 4, 3 4 x x y x y 所表示的平面区域为 D.若直线 y =a(x+1)与 D 有公共点,则 a 的取值范围是__________. 16.(2013 大纲全国,理 16)已知圆 O和圆 K 是球 O 的大圆和小圆,其公共弦长等于球 O 的半径,OK= 3 2 ,且圆 O 与圆 K 所在的平面所成的一个二面角为 60°,则球 O 的表面积等 于__________. 三、解答题:解答应写出文字说明,证明过程或演算步骤. 17.(2013 大纲全国,理 17)(本小题满分 10 分)等差数列{an}的前 n 项和为 Sn.已知 S3= 2 2a , 且 S1,S2,S4成等比数列,求{an}的通项公式. 18.(2013 大纲全国,理 18)(本小题满分 12 分)设△ABC 的内角 A,B,C 的对边分别为 a,b, c,(a+b+c)(a-b+c)=ac. (1)求 B; (2)若 sin Asin C= 3 1 4 ,求 C. 19.(2013 大纲全国,理 19)(本小题满分 12 分) 如图,四棱锥 P-ABCD 中,∠ABC=∠BAD=90°,BC=2AD,△PAB 和△PAD 都是等边三角形. (1)证明:PB⊥CD; (2)求二面角 A-PD-C 的大小. 20.(2013 大纲全国,理 20)(本小题满分 12 分)甲、乙、丙三人进行羽毛球练习赛,其中两 人比赛,另一人当裁判,每局比赛结束时,负的一方在下一局当裁判.设各局中双方获胜的 概率均为 1 2 ,各局比赛的结果相互独立,第 1局甲当裁判. (1)求第 4 局甲当裁判的概率; (2)X 表示前 4 局中乙当裁判的次数,求 X 的数学期望. 21.(2013 大纲全国,理 21)(本小题满分 12 分)已知双曲线 C: 2 2 2 2 =1x y a b (a>0,b>0) 的左、右焦点分别为 F1,F2,离心率为 3,直线 y=2与 C的两个交点间的距离为 6 . (1)求 a,b; (2)设过 F2的直线 l 与 C的左、右两支分别交于 A,B 两点,且|AF1|=|BF1|,证明:|AF2|, |AB|,|BF2|成等比数列. 22.(2013 大纲全国,理 22)(本小题满分 12 分)已知函数 f(x)= 1ln(1+ ) 1 x xx x . (1)若 x≥0时,f(x)≤0,求λ的最小值; (2)设数列{an}的通项 1 1 1=1+ 2 3na n ,证明:a2n-an+ 1 4n >ln 2. 2013 年普通高等学校夏季招生全国统一考试数学理工农医类 (大纲全国卷) 一、选择题:本大题共 12 小题,每小题 5 分,在每小题给出的四个选项中,只有一项是符 合题目要求的. 1. 答案:B 解析:由题意知 x=a+b,a∈A,b∈B,则 x 的可能取值为 5,6,7,8.因此集合 M 共有 4个元 素.故选 B. 2. 答案:A 解析: 3 2 3(1+ 3i) =13 3i+3( 3i) +( 3i) = 8 .故选 A. 3. 答案:B 解析:由(m+n)⊥(m-n)⇒|m|2 -|n|2 =0⇒(λ+1) 2 +1-[(λ+2) 2 +4]=0⇒λ=-3.故选 B. 4. 答案:B 解析:由题意知-1<2x+1<0,则-1<x< 1 2 .故选 B. 5. 答案:A 解析:由题意知 11+ x =2y⇒x= 1 2 1y (y>0), 因此 f-1 (x)= 1 2 1x (x>0).故选 A. 6. 答案:C 解析:∵3an+1+an=0,∴an+1= 1 3 na .∴数列{an}是以 1 3 为公比的等比数列.∵a2= 4 3 , ∴a1=4. ∴S10= 1014 1 3 11 3 =3(1-3 -10 ).故选 C. 7. 答案:D 解析:因为(1+x)8的展开式中 x2的系数为 2 8C ,(1+y)4的展开式中 y2的系数为 2 4C ,所以 x2y2 的系数为 2 2 8 4C C 168 .故选 D. 8. 答案:B 解析:设 P 点坐标为(x0,y0),则 2 2 0 0 =1 4 3 x y , 2 0 0 2PA yk x , 1 0 0 2PA yk x ,于是 1 2 2 2 0 0 2 2 2 0 0 33 34 2 4 4PA PA xyk k x x . 故 1 2 3 1 4PA PA k k =- . ∵ 2PAk ∈[-2,-1], ∴ 1 3 3, 8 4PAk .故选 B. 9. 答案:D 解析:由条件知 f′(x)=2x+a- 2 1 x ≥0 在 1 , 2 上恒成立,即 2 1 2a x x 在 1 , 2 上恒成立.∵函数 2 1 2y x x 在 1 , 2 上为减函数,∴ max 2 1 1< 2 3 21 2 y .∴a≥3. 故选 D. 10. 答案:A 解析:如下图,连结 AC 交 BD 于点 O,连结 C1O,过 C作 CH⊥C1O 于点 H. ∵ 1 1 BD AC BD AA AC AA A 1 1 1 1 BD ACC A CH ACC A 平面 平面 1 1 = CH BD CH CO BD CO O CH⊥平面 C1BD, ∴∠HDC 为 CD 与平面 BDC1所成的角. 设 AA1=2AB=2,则 2= = 2 2 ACOC , 2 2 2 2 1 1 2 9 3= 2 = = 2 2 22 CO OC CC . 由等面积法,得 C1O·CH=OC·CC1,即 3 2 2 2 2 2 CH = , ∴ 2= 3 CH . ∴sin∠HDC= 2 23= = 1 3 HC DC .故选 A. 11. 答案:D 解析:由题意知抛物线 C 的焦点坐标为(2,0),则直线 AB 的方程为 y=k(x-2),将其代入 y2=8x,得 k2x2-4(k2+2)x+4k2=0. 设 A(x1,y1),B(x2,y2),则 x1+x2= 2 2 4 2k k ,x1x2=4.① 由 1 1 2 2 2 2 y k x y k x 1 2 1 2 2 1 2 1 2 1 2 4 , [ 2 4]. y y k x x k y y k x x x x ① ② ∵ 0MA MB , ∴(x1+2,y1-2)·(x2+2,y2-2)=0. ∴(x1+2)(x2+2)+(y1-2)(y2-2)=0, 即 x1x2+2(x1+x2)+4+y1y2-2(y1+y2)+4=0.④ 由①②③④解得 k=2.故选 D. 12. 答案:C 解析:由题意知 f(x)=2cos2x·sin x=2(1-sin2x)sin x. 令 t=sin x,t∈[-1,1], 则 g(t)=2(1-t2)t=2t-2t3. 令 g′(t)=2-6t2 =0,得 3= 3 t . 当 t=±1 时,函数值为 0; 当 3 3 t 时,函数值为 4 3 9 ; 当 3 3 t 时,函数值为 4 3 9 . ∴g(t)max= 4 3 9 , 即 f(x)的最大值为 4 3 9 .故选 C. 二、填空题:本大题共 4小题,每小题 5 分. 13.答案: 2 2 解析:由题意知 cos α= 2 1 2 21 sin 1 9 3 . 故 cot α= cos =2 2 sin . 14.答案:480 解析:先排除甲、乙外的 4 人,方法有 4 4A 种,再将甲、乙插入这 4 人形成的 5个间隔中, 有 2 5A 种排法,因此甲、乙不相邻的不同排法有 4 2 4 5A A 480 (种). 15.答案: 1 ,4 2 解析:作出题中不等式组表示的可行域如图中阴影部分所示. ∵直线y=a(x+1)过定点C(-1,0),由图并结合题意可知 1 2BCk , kAC=4, ∴要使直线 y=a(x+1)与平面区域 D 有公共点, 则 1 2 ≤a≤4. 16.答案:16π 解析:如下图,设 MN 为两圆的公共弦,E为 MN 的中点, 则 OE⊥MN,KE⊥MN,结合题意可知∠OEK=60°. 又 MN=R,∴△OMN 为正三角形.∴OE= 3 2 R . 又 OK⊥EK,∴ 3 2 =OE·sin 60°= 3 3 2 2 R . ∴R=2. ∴S=4πR2 =16π. 三、解答题:解答应写出文字说明,证明过程或演算步骤. 17.解:设{an}的公差为 d. 由 S3= 2 2a 得 3a2= 2 2a ,故 a2=0或 a2=3. 由 S1,S2,S4成等比数列得 2 2S =S1S4. 又 S1=a2-d,S2=2a2-d,S4=4a2+2d, 故(2a2-d)2 =(a2-d)(4a2+2d). 若 a2=0,则 d2 =-2d2 ,所以 d=0,此时 Sn=0,不合题意; 若 a2=3,则(6-d)2 =(3-d)(12+2d),解得 d=0 或 d=2. 因此{an}的通项公式为 an=3 或 an=2n-1. 18. 解:(1)因为(a+b+c)(a-b+c)=ac,所以 a2+c2-b2=-ac. 由余弦定理得 cos B= 2 2 2 1 2 2 a c b ac , 因此 B=120°. (2)由(1)知 A+C=60°, 所以 cos(A-C)=cos Acos C+sin Asin C=cos Acos C-sin Asin C+2sin Asin C=cos(A +C)+2sin Asin C= 1 3 1 3+2 2 4 2 , 故 A-C=30°或 A-C=-30°, 因此 C=15°或 C=45°. 19. (1)证明:取 BC 的中点 E,连结 DE,则 ABED 为正方形. 过 P 作 PO⊥平面 ABCD,垂足为 O. 连结 OA,OB,OD,OE. 由△PAB 和△PAD 都是等边三角形知 PA=PB=PD, 所以 OA=OB=OD,即点 O为正方形 ABED 对角线的交点, 故 OE⊥BD,从而 PB⊥OE. 因为 O是 BD 的中点,E 是 BC 的中点, 所以 OE∥CD.因此 PB⊥CD. (2)解法一:由(1)知 CD⊥PB,CD⊥PO,PB∩PO=P, 故 CD⊥平面 PBD. 又 PD平面 PBD,所以 CD⊥PD. 取 PD 的中点 F,PC 的中点 G,连结 FG, 则 FG∥CD,FG⊥PD. 连结 AF,由△APD 为等边三角形可得 AF⊥PD. 所以∠AFG 为二面角 A-PD-C的平面角. 连结 AG,EG,则 EG∥PB. 又 PB⊥AE,所以 EG⊥AE. 设 AB=2,则 AE= 2 2 ,EG= 1 2 PB=1, 故 AG= 2 2AE EG =3. 在△AFG 中,FG= 1 2 2 CD , 3AF ,AG=3, 所以 cos∠AFG= 2 2 2 6 2 3 FG AF AG FG AF . 因此二面角 A-PD-C 的大小为 6π arccos 3 . 解法二:由(1)知,OE,OB,OP 两两垂直. 以 O 为坐标原点,OE 的方向为 x 轴的正方向建立如图所示的空间直角坐标系 O-xyz. 设| AB |=2,则 A( 2 ,0,0),D(0, 2 ,0),C( 2 2 , 2 ,0),P(0,0, 2 ). PC =( 2 2 , 2 , 2 ), PD =(0, 2 , 2 ). AP =( 2 ,0, 2 ), AD =( 2 , 2 ,0). 设平面 PCD 的法向量为 n1=(x,y,z),则 n1· PC =(x,y,z)·( 2 2 , 2 , 2 )=0, n1·PD =(x,y,z)·(0, 2 , 2 )=0, 可得 2x-y-z=0,y+z=0. 取 y=-1,得 x=0,z=1,故 n1=(0,-1,1). 设平面 PAD 的法向量为 n2=(m,p,q),则 n2· AP =(m,p,q)·( 2 ,0, 2 )=0,n2· AD =(m,p,q)·( 2 , 2 ,0)=0,可得 m+q=0,m-p=0. 取 m=1,得 p=1,q=-1,故 n2=(1,1,-1). 于是 cos〈n1,n2〉= 1 2 1 2 6 | || | 3 ·n n n n . 由于〈n1,n2〉等于二面角 A-PD-C的平面角,所以二面角 A-PD-C的大小为 6π arccos 3 . 20. 解:(1)记 A1表示事件“第 2 局结果为甲胜”, A2表示事件“第 3 局甲参加比赛时,结果为甲负”,A 表示事件“第 4 局甲当裁判”. 则 A=A1·A2. P(A)=P(A1·A2)=P(A1)P(A2)= 1 4 . (2)X 的可能取值为 0,1,2. 记A3表示事件“第3局乙和丙比赛时,结果为乙胜丙”,B1表示事件“第1局结果为乙胜丙”, B2表示事件“第 2 局乙和甲比赛时,结果为乙胜甲”,B3表示事件“第 3局乙参加比赛时, 结果为乙负”. 则 P(X=0)=P(B1·B2·A3)=P(B1)P(B2)·P(A3)= 1 8 ,P(X=2)=P( 1B ·B3)=P( 1B )P(B3)= 1 4 ,P(X=1)=1-P(X=0)-P(X=2)= 1 1 51 8 4 8 ,EX=0·P(X=0)+1·P(X=1)+ 2·P(X=2)= 9 8 . 21. (1)解:由题设知 c a =3,即 2 2 2 a b a =9,故 b2 =8a2 . 所以 C的方程为 8x2-y2=8a2. 将 y=2 代入上式,求得 2 1 2 x a . 由题设知, 2 12 6 2 a ,解得 a2 =1. 所以 a=1,b= 2 2 . (2)证明:由(1)知,F1(-3,0),F2(3,0),C 的方程为 8x2 -y2 =8.① 由题意可设 l 的方程为 y=k(x-3), <2 2k ,代入①并化简得(k2-8)x2-6k2x+9k2+8 =0. 设 A(x1,y1),B(x2,y2),则 x1≤-1,x2≥1,x1+x2= 2 2 6 8 k k ,x1·x2= 2 2 9 8 8 k k . 于是|AF1|= 2 2 1 13x y = 2 2 1 13 8 8x x =-(3x1+1), |BF1|= 2 2 2 23x y = 2 2 2 23 8 8x x =3x2+1. 由|AF1|=|BF1|得-(3x1+1)=3x2+1,即 x1+x2= 2 3 . 故 2 2 6 2 8 3 k k ,解得 k2= 4 5 ,从而 x1·x2= 19 9 . 由于|AF2|= 2 2 1 13x y = 2 2 1 13 8 8x x =1-3x1, |BF2|= 2 2 2 23x y = 2 2 2 23 8 8x x =3x2-1, 故|AB|=|AF2|-|BF2|=2-3(x1+x2)=4,|AF2|·|BF2|=3(x1+x2)-9x1x2-1=16. 因而|AF2|·|BF2|=|AB|2,所以|AF2|,|AB|,|BF2|成等比数列. 22. (1)解:由已知 f(0)=0,f′(x)= 2 2 1 2 1 x x x ,f′(0)=0. 若 1 2 ,则当 0<x<2(1-2λ)时,f′(x)>0,所以 f(x)>0. 若 1 2 ,则当 x>0 时,f′(x)<0,所以当 x>0 时,f(x)<0. 综上,λ的最小值是 1 2 . (2)证明:令 1 2 .由(1)知,当 x>0 时,f(x)<0, 即 2 ln(1 ) 2 2 x x x x . 取 1x k ,则 2 1 1>ln 2 1 k k k k k . 于是 2 1 2 1 1 1 4 2 2( 1) n n n k n a a n k k = 2 1 2 12 1 1ln 2 1 n n k n k n k k k k k =ln 2n-ln n=ln 2. 所以 2 1 ln 2 4n na a n . 2013 年普通高等学校夏季招生全国统一考试数学理工农医类 (全国新课标卷 I) 第Ⅰ卷 一、选择题:本大题共 12 小题,每小题 5 分,在每小题给出的四个选项中,只有一项是符 合题目要求的. 1.(2013 课标全国Ⅰ,理 1)已知集合 A={x|x2 -2x>0},B={x|- 5 <x< 5 },则( ). A.A∩B= B.A∪B=R C.B A D.A B 2.(2013 课标全国Ⅰ,理 2)若复数 z 满足(3-4i)z=|4+3i|,则 z 的虚部为( ). A.-4 B. 4 5 C.4 D. 4 5 3.(2013 课标全国Ⅰ,理 3)为了解某地区的中小学生的视力情况,拟从该地区的中小学生 中抽取部分学生进行调查,事先已了解到该地区小学、初中、高中三个学段学生的视力情况 有较大差异,而男女生视力情况差异不大.在下面的抽样方法中,最合理的抽样方法是( ). A.简单随机抽样 B.按性别分层抽样 C.按学段分层抽样 D.系统 抽样 4.(2013 课标全国Ⅰ,理 4)已知双曲线 C: 2 2 2 2 =1x y a b (a>0,b>0)的离心率为 5 2 , 则 C 的渐近线方程为( ). A.y= 1 4 x B.y= 1 3 x C.y= 1 2 x D.y=±x 5.(2013 课标全国Ⅰ,理 5)执行下面的程序框图,如果输入的 t∈[-1,3],则输出 的 s 属于( ). A.[-3,4] B.[-5,2] C.[-4,3] D.[-2,5] 6.(2013 课标全国Ⅰ,理 6)如图,有一个水平放置的透明无盖的正方体容器,容器高 8 cm, 将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为 6 cm,如 果不计容器的厚度,则球的体积为( ). A. 500π 3 cm3 B. 866π 3 cm3 C. 1372π 3 cm3 D. 2048π 3 cm3 7.(2013 课标全国Ⅰ,理 7)设等差数列{an}的前 n 项和为 Sn,若 Sm-1=-2,Sm=0,Sm+1=3, 则 m=( ). A.3 B.4 C.5 D.6 8.(2013 课标全国Ⅰ,理 8)某几何体的三视图如图所示,则该 几何体的体积为( ). A.16+8π B.8+8π C.16+16π D.8+16π 9.(2013 课标全国Ⅰ,理 9)设 m 为正整数,(x+y)2m 展开式的二项式系数的最大值为 a,(x +y)2m+1展开式的二项式系数的最大值为 b.若 13a=7b,则 m=( ). A.5 B.6 C.7 D.8 10.(2013 课标全国Ⅰ,理 10)已知椭圆 E: 2 2 2 2 =1x y a b (a>b>0)的右焦点为 F(3,0),过 点 F 的直线交 E于 A,B 两点.若 AB 的中点坐标为(1,-1),则 E的方程为( ). A. 2 2 =1 45 36 x y B. 2 2 =1 36 27 x y C. 2 2 =1 27 18 x y D. 2 2 =1 18 9 x y 11.(2013 课标全国Ⅰ,理 11)已知函数 f(x)= 2 2 0 ln( 1) 0. x x x x x , , , 若|f(x)|≥ax,则 a 的 取值范围是( ). A.(-∞,0] B.(-∞,1] C.[-2,1] D.[-2,0] 12.(2013 课标全国Ⅰ,理 12)设△AnBnCn的三边长分别为 an,bn,cn,△AnBnCn的面积为 Sn, n=1,2,3,….若 b1>c1,b1+c1=2a1,an+1=an,bn+1= 2 n nc a ,cn+1= 2 n nb a ,则( ). A.{Sn}为递减数列 B.{Sn}为递增数列 C.{S2n-1}为递增数列,{S2n}为递减数列 D.{S2n-1}为递减数列,{S2n}为 递增数列 第Ⅱ卷 本卷包括必考题和选考题两部分.第(13)题~第(21)题为必考题,每个试题考生都必须做 答.第(22)题~第(24)题为选考题,考生根据要求做答. 二、填空题:本大题共 4小题,每小题 5 分. 13.(2013 课标全国Ⅰ,理 13)已知两个单位向量 a,b 的夹角为 60°,c=ta+(1-t)b. 若 b·c=0,则 t=__________. 14.(2013 课标全国Ⅰ,理 14)若数列{an}的前 n 项和 2 1 3 3n nS a ,则{an}的通项公 式是 an=_______. 15.(2013 课标全国Ⅰ,理 15)设当 x=θ时,函数 f(x)=sin x-2cos x 取得最大值, 则 cos θ=__________. 16.(2013 课标全国Ⅰ,理 16)若函数 f(x)=(1-x2)(x2+ax+b)的图像关于直线 x= -2 对称,则 f(x)的最大值为__________. 三、解答题:解答应写出文字说明,证明过程或演算步骤. 17.(2013 课标全国Ⅰ,理 17)(本小题满分 12 分)如图,在△ABC 中,∠ABC=90°,AB= 3 , BC=1,P 为△ABC 内一点,∠BPC=90°. (1)若 PB= 1 2 ,求 PA; (2)若∠APB=150°,求 tan∠PBA. 18.(2013 课标全国Ⅰ,理 18)(本小题满分 12 分)如图,三棱柱 ABC-A1B1C1中,CA=CB, AB=AA1,∠BAA1=60°. (1)证明:AB⊥A1C; (2)若平面 ABC⊥平面 AA1B1B,AB=CB,求直线 A1C 与平面 BB1C1C 所成角的正弦值. 19.(2013 课标全国Ⅰ,理 19)(本小题满分 12 分)一批产品需要进行质量检验,检验方案是: 先从这批产品中任取 4 件作检验,这 4 件产品中优质品的件数记为 n.如果 n=3,再从这批 产品中任取 4 件作检验,若都为优质品,则这批产品通过检验;如果 n=4,再从这批产品 中任取 1 件作检验,若为优质品,则这批产品通过检验;其他情况下,这批产品都不能通过 检验. 假设这批产品的优质品率为 50%,即取出的每件产品是优质品的概率都为 1 2 ,且各件产品是 否为优质品相互独立. (1)求这批产品通过检验的概率; (2)已知每件产品的检验费用为 100 元,且抽取的每件产品都需要检验,对这批产品作质量 检验所需的费用记为 X(单位:元),求 X 的分布列及数学期望. 20.(2013 课标全国Ⅰ,理 20)(本小题满分 12 分)已知圆 M:(x+1)2+y2=1,圆 N:(x-1)2 +y2 =9,动圆 P与圆 M 外切并且与圆 N内切,圆心 P的轨迹为曲线 C. (1)求 C 的方程; (2)l 是与圆 P,圆 M 都相切的一条直线,l 与曲线 C 交于 A,B两点,当圆 P 的半径最长时, 求|AB|. 21.(2013 课标全国Ⅰ,理 21)(本小题满分 12 分)设函数 f(x)=x2 +ax+b,g(x)=e x (cx+ d).若曲线 y=f(x)和曲线 y=g(x)都过点 P(0,2),且在点 P处有相同的切线 y=4x+2. (1)求 a,b,c,d 的值; (2)若 x≥-2 时,f(x)≤kg(x),求 k 的取值范围. 请考生在第(22)、(23)、(24)三题中任选一题做答.注意:只能做所选定的题目.如果多做, 则按所做的第一个题目计分,做答时请用 2B 铅笔在答题卡上将所选题号后的方框涂黑. 22.(2013 课标全国Ⅰ,理 22)(本小题满分 10 分)选修 4—1:几何证明选讲 如图,直线 AB 为圆的切线,切点为 B,点 C 在圆上,∠ABC 的角平分线 BE 交圆于点 E,DB 垂直 BE 交圆于点 D. (1)证明:DB=DC; (2)设圆的半径为 1,BC= 3 ,延长 CE 交 AB 于点 F,求△BCF 外接圆的半径. 23.(2013 课标全国Ⅰ,理 23)(本小题满分 10 分)选修 4—4:坐标系与参数方程 已知曲线 C1的参数方程为 4 5cos , 5 5sin x t y t (t 为参数),以坐标原点为极点,x 轴的正半轴为 极轴建立极坐标系,曲线 C2的极坐标方程为ρ=2sin θ. (1)把 C1的参数方程化为极坐标方程; (2)求 C1与 C2交点的极坐标(ρ≥0,0≤θ<2π). 24.(2013 课标全国Ⅰ,理 24)(本小题满分 10 分)选修 4—5:不等式选讲:已知函数 f(x) =|2x-1|+|2x+a|,g(x)=x+3. (1)当 a=-2 时,求不等式 f(x)<g(x)的解集; (2)设 a>-1,且当 x∈ 1, 2 2 a 时,f(x)≤g(x),求 a 的取值范围. 2013 年普通高等学校夏季招生全国统一考试数学理工农医类 (全国卷 I 新课标) 第Ⅰ卷 一、选择题:本大题共 12 小题,每小题 5 分,在每小题给出的四个选项中,只有一项是符 合题目要求的. 1. 答案:B 解析:∵x(x-2)>0,∴x<0或 x>2. ∴集合 A 与 B 可用图象表示为: 由图象可以看出 A∪B=R,故选 B. 2. 答案:D 解析:∵(3-4i)z=|4+3i|, ∴ 5 5(3 4i) 3 4 i 3 4i (3 4i)(3 4i) 5 5 z . 故 z 的虚部为 4 5 ,选 D. 3. 答案:C 解析:因为学段层次差异较大,所以在不同学段中抽取宜用分层抽样. 4. 答案:C 解析:∵ 5 2 ce a ,∴ 2 2 2 2 2 2 5 4 c a be a a . ∴a2 =4b2 , 1= 2 b a . ∴渐近线方程为 1 2 by x x a . 5. 答案:A 解析:若 t∈[-1,1),则执行 s=3t,故 s∈[-3,3). 若 t∈[1,3],则执行 s=4t-t2 ,其对称轴为 t=2. 故当 t=2 时,s取得最大值 4.当 t=1或 3时,s 取得最小值 3,则 s∈[3,4]. 综上可知,输出的 s∈[-3,4].故选 A. 6. 答案:A 解析:设球半径为 R,由题可知 R,R-2,正方体棱长一半可构成直角三角形,即△OBA 为 直角三角形,如图. BC=2,BA=4,OB=R-2,OA=R, 由 R2=(R-2)2+42,得 R=5, 所以球的体积为 34 500π5 π 3 3 (cm 3 ),故选 A. 7. 答案:C 解析:∵Sm-1=-2,Sm=0,Sm+1=3, ∴am=Sm-Sm-1=0-(-2)=2,am+1=Sm+1-Sm=3-0=3. ∴d=am+1-am=3-2=1. ∵Sm=ma1+ 1 2 m m ×1=0,∴ 1 1 2 ma . 又∵am+1=a1+m×1=3,∴ 1 3 2 m m . ∴m=5.故选 C. 8. 答案:A 解析:由三视图可知该几何体为半圆柱上放一个长方体,由图中数据可知圆柱底面半径 r= 2,长为 4,在长方体中,长为 4,宽为 2,高为 2,所以几何体的体积为πr2×4× 1 2 +4×2×2 =8π+16.故选 A. 9. 答案:B 解析:由题意可知,a= 2Cm m,b= 2 1Cm m , 又∵13a=7b,∴ 2 ! 2 1 !13 =7 ! ! ! 1 ! m m m m m m , 即 13 2 1 7 1 m m .解得 m=6.故选 B. 10. 答案:D 解析:设 A(x1,y1),B(x2,y2),∵A,B 在椭圆上, ∴ 2 2 1 1 2 2 2 2 2 2 2 2 1, 1, x y a b x y a b ① ② ①-②,得 1 2 1 2 1 2 1 2 2 2 =0x x x x y y y y a b , 即 2 1 2 1 2 2 1 2 1 2 = y y y yb a x x x x , ∵AB 的中点为(1,-1),∴y1+y2=-2,x1+x2=2, 而 1 2 1 2 y y x x =kAB= 0 1 1= 3 1 2 ,∴ 2 2 1= 2 b a . 又∵a2 -b2 =9,∴a2 =18,b2 =9. ∴椭圆 E 的方程为 2 2 =1 18 9 x y .故选 D. 11. 答案:D 解析:由 y=|f(x)|的图象知: ①当 x>0 时,y=ax 只有 a≤0 时,才能满足|f(x)|≥ax,可排除 B,C. ②当 x≤0 时,y=|f(x)|=|-x2 +2x|=x2 -2x. 故由|f(x)|≥ax 得 x2 -2x≥ax. 当 x=0 时,不等式为 0≥0 成立. 当 x<0 时,不等式等价于 x-2≤a. ∵x-2<-2,∴a≥-2. 综上可知:a∈[-2,0]. 12. 答案:B 第Ⅱ卷 本卷包括必考题和选考题两部分.第(13)题~第(21)题为必考题,每个试题考生都必须做 答.第(22)题~第(24)题为选考题,考生根据要求做答. 二、填空题:本大题共 4 小题,每小题 5 分. 13.答案:2 解析:∵c=ta+(1-t)b, ∴b·c=ta·b+(1-t)|b|2. 又∵|a|=|b|=1,且 a 与 b 夹角为 60°,b⊥c, ∴0=t|a||b|cos 60°+(1-t), 0= 1 2 t+1-t. ∴t=2. 14.答案:(-2) n-1 解析:∵ 2 1 3 3n nS a ,① ∴当 n≥2 时, 1 1 2 1 3 3n nS a .② ①-②,得 1 2 2 3 3n n na a a , 即 1 n n a a =-2. ∵a1=S1= 1 2 1 3 3 a , ∴a1=1. ∴{an}是以 1 为首项,-2 为公比的等比数列,an=(-2) n-1 . 15.答案: 2 5 5 解析:f(x)=sin x-2cos x = 1 25 sin cos 5 5 x x , 令 cos α= 1 5 ,sin α= 2 5 , 则 f(x)= 5 sin(α+x), 当 x=2kπ+ π 2 -α(k∈Z)时,sin(α+x)有最大值 1,f(x)有最大值 5 , 即θ=2kπ+ π 2 -α(k∈Z), 所以 cos θ= πcos 2 π+ 2 k = πcos 2 =sin α= 2 2 5 55 . 16.答案:16 解析:∵函数 f(x)的图像关于直线 x=-2对称, ∴f(x)满足 f(0)=f(-4),f(-1)=f(-3), 即 15 16 4 , 0 8 9 3 , b a b a b 解得 8, 15. a b ∴f(x)=-x4 -8x3 -14x2 +8x+15. 由 f′(x)=-4x3 -24x2 -28x+8=0, 得 x1=-2- 5 ,x2=-2,x3=-2+ 5 . 易知,f(x)在(-∞,-2- 5 )上为增函数,在(-2- 5 ,-2)上为减函数,在(-2,- 2+ 5 )上为增函数,在(-2+ 5 ,+∞)上为减函数. ∴f(-2- 5 )=[1-(-2- 5 ) 2 ][(-2- 5 ) 2 +8(-2- 5 )+15] =(-8- 4 5 )(8- 4 5 ) =80-64=16. f(-2)=[1-(-2) 2 ][(-2) 2 +8×(-2)+15] =-3(4-16+15) =-9. f(-2+ 5 )=[1-(-2+ 5 )2][(-2+ 5 )2+8(-2+ 5 )+15] =(-8+ 4 5 )(8+ 4 5 ) =80-64=16. 故 f(x)的最大值为 16. 三、解答题:解答应写出文字说明,证明过程或演算步骤. 17. 解:(1)由已知得∠PBC=60°,所以∠PBA=30°. 在△PBA 中,由余弦定理得 PA2 = 1 1 73 2 3 cos 30 4 2 4 . 故 PA= 7 2 . (2)设∠PBA=α,由已知得 PB=sin α. 在△PBA 中,由正弦定理得 3 sin sin150 sin(30 ) , 化简得 3 cos α=4sin α. 所以 tan α= 3 4 ,即 tan∠PBA= 3 4 . 18. (1)证明:取 AB 的中点 O,连结 OC,OA1,A1B. 因为 CA=CB,所以 OC⊥AB. 由于 AB=AA1,∠BAA1=60°, 故△AA1B 为等边三角形, 所以 OA1⊥AB. 因为 OC∩OA1=O,所以 AB⊥平面 OA1C. 又 A1C平面 OA1C,故 AB⊥A1C. (2)解:由(1)知 OC⊥AB,OA1⊥AB. 又平面 ABC⊥平面 AA1B1B,交线为 AB, 所以 OC⊥平面 AA1B1B, 故 OA,OA1,OC 两两相互垂直. 以 O 为坐标原点,OA 的方向为 x 轴的正方向,|OA |为单位长,建立如图所示的空间直角 坐标系 O-xyz. 由题设知 A(1,0,0),A1(0, 3 ,0),C(0,0, 3 ),B(-1,0,0). 则 BC =(1,0, 3 ), 1BB = 1AA =(-1, 3 ,0), 1AC =(0, 3 , 3 ). 设 n=(x,y,z)是平面 BB1C1C 的法向量, 则 1 0, 0, BC BB n n 即 3 0, 3 0. x z x y 可取 n=( 3 ,1,-1). 故 cos〈n, 1AC 〉= 1 1 AC AC n n = 10 5 . 所以 A1C 与平面 BB1C1C 所成角的正弦值为 10 5 . 19. 解:(1)设第一次取出的 4 件产品中恰有 3 件优质品为事件 A1,第一次取出的 4 件产品全是 优质品为事件 A2,第二次取出的 4 件产品都是优质品为事件 B1,第二次取出的 1 件产品是优 质品为事件 B2,这批产品通过检验为事件 A,依题意有 A=(A1B1)∪(A2B2),且 A1B1与 A2B2互 斥,所以 P(A)=P(A1B1)+P(A2B2) =P(A1)P(B1|A1)+P(A2)P(B2|A2) = 4 1 1 1 3 16 16 16 2 64 . (2)X 可能的取值为 400,500,800,并且 P(X=400)= 4 1 111 16 16 16 ,P(X=500)= 1 16 ,P(X=800)= 1 4 . 所以 X的分布列为 X 400 500 800 P 11 16 1 16 1 4 EX= 11 1 1400 +500 +800 16 16 4 =506.25. 20. 解:由已知得圆 M 的圆心为 M(-1,0),半径 r1=1;圆 N的圆心为 N(1,0),半径 r2=3. 设圆 P的圆心为 P(x,y),半径为 R. (1)因为圆 P 与圆 M 外切并且与圆 N 内切, 所以|PM|+|PN|=(R+r1)+(r2-R)=r1+r2=4. 由椭圆的定义可知,曲线 C 是以 M,N为左、右焦点,长半轴长为 2,短半轴长为 3 的椭圆 (左顶点除外),其方程为 2 2 =1 4 3 x y (x≠-2). (2)对于曲线 C 上任意一点 P(x,y),由于|PM|-|PN|=2R-2≤2, 所以 R≤2,当且仅当圆 P的圆心为(2,0)时,R=2. 所以当圆 P的半径最长时,其方程为(x-2) 2 +y2 =4. 若 l 的倾斜角为 90°,则 l 与 y 轴重合,可得|AB|= 2 3 . 若 l的倾斜角不为90°,由r1≠R知 l不平行于x轴,设l与 x轴的交点为Q,则 1 | | | | QP R QM r , 可求得 Q(-4,0),所以可设 l:y=k(x+4). 由 l 与圆 M相切得 2 | 3 | =1 1 k k , 解得 k= 2 4 . 当 k= 2 4 时,将 2 2 4 y x 代入 2 2 =1 4 3 x y , 并整理得 7x2 +8x-8=0, 解得 x1,2= 4 6 2 7 . 所以|AB|= 2 2 1 181 | | 7 k x x . 当 2 4 k 时,由图形的对称性可知|AB|= 18 7 . 综上,|AB|= 2 3 或|AB|= 18 7 . 21. 解:(1)由已知得 f(0)=2,g(0)=2,f′(0)=4,g′(0)=4. 而 f′(x)=2x+a,g′(x)=e x (cx+d+c), 故 b=2,d=2,a=4,d+c=4. 从而 a=4,b=2,c=2,d=2. (2)由(1)知,f(x)=x2 +4x+2,g(x)=2e x (x+1). 设函数 F(x)=kg(x)-f(x)=2kex(x+1)-x2-4x-2, 则 F′(x)=2kex (x+2)-2x-4=2(x+2)(kex -1). 由题设可得 F(0)≥0,即 k≥1. 令 F′(x)=0 得 x1=-ln k,x2=-2. ①若 1≤k<e2,则-2<x1≤0.从而当 x∈(-2,x1)时,F′(x)<0;当 x∈(x1,+∞)时,F′(x) >0.即 F(x)在(-2,x1)单调递减,在(x1,+∞)单调递增.故 F(x)在[-2,+∞)的最小值 为 F(x1). 而 F(x1)=2x1+2- 2 1x -4x1-2=-x1(x1+2)≥0. 故当 x≥-2 时,F(x)≥0,即 f(x)≤kg(x)恒成立. ②若 k=e 2 ,则 F′(x)=2e 2 (x+2)(e x -e -2 ). 从而当 x>-2 时,F′(x)>0,即 F(x)在(-2,+∞)单调递增. 而 F(-2)=0,故当 x≥-2 时,F(x)≥0,即 f(x)≤kg(x)恒成立. ③若 k>e 2 ,则 F(-2)=-2ke-2 +2=-2e -2 (k-e 2 )<0. 从而当 x≥-2 时,f(x)≤kg(x)不可能恒成立. 综上,k 的取值范围是[1,e 2 ]. 请考生在第(22)、(23)、(24)三题中任选一题做答.注意:只能做所选定的题目.如果多做, 则按所做的第一个题目计分,做答时请用 2B 铅笔在答题卡上将所选题号后的方框涂黑. 22. (1)证明:连结 DE,交 BC 于点 G. 由弦切角定理得,∠ABE=∠BCE. 而∠ABE=∠CBE,故∠CBE=∠BCE,BE=CE. 又因为 DB⊥BE, 所以 DE 为直径,∠DCE=90°, 由勾股定理可得 DB=DC. (2)解:由(1)知,∠CDE=∠BDE,DB=DC, 故 DG 是 BC 的中垂线,所以 BG= 3 2 . 设 DE 的中点为 O,连结 BO,则∠BOG=60°. 从而∠ABE=∠BCE=∠CBE=30°, 所以 CF⊥BF,故 Rt△BCF 外接圆的半径等于 3 2 . 23. 解:(1)将 4 5cos , 5 5sin x t y t 消去参数 t,化为普通方程(x-4) 2 +(y-5) 2 =25, 即 C1:x2 +y2 -8x-10y+16=0. 将 cos , sin x y 代入 x2+y2-8x-10y+16=0 得 ρ2 -8ρcos θ-10ρsin θ+16=0. 所以 C1的极坐标方程为 ρ2-8ρcos θ-10ρsin θ+16=0. (2)C2的普通方程为 x2 +y2 -2y=0. 由 2 2 2 2 8 10 16 0, 2 0 x y x y x y y 解得 1, 1 x y 或 0, 2. x y 所以 C1与 C2交点的极坐标分别为 π2, 4 , π2, 2 . 24. 解:(1)当 a=-2 时,不等式 f(x)<g(x)化为|2x-1|+|2x-2|-x-3<0. 设函数 y=|2x-1|+|2x-2|-x-3, 则 y= 15 , , 2 12, 1, 2 3 6, 1. x x x x x x 其图像如图所示.从图像可知,当且仅当 x∈(0,2)时,y<0. 所以原不等式的解集是{x|0<x<2}. (2)当 x∈ 1, 2 2 a 时,f(x)=1+a. 不等式 f(x)≤g(x)化为 1+a≤x+3. 所以 x≥a-2 对 x∈ 1, 2 2 a 都成立. 故 2 a ≥a-2,即 4 3 a . 从而 a的取值范围是 41, 3 . 2013 年普通高等学校夏季招生全国统一考试数学理工农医类 (全国新课标卷 II) 第Ⅰ卷 一、选择题:本大题共 12小题,每小题 5分,在每小题给出的四个选项中,只 有一项是符合题目要求的. 1.(2013 课标全国Ⅱ,理 1)已知集合 M={x|(x-1)2<4,x∈R},N={-1,0,1,2,3},则 M∩N=( ). A.{0,1,2} B.{-1,0,1,2} C.{-1,0,2,3} D.{0,1,2,3} 2.(2013 课标全国Ⅱ,理 2)设复数 z 满足(1-i)z=2i,则 z=( ). A.-1+i B.-1-I C.1+i D.1-i 3.(2013 课标全国Ⅱ,理 3)等比数列{an}的前 n 项和为 Sn.已知 S3=a2+10a1,a5=9,则 a1 =( ). A. 1 3 B. 1 3 C. 1 9 D. 1 9 4.(2013 课标全国Ⅱ,理 4)已知 m,n 为异面直线,m⊥平面α,n⊥平面β.直线 l 满足 l ⊥m,l⊥n,l α,l β,则( ). A.α∥β且 l∥α B.α⊥β且 l⊥β C.α与β相交,且交线垂直于 l D.α与β相交,且交线平行于 l 5.(2013课标全国Ⅱ,理5)已知(1+ax)(1+x)5 的展开式中x2 的系数为5,则a=( ). A.-4 B.-3 C.-2 D.-1 6.(2013 课标全国Ⅱ,理 6)执行下面的程序框图,如果输入的 N=10,那么输出的 S =( ). A. 1 1 11+ 2 3 10 B. 1 1 11+ 2! 3! 10! C. 1 1 11+ 2 3 11 D. 1 1 11+ 2! 3! 11! 7.(2013 课标全国Ⅱ,理 7)一个四面体的顶点在空间直角坐标系 O-xyz 中的坐标分别是 (1,0,1),(1,1,0),(0,1,1),(0,0,0),画该四面体三视图中的正视图时,以 zOx 平面为投 影面,则得到的正视图可以为( ). 8.(2013 课标全国Ⅱ,理 8)设 a=log36,b=log510,c=log714,则( ). A.c>b>a B.b>c>a C.a>c>b D.a>b>c 9.(2013 课标全国Ⅱ,理 9)已知 a>0,x,y 满足约束条件 1, 3, 3 . x x y y a x 若 z=2x+y 的最 小值为 1,则 a=( ). A. 1 4 B. 1 2 C.1 D.2 10.(2013 课标全国Ⅱ,理 10)已知函数 f(x)=x3 +ax2 +bx+c,下列结论中错误的是( ). A. x0∈R,f(x0)=0 B.函数 y=f(x)的图像是中心对称图形 C.若 x0 是 f(x)的极小值点,则 f(x)在区间(-∞,x0)单调递减 D.若 x0 是 f(x)的极值点,则 f′(x0)=0 11.(2013 课标全国Ⅱ,理 11)设抛物线 C:y2 =2px(p>0)的焦点为 F,点 M 在 C 上,|MF| =5,若以 MF 为直径的圆过点(0,2),则 C 的方程为( ). A.y2=4x 或 y2=8x B.y2=2x 或 y2=8x C.y2=4x 或 y2=16x D.y2=2x 或 y2=16x 12.(2013 课标全国Ⅱ,理 12)已知点 A(-1,0),B(1,0),C(0,1),直线 y=ax+b(a>0) 将△ABC 分割为面积相等的两部分,则 b 的取值范围是( ). A.(0,1) B. 2 11 , 2 2 C. 2 11 , 2 3 D. 1 1, 3 2 第Ⅱ卷 本卷包括必考题和选考题两部分,第 13 题~第 21 题为必考题,每个试题考生都必须做答。 第 22 题~第 24 题为选考题,考生根据要求做答。 二、填空题:本大题共 4小题,每小题 5 分. 13.(2013 课标全国Ⅱ,理 13)已知正方形 ABCD 的边长为 2,E 为 CD 的中点,则 AE BD =__________. 14.(2013 课标全国Ⅱ,理 14)从 n 个正整数 1,2,…,n中任意取出两个不同的数,若 取出的两数之和等于 5 的概率为 1 14 ,则 n=__________. 15.(2013 课标全国Ⅱ,理 15)设θ为第二象限角,若 π 1tan 4 2 ,则 sin θ+cos θ=__________. 16.(2013 课标全国Ⅱ,理 16)等差数列{an}的前 n项和为 Sn,已知 S10=0,S15=25,则 nSn的最小值为__________. 三、解答题:解答应写出文字说明,证明过程或演算步骤. 17.(2013 课标全国Ⅱ,理 17)(本小题满分 12 分)△ABC 的内角 A,B,C 的对边分别为 a,b, c,已知 a=bcos C+csin B. (1)求 B; (2)若 b=2,求△ABC 面积的最大值. 18.(2013 课标全国Ⅱ,理 18)(本小题满分 12 分)如图,直三棱柱 ABC-A1B1C1中,D,E 分 别是 AB,BB1的中点,AA1=AC=CB= 2 2 AB . (1)证明:BC1∥平面 A1CD; (2)求二面角 D-A1C-E 的正弦值. 19.(2013 课标全国Ⅱ,理 19)(本小题满分 12 分)经销商经销某种农产品,在一个销售季度 内,每售出 1 t 该产品获利润 500 元,未售出的产品,每 1 t 亏损 300 元.根据历史资料, 得到销售季度内市场需求量的频率分布直方图,如图所示.经销商为下一个销售季度购进了 130 t 该农产品.以 X(单位:t,100≤X≤150)表示下一个销售季度内的市场需求量,T(单位: 元)表示下一个销售季度内经销该农产品的利润. (1)将 T 表示为 X 的函数; (2)根据直方图估计利润 T 不少于 57 000 元的概率; (3)在直方图的需求量分组中,以各组的区间中点值代表该组的各个值,并以需求量落入该 区间的频率作为需求量取该区间中点值的概率(例如:若需求量 X∈[100,110),则取 X=105, 且 X=105 的概率等于需求量落入[100,110)的频率), 求 T 的数学期望. 20.(2013 课标全国Ⅱ,理 20)(本小题满分 12 分)平面直角坐标系 xOy 中,过椭圆 M: 2 2 2 2 =1x y a b (a>b>0)右焦点的直线 3 0x y 交 M 于 A,B 两点,P 为 AB 的中点,且 OP 的斜率为 1 2 . (1)求 M 的方程; (2)C,D 为 M 上两点,若四边形 ACBD 的对角线 CD⊥AB,求四边形 ACBD 面积的最大值. 21.(2013 课标全国Ⅱ,理 21)(本小题满分 12 分)已知函数 f(x)=e x -ln(x+m). (1)设 x=0是 f(x)的极值点,求 m,并讨论 f(x)的单调性; (2)当 m≤2时,证明 f(x)>0. 请考生在第 22、23、24 题中任选择一题作答,如果多做,则按所做的第一题计分,做答时 请写清题号. 22.(2013 课标全国Ⅱ,理 22)(本小题满分 10 分)选修 4—1:几何证明选讲 如图,CD 为△ABC 外接圆的切线,AB 的延长线交直线 CD 于点 D,E,F 分别为弦 AB 与弦 AC 上的点,且 BC·AE=DC·AF,B,E,F,C 四点共圆. (1)证明:CA 是△ABC 外接圆的直径; (2)若 DB=BE=EA,求过 B,E,F,C 四点的圆的面积与△ABC 外接圆面积的比值. 23.(2013 课标全国Ⅱ,理 23)(本小题满分 10 分)选修 4—4:坐标系与参数方程 已知动点 P,Q都在曲线 C: 2cos , 2sin x t y t (t 为参数)上,对应参数分别为 t=α与 t=2α(0 <α<2π),M为 PQ 的中点. (1)求 M 的轨迹的参数方程; (2)将 M 到坐标原点的距离 d 表示为α的函数,并判断 M 的轨迹是否过坐标原点. 24.(2013 课标全国Ⅱ,理 24)(本小题满分 10 分)选修 4—5:不等式选讲 设 a,b,c均为正数,且 a+b+c=1,证明: (1)ab+bc+ac≤ 1 3 ; (2) 2 2 2 1a b c b c a . 2013 年普通高等学校夏季招生全国统一考试数学理工农医类 (全国新课标卷 II) 第Ⅰ卷 一、选择题:本大题共 12小题,每小题 5分,在每小题给出的四个选项中,只 有一项是符合题目要求的. 1. 答案:A 解析:解不等式(x-1)2<4,得-1<x<3,即 M={x|-1<x<3}.而 N={-1,0,1,2,3}, 所以 M∩N={0,1,2},故选 A. 2. 答案:A 解析: 2i 2i 1 i= 1 i 1 i 1 i z = 2 2i 2 =-1+i. 3. 答案:C 解析:设数列{an}的公比为 q,若 q=1,则由 a5=9,得 a1=9,此时 S3=27,而 a2+10a1= 99,不满足题意,因此 q≠1. ∵q≠1时,S3= 3 1(1 ) 1 a q q =a1·q+10a1, ∴ 31 1 q q =q+10,整理得 q2 =9. ∵a5=a1·q4 =9,即 81a1=9,∴a1= 1 9 . 4. 答案:D 解析:因为 m⊥α,l⊥m,l α,所以 l∥α.同理可得 l∥β. 又因为 m,n 为异面直线,所以α与β相交,且 l 平行于它们的交线.故选 D. 5. 答案:D 解析:因为(1+x)5 的二项展开式的通项为 5Cr rx (0≤r≤5,r∈Z),则含 x2 的项为 2 2 5C x + ax· 1 5C x=(10+5a)x2 ,所以 10+5a=5,a=-1. 6. 答案:B 解析:由程序框图知,当 k=1,S=0,T=1 时,T=1,S=1; 当 k=2 时, 1 2 T , 1=1+ 2 S ; 当 k=3 时, 1 2 3 T , 1 11+ 2 2 3 S ; 当 k=4 时, 1 2 3 4 T , 1 1 11+ 2 2 3 2 3 4 S ;…; 当 k=10 时, 1 2 3 4 10 T , 1 1 11+ 2! 3! 10! S ,k 增加 1 变为 11,满足 k >N,输出 S,所以 B正确. 7. 答案:A 解析:如图所示,该四面体在空间直角坐标系 O-xyz 的图像为下图: 则它在平面 zOx 上的投影即正视图为 ,故选 A. 8. 答案:D 解析:根据公式变形, lg 6 lg 21 lg3 lg3 a , lg10 lg 21 lg5 lg5 b , lg14 lg 21 lg 7 lg 7 c ,因 为 lg 7>lg 5>lg 3,所以 lg 2 lg 2 lg 2 lg 7 lg5 lg3 ,即 c<b<a.故选 D. 9. 答案:B 解析:由题意作出 1, 3 x x y 所表示的区域如图阴影部分所示, 作直线2x+y=1,因为直线2x+y=1与直线x=1的交点坐标为(1 -1),结合题意知直线 y=a(x-3)过点(1,-1),代入得 1 2 a , 所以 1 2 a . 10. 答案:C 解析:∵x0是 f(x)的极小值点,则 y=f(x)的图像大致如下图所示,则在 (-∞,x0)上不单调,故 C 不正确. 11. 答案:C 解析:设点 M 的坐标为(x0,y0),由抛物线的定义,得|MF|=x0+ 2 p =5, 则 x0=5- 2 p . 又点 F的坐标为 ,0 2 p ,所以以 MF 为直径的圆的方程为(x-x0) 2 px +(y-y0)y=0. 将 x=0,y=2 代入得 px0+8-4y0=0,即 2 0 2 y -4y0+8=0,所以 y0=4. 由 2 0y =2px0,得16 2 5 2 pp ,解之得 p=2,或 p=8. 所以 C的方程为 y2 =4x 或 y2 =16x.故选 C. 12. 答案:B 第Ⅱ卷 本卷包括必考题和选考题两部分,第 13 题~第 21 题为必考题,每个试题考生都必须做答。 第 22 题~第 24 题为选考题,考生根据要求做答。 二、填空题:本大题共 4小题,每小题 5 分. 13.答案:2 解析:以 AB 所在直线为 x 轴,AD 所在直线为 y 轴建立平面直角坐标系, 如图所示,则点A的坐标为(0,0),点B的坐标为(2,0),点D的坐标为(0,2) 点 E 的坐标为(1,2),则 AE =(1,2),BD =(-2,2),所以 2AE BD . 14.答案:8 解析:从 1,2,…,n 中任取两个不同的数共有 2Cn 种取法,两数之和为 5 的有(1,4),(2,3)2 种,所以 2 2 1 C 14n ,即 2 4 1 1 1 14 2 n n n n ,解 得 n=8. 15.答案: 10 5 解析:由 π 1 tan 1tan 4 1 tan 2 ,得 tan θ= 1 3 ,即 sin θ= 1 3 cos θ. 将其代入 sin 2θ+cos 2θ=1,得 210 cos 1 9 . 因为θ为第二象限角,所以 cos θ= 3 10 10 ,sin θ= 10 10 ,sin θ+cos θ= 10 5 . 16.答案:-49 解析:设数列{an}的首项为 a1,公差为 d,则 S10= 1 10 910 2 a d + =10a1+45d=0,① S15= 1 15 1415 2 a d =15a1+105d=25.② 联立①②,得 a1=-3, 2 3 d , 所以 Sn= 2( 1) 2 1 103 2 3 3 3 n nn n n . 令 f(n)=nSn,则 3 21 10( ) 3 3 f n n n , 2 20'( ) 3 f n n n . 令 f′(n)=0,得 n=0 或 20 3 n . 当 20 3 n 时,f′(n)>0, 200< < 3 n 时,f′(n)<0,所以当 20 3 n 时,f(n)取最小值,而 n∈N+,则 f(6)=-48,f(7)=-49,所以当 n=7 时,f(n)取最小值-49. 三、解答题:解答应写出文字说明,证明过程或演算步骤. 17. 解:(1)由已知及正弦定理得 sin A=sin Bcos C+sin Csin B.① 又 A=π-(B+C),故 sin A=sin(B+C)=sin Bcos C+cos Bsin C.② 由①,②和 C∈(0,π)得 sin B=cos B, 又 B∈(0,π),所以 π 4 B . (2)△ABC 的面积 1 2sin 2 4 S ac B ac . 由已知及余弦定理得 4=a2+c2- π2 cos 4 ac . 又 a2 +c2 ≥2ac,故 4 2 2 ac ,当且仅当 a=c 时,等号成立. 因此△ABC 面积的最大值为 2+1. 18. 解:(1)连结 AC1交 A1C 于点 F,则 F 为 AC1中点. 又 D 是 AB 中点,连结 DF,则 BC1∥DF. 因为 DF⊂平面 A1CD,BC1 平面 A1CD, 所以 BC1∥平面 A1CD. (2)由 AC=CB= 2 2 AB得,AC⊥BC. 以 C 为坐标原点,CA 的方向为 x 轴正方向,建立如图所示的空间直角坐标系 C-xyz. 设 CA=2,则 D(1,1,0),E(0,2,1),A1(2,0,2),CD =(1,1,0),CE =(0,2,1), 1CA =(2,0,2). 设 n=(x1,y1,z1)是平面 A1CD 的法向量, 则 1 0, 0, CD CA n n 即 1 1 1 1 0, 2 2 0. x y x z 可取 n=(1,-1,-1). 同理,设 m是平面 A1CE 的法向量, 则 1 0, 0, CE CA m m 可取 m=(2,1,-2). 从而 cos〈n,m〉= 3 | || | 3 ·n m n m , 故 sin〈n,m〉= 6 3 . 即二面角 D-A1C-E 的正弦值为 6 3 . 19. 解:(1)当 X∈[100,130)时,T=500X-300(130-X)=800X-39 000, 当 X∈[130,150]时,T=500×130=65 000. 所以 800 39000,100 130, 65000,130 150. X X T X (2)由(1)知利润 T 不少于 57 000 元当且仅当 120≤X≤150. 由直方图知需求量 X∈[120,150]的频率为 0.7,所以下一个销售季度内的利润 T 不少于 57 000 元的概率的估计值为 0.7. (3)依题意可得 T 的分布列为 T 45 000 53 000 61 000 65 000 P 0.1 0.2 0.3 0.4 所以 ET=45 000×0.1+53 000×0.2+61 000×0.3+65 000×0.4=59 400. 20. 解:(1)设 A(x1,y1),B(x2,y2),P(x0,y0), 则 2 2 1 1 2 2 =1x y a b , 2 2 2 2 2 2 =1x y a b , 2 1 2 1 = 1y y x x , 由此可得 2 2 1 2 1 2 2 1 2 1 =1b x x y y a y y x x . 因为 x1+x2=2x0,y1+y2=2y0, 0 0 1 2 y x , 所以 a2 =2b2 . 又由题意知,M的右焦点为( 3 ,0),故 a2 -b2 =3. 因此 a2 =6,b2 =3. 所以 M的方程为 2 2 =1 6 3 x y . (2)由 2 2 3 0, 1, 6 3 x y x y 解得 4 3 , 3 3 , 3 x y 或 0, 3. x y 因此|AB|= 4 6 3 . 由题意可设直线 CD 的方程为 y= 5 3 3 3 x n n , 设 C(x3,y3),D(x4,y4). 由 2 2 , 1 6 3 y x n x y 得 3x2 +4nx+2n2 -6=0. 于是 x3,4= 22 2 9 3 n n . 因为直线 CD 的斜率为 1, 所以|CD|= 2 4 3 42 | | 9 3 x x n . 由已知,四边形 ACBD 的面积 21 8 6| | | | 9 2 9 S CD AB n . 当 n=0 时,S 取得最大值,最大值为 8 6 3 . 所以四边形 ACBD 面积的最大值为 8 6 3 . 21. 解:(1)f′(x)= 1ex x m . 由 x=0 是 f(x)的极值点得 f′(0)=0,所以 m=1. 于是 f(x)=e x -ln(x+1),定义域为(-1,+∞),f′(x)= 1e 1 x x . 函数 f′(x)= 1e 1 x x 在(-1,+∞)单调递增,且 f′(0)=0. 因此当 x∈(-1,0)时,f′(x)<0; 当 x∈(0,+∞)时,f′(x)>0. 所以 f(x)在(-1,0)单调递减,在(0,+∞)单调递增. (2)当 m≤2,x∈(-m,+∞)时,ln(x+m)≤ln(x+2),故只需证明当 m=2时,f(x)>0. 当 m=2 时,函数 f′(x)= 1e 2 x x 在(-2,+∞)单调递增. 又 f′(-1)<0,f′(0)>0, 故 f′(x)=0 在(-2,+∞)有唯一实根 x0,且 x0∈(-1,0). 当 x∈(-2,x0)时,f′(x)<0; 当 x∈(x0,+∞)时,f′(x)>0,从而当 x=x0时,f(x)取得最小值. 由 f′(x0)=0 得 0ex = 0 1 2x ,ln(x0+2)=-x0, 故 f(x)≥f(x0)= 0 1 2x +x0= 2 0 0 1 2 x x >0. 综上,当 m≤2 时,f(x)>0. 请考生在第 22、23、24 题中任选择一题作答,如果多做,则按所做的第一题计分,做答时 请写清题号. 22. 解:(1)因为 CD 为△ABC 外接圆的切线, 所以∠DCB=∠A,由题设知 BC DC FA EA , 故△CDB∽△AEF,所以∠DBC=∠EFA. 因为 B,E,F,C 四点共圆, 所以∠CFE=∠DBC, 故∠EFA=∠CFE=90°. 所以∠CBA=90°,因此 CA 是△ABC 外接圆的直径. (2)连结 CE,因为∠CBE=90°,所以过 B,E,F,C 四点的圆的直径为 CE,由 DB=BE,有 CE=DC,又 BC2 =DB·BA=2DB2 ,所以 CA2 =4DB2 +BC2 =6DB2 . 而 DC2=DB·DA=3DB2,故过 B,E,F,C 四点的圆的面积与△ABC 外接圆面积的比值为 1 2 . 23. 解:(1)依题意有 P(2cos α,2sin α),Q(2cos 2α,2sin 2α), 因此 M(cos α+cos 2α,sin α+sin 2α). M的轨迹的参数方程为 cos cos 2 , sin sin 2 x y (α为参数,0<α<2π). (2)M 点到坐标原点的距离 2 2 2 2cosd x y (0<α<2π). 当α=π时,d=0,故 M的轨迹过坐标原点. 24. 解:(1)由 a2+b2≥2ab,b2+c2≥2bc,c2+a2≥2ca, 得 a2 +b2 +c2 ≥ab+bc+ca. 由题设得(a+b+c)2 =1,即 a2 +b2 +c2 +2ab+2bc+2ca=1. 所以 3(ab+bc+ca)≤1,即 ab+bc+ca≤ 1 3 . (2)因为 2 2a b a b , 2 2b c b c , 2 2c a c a , 故 2 2 2 ( )a b c a b c b c a ≥2(a+b+c), 即 2 2 2a b c b c a ≥a+b+c. 所以 2 2 2a b c b c a ≥1. 参考公式: 如果事件 A、B互斥,那么 球的表面积公式 ( ) ( ) ( )P A B P A P B 24S R 如果事件 A、B相互独立,那么 其中 R表示球的半径 ( ) ( ) ( )P A B P A P B 球的体积公式 如果事件 A在一次试验中发生的概率是 p,那么 33 4 V R n次独立重复试验中事件 A恰好发生 k次的概率 其中 R表示球的半径 ( ) (1 ) ( 0,1, 2, )k k n k n nP k C p p k n … 2012年普通高等学校招生全国统一考试 一、 选择题 1、复数 1 3 1 i i = A 2+I B 2-I C 1+2i D 1- 2i 2、已知集合 A={1.3. m },B={1,m} ,A B=A, 则 m= A 0 或 3 B 0 或 3 C 1 或 3 D 1 或 3 3 椭圆的中心在原点,焦距为 4 一条准线为 x=-4 ,则该椭圆的方程为 A 2 16 x + 2 12 y =1 B 2 12 x + 2 8 y =1 C 2 8 x + 2 4 y =1 D 2 12 x + 2 4 y =1 4 已知正四棱柱 ABCD- A1B1C1D1中 ,AB=2,CC1= 2 2 E 为 CC1 的中点,则直线 AC1 与平面 BED 的距离为 A 2 B 3 C 2 D 1 (5)已知等差数列{an}的前 n 项和为 Sn,a5=5,S5=15,则数列 的前 100 项和 为 (A)100 101 (B) 99 101 (C) 99 100 (D) 101 100 (6)△ABC 中,AB 边的高为 CD,若 a·b=0,|a|=1,|b|=2,则 (A) (B) (C) (D) (7)已知α为第二象限角,sinα+sinβ= 3 3 ,则 cos2α= (A) 5- 3 (B) 5- 9 (C) 5 9 (D) 5 3 (8)已知 F1、F2 为双曲线 C:x²-y²=2 的左、右焦点,点 P 在 C 上,|PF1|=|2PF2|,则 cos∠F1PF2= (A) 1 4 (B) 3 5 (C) 3 4 (D) 4 5 (9)已知 x=lnπ,y=log52, 1 2z=e ,则 (A)x<y<z (B)z<x<y (C)z<y<x (D)y<z<x (10) 已知函数 y=x²-3x+c 的图像与 x 恰有两个公共点,则 c= (A)-2 或 2 (B)-9 或 3 (C)-1 或 1 (D)-3 或 1 (11)将字母 a,a,b,b,c,c,排成三行两列,要求每行的字母互不相同,梅列的字母也互不 相同,则不同的排列方法共有 (A)12 种(B)18 种(C)24 种(D)36 种 (12)正方形 ABCD 的边长为 1,点 E 在边 AB 上,点 F 在边 BC 上,AE=BF= 7 3 。 动点 P 从 E 出发沿直线喜爱那个 F 运动,每当碰到正方形的方向的边时反弹,反弹时反 射等于入射角,当点 P 第一次碰到 E 时,P 与正方形的边碰撞的次数为 (A)16(B)14(C)12(D)10 二。填空题:本大题共 4 小题,每小题 5 分,共 20 分,把答案填在题中横线上。 (注意:在试题卷上作答无效) (13)若 x,y 满足约束条件 则 z=3x-y 的最小值为_________。 (14)当函数 取得最大值时,x=___________。 (15)若 的展开式中第 3 项与第 7 项的二项式系数相等,则该展开式中 的系数 为_________。 (16)三菱柱 ABC-A1B1C1 中,底面边长和侧棱长都相等, BAA1=CAA1=50° 则异面直线 AB1 与 BC1 所成角的余弦值为____________。 三.解答题: (17)(本小题满分 10 分)(注意:在试卷上作答无效) △ABC 的内角 A、B、C 的对边分别为 a、b、c,已知 cos(A-C)+cosB=1,a=2c,求 c。 (18)(本小题满分 12 分)(注意:在试题卷上作答无效) 如图,四棱锥 P-ABCD 中,底面 ABCD 为菱形,PA⊥底 面 ABCD,AC=2 2 ,PA=2,E 是 PC 上的一点,PE=2EC. (Ⅰ)证明:PC⊥平面 BED; (Ⅱ)设二面角 A-PB-C 为 90°,求 PD 与平面 PBC 所成 角的大小。 19. (本小题满分 12 分)(注意:在试题卷上作答无效) 乒乓球比赛规则规定:一局比赛,双方比分在 10 平前,一方连续发球 2 次后,对方再 连续发球 2 次,依次轮换。每次发球,胜方得 1 分,负方得 0 分。设在甲、乙的比赛中, 每次发球,发球方得 1 分的概率为 0.6,各次发球的胜负结果相互独立。甲、乙的一局 比赛中,甲先发球。 (Ⅰ)求开始第 4 次发球时,甲、乙的比分为 1 比 2 的概率; (Ⅱ) 表示开始第 4 次发球时乙的得分,求 的期望。 (20)设函数 f(x)=ax+cosx,x∈[0,π]。 (Ⅰ)讨论 f(x)的单调性; (Ⅱ)设 f(x)≤1+sinx,求 a 的取值范围。 21.(本小题满分 12 分)(注意:在试卷上作答无效) 已知抛物线 C:y=(x+1)2 与圆 M:(x-1)2+( 1 2 y )2=r2(r>0)有一个公共点,且在 A 处 两曲线的切线为同一直线 l. (Ⅰ)求 r; (Ⅱ)设 m、n 是异于 l 且与 C 及 M 都相切的两条直线,m、n 的交点为 D,求 D 到 l 的距离。 22(本小题满分 12 分)(注意:在试卷上作答无效........) 函数 f(x)=x2-2x-3,定义数列{xn}如下:x1=2,xn+1 是过两点 P(4,5)、Qn(xn,f(xn))的 直线 PQn与 x 轴交点的横坐标。 (Ⅰ)证明:2 xn<xn+1<3; (Ⅱ)求数列{xn}的通项公式。 2011 年高考数学(全国卷) 一、选择题:本大题共 12 小题,每小题 5分,共 60 分,在每小题给出的四个选项中, 只有一项是满足题目要求的。 1.复数 1z i , z为 z的共轭复数,则 1zz z (A) -2i (B) -i (C) i (D) 2i 2. 函数 2 0y x x 的反函数为 (A) 2 4 xy x R (B) 2 0 4 xy x (C) 24y x x R (D) 24 0y x x 3.下面四个条件中,使a b 成立的充分而不必要的条件是 (A) 1a b (B) 1a b (C) 2 2a b (D) 3 3a b 4.设 nS 为等差数列 na 的前 n项和,若 1 1a ,公差 22, 24k kd S S ,则 k= (A) 8 (B) 7 (C) 6 (D) 5 5.设函数 cos 0f x x ,将 y f x 的图像向右平移 3 个单位长度后,所得的 图像与原图像重合,则的最小值等于 (A) 1 3 (B) 3 (C) 6 (D) 9 6.已知直二面角 l ,点 , ,A AC l C 为垂足, , ,B BD l D 为垂足,若 2, 1AB AC BD ,则 D到平面 ABC 的距离等于 (A) 2 2 (B) 3 3 (C) 6 3 (D) 1 7.某同学有同样的画册 2 本,同样的集邮册 3 本,从中取出 4 本赠送给 4 为朋友,每位 朋友 1 本,则不同的赠送方法共有 (A) 4 种 (B) 10 种 (C) 18 种 (D) 20 种 8.曲线 2 1xy e 在点 0,2 处的切线与直线 0y 和 y x 围成的三角形的面积为 (A) 1 3 (B) 1 2 (C) 2 3 (D) 1 9.设 f x 是周期为 2的奇函数,当0 1x 时, 2 1f x x x ,则 5 2 f (A) 1 2 (B) 1 4 (C) 1 4 (D) 1 2 10.已知抛物线C: 2 4y x 的焦点为F,直线 2 4y x 与C交于A、B两点,则cos AFB (A) 4 5 (B) 3 5 (C) 3 5 (D) 4 5 11.已知平面 截一球面得圆 M,过圆心 M且与 成60二面角的平面 截该球面得圆 N, 脱该球面的半径为 4.圆 M 的面积为4 ,则圆 N的面积为 (A) 7 (B) 9 (C) 11 (D) 13 12. 设向量 , ,a b c 满足 11, , , 60 2 a b a b a c b c ,则 c 的最大值对于 (A) 2 (B) 3 (C) 2 (D) 1 二、填空题:本大题共 4小题,每小题 5 分,共 20 分.请将答案填在答题卡对应题号的 位置上,一题两空的题,其答案按先后次序填写. 13. 20 1 x 的二项展开式中, x的系数与 9x 的系数之差为 . 14. 已知 , 2 , 5sin 5 ,则 tan 2 . 15. 已知 1 2F F、 分别为双曲线 2 2 : 1 9 27 x yC 的左、右焦点,点 A C ,点 M 的坐标为 2,0 ,AM 为 1 2F AF 的角平分线,则 2AF . 16. 已知点 E、F 分别在正方体 1 1 1 1ABCD ABC D 的棱 1 1BB CC、 上,且 1 2B E EB , 12CF FC ,则面 AEF 与面 ABC 所成的二面角的正切值等于 . 三、解答题:本大题共 6小题,共 70 分。解答应写出文字说明、证明过程或演算步骤。 17.(本小题满分 10 分) ABC 的内角 A、B、C的对边分别为 , ,a b c。已知 90 , 2A C a c b ,求 C 18.(本小题满分 12 分) 根据以往统计资料,某地车主购买甲种保险的概率为 0.5,购买乙种保险但不购买 甲种保险的概率为 0.3,设各车主购买保险相互独立。 (Ⅰ)求该地 1 为车主至少购买甲、乙两种保险中的 1 种的概率; (Ⅱ)X 表示该地的 100 为车主中,甲、乙两种保险都不购买的车主数,求 X 的期 望。 19.(本小题满分 12 分) 如图,四棱锥 S-ABCD 中, / / ,AB CD BC CD ,侧面 SAB 为等边三角形, AB=BC=2,CD=SD=1. (Ⅰ)证明: SD SAB平面 ; (Ⅱ)求 AB 与平面 SBC 所成的角的大小。 20.(本小题满分 12 分) 设数列 na 满足 1 1 1 10, 1 1 1n n a a a (Ⅰ)求 na 的通项公式; (Ⅱ)设 11 n n a b n ,记 1 n n k k S b ,证明: 1nS 。 21.(本小题满分 12 分) 已知 O 为坐标原点,F 为椭圆 2 2: 1 2 yC x 在 y 轴正半轴上的焦点,过 F 且斜率 为 2 的 直 线 l 与 C 交 于 A 、 B 两 点 , 点 P 满 足 0.OA OB OP (Ⅰ)证明:点 P 在 C 上; (Ⅱ)设点 P 关于点 O 的对称点为 Q,证明:A、P、B、 Q 四点在同一个圆上。 22.(本小题满分 12 分) (Ⅰ)设函数 2ln 1 2 xf x x x ,证明:当 0x 时, 0f x (Ⅱ)从编号 1 到 100 的 100 张卡片中每次随机抽取一张,然后放回,用这种方式 连续抽取 20 次,设抽到的 20 个号码互不相同的概率为 p,证明: 19 2 9 1 10 p e 2010 年普通高等学校招生全国统一考试 一.选择题 (1)复数 3 2 2 3 i i (A)i (B) i (C)12-13 i (D) 12+13 i (2)记 cos( 80 ) k ,那么 tan100 A. 21 k k B. - 21 k k C. 21 k k D. - 21 k k (3)若变量 ,x y满足约束条件 1, 0, 2 0, y x y x y 则 2z x y 的最大值为 (A)4 (B)3 (C)2 (D)1 (4)已知各项均为正数的等比数列{ na }, 1 2 3a a a =5, 7 8 9a a a =10,则 4 5 6a a a = (A) 5 2 (B) 7 (C) 6 (D) 4 2 (5) 3 53(1 2 ) (1 )x x 的展开式中 x 的系数是 (A) -4 (B) -2 (C) 2 (D) 4 (6)某校开设 A类选修课 3 门,B 类选择课 4门,一位同学从中共选 3 门,若要求两类课程中各至少选一门,则不同的选法共有 (A) 30 种 (B)35 种 (C)42 种 (D)48 种 (7)正方体 ABCD- 1 1 1 1A BC D 中,B 1B与平面 AC 1D 所成角的余弦值为 A 2 3 B 3 3 C 2 3 D 6 3 (8)设 a= 3log 2,b=In2,c= 1 25 ,则 A a查看更多