- 2021-05-13 发布 |
- 37.5 KB |
- 18页
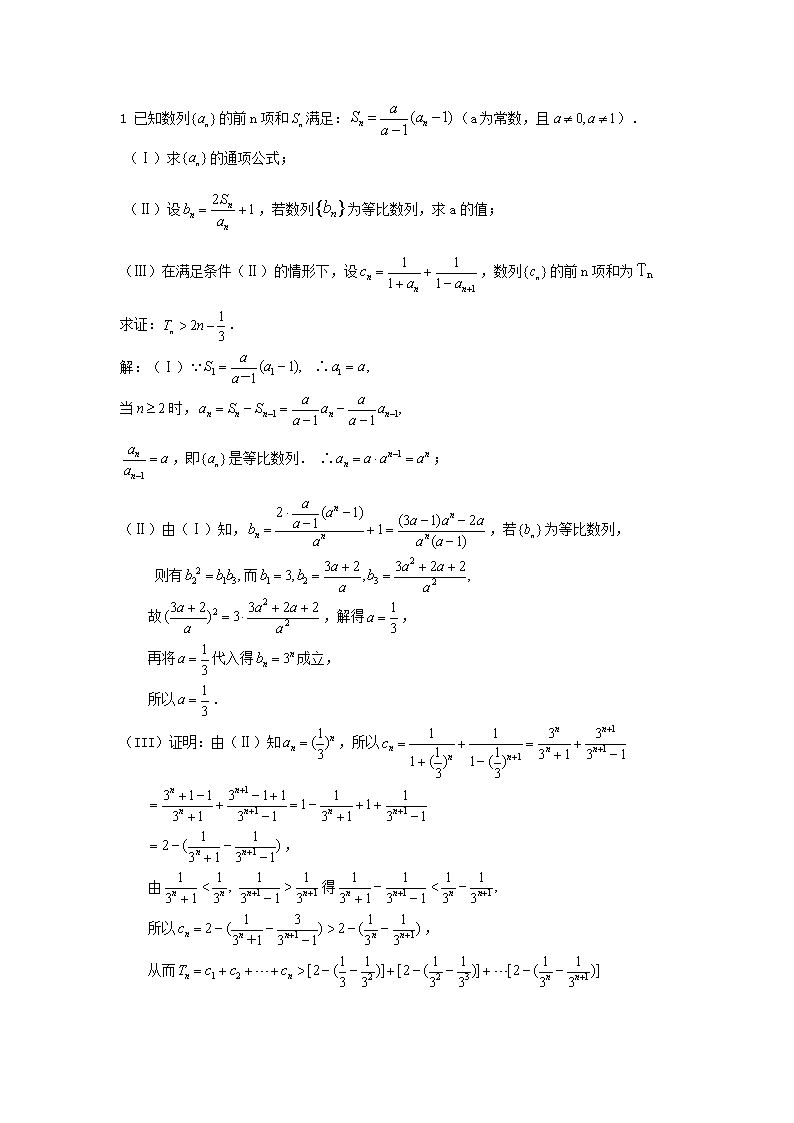


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高考数学第二轮复习数列典型例题
1 已知数列的前n项和满足:(a为常数,且). (Ⅰ)求的通项公式; (Ⅱ)设,若数列为等比数列,求a的值; (Ⅲ)在满足条件(Ⅱ)的情形下,设,数列的前n项和为Tn 求证:. 解:(Ⅰ)∴ 当时, ,即是等比数列. ∴; (Ⅱ)由(Ⅰ)知,,若为等比数列, 则有而 故,解得, 再将代入得成立, 所以. (III)证明:由(Ⅱ)知,所以 , 由得 所以, 从而 . 即. 2 数列中,,(是常数,),且成公比不为的等比数列。 (I)求的值; (II)求的通项公式。 解:(I),,,因为,,成等比数列, 所以,解得或. 当时,,不符合题意舍去,故. (II)当时,由于,, ,所以。 又,,故.当n=1时,上式也成立,所以 3 已知数列中, (1)求证:数列与都是等比数列;(2)求数列前的和; (3)若数列前的和为,不等式对恒成立,求的最大值。 解:(1)∵,∴ ∴数列是以1为首项,为公比的等比数列; 数列是以为首项,为公比的等比数列。 (2) (3) 当且仅当时取等号,所以,即,∴的最大值为-48 4 已知等差数列的公差大于0,且是方程的两根,数列的前n项的和为,且. (1) 求数列,的通项公式; (2) 记,求证:. 解:(Ⅰ)∵a3,a5是方程的两根,且数列的公差d>0, ∴a3=5,a5=9,公差 ∴ 又当n=1时,有b1=S1=1- 当 ∴数列{bn}是等比数列, ∴ (Ⅱ)由(Ⅰ)知 ∴ ∴ 5 已知数列的前项和为,对一切正整数,点都在函数的图像上,且过点的切线的斜率为. (1)求数列的通项公式. (2)若,求数列的前项和. (3)设,等差数列的任一项,其中是中的最小数,,求的通项公式. 解:(1)点都在函数的图像上,, 当时, 当n=1时,满足上式,所以数列的通项公式为 (2)由求导可得 过点的切线的斜率为,. . ① 由①×4,得 ② ①-②得: (3),. 又,其中是中的最小数,. 是公差是4的倍数,. 又,,解得m=27. 所以, 设等差数列的公差为,则 ,所以的通项公式为 6 已知是数列的前项和,,且,其中. (1)求数列的通项公式; (2)求 . 解:① 又也满足上式,() 数列是公比为2,首项为的等比数列 ② ② 7 函数对任意x∈R都有f(x)+f(1-x)=. (1)求的值; (2)数列的通项公式。 (3)令试比较Tn与Sn的大小。 解:(1)令 令 (2) 又,两式相加 是等差数列 (3) 8、已知数列中,其前n项和为 满足. (1)试求数列的通项公式. (2)令是数列的前n项和,证明:. (3)证明:对任意的,均存在,使得(2)中的成立. 解:(1)由得 ,,即 又, 故数列的通项公式为. (2) (3)证明:由(2)可知 若,则得,化简得 , 当,即 当,即 ,取即可, 综上可知,对任意的均存在使得时(2)中的成立 9 已知数列{an}的前n项和为Sn,并且满足a1=2,nan+1=Sn+n(n+1). (1)求数列; (2)设 解:(1) (2) 10 已知二次函数f(x)=ax2+bx+c的图象顶点坐标是(,-),且f(3)=2 (1)求y=f(x)的表达式,并求出f(1),f(2)的值; (2)数列,若对任意的实数,其中是定义在实数集R上的一个函数,求数列的通项公式; 解:(1) (2)令 11 已知数列{an}满足a1=5,a2=5,an+1=an+6an-1(n≥2且n∈N*) (1)求出所有使数列值,并说明理由; (2)求数列的通项公式; (3)求证: 解:(1) (2) (3)当时, 12 已知数列,满足,数列的前项和为. (Ⅰ)求数列的通项公式; (Ⅱ)求证:; (Ⅲ)求证:当时,. 解:(1)由,得,代入,得, 整理,得,从而有,, 是首项为1,公差为1的等差数列,即. (2), , , , . (3),. 由(2)知,, . 13 已知数列的首项,前项和为,且、、分别是直线上的点A、B、C的横坐标,点B分所成的比为,设 。 ⑴ 判断数列是否为等比数列,并证明你的结论; ⑵ 设,证明:。 ⑴由题意得 数列是以为首项,以2为公比的等比数列。 [则()] ⑵由及得 则 14 已知各项均为正数的数列满足且是、的等差中项 (1)求数列的通项公式; (2)若,求使成立的正整数的最小值。 解: 数列的各项均为正数,, 即 数列是以2为公比的等比数列。 是的等差中项, 数列的通项公式为 (2)由(1)及,得,(6分) ① ② ②-①得, 要使成立,只需成立,即 成立的正整数n的最小值为5。 15 已知,且,数列的前项和为,它满足条件.数列中,。 (1)求数列的前项和; (2)若对一切都有,求的取值范围。 解:(1) 当时,. 当≥2时,=, 此时·=·, ……= 设……+, ……+, (2)由可得 当时,由 可得, 对一切都成立,此时的解为. 当时,由 可得 ≥ 对一切都成立, 此时的解为. 由,可知,对一切都有的的取值范围是或. 16 设数列的前n项和为Sn=2n2,为等比数列,且 (1)求数列和的通项公式; (2)设,求数列的前n项和。 解:(1):当 故{an}的通项公式为的等差数列. 设{bn}的通项公式为 故 (2) 两式相减得 17 设不等式所表示的平面区域为,记内的格点(,)(、∈z)的个数为(∈). (Ⅰ) 求,的值及的表达式; (Ⅱ)记,若对于任意∈,总有≤m成立,求实数m的取值范围; (Ⅲ) 设为数列{}的前项和,其中=,问是否存在正整数、t,使 <成立?若存在,求出正整数,t;若不存在,请说明理由. 解:(Ⅰ)=3,=6. 由>0,0<≤,得0<<3,又∈,∴=1,或=2. 当=1,0<≤2时,共有2个格点; 当=2,0<≤时,共有个格点. 故 . (Ⅱ)由(1)知=,则-=. ∴当≥3时,<. 又=9<==,所以≤,故≥. (Ⅲ)假设存在满足题意的和, 由(1)知==,故. 则<. 变形得<,即<0. ∴1<(8-)<15. 由于、均为正整数,所以==1. 附:, . 当时, 由,得,. 当时, ,由,得,不存在. 所以==1. 18 已知二次函数的图像经过坐标原点,其导函数为数列{}的前n项和为,点均在函数的图像上. (I)求数列{}的通项公式; (II)设,的前n项和,求使得对所有都成立的最小正整数m. 解:(I)设这二次函数, 由于,得 又因为点的图像上, 所以 当 (II)由(I)得知 故 因此,要使,必须且仅须满足 即, 所以满足要求的最小正整数m为10。 19 数列,由下列条件确定:①a1<0,b 1<0.②当k≥2时,ak和bk满足下列条件:当. (1)若,,分别写出{an}、{bn}的前四项. (2)证明数列{ak-bk}是等比数列. (3)设是满足b1>b2>…>bn的最大整数时,用a1、b1表示n满足的条件. 解:(1) (2)当时, 当时, 又,∴数列是等比数列. (3)当b1>b2>…>bn(n≥2)时,bk≠bk-1(2≤k≤n). 由(2)知:不成立,. 从而对于2≤k≤n有ak=ak-1,bk= 于是 若,则 这与是满足b1>b2>…>bn(n≥2)的最大整数矛盾. ∴n是满足的最小整数. n是满足大于的最小整数 20 已知函数的定义域为,且同时满足:对任意,总有,; 若,且,则有. (1)求的值; (2)试求的最大值; (3)设数列的前项和为,且满足, 求证:. 解:(1)令,则,又由题意,有 (2)任取 且,则0< 的最大值为 (3)由 又由 数列为首项为1,公比为的等比数列, 当时,,不等式成立, 当时, , 不等式成立 假设时,不等式成立。 即 则 当时, 即 时,不等式成立 故 对 ,原不等式成立。 17 已知数列的前n项和为且,数列满足且. (1)求的通项公式; (2)求证:数列为等比数列; (3)求前n项和的最小值. 解: (1)由得, ∴ (2)∵,∴, ∴; ∴由上面两式得,又 ∴数列是以-30为首项,为公比的等比数列. (3)由(2)得,∴ = ,∴是递增数列 当n=1时, <0;当n=2时, <0;当n=3时, <0;当n=4时, >0,所以,从第4项起的各项均大于0,故前3项之和最小. 且 查看更多