- 2021-05-13 发布 |
- 37.5 KB |
- 13页


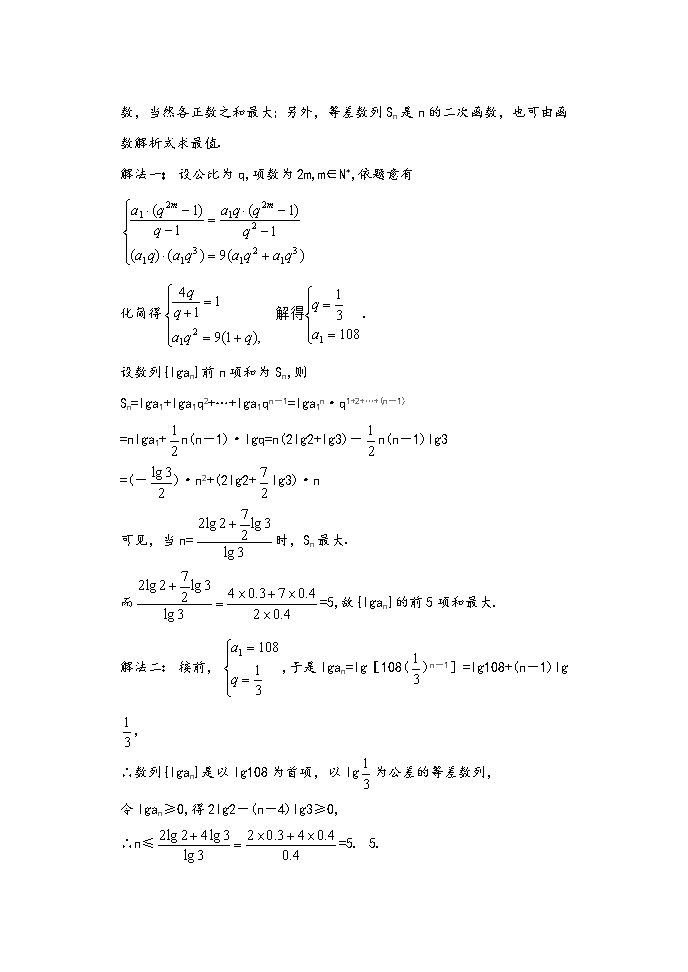
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高考数列命题热点研讨3
第三讲:2013年高考数列命题热点研讨(3) 主讲人:孟老师 第四部分:数列2013年考题大预测 列作为高考的必考点之一,也是高考的重点和热点.数列题目占的分值约为17分,一般是一个小题和一个大题.是2013年新课标高考的一个必考的内容.根据往年的试题,我预测,高考仍然会是稳中求变的考察.小题仍然以基础为主,主要考察通项公式、前n项和等内容.大题主要是考察函数与方程思想、转化与化归思想、化简、求解能力、数学归纳法、求和的几种方法为重点.但是近几年北京和安徽等省市都把数列设置成了压轴的大题,这是一种新的命题趋势,是我们大家值得注意的.数列题若是作为压轴题来出,难度是相当的大的,希望同学们有心理准备.不过要是平时复习好了,也没有什么怕的. 孟老师大胆预测1:等差数列 等差数列是高考的必考点,这个不用我做预测,大家都知道要出,但是出什么题型,怎么出,我们就不得而知了.这里本人试着小小的预测一下,看2013年高考是否能出到本人预测的题目所考察的店.我们要注意等差数列的对称性等问题,要会求通项和前n项和. 预测例题1(2012年重庆高考) 在等差数列中,则的前5项和= A.7 B.15 C.20 D.25 【答案】B 孟老师大胆预测2:等比数列 等比数列也是高考的一个命题点,考察的内容和方式和等差数列基本上一样.我们要注意基本公式的运用和基本公式经过变形后的运用.当然基本公式变形的运用是为了我们简化计算过程的,要是不会用变形,我们在计算的时候可能就要花费一些力气了.小题难度比较下,大题难度一般为中等. 预测例题2 设等比数列{an}的各项均为正数,项数是偶数,它的所有项的和等于偶数项和的4倍,且第二项与第四项的积是第3项与第4项和的9倍,问数列{lgan}的前多少项和最大?(lg2=0 3,lg3=0 4) 解:命题意图 本题主要考查等比数列的基本性质与对数运算法则,等差数列与等比数列之间的联系以及运算、分析能力 知识依托 本题须利用等比数列通项公式、前n项和公式合理转化条件,求出an;进而利用对数的运算性质明确数列{lgan}为等差数列,分析该数列项的分布规律从而得解 错解分析 题设条件中既有和的关系,又有项的关系,条件的正确转化是关键,计算易出错;而对数的运算性质也是易混淆的地方 技巧与方法 突破本题的关键在于明确等比数列各项的对数构成等差数列,而等差数列中前n 项和有最大值,一定是该数列中前面是正数,后面是负数,当然各正数之和最大;另外,等差数列Sn是n的二次函数,也可由函数解析式求最值 解法一 设公比为q,项数为2m,m∈N*,依题意有 化简得 设数列{lgan}前n项和为Sn,则 Sn=lga1+lga1q2+…+lga1qn-1=lga1n·q1+2+…+(n-1) =nlga1+n(n-1)·lgq=n(2lg2+lg3)-n(n-1)lg3 =(-)·n2+(2lg2+lg3)·n 可见,当n=时,Sn最大 而=5,故{lgan}的前5项和最大 解法二 接前,,于是lgan=lg[108()n-1]=lg108+(n-1)lg, ∴数列{lgan}是以lg108为首项,以lg为公差的等差数列, 令lgan≥0,得2lg2-(n-4)lg3≥0, ∴n≤=5 5 由于n∈N*,可见数列{lgan}的前5项和最大 孟老师大胆预测3:数列的综合 高考试卷中若是数列作为压轴题出现,那么对数列的要求就会比较高.数列会和对数、三角函数、导数甚至会和二项式结合出来命题,这是值得我们大家注意的.我们要非常熟悉数列的求和方法:分组求和法、倒序相加法、错位相减法、裂项求和法、累加法、相乘相消法等方法. 预测例题3(2011年全国卷) (本小题满分12分)(注意:在试题卷上作答无效) 设数列满足且 (Ⅰ)求的通项公式; (Ⅱ)设 解:(I)由题设 即是公差为1的等差数 列. 又 所以 (II)由(I)得 热点预测 1(2011年四川) 数列的首项为, 为等差数列且 .若则,,则 (A)0 (B)3 (C)8 (D)11 答案:B解析:由已知知由叠加法 2(2011年湖南高考) 设是等差数列的前项和,且,则 答案:25解析:由可得,所以. 3(2012北京高考) 已知等差数列为其前n项和.若,,则=_______. 【解析】因为 , 所以,. 【答案】, 4(2012辽宁高考) 在等差数列{an}中,已知a4+a8=16,则该数列前11项和S11= (A)58 (B)88 (C)143 (D)176 【答案】B 【解析】在等差数列中, ,答案为B 【点评】本题主要考查等差数列的通项公式、性质及其前n项和公式,同时考查运算求解能力,属于中档题.解答时利用等差数列的性质快速又准确. 5(2012安徽卷) 公比为2的等比数列{} 的各项都是正数,且 =16,则= (A) 1 (B)2 (C) 4 (D)8 【解析】选 6(2010年天津高考)(本小题满分14分) 在数列中,,且对任意.,,成等差数列,其公差为. (Ⅰ)若=,证明,,成等比数列() (Ⅱ)若对任意,,,成等比数列,其公比为. 本小题主要考查等差数列的定义及通项公式,前n项和公式、等比数列的定义、数列求和等基础知识,考查运算能力、推理论证能力、综合分析和解决问题的能力及分类讨论的思想方法.满分14分. (Ⅰ)证明:由题设,可得. 所以 ==2k(k+1) 由=0,得 于是. 所以成等比数列. (Ⅱ)证法一:(i)证明:由成等差数列,及 成等比数列,得 当≠1时,可知≠1,k 从而 所以是等差数列,公差为1. (Ⅱ)证明:,,可得,从而=1.由(Ⅰ)有 所以 因此, 以下分两种情况进行讨论: (1) 偶数时,设n=2m() 若m=1,则. 若m≥2,则 + 所以 (2)当n为奇数时,设n=2m+1() 所以从而··· 综合(1)(2)可知,对任意,,有 证法二:(i)证明:由题设,可得 所以 由可知.可得, 所以是等差数列,公差为1. (ii)证明:因为所以. 所以,从而,.于是,由(i)可知所以是公差为1的等差数列.由等差数列的通项公式可得= ,故. 从而. 所以,由,可得 . 于是,由(i)可知 以下同证法一. 7(2010年全国新课标卷)(本小题满分12分) 设数列满足 (1)的通项公式; (2)求数列的前n项和 解:(Ⅰ)由已知,当n≥1时, .而 所以数列{}的通项公式为. (Ⅱ)由知 ① 从而 ② ①-②得 . 即 8(2011年广东高考) 设b>0,数列满足a1=b,. (I)求数列的通项公式;(II)证明:对于一切正整数n, 解(1)法一:,得 , 设,则, (ⅰ)当时,是以为首项,为公差的等差数列, 即,∴ (ⅱ)当时,设,则, 令,得, , 知是等比数列,,又, ,. 法二:(ⅰ)当时,是以为首项,为公差的等差数列, 即,∴ (ⅱ)当时,,, , 猜想,下面用数学归纳法证明: ①当时,猜想显然成立;②假设当时,,则 , 所以当时,猜想成立, 由①②知,,. (2)(ⅰ)当时, ,故时,命题成立; (ⅱ)当时,, , ,以上n个式子相加, .故当时,命题成立;综上(ⅰ)(ⅱ)知命题成立.查看更多