全国各地高考文科数学试题分类汇编7立体几何

全国各地高考文科数学试题分类汇编7立体几何

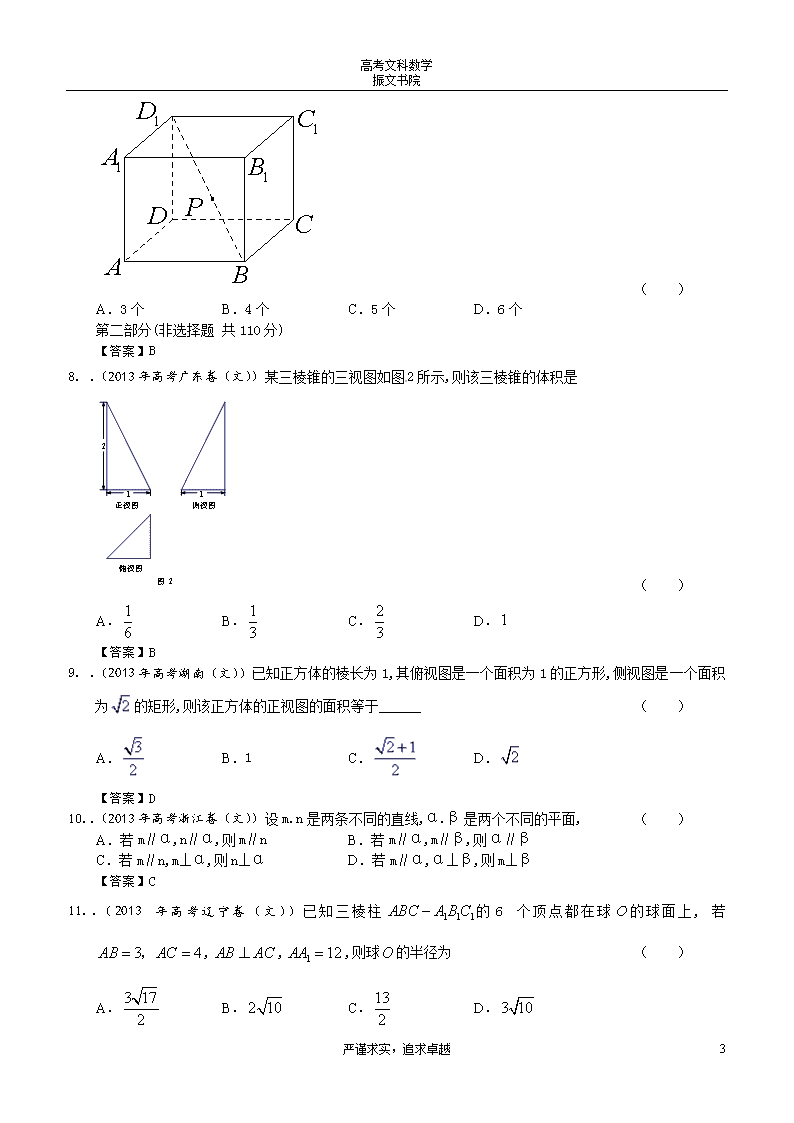
高考文科数学 振文书院 ‎2013年全国各地高考文科数学试题分类汇编7：立体几何 ‎ ‎ 一、选择题 ．（2013年高考重庆卷（文））某几何体的三视图如题(8)所示,则该几何体的表面积为 ‎ （　　）‎ A． B． C． D．‎ ‎【答案】D ‎ ．（2013年高考课标Ⅱ卷（文））一个四面体的顶点在空间直角坐标系中的坐标分别是,画该四面体三视图中的正视图时,以平面为投影面,则得到正视图可以为 ‎ ‎ （　　）‎ A． B． C． D．‎ ‎【答案】A ‎ ．（2013年高考课标Ⅰ卷（文））某几何函数的三视图如图所示,则该几何的体积为 ‎ ‎ （　　）‎ A． B． C． D．‎ 24‎ 严谨求实，追求卓越 高考文科数学 振文书院 ‎【答案】A ．（2013年高考大纲卷（文））已知正四棱锥的正弦值等于 （　　）‎ A． B． C． D．‎ ‎【答案】A ‎ ．（2013年高考四川卷（文））一个几何体的三视图如图所示,则该几何体可以是 （　　）‎ A．棱柱 B．棱台 C．圆柱 D．圆台 ‎【答案】D ‎ ．（2013年高考浙江卷（文））已知某几何体的三视图(单位:cm)如图所示,则该几何体的体积是 ‎ （　　）‎ A．108cm3 B．100 cm3 C．92cm3 D．84cm3‎ ‎【答案】B ‎ ．（2013年高考北京卷（文））如图,在正方体中,为对角线的三等分点,则到各顶点的距离的不同取值有 ‎ 24‎ 严谨求实，追求卓越 高考文科数学 振文书院 ‎ （　　）‎ A．3个 B．4个 C．5个 D．6个 第二部分(非选择题 共110分)‎ ‎【答案】B ‎ ．（2013年高考广东卷（文））某三棱锥的三视图如图2所示,则该三棱锥的体积是 ‎ （　　）‎ A． B． C． D．‎ ‎【答案】B ‎ ．（2013年高考湖南（文））已知正方体的棱长为1,其俯视图是一个面积为1的正方形,侧视图是一个面积为的矩形,则该正方体的正视图的面积等于______ （　　）‎ A． B．1 C． D．‎ ‎【答案】D ‎ ．（2013年高考浙江卷（文））设m.n是两条不同的直线,α.β是两个不同的平面, （　　）‎ A．若m∥α,n∥α,则m∥n B．若m∥α,m∥β,则α∥β ‎ C．若m∥n,m⊥α,则n⊥α D．若m∥α,α⊥β,则m⊥β ‎【答案】C ‎ ．（2013年高考辽宁卷（文））已知三棱柱的6个顶点都在球的球面上,若,,,则球的半径为 （　　）‎ A． B． C． D． ‎ 24‎ 严谨求实，追求卓越 高考文科数学 振文书院 ‎【答案】C ‎ ．（2013年高考广东卷（文））设为直线,是两个不同的平面,下列命题中正确的是 （　　）‎ A．若,,则 B．若,,则 ‎ C．若,,则 D．若,,则 ‎【答案】B ‎ ．（2013年高考山东卷（文））一个四棱锥的侧棱长都相等,底面是正方形,其正(主)视图如右图所示该四棱锥侧面积和体积分别是 ‎ （　　）‎ A． B． C． D．8,8‎ ‎【答案】B ‎ ．（2013年高考江西卷（文））一几何体的三视图如右所示,则该几何体的体积为 ‎ （　　）‎ A．200+9π B．200+18π C．140+9π D．140+18π ‎ ‎【答案】A ‎ 二、填空题 ．（2013年高考课标Ⅱ卷（文））已知正四棱锥O-ABCD的体积为,底面边长为,则以O为球心,OA为半径的球的表面积为________.‎ ‎【答案】 ‎ ．（2013年高考湖北卷（文））我国古代数学名著《数书九章》中有“天池盆测雨”题:在下雨时,用一个圆台形的天池盆接雨水. 天池盆盆口直径为二尺八寸,盆底直径为一尺二寸,盆深一尺八寸. 若 24‎ 严谨求实，追求卓越 高考文科数学 振文书院 盆中积水深九寸,则平地降雨量是__________寸. ‎ ‎(注:①平地降雨量等于盆中积水体积除以盆口面积;②一尺等于十寸)‎ ‎【答案】3 ‎ ．（2013年高考课标Ⅰ卷（文））已知是球的直径上一点,,平面,为垂足,截球所得截面的面积为,则球的表面积为_______.‎ ‎【答案】; ‎ ．（2013年高考北京卷（文））某四棱锥的三视图如图所示,该四棱锥的体积为__________.‎ ‎1‎ 俯视图 侧（左）视图 正（主）视图 ‎ 2 1 1 2 ‎ ‎【答案】3‎ ．（2013年高考陕西卷（文））某几何体的三视图如图所示, 则其表面积为________. ‎ ‎【答案】 ‎ ．（2013年高考大纲卷（文））已知圆和圆是球的大圆和小圆,其公共弦长等于球的半径,则球的表面积等于______.‎ ‎【答案】 ‎ ．（2013年上海高考数学试题（文科））已知圆柱的母线长为,底面半径为,是上地面圆心,、是下底面圆周上两个不同的点,是母线,如图.若直线与所成角的大小为,则________.‎ ‎【答案】 ‎ ．（2013年高考天津卷（文））已知一个正方体的所有顶点在一个球面上. 若球的体积为, 则正方体的棱长为 ______.‎ ‎【答案】 ‎ ．（2013年高考辽宁卷（文））某几何体的三视图如图所示,则该几何体的体积是____________.‎ 24‎ 严谨求实，追求卓越 高考文科数学 振文书院 ‎【答案】 ‎ ．（2013年高考江西卷（文））如图,正方体的底面与正四面体的底面在同一平面α上,且AB//CD,则直线EF与正方体的六个面所在的平面相交的平面个数为_____________.‎ ‎【答案】4 ‎ ．（2013年高考安徽（文））如图,正方体的棱长为1,为的中点,为线段上的动点,过点的平面截该正方体所得的截面记为,则下列命题正确的是__________(写出所有正确命题的编号).‎ ‎①当时,为四边形;②当时,为等腰梯形;③当时,与的交点满足;④当时,为六边形;⑤当时,的面积为.‎ ‎【答案】①②③⑤ ‎ 三、解答题 ．（2013年高考辽宁卷（文））如图,‎ 24‎ 严谨求实，追求卓越 高考文科数学 振文书院 ‎(I)求证:‎ ‎(II)设 ‎【答案】‎ ‎ ‎ ‎ ‎ ．（2013年高考浙江卷（文））如图,在在四棱锥P-ABCD中,PA⊥面ABCD,AB=BC=2,AD=CD=,PA=,∠ABC=120°,G为线段PC上的点.‎ ‎(Ⅰ)证明:BD⊥面PAC ; ‎ ‎(Ⅱ)若G是PC的中点,求DG与APC所成的角的正切值;‎ ‎(Ⅲ)若G满足PC⊥面BGD,求 的值.‎ 24‎ 严谨求实，追求卓越 高考文科数学 振文书院 ‎【答案】解:证明:(Ⅰ)由已知得三角形是等腰三角形,且底角等于30°,且,所以;、,又因为; ‎ ‎(Ⅱ)设,由(1)知,连接,所以与面所成的角是,由已知及(1)知:, ,所以与面所成的角的正切值是; ‎ ‎(Ⅲ)由已知得到:,因为,在中,,设 ‎ ‎ ‎ 24‎ 严谨求实，追求卓越 高考文科数学 振文书院 ．（2013年高考陕西卷（文））如图, 四棱柱ABCD-A1B1C1D1的底面ABCD是正方形, O为底面中心, A1O⊥平面ABCD, . ‎ ‎(Ⅰ) 证明: A1BD // 平面CD1B1; ‎ ‎(Ⅱ) 求三棱柱ABD-A1B1D1的体积. ‎ ‎【答案】解: (Ⅰ) 设. ‎ ‎. ‎ ‎ ‎ ‎.(证毕) ‎ ‎(Ⅱ) . ‎ 在正方形AB CD中,AO = 1 . ‎ ‎. ‎ 所以,. ‎ ．（2013年高考福建卷（文））如图,在四棱锥中,,,,,,,.‎ ‎(1)当正视图方向与向量的方向相同时,画出四棱锥的正视图.(要求标出尺寸,并画出演算过程);‎ ‎(2)若为的中点,求证:;‎ ‎(3)求三棱锥的体积.‎ 24‎ 严谨求实，追求卓越 高考文科数学 振文书院 ‎【答案】解法一:(Ⅰ)在梯形中,过点作,垂足为, ‎ 由已知得,四边形为矩形, ‎ 在中,由,,依勾股定理得: ‎ ‎,从而 ‎ 又由平面得, ‎ 从而在中,由,,得 ‎ 正视图如右图所示: ‎ ‎(Ⅱ)取中点,连结, ‎ 在中,是中点, ‎ ‎∴,,又, ‎ ‎∴, ‎ ‎∴四边形为平行四边形,∴ ‎ 又平面,平面 ‎ ‎∴平面 ‎ ‎(Ⅲ) ‎ 又,,所以 ‎ 解法二: ‎ ‎(Ⅰ)同解法一 ‎ ‎(Ⅱ)取的中点,连结, ‎ 在梯形中,,且 ‎ ‎∴四边形为平行四边形 ‎ ‎∴,又平面,平面 ‎ ‎∴平面,又在中, ‎ 平面,平面 ‎ ‎∴平面.又, ‎ ‎∴平面平面,又平面 ‎ ‎∴平面 ‎ ‎(Ⅲ)同解法一 ‎ ．（2013年高考广东卷（文））如图4,在边长为1的等边三角形中,分别是边上的点,,是的中点,与交于点,将沿折起,得到如图5所示的三棱锥,其中.‎ 24‎ 严谨求实，追求卓越 高考文科数学 振文书院 ‎(1) 证明://平面;‎ ‎(2) 证明:平面;‎ ‎(3) 当时,求三棱锥的体积.‎ ‎ ‎ ‎【答案】(1)在等边三角形中, ‎ ‎,在折叠后的三棱锥中 ‎ 也成立, ,平面, ‎ 平面,平面; ‎ ‎(2)在等边三角形中,是的中点,所以①,. ‎ ‎ 在三棱锥中,,② ‎ ‎; ‎ ‎(3)由(1)可知,结合(2)可得. ‎ ‎ ‎ ．（2013年高考湖南（文））如图2.在直菱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=,AA1=3,D是BC的中点,点E在菱BB1上运动.‎ ‎(I) 证明:AD⊥C1E;‎ ‎(II) 当异面直线AC,C1E 所成的角为60°时,求三菱子C1-A2B1E的体积.‎ 24‎ 严谨求实，追求卓越 高考文科数学 振文书院 ‎【答案】解: (Ⅰ) . ‎ ‎ ‎ ‎. ‎ ‎(证毕) ‎ ‎(Ⅱ). ‎ ‎. ‎ ．（2013年高考北京卷（文））如图,在四棱锥中,,,,平面底面,,和分别是和的中点,求证:‎ ‎(1)底面;(2)平面;(3)平面平面 ‎【答案】(I)因为平面PAD⊥平面ABCD,且PA垂直于这个平面的交线AD ‎ 所以PA垂直底面ABCD. ‎ ‎(II)因为AB∥CD,CD=2AB,E为CD的中点 ‎ 所以AB∥DE,且AB=DE ‎ 所以ABED为平行四边形, ‎ 所以BE∥AD,又因为BE平面PAD,AD平面PAD ‎ 所以BE∥平面PAD. ‎ ‎(III)因为AB⊥AD,而且ABED为平行四边形 ‎ 所以BE⊥CD,AD⊥CD,由(I)知PA⊥底面ABCD, ‎ 所以PA⊥CD,所以CD⊥平面PAD ‎ 所以CD⊥PD,因为E和F分别是CD和PC的中点 ‎ 所以PD∥EF,所以CD⊥EF,所以CD⊥平面BEF,所以平面BEF⊥平面PCD. ‎ 24‎ 严谨求实，追求卓越 高考文科数学 振文书院 ‎ ‎ ．（2013年高考课标Ⅰ卷（文））如图,三棱柱中,,,.‎ ‎(Ⅰ)证明:;‎ ‎(Ⅱ)若,,求三棱柱的体积.‎ ‎【答案】【答案】(I)取AB的中点O,连接、、,因为CA=CB,所以,由于AB=A A1,∠BA A1=600,故为等边三角形,所以OA⊥AB. ‎ ‎ ‎ 因为OC⨅OA=O,所以AB平面OAC.又ACC平面OAC,故ABAC. ‎ ‎(II)由题设知 ‎ ‎ ‎ ‎ ‎ ．（2013年高考山东卷（文））如图,四棱锥中,,,‎ 24‎ 严谨求实，追求卓越 高考文科数学 振文书院 分别为 的中点 ‎(Ⅰ)求证:;(Ⅱ)求证:‎ ‎【答案】‎ ‎ ‎ ‎ ‎ 24‎ 严谨求实，追求卓越 高考文科数学 振文书院 ‎ ‎ ‎ ‎ ．（2013年高考四川卷（文））‎ 如图,在三棱柱中,侧棱底面,,,分别是线段的中点,是线段上异于端点的点.‎ ‎(Ⅰ)在平面内,试作出过点与平面平行的直线,说明理由,并证明直线平面;‎ ‎(Ⅱ)设(Ⅰ)中的直线交于点,求三棱锥的体积.(锥体体积公式:,其中为底面面积,为高)‎ 24‎ 严谨求实，追求卓越 高考文科数学 振文书院 ‎【答案】解:(Ⅰ)如图,在平面ABC内,过点作直线,因为在平面外,BC在平面内,由直线与平面平行的判定定理可知,平面. ‎ 由已知,,是BC中点,所以BC⊥AD,则直线, ‎ 又因为底面,所以, ‎ 又因为AD,在平面内,且AD与相交, ‎ 所以直线平面 ‎ ‎(Ⅱ)过D作于E,因为平面,所以, ‎ 又因为AC,在平面内,且AC与相交,所以平面, ‎ 由,∠BAC,有,∠DAC, ‎ 所以在△ACD中,, ‎ 又,所以 ‎ 因此三棱锥的体积为 ‎ ．（2013年高考湖北卷（文））如图,某地质队自水平地面A,B,C三处垂直向地下钻探,自A点向下钻到A1处发现矿藏,再继续下钻到A2处后下面已无矿,从而得到在A处正下方的矿层厚度为.同样可得在B,C处正下方的矿层厚度分别为,,且. 过,的中点,且与直线平行的平面截多面体所得的截面为该多面体的一个中截面,其面积记为.‎ ‎(Ⅰ)证明:中截面是梯形;‎ ‎(Ⅱ)在△ABC中,记,BC边上的高为,面积为. 在估测三角形区域内正下方的矿藏储量(即多面体的体积)时,可用近似公式来估算. 已知,试判断与V的大小关系,并加以证明. ‎ 24‎ 严谨求实，追求卓越 高考文科数学 振文书院 第20题图 ‎【答案】(Ⅰ)依题意平面,平面,平面, ‎ 所以A1A2∥B1B2∥C1C2. 又,,,且 . ‎ 因此四边形、均是梯形. ‎ 由∥平面,平面,且平面平面, ‎ 可得AA2∥ME,即A1A2∥DE. 同理可证A1A2∥FG,所以DE∥FG. ‎ 又、分别为、的中点, ‎ 则、、、分别为、、、 的中点, ‎ 即、分别为梯形、的中位线. ‎ 因此 ,, ‎ 而,故,所以中截面是梯形. ‎ ‎(Ⅱ). 证明如下:‎ 由平面,平面,可得. ‎ 而EM∥A1A2,所以,同理可得. ‎ 由是△的中位线,可得即为梯形的高, ‎ 因此, ‎ 即. ‎ 又,所以. ‎ 于是. ‎ 由,得,,故. ‎ ．（2013年高考课标Ⅱ卷（文））如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点.‎ 24‎ 严谨求实，追求卓越 高考文科数学 振文书院 ‎(1) 证明: BC1//平面A1CD;‎ ‎(2) 设AA1= AC=CB=2,AB=2,求三棱锥C一A1DE的体积.‎ ‎【答案】‎ ‎ ‎ ．（2013年高考大纲卷（文））如图,四棱锥 都是边长为的等边三角形.‎ ‎(I)证明: (II)求点 ‎ ‎【答案】(Ⅰ)证明:取BC的中点E,连结DE,则ABED为正方形. ‎ 24‎ 严谨求实，追求卓越 高考文科数学 振文书院 ‎ ‎ 过P作PO⊥平面ABCD,垂足为O. ‎ 连结OA,OB,OD,OE. ‎ 由和都是等边三角形知PA=PB=PD, ‎ 所以OA=OB=OD,即点O为正方形ABED对角线的交点, ‎ 故,从而. ‎ 因为O是BD的中点,E是BC的中点, ‎ 所以OE//CD.因此,. ‎ ‎(Ⅱ)解:取PD的中点F,连结OF,则OF//PB. ‎ 由(Ⅰ)知,,故. ‎ 又,, ‎ 故为等腰三角形,因此,. ‎ 又,所以平面PCD. ‎ 因为AE//CD,平面PCD,平面PCD,所以AE//平面PCD. ‎ 因此,O到平面PCD的距离OF就是A到平面PCD的距离,而, ‎ 所以A至平面PCD的距离为1. ‎ ．（2013年高考安徽（文））如图,四棱锥的底面是边长为2的菱形,.已知 .‎ ‎(Ⅰ)证明:‎ ‎(Ⅱ)若为的中点,求三菱锥的体积.‎ ‎【答案】解: ‎ 24‎ 严谨求实，追求卓越 高考文科数学 振文书院 ‎ ‎ ‎(1)证明:连接交于点 ‎ ‎ ‎ 又是菱形 ‎ 而 ⊥面 ⊥ ‎ ‎(2) 由(1)⊥面 ‎ ‎= ‎ ‎ ‎ ．（2013年上海高考数学试题（文科））如图,正三棱锥底面边长为,高为,求该三棱锥的体积及表面积.‎ ‎【答案】‎ 24‎ 严谨求实，追求卓越 高考文科数学 振文书院 ‎ ‎ ‎ ‎ ．（2013年高考天津卷（文））如图, 三棱柱ABC-A1B1C1中, 侧棱A1A⊥底面ABC,且各棱长均相等. D, E, F分别为棱AB, BC, A1C1的中点. ‎ ‎(Ⅰ) 证明EF//平面A1CD; ‎ ‎(Ⅱ) 证明平面A1CD⊥平面A1ABB1; ‎ ‎(Ⅲ) 求直线BC与平面A1CD所成角的正弦值. ‎ ‎【答案】‎ 24‎ 严谨求实，追求卓越 高考文科数学 振文书院 ‎ ‎ ．（2013年高考重庆卷（文））(本小题满分12分,(Ⅰ)小问5分,(Ⅱ)小问7分)‎ 如题(19)图,四棱锥中,⊥底面,,, .zhangwlx 24‎ 严谨求实，追求卓越 高考文科数学 振文书院 ‎(Ⅰ)求证:⊥平面;‎ ‎(Ⅱ)若侧棱上的点满足,求三棱锥的体积.‎ ‎【答案】‎ ‎ ‎ ‎ ‎ ‎ ‎ ．（2013年高考江西卷（文））如图,直四棱柱ABCD – A1B1C1D1中,AB//CD,AD⊥AB,AB=2,AD=,AA1=3,E为CD上一点,DE=1,EC=3‎ 24‎ 严谨求实，追求卓越 高考文科数学 振文书院 ‎(1) 证明:BE⊥平面BB1C1C;‎ ‎(2) 求点B1 到平面EA1C1 的距离 ‎【答案】解.(1)证明:过B作CD的垂线交CD于F,则 ‎ 在 ‎ 在,故 ‎ 由 ‎ ‎(2) ‎ ‎, ‎ 同理, ‎ 因此.设点B1到平面的距离为d,则 ‎ ‎,从而 ‎ 24‎ 严谨求实，追求卓越