参数方程在高考中的应用

参数方程在高考中的应用

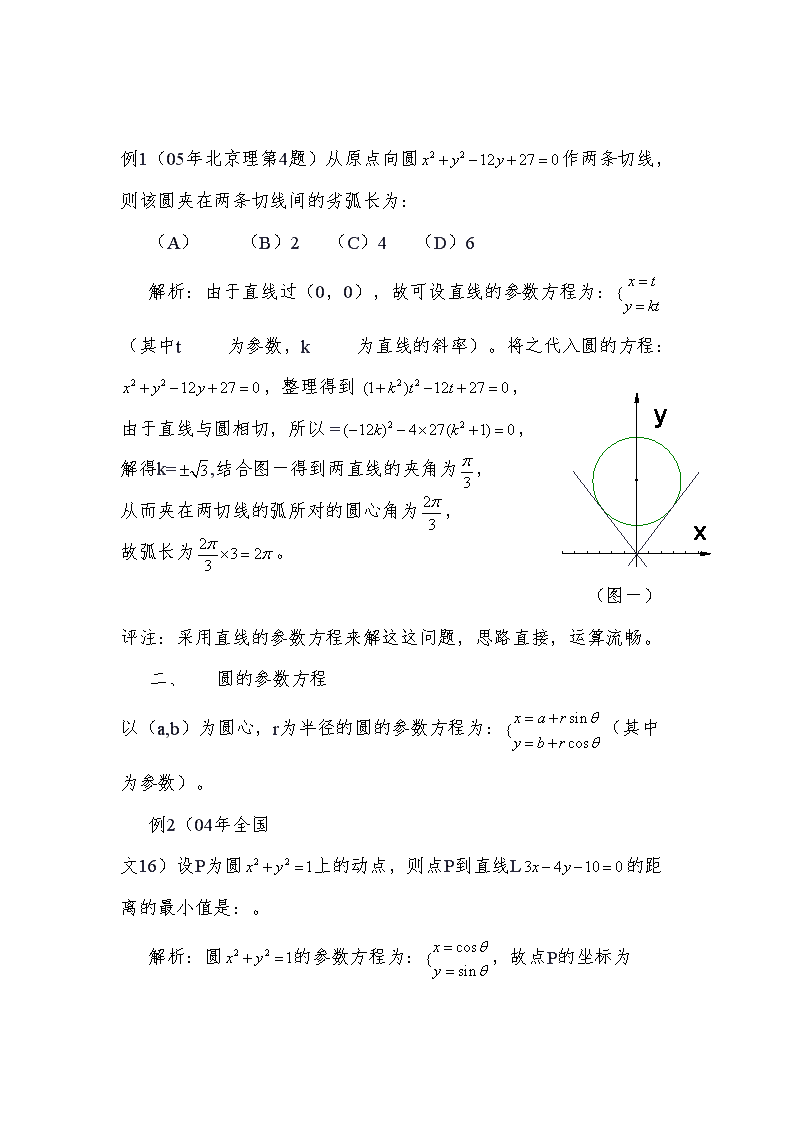
参数方程在高考中的应用 作者：蓝朝福，男，中学数学二级教师，大学本科，贵州省贵定第一中学教师。电话：13765433828；通讯地址：贵州贵定第一中学；邮编：551300‎ 文摘：圆锥曲线是解析几何的重点内容，它又有这样的特点：基础性强，要求对基础知识要熟练掌握并能灵活运用；综合性强，在解题中经常涉及到函数、方程、不等式、三角函数、等内容，它体现了对各种能力的综合要求。但高考试题中，往往会出现很多一道题有多种解法的题目，这不仅要求学生必需掌握一定的解题技巧和思想方法，还要掌握一定的知识面，才能应对高考中圆锥曲线这一部分的试题。‎ 关键词：直线 圆 椭圆 双曲线 参数方程 ‎ 高考《考试大纲》中，对解析几何部分的直线、圆、椭圆、双曲线的考查，没有明确地对它们的参数方程作出要求。但涉及到直线、圆、椭圆、双曲线的部分试题，若用其参数方程来解决，在化归、转换等环节会带来极大的方便，使得运算过程流畅，从而提高解题速度，节省时间去完成其他的题目，达到取得好成绩的目的。以下就以具体的历届高考题来体现参数方程的应用。‎ 一、 直线的参数方程 设直线L过定点P，=（a,b）为L上的方向向量，则直L的参数方程为：），特别地，若直线的斜率存在记为k，则 就是直线L的方向向量。‎ ‎ 例1（05年北京理第4题）从原点向圆作两条切线，则该圆夹在两条切线间的劣弧长为：‎ ‎（A） （B）2 （C）4 （D）6 解析：由于直线过（0，0），故可设直线的参数方程为：（其中t 为参数，k 为直线的斜率）。将之代入圆的方程：，整理得到 ，‎ 由于直线与圆相切，所以 =，‎ 解得k=,结合图一得到两直线的夹角为， ‎ 从而夹在两切线的弧所对的圆心角为， ‎ 故弧长为。‎ ‎（图一）评注：采用直线的参数方程来解这这问题，思路直接，运算流畅。‎ 一、 圆的参数方程 以（a,b）为圆心，r为半径的圆的参数方程为：（其中为参数）。‎ 例2（04年全国 文16）设P为圆上的动点，则点P到直线L的距离的最小值是：。‎ 解析：圆的参数方程为：，故点P的坐标为，由此得到点P到直线线L的距离 ，所以。（当时，为辅助角。）‎ 评注：本题采用圆的参数方程来解答，直接带点线距离公式，结合三角函数化简即可。当然，也可以用几何法来求，先求圆心到直线的距离，再减去圆的半径即可。‎ 一、 椭圆的参数方程 长轴长为‎2a、短轴长为2b、中心为、焦点在直线上的椭圆的参数方程为：（其中为参数）。‎ 例3（07年四川理第20题）设、分别是椭圆的左右焦点。‎ （1） 若P是该椭圆上的一个动点，求的最小值和最大值。‎ （2） 设过定点M（0，2）的直线L与椭圆交于不同的两点A、B，且AOB为锐角（其中O为坐标原点），求直线的斜率k的取值范围。‎ 解析：（1）易知椭圆的半焦距c=,所以设椭圆的参数方程为：（其中为参数），由此动点P的坐标为，则=，故==，的最小值为：-2；最大值为：1。‎ ‎（2）设直线L与椭圆的交点A、B的坐标分别为，依题意，可设直线L的参数方程为：（其中t为参数），将之代入椭圆方程，整理得：，，，而=0，解之得到：或。又为锐角 0，‎ 化简得：解之得，所以或。‎ ‎ 评注：此题运用直线和椭圆的参数方程来解答，（1）只是简单的三角函数的化简就可以推理出其最值：（2）运用直线的参数方程，只需要代入椭圆方程即可得出关于t的二次方程，再结合题意建立关于k的不等式组，思路清析，化归难度不大。‎ 一、 双曲线的参数方程 ‎ 实轴长为‎2a虚轴长为2b中心为、焦点在直线上的双曲线的参数方程为：（其中为参数）。‎ ‎ 例4 （05年全国Ш第9题）已知双曲线的焦点为，点M在双曲线上且，则点M到x轴的距离为：‎ ‎ （A） （B） （C） （D） ‎ 解析：设双曲线的参数方程为：（其中为参数），则点M的坐标为，知易，所以 可得到=0，化简得，解得||=，所以点M到x轴的距离为：。‎ 评注：此题采用双曲线的参数方程解答，简捷明快，不用解二次方程。‎ 运用圆锥曲线的参数来解题，思路清析，运算流畅，主要考查代入化简能力，知识点主要涉及三角函数的运用。‎ 参考文献：《全日制普通高级中学教科书》第二册。‎ ‎ 《高考试题》‎