- 2021-05-13 发布 |
- 37.5 KB |
- 15页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
非常好高考立体几何专题复习
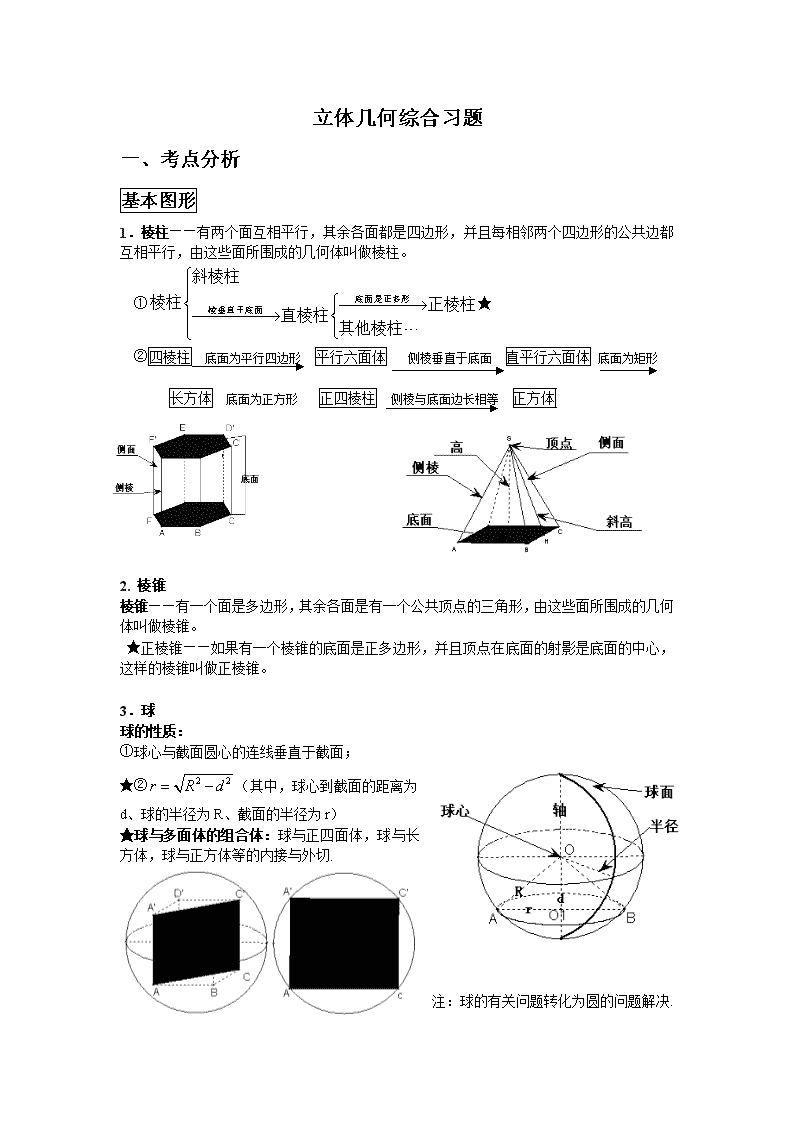
立体几何综合习题 一、考点分析 基本图形 1.棱柱——有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的几何体叫做棱柱。 ①★ ②四棱柱 底面为平行四边形 平行六面体 侧棱垂直于底面 直平行六面体 底面为矩形 长方体 底面为正方形 正四棱柱 侧棱与底面边长相等 正方体 2. 棱锥 棱锥——有一个面是多边形,其余各面是有一个公共顶点的三角形,由这些面所围成的几何体叫做棱锥。 ★正棱锥——如果有一个棱锥的底面是正多边形,并且顶点在底面的射影是底面的中心,这样的棱锥叫做正棱锥。 3.球 球的性质: ①球心与截面圆心的连线垂直于截面; ★②(其中,球心到截面的距离为d、球的半径为R、截面的半径为r) ★球与多面体的组合体:球与正四面体,球与长方体,球与正方体等的内接与外切. 注:球的有关问题转化为圆的问题解决. 平行垂直基础知识网络★★★ 平行关系 平面几何知识 线线平行 线面平行 面面平行 垂直关系 平面几何知识 线线垂直 线面垂直 面面垂直 判定 性质 判定推论 性质 判定 判定 性质 判定 面面垂直定义 1. 2. 3. 4. 5. 平行与垂直关系可互相转化 异面直线所成的角,线面角,二面角的求法★★★ 1.求异面直线所成的角: 解题步骤:一找(作):利用平移法找出异面直线所成的角;(1)可固定一条直线平移 另一条与其相交;(2)可将两条一面直线同时平移至某一特殊位置。常用中位线平移法 二证:证明所找(作)的角就是异面直线所成的角(或其补角)。常需要证明线线平行; 三计算:通过解三角形,求出异面直线所成的角; 2求直线与平面所成的角:关键找“两足”:垂足与斜足 解题步骤:一找:找(作)出斜线与其在平面内的射影的夹角(注意三垂线定理的应用); 二证:证明所找(作)的角就是直线与平面所成的角(或其补角)(常需证明线面垂直);三计算:常通过解直角三角形,求出线面角。 3求二面角的平面角 解题步骤:一找:根据二面角的平面角的定义,找(作)出二面角的平面角; 二证: 证明所找(作)的平面角就是二面角的平面角(常用定义法,三垂线法,垂面法); 三计算: 通过解三角形,求出二面角的平面角。 二、典型例题 考点一:三视图 2 2 侧(左)视图 2 2 2 正(主)视图 1.一空间几何体的三视图如图1所示,则该几何体的体积为_________________. 俯视图 第1题 2.若某空间几何体的三视图如图2所示,则该几何体的体积是________________. 第2题 第3题 3.一个几何体的三视图如图3所示,则这个几何体的体积为 . 4.若某几何体的三视图(单位:cm)如图4所示,则此几何体的体积是 . 3 正视图 俯视图 1 1 2 左视图 a 第4题 第5题 5.如图5是一个几何体的三视图,若它的体积是,则 . 6.已知某个几何体的三视图如图6,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是 . 20 20 正视图 20 侧视图 10 10 20 俯视图 第6题 第7题 7.若某几何体的三视图(单位:)如图所示,则此几何体的体积是 8.设某几何体的三视图如图8(尺寸的长度单位为m),则该几何体的体积为_________m3。 俯视图 正(主)视图 侧(左)视图 2 3 2 2 第7题 第8题 9.一个空间几何体的主视图和左视图都是边长为1的正方形,俯视图是一个圆,那么这个几何体的侧面积为_________________. 图9 10.一个三棱柱的底面是正三角形,侧棱垂直于底面,它的三视图及其尺寸如图10所示(单位cm),则该三棱柱的表面积为_____________. 俯视图 正视图 图10 11. 如图11所示,一个空间几何体的主视图和左视图都是边长为1的正方形,俯视图是一个直径为1的圆,那么这个几何体的全面积为_____________. 图 图11 图12 图13 12. 如图12,一个空间几何体的主视图和左视图都是边长为1的正三角形,俯视图是一个圆,那么几何体的侧面积为_____________. 13.已知某几何体的俯视图是如图13所示的边长为的正方形,主视图与左视图是边长为的正三角形,则其表面积是_____________. 14.如果一个几何体的三视图如图14所示(单位长度: ), 则此几何体的表面积是_____________. 图14 15.一个棱锥的三视图如图图9-3-7,则该棱锥的全面积(单位:)_____________. 正视图 左视图 俯视图 图15 16.图16是一个几何体的三视图,根据图中数据,可得该几何体的表面积是_____________. 俯视图 正(主)视图 侧(左)视图 2 3 2 2 图16 图17 17.如图17,一个空间几何体的主视图、左视图、俯视图为全等的等腰直角三角形,如果直角三角形的直角边长为1,那么这个几何体的体积为______________. 18.若一个底面为正三角形、侧棱与底面垂直的棱柱的三视图如图9-3-14所示,则这个棱柱的体积为______________. 图18 考点二 体积、表面积、距离、角 注:1-6体积表面积 7-11 异面直线所成角 12-15线面角 1. 将一个边长为a的正方体,切成27个全等的小正方体,则表面积增加了___________. 2. 在正方体的八个顶点中,有四个恰好是正四面体的顶点,则正方体的表面积与此正四面体的表面积的比值为___________. 3.设正六棱锥的底面边长为1,侧棱长为,那么它的体积为_______________. 4.正棱锥的高和底面边长都缩小原来的,则它的体积是原来的______________. 5.已知圆锥的母线长为8,底面周长为6π,则它的体积是 . 6.平行六面体的体积为30,则四面体的体积等于 . 7.如图7,在正方体中,分别是,中点,求异面直线与所成角的角______________. 8. 如图8所示,已知正四棱锥S—ABCD侧棱长为,底面边长为,E是SA的中点,则异面直线BE与SC所成角的大小为_____________. 第8题 第7题 9.正方体中,异面直线和所成的角的度数是_________________. 10.如图9-1-3,在长方体中,已知,则异面直线与所成的角是_________,异面直线与所成的角的度数是______________ 图13 11. 如图9-1-4,在空间四边形中, ,分别是AB、CD的中点,则 与所成角的大小为_____________. 12. 正方体中,与平面所成的角为 . 13.如图13在正三棱柱中,,则直线与平面所成角的正弦值为_______________. 14. 如图9-3-6,在正方体ABCD—A1B1C1D1中,对角线BD1与平面ABCD所成的角的正切值为_______________. A1 C B A B1 C1 D1 D O 图9-3-6 15.如图9-3-1,已知为等腰直角三角形,为空间一点,且,,,的中点为,则与平面所成的角为 16.如图7,正方体ABCD-A1B1C1D1的棱长为1,O是底面A1B1C1D1的中心,则O到平面AB C1D1的距离为__________________. 17.一平面截一球得到直径是6cm的圆面,球心到这个平面的距离是4cm,则该球的体积是______________. 18.长方体的8个顶点在同一个球面上,且AB=2,AD=, ,则顶点A、B间的球面距离是_________________. 19.已知点在同一个球面上,若,则两点间的球面距离是 . 20. 在正方体ABCD—A1B1C1D1中,M为DD1的中点,O为底面ABCD的中心,P为棱A1B1上任意一点,则直线OP与直线AM所成的角是_________________. 21.△ABC的顶点B在平面a内, A、C在a的同一侧,AB、BC与a所成的角分别是30°和45°,若AB=3,BC= ,AC=5,则AC与a所成的角为_________. 22.矩形ABCD中,AB=4,BC=3,沿AC将矩形ABCD折成一个直二面角B-AC-D, 则四面体ABCD的外接球的体积为_____________. 23.已知点在同一个球面上,若,则两点间的球面距离是 . 24.正三棱锥的一个侧面的面积与底面积之比为2∶3,则这个三棱锥的侧面和底面所成二面角的度数为________ . 25.已知是球表面上的点,,,, ,则球表面积等于____________. 26.已知正方体的八个顶点都在球面上,且球的体积为,则正方体的棱长为_________. 27. 一个四面体的所有棱长都为,四个顶点在同一球面上,则此球的表面积为_________. 考点四 平行与垂直的证明 1. 正方体,,E为棱的中点. (Ⅰ) 求证:; (Ⅱ) 求证:平面; (Ⅲ)求三棱锥的体积. 2.已知正方体,是底对角线的交点.求证:(1) C1O∥面;(2)面. 3.如图,矩形所在平面,、分别是和的中点. (Ⅰ)求证:∥平面; (Ⅱ)求证:; (Ⅲ)若,求证:平面. 4. 如图(1),ABCD为非直角梯形,点E,F分别为上下底AB,CD上的动点,且。现将梯形AEFD沿EF折起,得到图(2) (1)若折起后形成的空间图形满足,求证:; E B C F D A 图(2) (2)若折起后形成的空间图形满足四点共面,求证:平面; A B C D E F 图(1) A F E B C D M N 5.如图,在五面体ABCDEF中,FA 平面ABCD, AD//BC//FE,ABAD,M为EC的中点, N为AE的中点,AF=AB=BC=FE=AD (I) 证明平面AMD平面CDE; (II) 证明平面CDE; 6.在四棱锥P-ABCD中,侧面PCD是正三角形, 且与底面ABCD垂直,已知菱形ABCD中∠ADC=60°, P D A B C O M M是PA的中点,O是DC中点. (1)求证:OM // 平面PCB; (2)求证:PA⊥CD; (3)求证:平面PAB⊥平面COM. 7.如图,在四棱锥P—ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F. (1)证明PA//平面EDB;(2)证明PB⊥平面EFD 8.正四棱柱ABCD-A1B1C1D1的底面边长是,侧棱长是3,点E,F分别在BB1, DD1上,且AE⊥A1B,AF⊥A1D. (1)求证:A1C⊥面AEF; (2)求二面角A-EF-B的大小; (3)点B1到面AEF的距离. 考点五 异面直线所成的角,线面角,二面角 1. 如图,四棱锥P—ABCD的底面ABCD为正方形,PD⊥底面ABCD,PD=AD. 求证:(1)平面PAC⊥平面PBD; (2)求PC与平面PBD所成的角; 2.如图所示,已知正四棱锥S—ABCD侧棱长为,底面边长为,E是SA的中点,则异面直线BE与SC所成角的大小为 _____________. 3.正六棱柱ABCDEF-A1B1C1D1E1F1底面边长为1,侧棱长为,则这个棱柱的侧面对角线E1D与BC1所成的角是___________________. 4. 若正四棱锥的底面边长为2cm,体积为4cm3,则它的侧面与底面所成的二面角的大小是________. 5. 如图,在底面为平行四边形的四棱锥P-ABCD中,平面ABCD,且PA=AB,点E是PD的中点. (1)求证:; (2)求证:平面AEC; (3)若,求三棱锥E-ACD的体积; (4)求二面角E-AC-D的大小. 考点六 线面、面面关系判断题 1.已知直线l、m、平面α、β,且l⊥α,mβ,给出下列四个命题: (1)α∥β,则l⊥m (2)若l⊥m,则α∥β (3)若α⊥β,则l∥m (4)若l∥m,则α⊥β 其中正确的是__________________. 2. 是空间两条不同直线,是空间两条不同平面,下面有四个命题: ① ② ③ ④ 其中真命题的编号是________(写出所有真命题的编号)。 3. 为一条直线,为三个互不重合的平面,给出下面三个命题: ①;②;③. 其中正确的命题有_________________. 4. 对于平面和共面的直线、 (1)若则 (2)若则 (3)若则 (4)若、与所成的角相等,则 其中真命题的序号是_____________. 5. 关于直线m、n与平面与,有下列四个命题: ①若且,则; ②若且,则; ③若且,则; ④若且,则; 其中真命题的序号是_________________. 6. 已知两条直线,两个平面,给出下面四个命题: ① ② ③ ④ 其中正确命题的序号是_______________. 7.给出下列四个命题, 其中假命题的个数是______________. ①垂直于同一直线的两条直线互相平行; ②垂直于同一平面的两个平面互相平行. ③若直线与同一平面所成的角相等,则互相平行. ④若直线是异面直线,则与都相交的两条直线是异面直线. 查看更多