- 2021-05-13 发布 |
- 37.5 KB |
- 17页
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
南充市白塔中学月高考数学模拟题
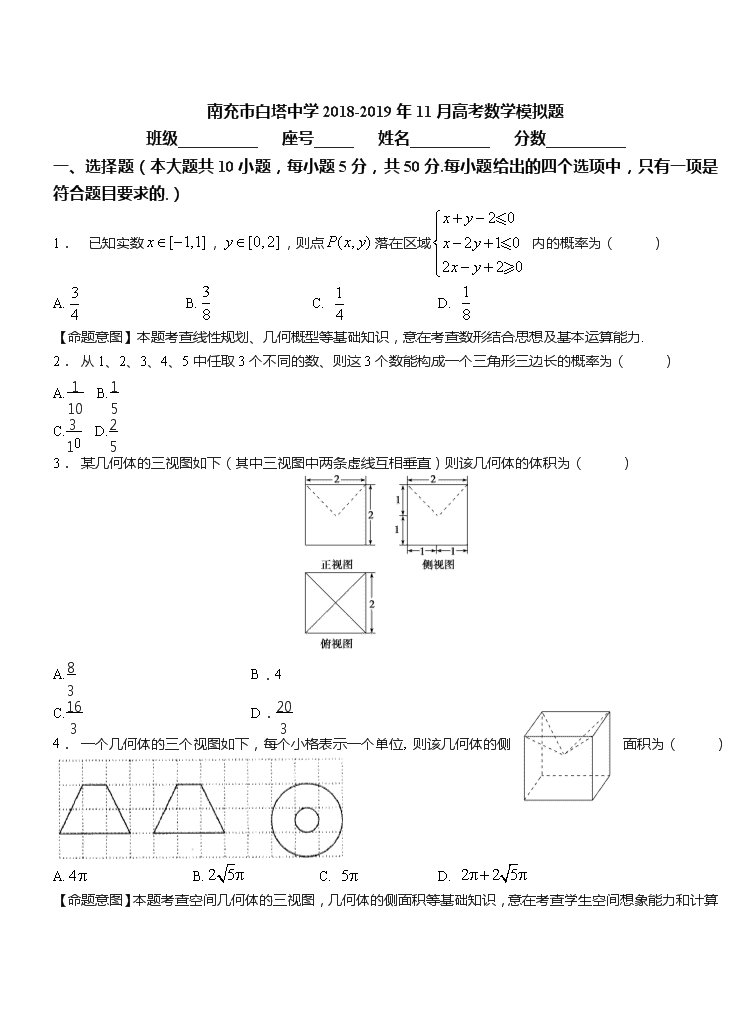
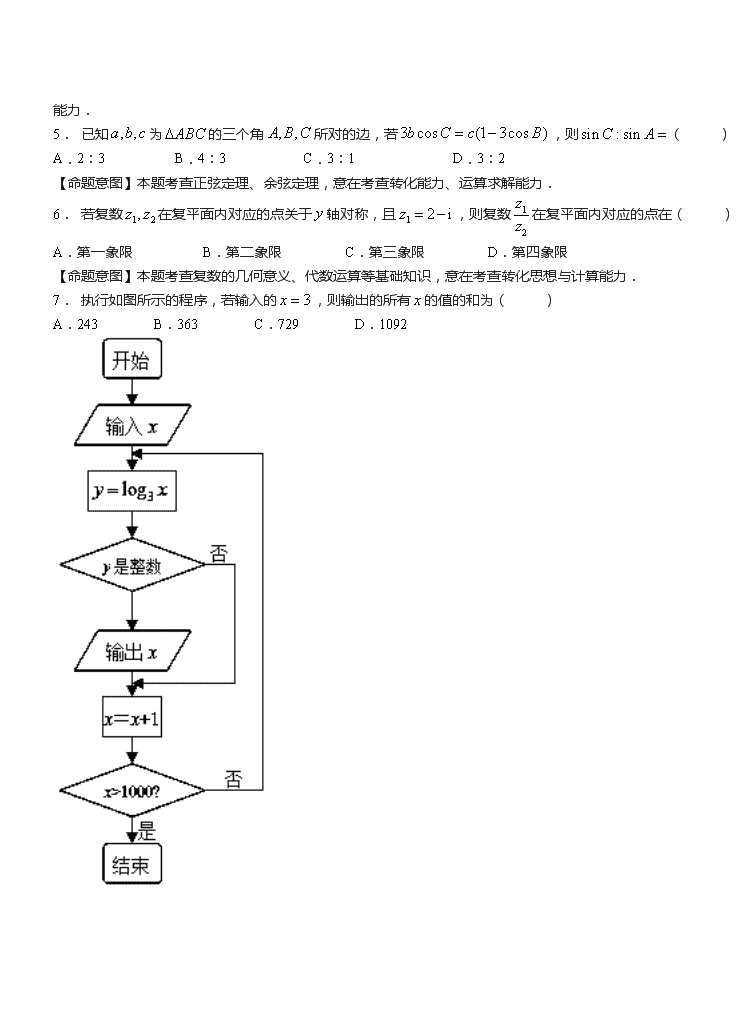
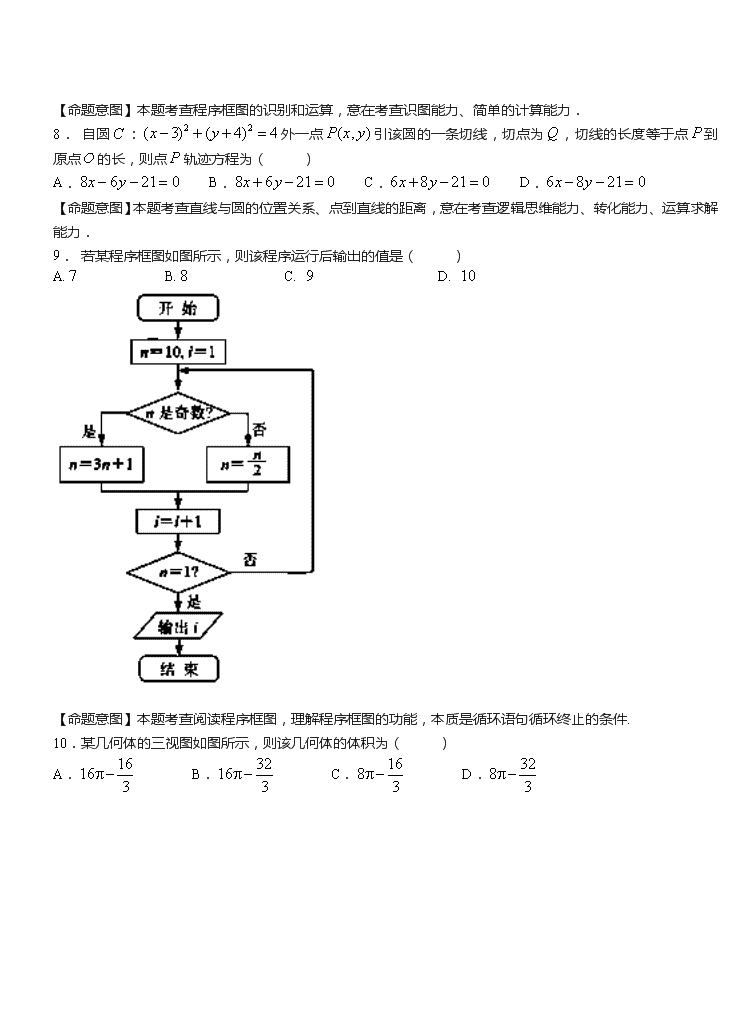
南充市白塔中学2018-2019年11月高考数学模拟题 班级__________ 座号_____ 姓名__________ 分数__________ 一、选择题(本大题共10小题,每小题5分,共50分.每小题给出的四个选项中,只有一项是符合题目要求的.) 1. 已知实数,,则点落在区域 内的概率为( ) A. B. C. D. 【命题意图】本题考查线性规划、几何概型等基础知识,意在考查数形结合思想及基本运算能力. 2. 从1、2、3、4、5中任取3个不同的数、则这3个数能构成一个三角形三边长的概率为( ) A. B. C. D. 3. 某几何体的三视图如下(其中三视图中两条虚线互相垂直)则该几何体的体积为( ) A. B.4 C. D. 4. 一个几何体的三个视图如下,每个小格表示一个单位, 则该几何体的侧面积为( ) A. B. C. D. 【命题意图】本题考查空间几何体的三视图,几何体的侧面积 等基础知识,意在考查学生空间想象能力和计算能力. 5. 已知为的三个角所对的边,若,则( ) A.2︰3 B.4︰3 C.3︰1 D.3︰2 【命题意图】本题考查正弦定理、余弦定理,意在考查转化能力、运算求解能力. 6. 若复数在复平面内对应的点关于轴对称,且,则复数在复平面内对应的点在( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限 【命题意图】本题考查复数的几何意义、代数运算等基础知识,意在考查转化思想与计算能力. 7. 执行如图所示的程序,若输入的,则输出的所有的值的和为( ) A.243 B.363 C.729 D.1092 【命题意图】本题考查程序框图的识别和运算,意在考查识图能力、简单的计算能力. 8. 自圆:外一点引该圆的一条切线,切点为,切线的长度等于点到原点的长,则点轨迹方程为( ) A. B. C. D. 【命题意图】本题考查直线与圆的位置关系、点到直线的距离,意在考查逻辑思维能力、转化能力、运算求解能力. 9. 若某程序框图如图所示,则该程序运行后输出的值是( ) A. B. C. D. 【命题意图】本题考查阅读程序框图,理解程序框图的功能,本质是循环语句循环终止的条件. 10.某几何体的三视图如图所示,则该几何体的体积为( ) A. B. C. D. 【命题意图】本题考查三视图、圆柱与棱锥的体积计算,意在考查识图能力、转化能力、空间想象能力. 二、填空题(本大题共5小题,每小题5分,共25分.把答案填写在横线上) 11.如图,在三棱锥中,,,,为等边三角形,则 与平面所成角的正弦值为______________. 【命题意图】本题考查空间直线与平面所成角的概念与计算方法,意在考查学生空间想象能力和计算能力. 12.数列{ an}中,a1=2,an+1=an+c(c为常数),{an}的前10项和为S10=200,则c=________. 13.设,实数,满足,若,则实数的取值范围是___________. 【命题意图】本题考查二元不等式(组)表示平面区域以及含参范围等基础知识,意在考查数形结合的数学思想与运算求解能力. 14.直线与抛物线交于,两点,且与轴负半轴相交,若为坐标原点,则 面积的最大值为 . 【命题意图】本题考查抛物线的几何性质,直线与抛物线的位置关系等基础知识,意在考查分析问题以及解决问题的能力. 15.已知函数,则的值是_______,的最小正周期是______. 【命题意图】本题考查三角恒等变换,三角函数的性质等基础知识,意在考查运算求解能力. 三、解答题(本大共6小题,共75分。解答应写出文字说明、证明过程或演算步骤。) 16.(本题满分15分) 若数列满足:(为常数, ),则称为调和数列,已知数列为调和数列,且,. (1)求数列的通项; (2)数列的前项和为,是否存在正整数,使得?若存在,求出的取值集合;若不存在,请说明理由. 【命题意图】本题考查数列的通项公式以及数列求和基础知识,意在考查运算求解能力. 17.(本小题满分12分)△ABC的三内角A,B,C的对边分别为a,b,c,AD是BC边上的中线. (1)求证:AD=; (2)若A=120°,AD=,=,求△ABC的面积. 18.(本题满分12分)有人在路边设局,宣传牌上写有“掷骰子,赢大奖”.其游戏规则是这样的:你可以 在1,2,3,4,5,6点中任选一个,并押上赌注元,然后掷1颗骰子,连续掷3次,若你所押的点数 在3次掷骰子过程中出现1次, 2次,3次,那么原来的赌注仍还给你,并且庄家分别给予你所押赌注的 1倍,2倍,3倍的奖励.如果3次掷骰子过程中,你所押的点数没出现,那么你的赌注就被庄家没收. (1)求掷3次骰子,至少出现1次为5点的概率; (2)如果你打算尝试一次,请计算一下你获利的期望值,并给大家一个正确的建议. 19.(本题满分15分) 已知函数,当时,恒成立. (1)若,,求实数的取值范围; (2)若,当时,求的最大值. 【命题意图】本题考查函数单调性与最值,分段函数,不等式性质等基础知识,意在考查推理论证能力,分析问题和解决问题的能力. 20.(本小题满分10分)直线l的极坐标方程为θ=α(ρ∈R,ρ≠0),其中α∈[0,π),曲线C1的参数方程为(t为参数),圆C2的普通方程为x2+y2+2x=0. (1)求C1,C2的极坐标方程; (2)若l与C1交于点A,l与C2交于点B,当|AB|=2时,求△ABC2的面积. 21.(本小题满分12分)已知分别是椭圆:的两个焦点,且,点在该椭圆上. (1)求椭圆的方程; (2)设直线与以原点为圆心,为半径的圆上相切于第一象限,切点为,且直线与椭圆交于两点,问是否为定值?如果是,求出定值,如不是,说明理由. 南充市白塔中学2018-2019年11月高考数学模拟题(参考答案) 一、选择题(本大题共10小题,每小题5分,共50分.每小题给出的四个选项中,只有一项是符合题目要求的.) 1. 【答案】B 【解析】不等式组表示的平面区域为,其中,,,所以.不等式组表示的平面区域为矩形,其中,,,其面积为,故所求概率为,选B. 2. 【答案】 【解析】解析:选C.从1、2、3、4、5中任取3个不同的数有下面10个不同结果:(1,2,3),(1,2,4),(1,2,5),(1,3,4),(1,3,5),(1,4,5),(2,3,4),(2,3,5),(2,4,5),(3,4,5),能构成一个三角形三边的数为(2,3,4),(2,4,5),(3,4,5),故概率P=. 3. 【答案】 【解析】选D.根据三视图可知,该几何体是一个棱长为2的正方体挖去一个以正方体的中心为顶点,上底面为底面的正四棱锥后剩下的几何体如图,其体积V=23-×2×2×1=,故选D. 4. 【答案】B 5. 【答案】C 【解析】由已知等式,得,由正弦定理,得,则,所以,故选C. 6. 【答案】B 【解析】 7. 【答案】D 【解析】当时,是整数;当时,是整数;依次类推可知当时,是整数,则由,得,所以输出的所有的值为3,9,27,81,243,729,其和为1092,故选D. 8. 【答案】D 【解析】由切线性质知,所以,则由,得,,化简得,即点的轨迹方程,故选D, 9. 【答案】A 【解析】运行该程序,注意到循环终止的条件,有n10,i1;n5,i2;n16,i3;n8,i4;n4,i5;n2,i6;n1,i7,到此循环终止,故选 A. 10.【答案】D 【解析】由三视图知几何体为一个底面半径为2高为4的半圆柱中挖去一个以轴截面为底面高为2的四棱锥,因此该几何体的体积为,故选D. 二、填空题(本大题共5小题,每小题5分,共25分.把答案填写在横线上) 11.【答案】 【解析】 12.【答案】 【解析】解析:由a1=2,an+1=an+c,知数列{an}是以2为首项,公差为c的等差数列,由S10=200得 10×2+×c=200,∴c=4. 答案:4 13.【答案】. 【解析】 14.【答案】 【解析】 15.【答案】,. 【解析】∵,∴,又∵,∴的定义域为,,将的图象如下图画出,从而可知其最小正周期为,故填:,. 三、解答题(本大共6小题,共75分。解答应写出文字说明、证明过程或演算步骤。) 16.【答案】(1),(2)详见解析. 当时,…………13分 ∴存在正整数,使得的取值集合为,…………15分 17.【答案】 【解析】解: (1)证明:∵D是BC的中点, ∴BD=DC=. 法一:在△ABD与△ACD中分别由余弦定理得c2=AD2+-2AD· cos∠ADB,① b2=AD2+-2AD··cos∠ADC,② ①+②得c2+b2=2AD2+, 即4AD2=2b2+2c2-a2, ∴AD=. 法二:在△ABD中,由余弦定理得 AD2=c2+-2c·cos B =c2+-ac· =, ∴AD=. (2)∵A=120°,AD=,=, 由余弦定理和正弦定理与(1)可得 a2=b2+c2+bc,① 2b2+2c2-a2=19,② =,③ 联立①②③解得b=3,c=5,a=7, ∴△ABC的面积为S=bc sin A=×3×5×sin 120°=. 即△ABC的面积为. 18.【答案】 【解析】【命题意图】本题考查了独立重复试验中概率的求法,对立事件的基本性质;对化归能力及对实际问题的抽象能力要求较高,属于中档难度. 19.【答案】 【解析】(1);(2). (1)由且,得, 当时,,得,…………3分 故的对称轴,当时,,………… 5分 解得,综上,实数的取值范围为;…………7分 ,…………13分 且当,,时,若,则恒成立, 且当时,取到最大值.的最大值为2.…………15分 20.【答案】 【解析】解:(1)由C1:(t为参数)得 x2+(y-1)2=1, 即x2+y2-2y=0, ∴ρ2-2ρsin θ=0,即ρ=2sin θ为C1的极坐标方程, 由圆C2:x2+y2+2x=0得 ρ2+2ρcos θ=0,即ρ=-2cos θ为C2的极坐标方程. (2)由题意得A,B的极坐标分别为 A(2sin α,α),B(-2cos α,α). ∴|AB|=|2sin α+2cos α| =4|sin(α+)|,α∈[0,π), 由|AB|=2得|sin(α+)|=, ∴α=或α=. 当α=时,B点极坐标(0,)与ρ≠0矛盾,∴α=, 此时l的方程为y=x·tan(x<0), 即x+3y=0,由圆C2:x2+y2+2x=0知圆心C2的直角坐标为(-,0), ∴C2到l的距离d==, ∴△ABC2的面积为S=|AB|·d =×2×=. 即△ABC2的面积为. 21.【答案】 【解析】【命题意图】本题考查椭圆方程与几何性质、直线与圆的位置关系等基础知识,意在考查逻辑思维能力、探索性能力、运算求解能力,以及方程思想、转化思想的应用.查看更多