- 2021-05-13 发布 |
- 37.5 KB |
- 9页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
上海高考数学复习卷含答案
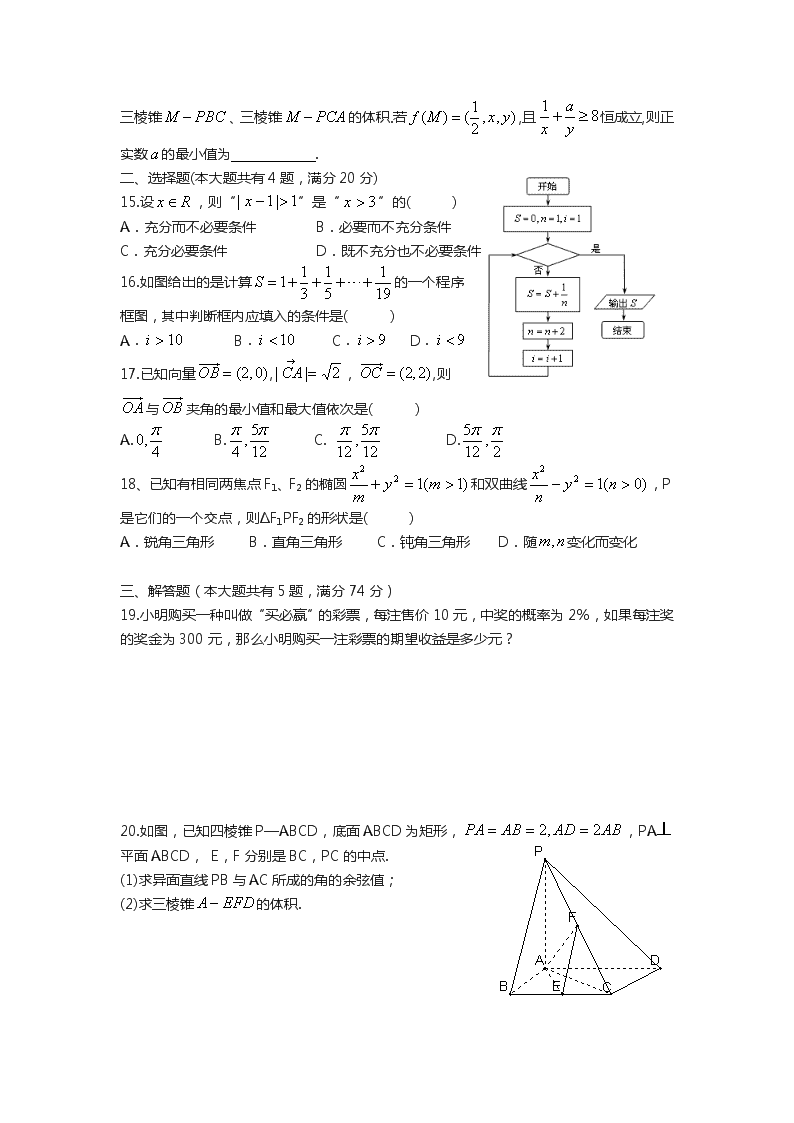
数学复习卷115 班级 姓名 学号 内容:第二轮复习 高一~高三全部教材内容 一、填空题:(本大题满分56分,每小题4分) 1.已知向量,若向量与垂直,则等于 . 2.已知= . 3.不等式的解集为 . 4.已知球的表面积为20,则该球的体积为 . 5.函数的反函数为,则 . 6.圆的极坐标方程为,则该圆的半径为 . 7.二项式的展开式中的系数为,则实数等于 . 8.在中,角所对的边分别是,若,,则的面积等于 . 9.在半径为的圆内作内接正六边形,再作正六边形的内切圆,又在此内切圆内作内接正六边形,如此无限继续下去,设为前个圆的面积之和,则= . 10.已知关于的实系数一元二次方程有实数根,则的最小值为 . 11.对于定义在上的函数,有下述命题: ①若是奇函数,则的图象关于点A(1,0)对称 ②若函数的图象关于直线对称,则为偶函数 ③若对,有2是的一个周期为 ④函数的图象关于直线对称. 其中正确的命题是 .(写出所有正确命题的序号) 12.从集合中随机选取一个数记为,从集合中随机选取一个数记为,则直线不经过第三象限的概率为 . 13.设定义域为的函数 若关于的函数的零点的个数为 . 14.如上图,在三棱锥中, 、、两两垂直,且.设是底面内一点,定义,其中、、分别是三棱锥、 三棱锥、三棱锥的体积.若,且 恒成立,则正实数的最小值为 . 二、选择题(本大题共有4题,满分20分) 15.设,则“”是“”的( ) A.充分而不必要条件 B.必要而不充分条件 C.充分必要条件 D.既不充分也不必要条件 16.如图给出的是计算的一个程序框图,其中判断框内应填入的条件是( ) A. B. C. D. 17.已知向量,,,则与夹角的最小值和最大值依次是( ) A. B. C. D. 18、已知有相同两焦点F1、F2的椭圆和双曲线,P是它们的一个交点,则ΔF1PF2的形状是( ) A.锐角三角形 B.直角三角形 C.钝角三角形 D.随变化而变化 三、解答题(本大题共有5题,满分74分) 19.小明购买一种叫做“买必赢”的彩票,每注售价10元,中奖的概率为2%,如果每注奖的奖金为300元,那么小明购买一注彩票的期望收益是多少元? 20.如图,已知四棱锥P—ABCD,底面ABCD为矩形,,PA平面ABCD, E,F分别是BC,PC的中点. (1)求异面直线PB与AC所成的角的余弦值; (2)求三棱锥的体积. 21.已知数列是各项均不为的等差数列,公差为,为其前项和,且满足 ,.数列满足,为数列的前项和. (1)求、和;(2)若对任意的,不等式恒成立,求实数的取值范围; 22.定义:对函数,对给定的正整数,若在其定义域内存在实数,使得,则称函数为“性质函数”。 (1)判断函数是否为“性质函数”?说明理由; (2)若函数为“2性质函数”,求实数的取值范围; (3)已知函数与的图像有公共点,求证:为“1性质函数”。 23.设抛物线的焦点为,过且垂直于轴的直线与抛物线交于两点,已知. (1)求抛物线的方程; (2)设,过点作方向向量为的直线与抛物线相交于两点,求使为钝角时实数的取值范围; (3)①对给定的定点,过作直线与抛物线相交于两点,问是否存在一条垂直于轴的直线与以线段为直径的圆始终相切?若存在,请求出这条直线;若不存在,请说明理由。 ②对,过作直线与抛物线相交于两点,问是否存在一条垂直于轴的直线与以线段为直径的圆始终相切?(只要求写出结论,不需用证明) 答案 一、填空题(共14题,每题4分,共56分) 1、2 2、 3、 4、 5、 6、(理) 7、(理)2 8、(理) 9、(理) 10、(理) 11、(理)①②③④ 12、 13、(理)7 14、1 二、选择题(共4题,每题5分,共20分) 15、B 16、A 17、(理)C 18、B 三、解答题 19、(本题满分12分) 解:2%+(-10)98%…………………… 8分 =-4(元) ……………………………. 10分 答:所求期望收益是-4元。 ……………………………. 12分 20、(本题满分14分,第(1)小题8分,第(2)小题6分) 解: (1)建立如图所示的空间直角坐标系,则, ,,……………………………. 4分 设与所成的角为,,…………………. 6分 异面直线PB与AC所成角的余弦值为。…………………. 8分 (2)。 ……………………………. 14分 (2)取中点E,连接DE,则, 为异面直线与所成角(或其补角)。………………….8分 中,,…………………………. 10分 设,则,……………………. 12分 因此异面直线与所成角的大小为。 ……………………………. 14分 21、(本题满分14分,第(1)小题6分,第(2)小题8分) 解:(1).……………………………. 1分 ,,当时,不满足条件,舍去.因此 .……………………………. 4分 ,,。 ……………………………. 6分 (2)当为偶数时,, ,当时等号成立,最小值为, 因此。 ……………………………. 9分 当为奇数时,, 在时单调递增,时的最小值为, 。 ……………………………. 12分 综上,。 ……………………………. 14分 22、(本题满分16分,第(1)小题4分,第2小题6分,第3小题6分) 解:(1)若存在满足条件,则即, ……………………………. 2分 ,方程无实数根,与假设矛盾。不能为 “k性质函数”。 ……………………………. 4分 (2)由条件得:,…………………. 5分 即(,化简得 ,……………………………. 7分 当时,;……………………………. 8分 当时,由, 即, 。 综上,。 ……………………………. 10分 (3)由条件存在使,即。…………………….11分 ,, ……………………………. 12分 ,……………………………. 14分 令, 则,………………………. 15分 ,为“1性质函数”。 ……………………………. 16分 23、(本题满分18分,第(1)小题4分,第2小题6分,第3小题8分) 解: (1)由条件得,抛物线C的方程为; ……………………………. 4分 (理)(2)直线方程为代入得, 设,则, 。……………………………. 6分 为钝角,,即 , , ……………………………. 8分 因此,………………. 9分 综上得。 ……………………………. 10分 (理)(3)①设过所作直线方程为代入得 ,…………………………….11 分 设则, ,中点,…………………. 12分 。………………………. 13分 设存在直线满足条件,则, ……………………………. 14分 对任意恒成立, 无解,这样的直线不存在。 …………………. 16分 ②当时,存在直线满足条件;………………………….17分 当且时,直线不存在。 …………………………….18分查看更多