- 2021-05-13 发布 |
- 37.5 KB |
- 14页

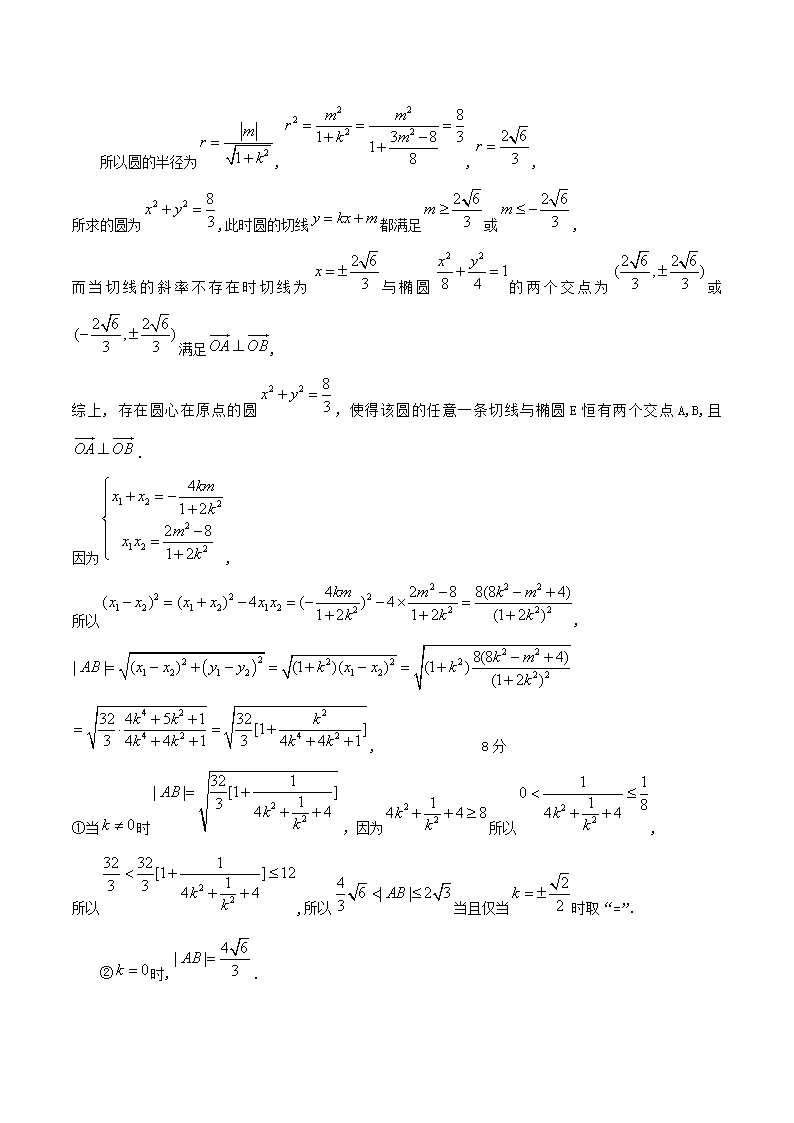

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
新课标高考数学一轮复习 名校尖子生培优大专题 圆锥曲线训练 新人教A版
名校专题----圆锥曲线培优训练5 1、设椭圆E: (a,b>0)过M(2,) ,N(,1)两点,O为坐标原点. (Ⅰ)求椭圆E的方程; (Ⅱ)是否存在圆心在原点的圆,使得该圆的任意一条切线与椭圆E恒有两个交点A,B, 且?若存在,写出该圆的方程,并求|AB |的取值范围,若不存在说明理由。 解:(1)因为椭圆E: (a,b>0)过M(2,),N(,1)两点, 所以解得所以椭圆E的方程为 4分 (2)假设存在圆心在原点的圆,使得该圆的任意一条切线与椭圆E恒有两个交点A,B,且,设该圆的切线方程为解方程组得, 即, 则△=,即 要使,需使,即,所以, 所以又, 所以,所以,即或, 因为直线为圆心在原点的圆的一条切线, 所以圆的半径为,,, 所求的圆为,此时圆的切线都满足或, 而当切线的斜率不存在时切线为与椭圆的两个交点为或满足, 综上, 存在圆心在原点的圆,使得该圆的任意一条切线与椭圆E恒有两个交点A,B,且. 因为, 所以, , 8分 ①当时,因为所以, 所以,所以当且仅当时取“=”. ②时,. ③当AB的斜率不存在时, 两个交点为或, 所以此时, 12分 综上, |AB |的取值范围为即: 14分 2、如图,已知椭圆的中心在原点,焦点在轴上,长轴长是短轴长的2倍且经过点M(2,1),平行于OM的直线l在轴上的截距为,l交椭圆于A、B两个不同点. (1)求椭圆的方程; (2)求m的取值范围; (3)求证直线MA、MB与轴始终围成一个等腰三角形. 解:(1)设椭圆方程为 则 2分 ∴椭圆方程 4分 (2)∵直线l平行于OM,且在轴上的截距为m,又 ∴l的方程为: 由 6分 ∵直线l与椭圆交于A、B两个不同点, ∴m的取值范围是 (3)设直线MA、MB的斜率分别为k1,k2,只需证明k1+k2=0即可 设 可得 8分 而 10分 ∴k1+k2=0 故直线MA、MB与x轴始终围成一个等腰三角形. 12分 3已知椭圆:()过点,其左、右焦点分别为,且 . (1)求椭圆的方程; (2)若是直线上的两个动点,且,则以为直径的圆是否过定点?请说明理由. 解:(1)设点的坐标分别为, 则 故,可得, …………………2分 所以,…………………4分 故, 所以椭圆的方程为. ……………………………6分 (2)设的坐标分别为,则, 又,可得,即, …………………8分 又圆的圆心为半径为, 故圆的方程为, 即, 也就是, ……………………11分 令,可得或2, 故圆必过定点和. ……………………13分 (另法:(1)中也可以直接将点坐标代入椭圆方程来进行求解;(2)中可利用圆C直径的两端点直接写出圆的方程) 4、已知点是直角坐标平面内的动点,点到直线的距离为,到点的距离为,且. (1)求动点P所在曲线C的方程; (2)直线过点F且与曲线C交于不同两点A、B(点A或B不在x轴上),分别过A、B点作直线的垂线,对应的垂足分别为,试判断点F与以线段为直径的圆的位置关系(指在圆内、圆上、圆外等情况); (3)记,,(A、B、是(2)中的点),问是否存在实数,使成立.若存在,求出的值;若不存在,请说明理由. 进一步思考问题:若上述问题中直线、点、曲线C:,则使等式成立的的值仍保持不变.请给出你的判断 (填写“不正确”或“正确”)(限于时间,这里不需要举反例,或证明). 解 (1) 设动点为,依据题意,有,化简得. 3分 因此,动点P所在曲线C的方程是:.……………4分 (2) 点F在以MN为直径的圆的外部. 理由:由题意可知,当过点F的直线的斜率为0时,不合题意,故可设直线: ,如图所示. 5分 联立方程组,可化为, 则点的坐标满足. 7分 又、,可得点、. 因,,则=.……9分 于是,为锐角,即点F在以MN为直径的圆的外部. 10分 (3)依据(2)可算出,, 则 , .…… 14分 所以,,即存在实数使得结论成立. ……15分 对进一步思考问题的判断:正确. ……18分 5、已知点是直角坐标平面内的动点,点到直线(是正常数)的距离为,到点的距离为,且1. (1)求动点P所在曲线C的方程; (2)直线过点F且与曲线C交于不同两点A、B,分别过A、B点作直线的垂线,对应的垂足分别为,求证=; (3)记,,(A、B、是(2)中的点),,求的值. 解 (1) 设动点为,依据题意,有 ,化简得.……4分 因此,动点P所在曲线C的方程是:. ……………6分 由题意可知,当过点F的直线的斜率为0时,不合题意, 故可设直线:,如图所示. …… 8分 联立方程组,可化为, 则点的坐标满足. 10分 又、,可得点、. 于是,,, 因此. 12分 (3)依据(2)可算出,, 则 , . 16分 所以,即为所求. 18分 6、已知:椭圆(),过点,的直线倾斜角为 ,原点到该直线的距离为. (1)求椭圆的方程; (2)斜率大于零的直线过与椭圆交于,两点,若,求直线的方程; (3)是否存在实数,直线交椭圆于,两点,以为直径的圆过点?若存在,求出的值;若不存在,请说明理由. 解:(1)由, ,得,, 所以椭圆方程是:……………………4分 (2)设EF:()代入,得, 设,,由,得. 由,……………………8分 得,,(舍去),(没舍去扣1分) 直线的方程为:即……………………10分 (3)将代入,得(*) 记,,PQ为直径的圆过,则,即,又,,得.………………14分 解得,此时(*)方程,存在,满足题设条件.…………16分 7、已知点,动点满足条件,记动点的轨迹为。 (1)求的方程; (2)过作直线交曲线于两点,使得2,求直线的方程。 (3)若从动点向圆:作两条切线,切点为、,令|PC|=d, 试用d来表示,并求的取值范围。 解:(1)由,知点的轨迹是以为焦点,实轴长为的双曲线 即设,所以所求的的方程为 4分 (2)若k不存在,即x=2时,可得A(2,),B(2,-),|AB|=2满足题意; 5分 若k存在,可设l:y=k(x-2) 联立, 由题意知且 6分 设A(x1,y1),B(x2,y2),则|AB|= 即 =2 k=0 即l:y=0 8分 所以直线l的方程为 x=0或y=0 9分 (3) 又 则----- 13分 在是增函数, 则所求的的范围为。 16分 8、在平面直角坐标系中,已知焦距为4的椭圆的左、右顶点分别为,椭圆 的右焦点为,过作一条垂直于轴的直线与椭圆相交于,若线段的长为。 (1)求椭圆的方程; (2)设是直线上的点,直线与椭圆分别交于点,求证:直线 必过轴上的一定点,并求出此定点的坐标; (3)实际上,第(2)小题的结论可以推广到任意的椭圆、双曲线以及抛物线,请你对抛物线写出一个更一般的结论,并加以证明。 A B Q O M N x y 9 (1)依题意,椭圆过点,故,解得。………(3分) 椭圆的方程为。…………(4分) (2)设,直线的方程为,……………(5分) 代入椭圆方程,得, ……(6分) 设,则,…(7分) ,故点的坐标为。………(8分) 同理,直线的方程为,代入椭圆方程,得, 设,则,。 可得点的坐标为。…………………………………………………………(10分) ①若时,直线的方程为,与轴交于点; ②若,直线的方程为, 令,解得。综上所述,直线必过轴上的定点。…………………………(12分) (3)结论:已知抛物线的顶点为,为直线上一动点,过点作 轴的平行线与抛物线交于点,直线与抛物线交于点,则直线必过定点。………(14分) 证明:设,则, P O M N x y 直线的方程为,代入,得,可求得。…(16分) 直线的方程为, 令,得,即直线必过定点。……(18分) 9、已知椭圆中心为,右顶点为,过定点作直线交椭圆于、两点. (1)若直线与轴垂直,求三角形面积的最大值; (2)若,直线的斜率为,求证:; (3)直线和的斜率的乘积是否为非零常数?请说明理由. 解:设直线与椭圆的交点坐标为. (1)把代入可得:, (2分) 则,当且仅当时取等号 (4分) (2)由得,,(6分) 所以 (9分) (3)直线和的斜率的乘积是一个非零常数. (11分) 当直线与轴不垂直时,可设直线方程为:, 由消去整理得 则 ① 又 ② (13分) 所以(15分) 当直线与轴垂直时,由得两交点, 显然.所以直线和的斜率的乘积是一个非零常数.(16分) 10、定义:由椭圆的两个焦点和短轴的一个顶点组成的三角形称为该椭圆的“特征三角形”。如果两个椭圆的“特征三角形”是相似的,则称这两个椭圆是“相似椭圆”,并将三角形的相似比称为椭圆的相似比。已知椭圆。 若椭圆,判断与是否相似?如果相似,求出与的相似比;如果不相似, 请说明理由; 写出与椭圆相似且短半轴长为的椭圆的方程;若在椭圆上存在两点、关于直线对称,求实数的取值范围? 如图:直线与两个“相似椭圆”和分别交于点和点,证明: 23.解:(1)椭圆与相似。-------------------2分 因为椭圆的特征三角形是腰长为4,底边长为的等腰三角形,而椭圆的特征三角形是腰长为2,底边长为的等腰三角形,因此两个等腰三角形相似,且相似比为-------------------4分 (2)椭圆的方程为:-------------------6分 设,点,中点为, 则,所以-------------------8分 则 -------------------9分 因为中点在直线上,所以有,-------------------10分 即直线的方程为:, 由题意可知,直线与椭圆有两个不同的交点, 即方程有两个不同的实数解, 所以,即-------------------12分 (3)证明: ①直线与轴垂直时,易得线段AB与CD的中点重合,所以;-------------------14分 ②直线不与轴垂直时,设直线的方程为:,, 线段AB的中点, -------------------15分 线段AB的中点为-------------------16分 同理可得线段CD的中点为,-------------------17分 即线段AB与CD的中点重合,所以-------------------18查看更多