辽宁省朝阳市中考数学试卷和答案

辽宁省朝阳市中考数学试卷和答案

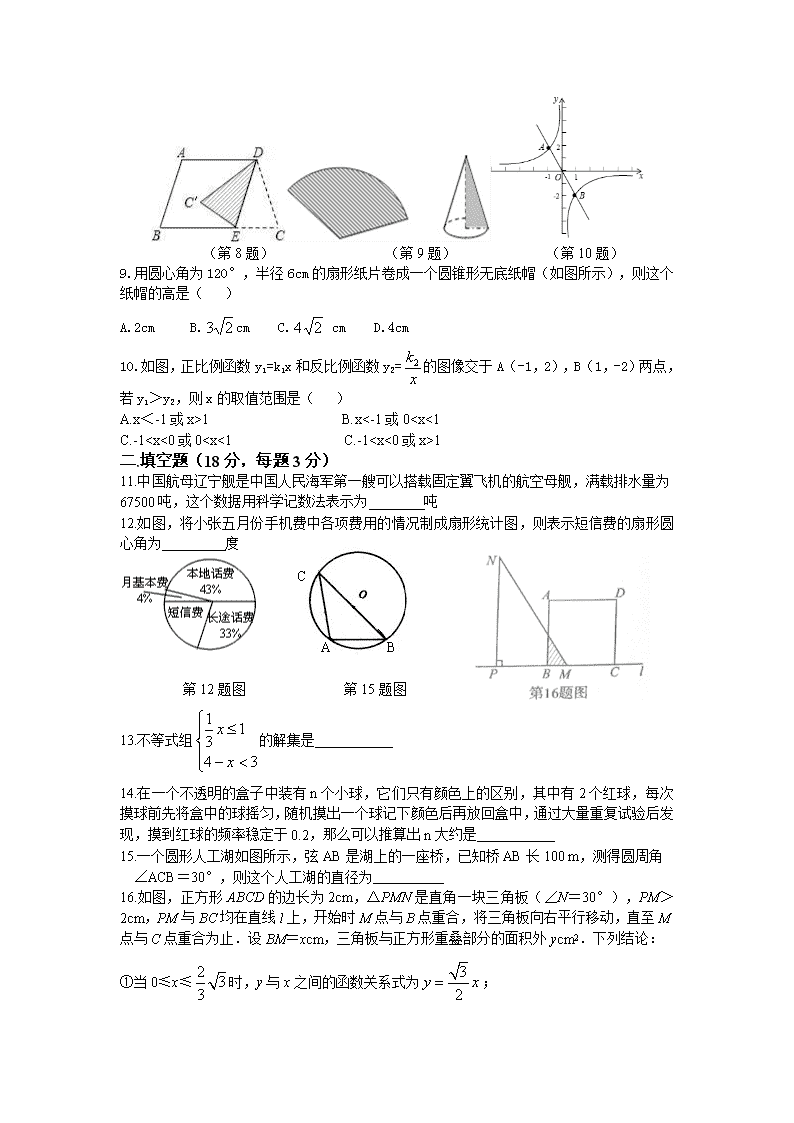
辽宁省朝阳市2014年中考试题 ‎（考试时间120分钟，满分120分）‎ 一.选择题（20分，每题2分）‎ ‎1.3的相反数是（ ）‎ A.3 B. C.-3 D.‎ 2. 如图所示几何体的左视图是（ ）‎ ‎ ‎ ‎ A B C D ‎3.某商店销售一种玩具，每件售价90元，可获利15％，求这种玩具的成本价．设这种玩具的成本价为x元，依题意列方程，正确的是（ ）‎ A． B． C．90－x＝15％ D． x＝90×15％‎ ‎4.如图，AB//CD，∠ABE=60°，∠D=50°，则∠E的度数为（ ）‎ ‎ （4题图） （6题图）‎ 5. 计算，结果正确的是（ ）‎ A. B. C. 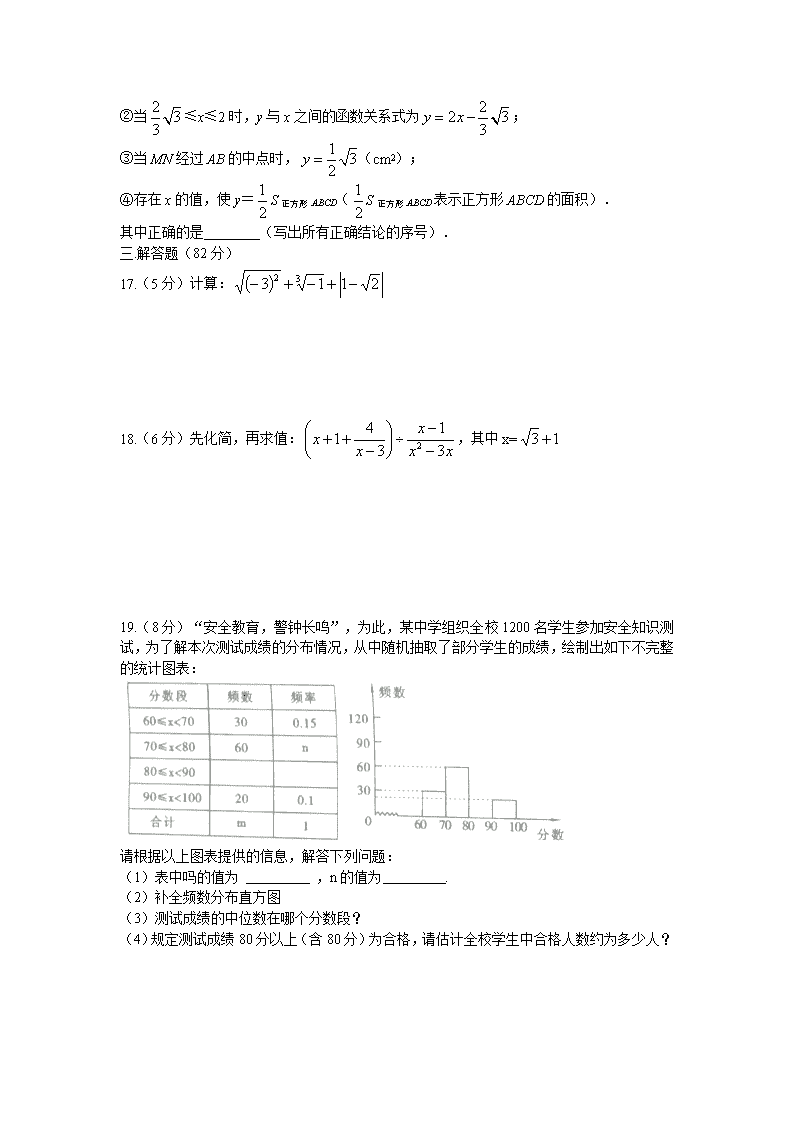D.‎ ‎6.如图，某地修建高速公路，要从B地向C地修一座隧道（B，C在同一水平面上），为了测量B，C两地之间的距离，某工程师乘坐热气球从C地出发，垂直上升100m到达A处，在A处观察B地的俯角为30°，则BC两地之间的距离为 （ ）‎ A.m B.m C.m D.‎ ‎7.六箱救灾区物资的质量（单位：千克）分别是17，20，18,17,18,18,则这组数据的平均数，众数，方差依次是（ ）‎ A.18，18，3 B.18，18，1 C.18，17.5，3 D.17.5，18，1‎ 8. 如图，在梯形ABCD中，AD//BC,AB=DC,∠ABC=72°，现平行移动腰AB至DE后，再将△DCE沿DE折叠，得△DC′E，则∠EDC′的度数是( )‎ A.72° B.54° C.36° D.30°‎ ‎ （第8题） （第9题） （第10题）‎ 8. 用圆心角为120°，半径6cm的扇形纸片卷成一个圆锥形无底纸帽（如图所示），则这个纸帽的高是（ ）‎ A.2cm B.cm C. cm D.4cm ‎10.如图，正比例函数y1=k1x和反比例函数y2=的图像交于A（-1，2），B（1，-2）两点，若y1＞y2，则x的取值范围是（ ）‎ A.x＜-1或x>1 B.x<-1或01 ‎ 二. 填空题（18分，每题3分）‎ 11. 中国航母辽宁舰是中国人民海军第一艘可以搭载固定翼飞机的航空母舰，满载排水量为67500吨，这个数据用科学记数法表示为 吨 12. 如图，将小张五月份手机费中各项费用的情况制成扇形统计图，则表示短信费的扇形圆心角为 度 C ‎ A B ‎ ‎ 第12题图 第15题图 13. 不等式组的解集是 ‎ 14. 在一个不透明的盒子中装有n个小球，它们只有颜色上的区别，其中有2个红球，每次摸球前先将盒中的球摇匀，随机摸出一个球记下颜色后再放回盒中，通过大量重复试验后发现，摸到红球的频率稳定于0.2，那么可以推算出n大约是 ‎ 15. 一个圆形人工湖如图所示，弦AB是湖上的一座桥，已知桥AB长100 m，测得圆周角 ‎ ∠ACB＝30°，则这个人工湖的直径为 ‎ ‎16.如图，正方形ABCD的边长为2cm，△PMN是直角一块三角板（∠N＝30°），PM＞2cm，PM与BC均在直线l上，开始时M点与B点重合，将三角板向右平行移动，直至M点与C点重合为止．设BM＝xcm，三角板与正方形重叠部分的面积外ycm2．下列结论：‎ ‎①当0≤x≤时，y与x之间的函数关系式为；‎ ‎②当≤x≤2时，y与x之间的函数关系式为；‎ ‎③当MN经过AB的中点时，（cm2）；‎ ‎④存在x的值，使y＝S正方形ABCD（S正方形ABCD表示正方形ABCD的面积）．‎ 其中正确的是________（写出所有正确结论的序号）．‎ 三. 解答题（82分）‎ 17. ‎（5分）计算：‎ 18. ‎（6分）先化简，再求值：，其中x=‎ 19. ‎（8分）“安全教育，警钟长鸣”，为此，某中学组织全校1200名学生参加安全知识测试，为了解本次测试成绩的分布情况，从中随机抽取了部分学生的成绩，绘制出如下不完整的统计图表：‎ 请根据以上图表提供的信息，解答下列问题：‎ （1） 表中吗的值为 ，n的值为 .‎ （2） 补全频数分布直方图 （3） 测试成绩的中位数在哪个分数段？‎ （4） 规定测试成绩80分以上（含80分）为合格，请估计全校学生中合格人数约为多少人？‎ ‎20.（7分）某工程开准备招标，指挥部现接到甲乙两个工程队的投标书，从投标书中得知：乙队单独完成这项工程所需天数是甲队单独完成这项工程所需天数的2倍；该工程若由甲队先做6天，剩下的工程再由甲、乙合作16天可以完成。求甲、乙两队单独完成这项工程各需多少天.‎ 21. ‎（8分）如图，O为矩形ABCD对角线的交点，DE//AC,CE//BD.‎ ‎(1)求证：四边形OCED是菱形 ‎ （2）若AB＝3，BC＝4，求四边形OCED的面积 22. ‎（8分）四张形状相同的卡片如图所示.将卡片洗匀后背面朝上放置在桌面上，小明先随机抽一张卡片，记下数字为x；小亮再随机抽一张卡片，记下数字为y.两人在此基础上共同协商一个游戏规则：当x>y时小明获胜，否则小亮获胜 （1） 若小明抽出的卡片不放回，求小明获胜的概率 （2） 若小明抽出的卡片放回后小亮再随机抽取，问他们制定的游戏规则公平吗？请说明 ‎ 理由.‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎ ‎ 23. ‎（8分）如图，AB是圆O的弦，OA⊥OD，AB，OD相交于点C，且CD=BD.‎ ‎ （1）判断BD与圆O的位置关系，并证明你的结论 ‎ （2）当OA=3，OC=1时，求线段BD的长.‎ ‎ ‎ 23. ‎（10分）长城汽车销售公司5月份销售某种型号汽车.当月该型号的进价为30万元/辆.‎ 若当月销售量超过5辆时，每多售出1辆，所有售出的汽车进价均降低0.1万元/辆．根据市场调查，月销售量不会突破30台．‎ ‎（1）设当月该型号汽车的销售量为x辆（x≤30，且x为正整数），实际进价为y万元/辆，求y与x的函数关系式；‎ ‎（2）已知该型号汽车的销售价为32万元/辆，公司计划当月销售利润25万元，那么月需售出多少辆汽车？（注：销售利润=销售价﹣进价）‎ ‎25.（10分）已知Rt△ABC中，AC=BC=2.一直角的顶点P在AB上滑动，直角的两边分别交线段AC，BC于E.F两点 ‎（1）如图1，当且PE⊥AC时，求证：；‎ ‎（2）如图2，当时（1）的结论是否仍然成立？为什么？‎ ‎（3）在（2）的条件下，将直角∠EPF绕点P旋转，设∠BPF＝α（0°＜α＜90°）．连结EF，当△CEF的周长等于时，请直接写出α的度数．‎ 26. ‎（12分）如图，平面直角坐标系中，抛物线y=ax2+bx+4经过点D（2，4),且与x轴交于A（3，0），B（-1，0）两点，与y轴交于点C，连接AC，CD，BC （1） 直接写出该抛物线的解析式 （2） 点P是所求抛物线上的一个动点，过点P作x轴的垂线l，l分别交x轴于点E，交直线AC于点M.设点P的横坐标为m.‎ ‎ ①当0≤m≤2时，过点M作MG//BC,MG交x轴于点G，连接GC，则m为何值时，△GMC的面积取得最大值，并求出这个最大值 ‎ ②当-1≤m≤2时，试探求：是否存在实数m，使得以P，C，M为顶点的三角形和△AEM相似？若存在，求出相应的m值；若不存在，请说明理由