中考数学压轴题及答案

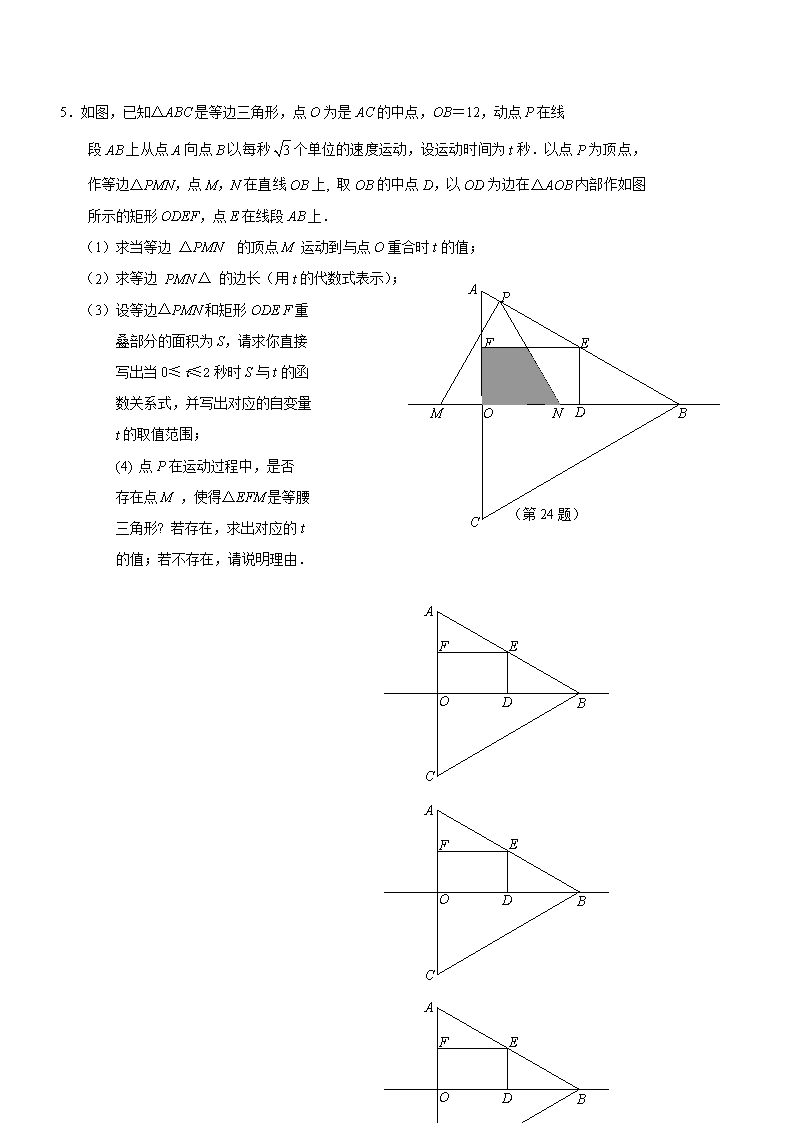
中考数学压轴题及答案

‎1．下图是由棋子组成的“正”字，则第6个图形需要棋子枚数为 ‎···‎ ‎···‎ ‎··‎ ‎·‎ ‎·‎ ‎（1）‎ ‎···‎ ‎···‎ ‎··‎ ‎·‎ ‎（2）‎ ‎·‎ ‎··‎ ‎··‎ ‎···‎ ‎···‎ ‎···‎ ‎·‎ ‎·‎ ‎（3）‎ ‎·‎ ‎··‎ ‎····‎ ‎····‎ ‎··‎ ‎·‎ ‎·‎ ‎·‎ ‎………‎ A．45 B．46 C．47 D．48‎ ‎（第10题）‎ ‎2.．如图，为二次函数的图象，给出的下列6个结论:‎ ‎①； ②方程的根为； ‎ ‎③； ④当时，y随x值的增大而增大；‎ ‎⑤当y＞0时，―＜x＜3; ⑥a＋b＋c＞0.‎ 其中正确的有 A．2个 B．3个 C．4个 D．5个 ‎. 3.如图，直角梯形ABCD中，∠DAB=90°，AB∥CD，AB=AD，∠ABC=60°．以AD为边在直角梯形ABCD外作等边三角形ADF，点E是直角梯形ABCD内一点，且∠EAD=∠EDA=15°，连接EB、EF．‎ ‎（1）求证：EB=EF；‎ ‎（2）若EF=6,求梯形ABCD的面积．‎ x(月)‎ ‎1‎ n (件)‎ O ‎6‎ ‎2‎ ‎30‎ ‎40‎ ‎（第25题）‎ ‎4. 近年来，我国高度重视节能环保，并出台了一系列扶持政策,节能环保已位列七大新兴产业之首.‎ 某公司销售A、B两种节能产品，已知今年1-6月份A产品每个月的销售数量p（件）与月份x（1≤x≤6且x为整数）之间的关系如下表：‎ 时间(月)‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ 售价p(元)‎ ‎600‎ ‎300‎ ‎200‎ ‎150‎ ‎120‎ ‎100‎ A产品每个月的售价q（元）与月份x之间的函数关系式为：‎ q=10x；已知B产品每个月的销售数量m（件）与月份x之 间的关系为：m=-5x+80，B产品每个月的售价n（元）与月 份x之间存在如图所示的变化趋势.‎ ‎（1）请观察题中表格及图像，用所学过的一次函数或反比例函数的有关知识，直接写 出p与x，n与x的函数关系式；‎ ‎（2）求出此商店1-6月份经营A、B两种产品的销售总额w与月份x之间的函数关系式，并求出在哪个月时获得最大销售总额；‎ ‎（3）今年7月份，商店调整了A、B两种产品的价格，A产品价格在6月份基础上减少0.5a%，B产品价格在6月份基础上增加0.5a%，结果7月份A产品的销售数量比6月份增加0.6a%，B产品的销售数量比6月份减少1.5a%．若调整价格后7月份的销售总额比6月份的销售总额少(1000―20a)元，请根据以下参考数据估算a的正整数值.‎ ‎（参考数据：） ‎ ‎ ‎ ‎ ‎ ‎5．如图，已知△ABC是等边三角形，点O为是AC的中点，OB＝12，动点P在线 段AB上从点A向点B以每秒个单位的速度运动，设运动时间为t秒．以点P为顶点，作等边△PMN，点M，N在直线OB上, 取OB的中点D，以OD为边在△AOB内部作如图所示的矩形ODEF，点E在线段AB上．‎ ‎（1）求当等边 △PMN 的顶点M 运动到与点O重合时t的值；‎ A P M F E D C B N O ‎（第24题）‎ ‎（2）求等边 PMN △ 的边长（用t的代数式表示）；‎ ‎（3）设等边△PMN和矩形ODE F重 叠部分的面积为S，请求你直接 写出当0≤t≤2秒时S与t的函 数关系式，并写出对应的自变量 t的取值范围；‎ ‎(4) 点P在运动过程中，是否 存在点M ，使得△EFM是等腰 三角形? 若存在，求出对应的t 的值；若不存在，请说明理由．‎ A F E D C B O A F E D C B O A F E D C B O ‎ ‎ ‎ ‎ ‎ ‎ ‎6．下列图形都是由同样大小的等边三角形按一定的规律组成，其中，第①个图形中一共有根小棒，第②个图形中一共有根小棒，第③个图形中一共有根小棒，……，则第⑥个图形中小棒的根数为 ‎ ‎ ‎……‎ ‎ ① ② ③‎ ‎ A． B． C． D．‎ ‎7．如图，矩形在平面直角坐标系中的位置如图所示，‎ ‎，.抛物线（）经 过点和点，与轴分别交于点、（点在点 左侧），且，则下列结论：①；②；③‎ ‎；④；⑤连接、，则 ‎，其中正确结论的个数为 第10题图 ‎ A．个 B．个 C．个 D．个 ‎8．如图，正方形中，为边上一点，过点作，与延长线交于点．连接，与边交于点，与对角线交于点．‎ ‎ （1）若，求的长；‎ ‎ （2）若，求证：．‎ 第24题图 ‎9. 金银花自古被誉为清热解毒的良药，同时也是很多高级饮料的常用原料．“渝蕾一号”为重庆市中药研究院所选育的金银花优良品种，较传统金银花具有质量好、产量高、结蕾整齐等优点．某花农于前年引进一批“渝蕾一号”金银花种苗进行种植，去年第一次收获．因金银花入药或作饮料需要使用干燥花蕾，该花农将收获的新鲜金银花全部干燥成干花蕾后出售．根据经验，每亩鲜花蕾产量（千克）与每亩种苗数（株）满足关系式：，每亩成本（元）与每亩种苗数（株）之间的函数关系满足下表：‎ 每亩种苗数（株）‎ ‎100‎ ‎110‎ ‎120‎ ‎130‎ ‎140‎ 每亩成本（元）‎ ‎1800‎ ‎1860‎ ‎1920‎ ‎1980‎ ‎2040‎ ‎（1）请观察题中的表格，用所学过的一次函数、反比例函数或二次函数的有关知识，求出与的函数关系式；‎ ‎（2）若该品种金银花的折干率为20%（即每100千克鲜花蕾，干燥后可得20千克干花蕾），去年每千克干花蕾售价为200元，则当每亩种苗数为多少时，每亩销售利润可获得最大值，并求出该最大利润；（利润=收入成本）‎ ‎（3）若该花农按照（2）中获得最大利润的方案种植，并不断改善养植技术，今年每亩鲜花蕾产量比去年增加%．但由于市场上同类产品数量猛增，造成每千克干花蕾的售价比去年降低%，结果今年每亩销售总额为45810元．请你参考以下数据，估算出的整数值（）．‎ ‎（参考数据：，，，）‎ ‎ ‎ ‎10．如图1，梯形中，∥，，．一个动点从点出发，以每秒个单位长度的速度沿线段方向运动，过点作，交折线段于，以为边向右作正方形，点在射线上，当点到达点时，运动结束．设点的运动时间为秒（）．‎ ‎ （1）当正方形的边恰好经过点时，求运动时间的值；‎ ‎ （2）在整个运动过程中，设正方形与△的重合部分面积为，请直接写 出与之间的函数关系式和相应的自变量的取值范围；‎ ‎ （3）如图2，当点在线段上运动时，线段与对角线交于点，将△ ‎ 沿翻折，得到△，连接．是否存在这样的 ,使△是等腰三角形？若存在，求出对应的的值；若不存在，请说明理由．‎ 第26题图1‎ 第26题图2‎ 备用图 ‎ ‎ ‎11.如图，直角梯形ABCD中，AD∥BC，∠ABC=90°，已知AD=AB=3，BC=4，动点P从B点出发，沿线段BC向点C作匀速运动；动点Q从点D出发，沿线段DA向点A作匀速运动．过Q点垂直于AD的射线交AC于点M，交BC于点N．P、Q两点同时出发，速度都为每秒1个单位长度．当Q点运动到A点，P、Q两点同时停止运动．设点Q运动的时间为t秒． （1）求NC，MC的长（用t的代数式表示）； （2）当t为何值时，四边形PCDQ构成平行四边形； （3）是否存在某一时刻，使射线QN恰好将△ABC的面积和周长同时平分？若存在，求出此时t的值；若不存在，请说明理由； （4）探究：t为何值时，△PMC为等腰三角形．‎ ‎12. 如图，已知在梯形中，于点，交于点，连接。‎ ‎（1）求证：； ‎ ‎ ‎ ‎（2）若，求梯形的面积。‎ ‎13. 血橙以果肉酷似鲜血的颜色而得名，它本质上属脐橙类，现在已经开发出多种品种，果实一般在1月下旬成熟。由于果农在生产实践中积累了丰富的管理经验，大多采取了留树保鲜技术措施，将鲜果供应期拉长到了5月初。重庆市万州区晚熟柑橘以血橙为主，其中沙河街孙家村是万州血橙老产区，主要销售市场是成都、重庆市区、万州城区。据以往经验，孙家村上半年1~5月血橙的售价（元/千克）与月份之间满足一次函数关系。其月销售量（千克）与月份之间的相关数据如下表：‎ 月份 ‎1月 ‎2月 ‎3月 ‎4月 ‎5月 销售量（千克）‎ ‎70000‎ ‎65000‎ ‎60000‎ ‎55000‎ ‎50000‎ ‎（1）请观察题中的表格，用所学过的一次函数，反比例函数或二次函数的有关知识，求月销售量（千克）与月份之间的函数关系式；‎ ‎（2）血橙在上半年1~5月的哪个月出售，可使销售金额（元）最大？最大金额是多少元？‎ ‎（3）由于气候适宜以及保鲜技术的提高，预计该产区今年5月将收获‎60000千克的血橙，并按（2）问中获得最大销售金额时的销售量售出新鲜血橙。剩下的血橙的果肉与石榴、白糖按5：2：1的比例制成“石榴·血橙白茶果冻”出售（以下简称“果冻”，制作过程中的损耗忽略不计），已知平均每千克的血橙含‎0.8千克的果肉。产区生产商最初将每千克果冻的批发价定为26元，超市的零售价比批发价高%，当销售了这批果冻的四分之三后，考虑到制作和营运成本的提高，生产商将批发价提高了%，超市的零售价也跟着在此批发价的基础上提高了%，最后该产区将这批果冻在超市全部出售后的销售总额达到了390000元。求的值。（结果保留整数）‎ ‎（参考数据：）‎ 答案 ‎1.A2.C ‎3. 解：（1）证明：∵△ADF为等边三角形，∴AF＝AD，∠FAD＝60° （1分）‎ ‎∵∠DAB＝90°，∠EAD＝15°，AD＝AB， （2分）‎ ‎∴∠FAE＝∠BAE＝75°，AB＝AF， （3分）‎ ‎∵AE为公共边　∴△FAE≌△BAE ∴EF＝EB. （5分） ‎ ‎（2）由题设可得△FAE≌△FDE（SSS）,∠DFE＝∠AFE＝60º/2＝30º,‎ ‎∠DEF＝∠AEF＝150º/2＝75º， (6分)‎ ‎ ∠FAE＝60º＋15º＝75º, ∴AF＝EF＝6, AB＝AD＝AF＝6, （7分）‎ ‎ 过C作CM⊥AB于M,则tan∠ABC＝CM/BM,‎ ‎∴ BM＝CM/tan60º＝6/＝2， （8分）‎ ‎ ∴ CD＝AB－BM＝6－ （9分）‎ ‎∴ 梯形ABCD的面积为 S＝. ‎ ‎4. .解：（1）p＝； n＝10x＋20； （2分）‎ ‎（2）w＝pq＋mn=×10x＋(―5x＋80)(10x＋20) ＝―50＋700x＋7600, （4分）‎ 对称轴， （5分） ∵ 开口向下，∴ 在对称轴左侧W随x的增大而增大，且 1≤x≤6, x为整数，‎ ‎∴ 当x＝6时，W最大＝―50×62＋700×6＋7600＝10000. ‎ ‎∴ 商店在6月份获得最大销售总额，这个最大销售总额为10000元. （6分）‎ ‎（3）今年6月份A产品的售价：q＝10×6＝60元，销售数量：p＝100 件 今年6月份B产品的售价：n＝10×6＋20＝80元，销售量：m＝―5×6＋80＝50（件），‎ ‎60(1―0.5a%)×100(1＋0.6a%)＋80(1＋0.5a%)×50(1―1.5a%)＝10000―(1000―20a)（8分）‎ 令t＝a%，整理得，， （9分）‎ ‎∴ , (舍去)‎ 图①‎ A B C P O(M)‎ N E F ‎∴ a＝100t≈16，∴ a的正整数值为16. ‎ ‎5. 解：（1）如图①点M与点O重合．‎ ‎_‎ A ‎∵ △ABC是等边三角形，O为AC中点, ‎ ‎_‎ D ‎∴ ∠AOP＝30°，∠APO＝90°， （1分）‎ 图②‎ A B C P O N E F M D 由OB＝12，得AO＝4＝2AP＝2t． (2分) ‎ 解得t＝2．∴ 当t＝2时，点M与点O重合. （3分）‎ ‎（2）如图②，由题设知∠ABM＝30°,AB＝8，AP＝t,‎ ‎ ∴ PB＝8－t （4分）‎ ‎∵ tan∠PBM＝PM/PB, (5分)‎ ‎∴ 等边△PMN的边长为 PM＝PB•tan∠PBM＝(8－t)tan30º＝8－t. （6分）‎ 图④‎ 图⑤‎ 图⑥‎ 图③‎ ‎（3）（Ⅰ）当0≤t≤1时，即PM经过线段AF，如图③．‎ 设PN交EF于点G，则重叠部分为直角梯形FONG，‎ ‎∴ S重叠＝2t＋6． （8分）‎ ‎（Ⅱ）当1＜t≤2时，即PM经过线段FO,‎ 设PM与FO交于Q,如图④．‎ 重叠部分为五边形OQJGN．‎ ‎∴ S重叠＝－2t2＋6t＋4． （9分）‎ ‎（4）∵MN＝BN＝PN＝8－t， ∴MB＝16－2 t ‎_‎ G ‎①当FM＝EM时，如图⑤，M为OD中点，∴OM＝3，‎ 由OM＋MB＝OB得3＋16－2t＝12，∴　t＝3.5， （10分）　 ‎ ‎②当FM＝FE＝6时，如图⑥，∴OM＝，‎ 由OM＋MB＝12得＋16－2 t＝12, ∴t＝.（11分）‎ ‎③当EF＝EM＝6时，点M可在OD或DB上，如图⑦，如图⑧，‎ DM＝，‎ ‎∴ DB＋DM＝MB,或者 DB－DM＝MB ‎∴ 6＋＝16－2 t 或者6－＝16－2 t ‎∴ t＝， 或者t＝. （12分） ‎ 图⑦‎ 图⑧‎ 综上所述，当t＝3.5，，，时，‎ ‎△MEF是等腰三角形. ‎ ‎6.B7.C ‎8（1）解：∵正方形 ‎∴Rt△中，‎ ‎ 即 ‎ ∴‎ ‎ ∵ ‎ ‎∴‎ ‎ ∵，‎ ‎∴△≌△‎ ‎ ∴‎ ‎ ∴ …………5分 第24题图 ‎ （2）证明：在上截取一段，使得 ‎ ∵△≌△‎ ‎∴‎ ‎ ∴△为等腰直角三角形 ‎∴‎ ‎∴△≌△ ‎ ‎∴‎ 又∵‎ ‎∴‎ ‎ ∵‎ ‎∴‎ ‎∴ 即△为等边三角形 ‎∴‎ ‎∴ …………10分 ‎9...解：（1）由表格知，为的一次函数，设（）‎ ‎∵当时，；当时，‎ ‎ ∴ 解得 ‎ ∴ …………1分 ‎ ‎ 当时，‎ ‎ 经检验，表格中每组数据均满足该关系式 ‎ ∴该函数关系式为 …………2分 ‎ （2）由题意知， …………3分 ‎ ‎ ‎ ‎ ‎ ∵‎ ‎∴当时，‎ ‎ ∴当每亩种苗数为株时，每亩销售利润可获得最大值，最大利润为元．‎ ‎ …………6分 ‎ （3）当时，‎ ‎ ∴ …………7分 ‎ 根据题意有 …………8分 ‎ 设，则原方程可化为 ‎ 解得 ‎ ‎ ∴，‎ ‎∴（舍去） ‎ ‎∴的值约为．‎ ‎10. .解：（1）作，，垂足分别为、‎ ‎ 则四边形为矩形 ‎ ∵梯形，‎ ‎ ∴△≌△‎ ‎ ∴，‎ ‎ ∴秒后，正方形的边长恒为 ‎ ∴当正方形的边恰好经过点时，点与点重合，此时 ‎ ∴，‎ ‎ ∴ 即秒时，正方形的边恰好经过点 …………2分 ‎ （2） …………6分 ‎（3）∵‎ ‎∴‎ 由（1）可知 ‎ 则 ‎ ①当时，‎ ‎ ∴‎ ‎ ②当时，作，垂足为 ‎ ∵‎ ‎∴‎ ‎∴‎ ‎③当时，作，垂足为 ‎ ∵‎ ‎∴‎ ‎∴‎ ‎∴当、或时，△是等腰三角形 …………12分 ‎11.(1)) ‎ ‎(2) t=2‎ ‎ （3）不存在，因为ΔABC的周长的一半=6≠‎ ‎ （4）分三种情况讨论 ‎ 当PM=MC时，ΔPMC为等腰三角形t= ‚当CM=PC时，ΔPMC为等腰三角形t=ƒ当PM=PC时，ΔPMC为等腰三角形t=‎ 综上所述，当t=， ，时ΔPMC为等腰三角形