河南中考中的证明题含答案

河南中考中的证明题含答案

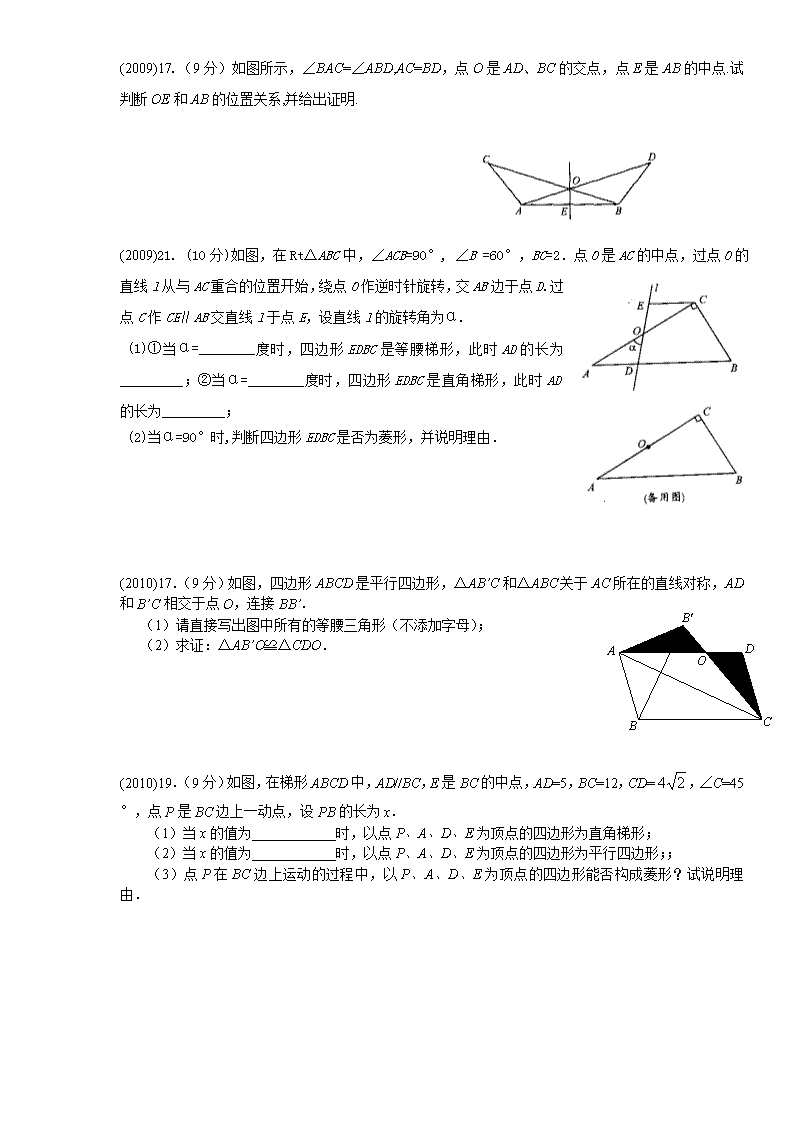
河南中考中的几何证明题 (2007)17．（9 分）如图，点 E、F、G 分别 是□ABCD 的边 AB、BC、CD、DA 的中点．求证：ΔBEF≌Δ DGH． (2007)20．（9 分）如图，ABCD 是边长为 1 的正方形，其中 、 、 的圆心依次是点 A、B、 C．（1）求点 D 沿三条圆弧运动到 G 所经过的路线长；（2）判断直线 GB 与 DF 的位置关系，并说明 理由． (2008)18．（9 分）复习“全等三角形”的知识时，老师布置了一道作业题：“如图①，已知在△ABC 中， AB=AC，P 是△ABC 内部任意一点，将 AP 绕 A 顺时针旋转至 AQ，使∠QAP=∠BAC，连接 BQ、CP， 则 BQ=CP．”小亮是个爱动脑筋的同学，他通过对图①的分析，证明了△ABQ≌△ACP，从而证得 BQ=CP 之后，将点 P 移到等腰三角形 ABC 之外，原题中的条件不变，发现“BQ=CP”仍然成立，请你就图②给 出证明． （2008）21．（9 分）如图，在平面直角坐标系中，点 A 的坐标是（10，0），点 B 的坐标为（8，0）， 点 C、D 在以 OA 为直径的半圆 M 上，且四边形 OCDB 是平行四边形．求点 C 的坐标． F G D E C B A ⌒ DE ⌒ EF ⌒ FG G H E F D CB A 图① Q P CB A A Q B P C 图② (2009)17.（9 分）如图所示，∠BAC=∠ABD,AC=BD，点 O 是 AD、BC 的交点，点 E 是 AB 的中点.试 判断 OE 和 AB 的位置关系,并给出证明. (2009)21. (10 分)如图，在 Rt△ABC 中，∠ACB=90°, ∠B =60°，BC=2．点 0 是 AC 的中点，过点 0 的 直线 l 从与 AC 重合的位置开始，绕点 0 作逆时针旋转，交 AB 边于点 D.过 点 C 作 CE∥AB 交直线 l 于点 E，设直线 l 的旋转角为α. (1)①当α=________度时，四边形 EDBC 是等腰梯形，此时 AD 的长为 _________；②当α=________度时，四边形 EDBC 是直角梯形，此时 AD 的长为_________； (2)当α=90°时,判断四边形 EDBC 是否为菱形，并说明理由． (2010)17．（9 分）如图，四边形 ABCD 是平行四边形，△AB’C 和△ABC 关于 AC 所在的直线对称，AD 和 B’C 相交于点 O，连接 BB’． （1）请直接写出图中所有的等腰三角形（不添加字母）； （2）求证：△AB’O≌△CDO． (2010)19．（9 分）如图，在梯形 ABCD 中，AD//BC，E 是 BC 的中点，AD=5，BC=12，CD= ，∠C=45 °，点 P 是 BC 边上一动点，设 PB 的长为 x． （1）当 x 的值为____________时，以点 P、A、D、E 为顶点的四边形为直角梯形； （2）当 x 的值为____________时，以点 P、A、D、E 为顶点的四边形为平行四边形；； （3）点 P 在 BC 边上运动的过程中，以 P、A、D、E 为顶点的四边形能否构成菱形？试说明理 由． 24 (2011)17. （9 分）如图，在梯形 ABCD 中，AD∥BC，延长 CB 到点 E，使 BE=AD，连接 DE 交 AB 于 点 M. （1）求证：△AMD≌△BME； （2）若 N 是 CD 的中点，且 MN=5，BE=2，求 BC 的长. (2012)18. （9 分）如图，在菱形 ABCD 中，AB=2，∠DAB=60°，点 E 是 AD 边的中点．点 M 是 AB 边上一动点（不与点 A 重合），延长 ME 交射线 CD 于点 N，连接 MD、AN． （1）求证：四边形 AMDN 是平行四边形； （2）填空：①当 AM 的值为_______时，四边形 AMDN 是矩形； ②当 AM 的值为________时，四边形 AMDN 是菱形． P E A B C D E A M B CDN 其他省市证明题 1 ．如图，在四边形 中，对角线 交于点 ， ． 求 的长和四边形 的面积． 答案： CD=2，面积=（3 根号 3+9）/2 2．已知：如图， 是 的直径， 是 上一点， 于点 ，过点 作 的切线，交 的延长线于点 ，连结 ． （1）求证： 与 相切； （2）连结 并延长交 于点 ，若 ，求 的 长． ABCD AC BD， E 90 45 30 2BAC CED DCE DE∠ = ° ∠ = ° ∠ = ° =， ， ， ， 2 2BE = CD ABCD AB O⊙ C O⊙ OD BC⊥ D C O⊙ OD E BE BE O⊙ AD BE F 9OB = ， 2sin 3ABC∠ = BF 3．如图，AD 是△ABC 的角平分线，过点 D 作 DE∥AB，DF∥AC，分别交 AC、AB 于点 E 和 F． （1）在图中画出线段 DE 和 DF； （2）连接 EF，则线段 AD 和 EF 互相垂直平分，这是为什么？ 考点： 菱形的判定与性质；作图—复杂作图。 分析： （1）根据题目要求画出线段 DE、DF 即可； （2）首先证明四边形 AEDF 是平行四边形，再证明∠EAD=∠EDA，根据等角对等边可得 EA=ED，由有一组邻边相等的平行四边形是菱形可证明四边形 AEDF 是菱形，再根据菱形的性 质可得线段 AD 和 EF 互相垂直平分． 解答： 解（1）如图所示； （2）∵DE∥AB，DF∥AC， ∴四边形 AEDF 是平行四边形， ∵AD 是△ABC 的角平分线， ∴∠FAD=∠EAD， ∵AB∥DE， ∴∠FAD=∠EDA， ∴∠EAD=∠EDA， ∴EA=ED， ∴平行四边形 AEDF 是菱形， ∴AD 与 EF 互相垂直平分． 点评： 此题主要考查了画平行线，菱形的判定与性质，关键是掌握菱形的判定方法，判定四边形为菱 形可以结合菱形的性质证出线段相等，角相等，线段互相垂直且平分． 4．如图，AB 是⊙O 的直径，AC 是弦，OD⊥AC 于点 D，过点 A 作⊙O 的切线 AP，AP 与 OD 的延长 线交于点 P，连接 PC、BC． （1）猜想：线段 OD 与 BC 有何数量和位置关系，并证明你的结论． （2）求证：PC 是⊙O 的切线． 考点： 切线的判定与性质；全等三角形的判定与性质；三角形中位线定理；圆周角定理。 分析： （1）根据垂径定理可以得到 D 是 AC 的中点，则 OD 是△ABC 的中位线，根据三角形的中位线 定理可以得到 OD∥BC，CD= BC； （2）连接 OC，设 OP 与⊙O 交于点 E，可以证得△OAP≌△OCP，利用全等三角形的对应角相 等，以及切线的性质定理可以得到：∠OCP=90°，即 OC⊥PC，即可等证． 解答： （1）猜想：OD∥BC，CD= BC． 证明：∵OD⊥AC， ∴AD=DC ∵AB 是⊙O 的直径， ∴OA=OB…2 分 ∴OD 是△ABC 的中位线， ∴OD∥BC，OD= BC （2）证明：连接 OC，设 OP 与⊙O 交于点 E． ∵OD⊥AC，OD 经过圆心 O， ∴ ，即∠AOE=∠COE 在△OAP 和△OCP 中， ∵OA=OC，OP=OP， ∴△OAP≌△OCP， ∴∠OCP=∠OAP ∵PA 是⊙O 的切线， ∴∠OAP=90°． ∴∠OCP=90°，即 OC⊥PC ∴PC 是⊙O 的切线． 点评： 本题考查了切线的性质定理以及判定定理，三角形的中位线定理，证明圆的切线的问题常用的 思路是根据切线的判定定理转化成证明垂直的问题． 5.如图所示，在 ， ， 是边 的中点， ，垂足为 ，已知 ， . ①求线段 的长； ②求 的值. 答案：① ② 6.如图所示，在菱形 中，点 、 分别在 、 上， ， 与 相交于点 . ①求证： ； ②当 时，求证：四边形 是平行四边形. Rt ABC 90ACB∠ = ° D AB BE CD⊥ E 15AC = 3 5cosA = CD sin DBE∠ 25 2 7 25 ABCD E F BC CD BAF DAE∠ = ∠ AE BD G BE DF= DF AD FC DF = BEFG E D BC A E D CB A FG 7.(8 分）如图，在△ABC 中，BA=BC，以AB 为直径作半圆⊙O， 交AC 于点D.连结DB，过点D 作DE⊥BC， 垂足为点E. （1）求证：DE 为⊙O 的切线； （2）求证：DB2=AB·BE. 8.如图，在正方形ABCD 中，对角线AC、BD 相交于点O，E、F 分别在OD、OC 上，且 DE=CF，连接DF、AE，AE 的延长线交DF于点M. 求证：AM⊥DF. 9．（2012 重庆）已知：如图，在菱形 ABCD 中，F 为边 BC 的中点，DF 与对角线 AC 交于点 M，过 M 作 ME⊥CD 于点 E，∠1=∠2． （1）若 CE=1，求 BC 的长； （2）求证：AM=DF+ME． 考点：菱形的性质；全等三角形的判定与性质。 解答：（1）解：∵四边形 ABCD 是菱形， ∴AB∥CD， ∴∠1=∠ACD， ∵∠1=∠2， ∴∠ACD=∠2， ∴MC=MD， ∵ME⊥CD， ∴CD=2CE， ∵CE=1， ∴CD=2， ∴BC=CD =2； （2）证明：如图，∵F 为边 BC 的中点， ∴BF=CF= BC， ∴CF=CE， 在菱形 ABCD 中，AC 平分∠BCD， ∴∠ACB=∠ACD， 在△CEM 和△CFM 中， ∵ ， ∴△CEM≌△CFM（SAS）， ∴ME=MF， 延长 AB 交 DF 于点 G， ∵AB∥CD， ∴∠G=∠2， ∵∠1=∠2， ∴∠1=∠G， ∴AM=MG， 在△CDF 和△BGF 中， ∵ ， ∴△CDF≌△BGF（AAS）， ∴GF=DF， 由图形可知，GM=GF+MF， ∴AM=DF+ME． 10．如图，在梯形 ABCD 中，AD∥BC，AB=CD，分别以 AB，CD 为边向外侧作等边三角形 ABE 和 等边三角形 DCF，连结 AF，DE。 （1）求证：AF=DE； （2）若∠BAD=45°，AB= ，△ABE 和△DCF 的面积之和等 于梯形 ABCD 的面积，求 BC 的长。 解：（1）在梯形 中，AD//BC， ， 而在正 和正 中， ， 且 且 且 AD 公共 ； （2）如图作 ， ，则有 ， a ABCD AB CD= BAD CDA∴∠ = ∠ ABE∆ DCF∆ AB AE= DC DF= 60BAE CDF∠ = ∠ =  AE DF∴ = EAD FDA∠ = ∠ ( )AED DFA SAS∴∆ ≅ ∆ AF DE∴ = BH AD⊥ CK AD⊥ BC HK= 45HAB KDC∠ = ∠ =  2 2AB BH AH∴ = = 同理 而 而由题得 11．如图，△ABC 和△DEF 是两个全等的等腰直角三角形，∠BAC=∠EDF=90°，△DEF 的顶点 E 与△ABC 的斜边 BC 的中点重合．将△DEF 绕点 E 旋转，旋转过程中，线段 DE 与线段 AB 相交于点 P，线段 EF 与 射线 CA 相交于点 Q． （1）如图①，当点 Q 在线段 AC 上，且 AP=AQ 时，求证：△BPE≌△CQE； （2）如图②，当点 Q 在线段 CA 的延长线上时，求证：△BPE∽△CEQ；并求当 BP= ，CQ= 时， P、Q 两点间的距离 (用含 的代数式表示)． a 9 2 a a 2 2CD CK KD= = ( )= 2 AD BC HBS + ⋅ 梯 AB a= 2 2 2( 2 2 ) 22 2= 2 2 a BC a a aBCS × + ⋅ +∴ =梯 23 4AEB DCFS S a∆ ∆= = AEB DCFS S S∆ ∆+ = 梯 2 23 224 2 a aBCa +∴ × = 6 2 2BC a −∴ = 12．如图，在梯形 ABCD 中，AD//BC，AB＝DC，过点 D 作 DE⊥BC，垂足为 E，并延长 DE 至 F，使 EF＝DE．联结 BF、CD、AC． （1）求证：四边形 ABFC 是平行四边形； （2）如果 DE2＝BE·CE，求证四边形 ABFC 是矩形． [解] (1) 等腰梯形 ABCD 中，AB=DC，∠B=∠DCB，∵ △DFC 是等腰三角形，∴ ∠DCB=∠FCE， DC=CF，所以∠B=∠FCE，AB=CF，易证四边形 ABFC 是平行四边形。 (2) 提示：射影定理的逆定理不能直接在中考中使用，必须通过相似三角形来证明，内角为 90°。 A B D F CE , 45 , 45 , 45 135 45 135 45 ABC AB AC ABC ACB E BC BE CE AB AC ABC ACB BE CE DEF DEF BEP CEQ QCE CQE CEQ BEP CQE B QCE BPE CE ° ° ° ° ° ° ° ∆ ∴ = ∠ = ∠ = ∴ = ∆ ∆ = ∠ = ∠ = = ∴∆ ≅ ∆ ∆ ∴∠ = ∴∠ + ∠ = ∠ = ∴∠ + ∠ = ∴∠ = ∠ ∠ = ∠ = ∴∆ ∆∠        ( 1) 解: 为等腰直角三角形 点 为 边中点 在 BPE与 CQE中 BPE CQE ( 2) 证明: 为等腰直角三角形 又 2 29 9 3, , 2 3 22 2 2 9 33 32 2 3 2 3 5, 22 2 Q BP BEBPE CEQ CE CQ BE CE BP a CQ a BE a BE a BC a ABC AB AC a AQ CQ AC a a a AP AB BP a a a PQ Rt APQ AQ a AP a PQ a ∆ ∆∠ ∴ = = = = ∴ = ∴ = ∴ = ∆ ∴ = = ∴ = − = − = = − = − = ∆ = = ∴ =      为等腰直角三角形 连接 在 中 13．如图，AB 是⊙O 的直径，弦 CD⊥AB 于 H，过 CD 延长线上一点 E 作⊙O 的切线交 AB 的延长线 于 F．切点为 G，连接 AG 交 CD 于 K． （1）求证：KE=GE； （2）若 =KD·GE，试判断 AC 与 EF 的位置关系，并说明理由； （3） 在（2）的条件下，若 sinE= ，AK= ，求 FG 的长． 2KG 3 5 2 5 2 2 ( 90 90 CD AB 90 90 (2) : , O BG O FGB BAG O AGB FGB EGK AHK AKH KAH FGB BAG EGK AKH AKH EKG EGK EKG KE GE GD KG KD GE KE GE KG KEKG KD KE KD KG ° ° ° ° ∴∠ =∠ ∴∠ = ∴∠ +∠ = ⊥ ∴∠ = ∴∠ +∠ = ∠ =∠ ∴∠ =∠ ∠ =∠ ∴∠ =∠ ∴ = = = ∴ = ∴ = ∠             (1)证明:连接BG FE为 的切线且 为 的弦 弦切角定理) AB为 的直径 证明 连接 又 3 3sin sin5 5 5 3 ( // (3 5 ,sin 5 4 , , 3 ) EKG GKD EKG GKD KEG KGD KGD ACE ACE CEG AC EF AC CKACK KE E AC CK x Rt ACH AC x CH x AH x G AKC EKG ACK GEK KE GE AC CKGE EK ACE CEG ACE AC K E H =∠ ∴∆ ∆ ∴∠ =∠ ∠ =∠ ∴∠ =∠ ∴ ∠ =∠ ∠ =∠ ∴∆ ∆ ∴ = = ∴ = ∠ =∠ ∠ ∠ = ∴ = = = ∆ = = ∴ = = ∴        同弧所对的圆周角相等) 且 令 在 中 2 2, 2 CD AB 4 5 2 3 5 (3 ) 20 2 5 2, 4 2, 3 2, 2 2 3 2 2 5 5 3 2 CK CH x Rt AKH HK x AK x x x AC CH AH HK DO AH DH ACK DGK ACK DGK CK AKA K DH CK H DGK GKAKC DKG GK DK GK AC AKAC E G K K GEK G = − = ∆ = = ∴ + = ∴ = ∴ = = = = ∴⊥ ∴ = = ∆ ∆ ∠ =∠ ∴∆ ∆ ∴ = ∴ = ∴ =∠ =∠ ∆ ∴ −  = ∆ = =       AB为 的直径CD为弦 在 中AH=3 在 且 与 x, 中 5 2 15 23 15 17 2 2 5 85 17 8 2 5 2 5 2 2 2 2 2 85 15 25 8 4 2 2 2 2 22 8 2 GEK GE ACH HEF AHC E EH EK HK EH GE HK F HF AC CHACH FEH FEFE EH FE G FE GE ∴ = ∴ = ∠ =∠ ∠ =∠ ∴∆ ∆ ∴ = ∴ = ∴ = + ∴ = + = + = ∴ = − = − = =    且