福建省宁德市中考数学试卷含答案解析

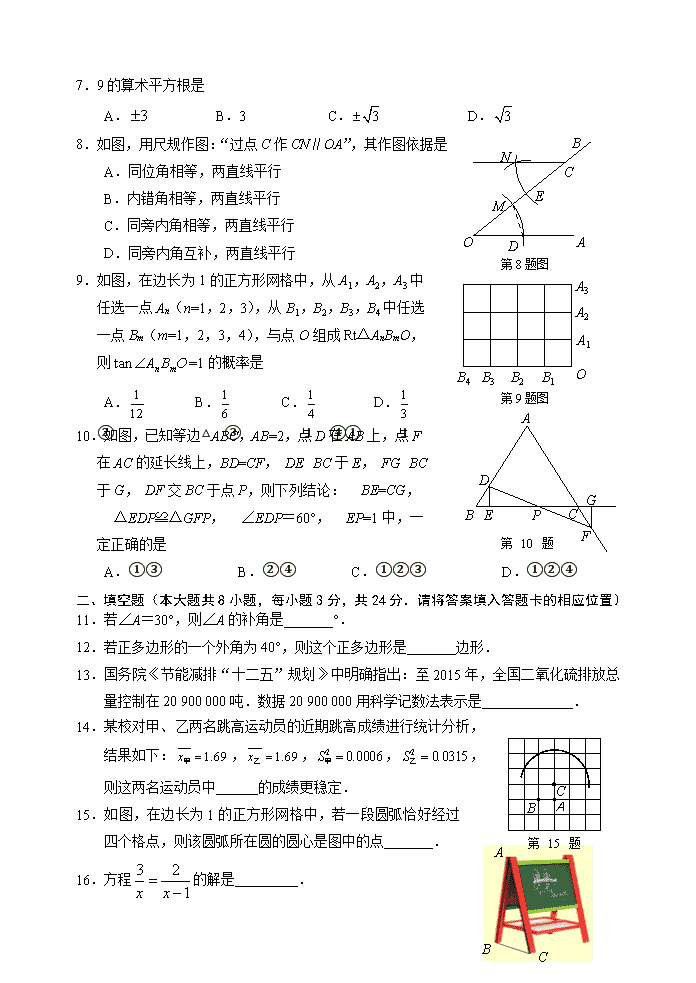
福建省宁德市中考数学试卷含答案解析

‎2014年宁德市中考数学 ‎（满分：150分；考试时间：120分钟）‎ 友情提示：1．所有答案都必须填在答题卡相应的位置上，答在本试卷上一律无效；‎ ‎2．抛物线的顶点坐标是（，）．‎ 一、选择题（本大题共10小题，每小题4分，共40分．每小题只有一个正确的选项，请在答题卡的相应位置填涂）‎ ‎1．-5的相反数是 A． B．- C．-5 D．5‎ ‎2．下列运算正确的是 A． B． ‎ C． D．‎ ‎3．下列图形中，不是正方体表面展开图的是 ‎ A． B． C． D．‎ ‎4．下列事件是必然事件的是 A．任取两个正整数，其和大于1 B．抛掷1枚硬币，落地时正面朝上 C．在足球比赛中，弱队战胜强队 D．小明在本次数学考试中得150分 ‎5．把不等式组的解集表示在数轴上，正确的是 ‎0 1 2 3‎ ‎0 1 2 3‎ ‎0 1 2 3‎ ‎0 1 2 3‎ 第6题图 A M E D B C ‎ A． B． C． D．‎ ‎6．如图，在△ABC中，D，E分别是边AB，AC的中点，∠B=70°，现将△ADE沿DE翻折，点A的对应点为M，则∠BDM的大小是 A．70° B．40° C．30° D．20° ‎ ‎7．9的算术平方根是 B O A M D N E C A． B．3 C． D．‎ ‎8．如图，用尺规作图：“过点C作CN∥OA”，其作图依据是 A．同位角相等，两直线平行 ‎ B．内错角相等，两直线平行 C．同旁内角相等，两直线平行 ‎ 第8题图 O A1‎ A2‎ A3‎ B1‎ B2‎ B3‎ B4‎ D．同旁内角互补，两直线平行 第9题图 ‎9．如图，在边长为1的正方形网格中，从A1，A2，A3中任选一点An（n=1，2，3），从 B1，B2，B3，B4中任选一点Bm（m=1，2，3，4），与点O组成Rt△AnBmO，则=1的概率是 A D B P F C G E A． B． C． D． ‎ 第10题图 ‎10．如图，已知等边△ABC，AB=2，点D在AB上，点F在AC的延长线上，BD=CF， DE⊥BC于E， FG⊥BC于G， DF交BC于点P，则下列结论：①BE=CG，②△EDP≌△GFP，③∠EDP＝60°，④EP=1中，一定正确的是 A．①③ B．②④ C．①②③ D．①②④‎ 二、填空题（本大题共8小题，每小题3分，共24分．请将答案填入答题卡的相应位置）‎ ‎11．若∠A＝30°，则∠A的补角是_______°．‎ ‎12．若正多边形的一个外角为40°，则这个正多边形是_______边形．‎ ‎13．国务院《节能减排“十二五”规划》中明确指出：至2015年，全国二氧化硫排放总量控制在20 900 000吨．数据20 900 000用科学记数法表示是_____________． ‎ 第15题图 Ａ B C ‎14．某校对甲、乙两名跳高运动员的近期跳高成绩进行统计分析，结果如下：，，，，则这两名运动员中______的成绩更稳定．‎ ‎15．如图，在边长为1的正方形网格中，若一段圆弧恰好经过四个格点，则该圆弧所在圆的圆心是图中的点 ． ‎ B C A ‎16．方程的解是 ．‎ 第17题图 ‎17．如图是一款可折叠的木制宝宝画板．已知AB=AC=67cm，BC=30cm，则∠ABC的大小约为_____°（结果保留到1°）． ‎ B P O x y AB ‎18．如图，P是抛物线在第一象限上的点，过点P分别向轴和轴引垂线，垂足分别为A，B，则四边形OAPB周长的最大值为 ．‎ 第18题图 三、解答题（本大题有8小题，共86分．请在答题卡的相应位置作答）‎ ‎19．（本题满分14分）‎ ‎（1）计算：；‎ ‎（2）计算：． ‎ ‎20．（本题满分8分）‎ 某校在校内为见义勇为基金会开展了一次捐款活动，学生会随机调查了部分学生的捐款金额，绘制了如下统计图1和统计图2，请根据相关信息，解答下列问题：‎ ‎（1）直接写出样本中学生捐款金额的众数和中位数，及统计图1中“15元”部分扇形圆心角的度数；‎ ‎（2）求本次被调查学生的人均捐款金额；‎ ‎（3）若随机调查该校一名学生，估计该生捐款金额不低于20元的概率．‎ 图1‎ 图2‎ ‎10元 ‎32%‎ ‎20元 ‎24%‎ ‎15元 ‎5元 ‎8%‎ ‎30元 ‎16%‎ 学生捐款金额扇形统计图 ‎0‎ ‎4‎ ‎8‎ ‎12‎ ‎16‎ 人数 ‎5元 捐款金额 ‎10元 ‎15元 ‎20元 ‎30元 学生捐款金额条形统计图 ‎4‎ ‎16‎ ‎10‎ ‎12‎ ‎8‎ A B C D E ‎21．（本题满分8分）‎ 如图，在梯形ABCD中，AD∥BC，点E是BC的中点，连接AC，DE，AC=AB，DE∥AB．‎ 求证：四边形AECD是矩形．‎ ‎22．（本题满分10分）‎ 为了鼓励市民节约用电，某市对居民用电实行“阶梯收费”（总电费=第一阶梯电费+第二阶梯电费），规定：用电量不超过200度按第一阶梯电价收费，超过200度的部分按第二阶梯电价收费．以下是张磊家2014年3月和4月所交电费的收据，问该市规定的第一阶梯电价和第二阶梯电价分别为每度多少元？　　　　　　　　　　　　　　　　‎ ‎23．（本题满分10分）‎ ‎ 如图，已知□ABCD，∠B=45°，以AD为直径的⊙O经过点C．‎ A B C D O ‎（1）求证：直线BC是⊙O的切线；‎ ‎（2）若AB=，求图中阴影部分的面积(结果保留π)．‎ ‎.‎ ‎24．（本题满分10分）‎ O y A B x 如图，点A在双曲线（k≠0）上，过点A作AB⊥x轴于点B（1，0），且△AOB的面积为1．‎ ‎（1）求k的值；‎ ‎（2）将△AOB绕点O逆时针旋转90°，得到△A′OB′，请在图中画出△A′OB′，并直接写出点A′，B′的坐标；‎ ‎（3）连接A′B，求直线A′B的表达式．‎ ‎25．（本题满分13分）‎ 如图，在Rt△ABC中，∠BAC=90°，AB=AC，在BC的同侧作任意Rt△DBC，∠BDC=90°．‎ ‎（1）若CD=2BD，M是CD中点（如图1），求证：△ADB≌△AMC；‎ 图1‎ A B C D M O 下面是小明的证明过程，请你将它补充完整：‎ 证明：设AB与CD相交于点O，‎ ‎∵∠BDC=90°，∠BAC=90°，‎ ‎∴∠DOB+∠DBO=∠AOC+∠ACO=90°．‎ ‎∵∠DOB=∠AOC，‎ ‎∴∠DBO=∠ ① ．‎ ‎∵M是DC的中点，‎ ‎∴CM=CD= ② ．‎ 图2‎ A B C D O 又∵AB=AC，‎ ‎∴△ADB≌△AMC．‎ ‎（2）若CD＜BD（如图2），在BD上是否存在一点N，使得△ADN是以ＤN为斜边的等腰直角三角形？若存在，请在图2中确定点N的位置，并加以证明；若不存在，请说明理由；‎ ‎（3）当CD≠BD时，线段AD，BD与CD满足怎样的数量关系？请直接写出．‎ ‎26．（本题满分13分）‎ 如图，已知抛物线与轴交于A，B两点，与轴交于C点．‎ ‎（1）求A，B，C三点坐标及该抛物线的对称轴；‎ ‎（2）若点E在x轴上，点P(x，y）是抛物线在第一象限上的点，△APC≌△APE，求E，P两点坐标；‎ ‎（3）在抛物线对称轴上是否存在点M，使得∠AMC是钝角．若存在，求出点M的纵坐标的取值范围；若不存在，请说明理由．‎ 备用图 l A O x y B C P E A O x y B C ‎2014年宁德市初中毕业班质量检测 数学试题参考答案及评分标准 ‎⑴本解答给出了一种或几种解法供参考，如果考生的解法与本解答不同，可参照本答案的评分标准的精神进行评分．‎ ‎⑵对解答题，当考生的解答在某一步出现错误时，如果后续部分的解答未改变该题的立意，可酌情给分．‎ ‎⑶解答右端所注分数表示考生正确作完该步应得的累加分数．‎ ‎⑷评分只给整数分，选择题和填空题均不给中间分．‎ 一、选择题：（本大题有10小题，每小题4分，满分40分）‎ ‎1．D 2．C 3．A 4．A 5．A 6．B 7．B 8．B 9．C 10．D 二、填空题：（本大题有8小题，每小题3分，满分24分）‎ ‎11．150 12．九 13． 14．甲 ‎15．C 16． 17．77 18．6 ‎ 三、解答题（本大题共8小题，共86分．请在答题卡的相应位置作答）‎ ‎19．（本题满分14分）‎ ‎ （1）解：原式=+4+1 …………6分 ‎ = …………7分 ‎ （2）解：原式= ‎ ‎ …………4分 ‎ …………5分 ‎ …………6分 ‎ …………7分 ‎20．（本题满分8分）‎ ‎（1）众数10元，中位数 15元，圆心角 72° ． …………3分 ‎（2）解法一： …………5分 ‎ =16.2元 ‎ 答：人均捐款金额为16.2元． …………6分 ‎ 解法二： …………5分 ‎ =16.2元 ‎ 答：人均捐款金额为16.2元． …………6分 ‎ （3）P(不低于20元）==．‎ 答：在该校随机调查一个学生捐款金额不低于20元的概率为． …………8分 ‎21．（本题满分8分）‎ A B C D E 证明：∵AD∥BC，DE∥AB，‎ ‎∴四边形ABED是平行四边形． …………2分 ‎∴AD = BE．‎ ‎∵点E是BC的中点，‎ ‎∴EC =BE= AD． …………4分 ‎∴四边形AECD是平行四边形． …………5分 ‎∵AB=AC，点E是BC的中点，‎ ‎∴AE⊥BC，即∠AEC = 90°． …………7分 ‎∴□AECD是矩形． …………8分 ‎（证法2：由四边形ABED是平行四边形得DE=AB=AC，∴□AECD是矩形．）‎ ‎22．（本题满分10分）‎ ‎ 解：设第一阶梯电价每度x元，第二阶梯电价每度y元，由题意可得： ……1分 ‎ ， …………7分 ‎ ‎ 解得． …………9分 ‎ 答：第一阶梯电价每度0.5元，第二阶梯电价每度0.6元． …………10分 ‎23．（本题满分10分）‎ A B C D O 证明：（1）连结OC．‎ ‎ ∵四边形ABCD是平行四边形，‎ ‎ ∴．‎ ‎ ∵OC = OD，‎ ‎ ∴，‎ ‎ ∴． ‎ ‎ （或．） …………3分 ‎ ∵AD∥BC，‎ ‎ ∴，‎ ‎ ∴直线BC是⊙O的切线． …………5分 ‎（2）在Rt△DOC中，CD = AB =，，‎ ‎ ∴OC = CDsin=sin=2， …………7分 ‎ ∴AD =2OC =4．‎ S阴影部分=S□ABCD-S Rt△COD- S扇形AOC ‎ ‎ =4×2-×2×2-‎ ‎ =6-π． ‎ ‎ （或S阴影部分=S梯形AOCB- S扇形AOC．) ‎ 答：阴影部分的面积为（6-π）． …………10分 ‎24．（本题满分10分）‎ ‎（1）解法一：由题意得OB=1，‎ ‎∵，AB⊥x轴，‎ 由，得AB=2，‎ ‎∴点A的坐标为A(1，2) ．‎ 将A代入得，k=2． …………3分 解法二：根据S△AOB =，点A在第一象限，得k=2． …………3分 ‎（2）画图（略）； …………5分 A′(-2，1)，B′(0，1) ． …………7分 ‎（3）设直线A′B的表达式(k)，‎ ‎∵A′(-2，1)，B (1，0) ，‎ ‎∴，解得 ． …………9分 ‎ ∴直线A′B的表达式． …………10分 A B C D O N ‎25．（本题满分13分）‎ ‎（1）证明：①∠ACO（或∠ACM) ；②BD； …………4分 ‎（2）解法一：存在．在BD上截取BN=CD， …………5分 同（1）可证得∠ACD =∠ABN．‎ ‎∵AC=AB，∴△ACD≌△ABN， …………6分 ‎∴AD=AN，∠CAD =∠BAN，‎ ‎∴∠CAD+∠NAC=∠BAN+∠NAC，‎ 即∠DAN =∠BAC=90°． …………8分 ‎∴△AND为等腰直角三角形． …………9分 解法二：存在．过点A作AN⊥AD交BD于点N，则∠DAN=90°，…………5分 同（1）可证得∠ABN=∠ACD．‎ ‎∵∠BAC=90°，‎ ‎∴∠CAD+∠CAN=∠BAN+∠CAN=90°，‎ ‎∴∠BAN=∠CAD． …………7分 ‎∵AB=AC，∴△ABN≌△ACD． …………8分 ‎∴AN=AD，∴△AND为等腰直角三角形． …………9分 ‎（3）①当CD＞BD时，CD=BD+AD； …………11分 A O y B C x ‎②当CD＜BD时，BD=CD+AD． …………13分 ‎26．（本题满分13分）‎ 解：（1）把x=0代入，‎ 得y=8，∴C（0，8）． …………1分 由， ‎ 得x=-6，或x=8．‎ ‎∴点A坐标为（-6，0），点B坐标为（8，0）． …………3分 ‎∴抛物线的对称轴方程是直线x=1． …………4分 ‎ ‎（2）如图1，连接AP交OC于F点，设F（0，t），‎ 图1‎ E A O y B C P F x 连接EF，由题意可得AC=10，‎ ‎∵△APC≌△APE，‎ ‎∴AE=AC=10，AP平分∠CAE．‎ ‎∴OE=10-6=4，点E坐标为（4，0）．……5分 ‎∵AP平分∠CAE，‎ ‎∴由对称性得EF= CF=8-t． ‎ 在Rt△EOF中，，‎ ‎∴，解得t=3． ‎ ‎∴点F坐标为（0，3）． ……7分 设直线AF的表达式(k)，‎ 将点A（-6，0），F（0，3）代入，解得，‎ E A O y B C K P F x 图2‎ ‎∴直线AF的表达式 ．‎ 由，‎ 图3‎ E A O y B C G P F 解得或（不符合题意，舍去）．‎ ‎∴P（5，），E（4，0）． …………10分,‎ 注：解法二：如图2，连CE交AP于K，由AC=AE，AP平分∠CAE得K为CE中点，坐标为（2，4），则可求得直线AP的表达式，以下相同；‎ 图4‎ F P E A O x y B C H 解法三：如图3，过点F作FG⊥AC，由AP平分∠CAE，得AG=AO=6，证△AOC∽△FGC，由，得F（0，3），以下相同；‎ 解法四：如图3，过点F作FG⊥AC，设OF=FG=x，CF=8- x，在Rt△CGF中由勾股定理得F（0，3）以下相同；‎ T D A O x y B C Q l S I J 解法五：如图4，用以上方法求出F（0，3）后，可过点P作PH⊥AB，证△AOF∽△AHP，由，设P为（2y-6，y），代入抛物线得出P（5，），E（4，0）；‎ ‎(3) 解法一：如图5，以AC为直径画⊙I，交对称轴l于S，T，作IQ⊥l于Q，IQ交y轴于J，易得I为（-3，4），‎ ‎∴IQ=4，IS=5； …………11分 在Rt△SIQ中由勾股定理得SQ=4‎ 图5‎ ‎∴S，T的坐标分别为（1，7）和（1，1），……12分 当M介于S1和S2之间时，延长AM交⊙I于L，∠ALC=90°，‎ l 图6‎ N S2‎ D A O y B C S1‎ x ‎∠AMC＞∠ALC，∴∠AMC是钝角，∴1＜n＜7．……13分 注：解法二：如图6，对称轴l交x轴D点，设点S在对称轴l上，且∠ASC=90°，过C作CN⊥l于N，连接SC，AS，则有CN=1，AD=7，设SD=m，则SN=8-m． ………11分 由△ADS∽△SNC，解得：m=1或m=7． ‎ 经检验符合题意，得S1和S2的纵坐标分别为7和1……12分 当M介于S1和S2之间时，∠AMC是钝角，‎ ‎∴当∠AMC是钝角时的取值范围是1＜n＜7． ……13分