- 2021-05-13 发布 |
- 37.5 KB |
- 29页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2012数学中考压轴题训练
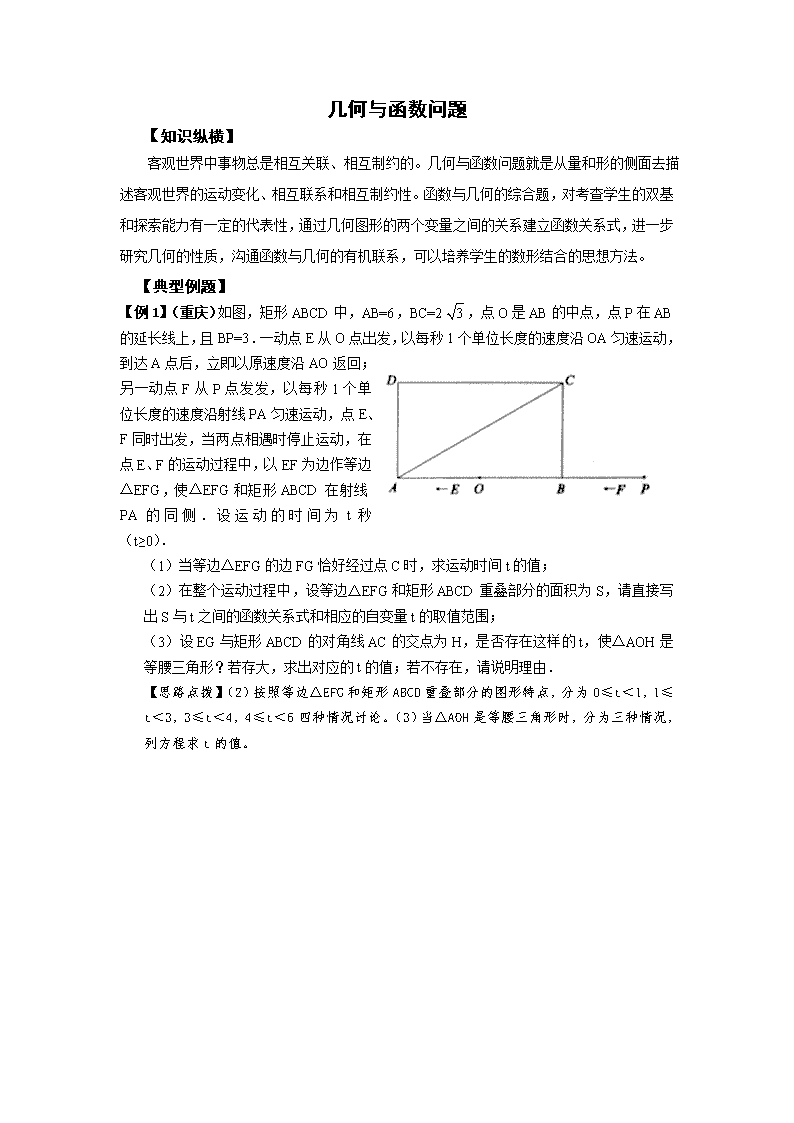
几何与函数问题 【知识纵横】 客观世界中事物总是相互关联、相互制约的。几何与函数问题就是从量和形的侧面去描 述客观世界的运动变化、相互联系和相互制约性。函数与几何的综合题,对考查学生的双基 和探索能力有一定的代表性,通过几何图形的两个变量之间的关系建立函数关系式,进一步 研究几何的性质,沟通函数与几何的有机联系,可以培养学生的数形结合的思想方法。 【典型例题】 【例 1】(重庆)如图,矩形 ABCD 中,AB=6,BC=2 ,点 O 是 AB 的中点,点 P 在 AB 的延长线上,且 BP=3.一动点 E 从 O 点出发,以每秒 1 个单位长度的速度沿 OA 匀速运动, 到达 A 点后,立即以原速度沿 AO 返回; 另一动点 F 从 P 点发发,以每秒 1 个单 位长度的速度沿射线 PA 匀速运动,点 E、 F 同时出发,当两点相遇时停止运动,在 点 E、F 的运动过程中,以 EF 为边作等边 △EFG,使△EFG 和矩形 ABCD 在射线 PA 的 同 侧 . 设 运 动 的 时 间 为 t 秒 (t≥0). (1)当等边△EFG 的边 FG 恰好经过点 C 时,求运动时间 t 的值; (2)在整个运动过程中,设等边△EFG 和矩形 ABCD 重叠部分的面积为 S,请直接写 出 S 与 t 之间的函数关系式和相应的自变量 t 的取值范围; (3)设 EG 与矩形 ABCD 的对角线 AC 的交点为 H,是否存在这样的 t,使△AOH 是 等腰三角形?若存大,求出对应的 t 的值;若不存在,请说明理由. 【思路点拨】(2)按照等边△EFG 和矩形 ABCD 重叠部分的图形特点,分为 0≤t<1,1≤ t<3,3≤t<4,4≤t<6 四种情况讨论。(3)当△AOH 是等腰三角形时,分为三种情况, 列方程求 t 的值。 3 【例 2】(广西梧州)如图,在直角梯形 ABCD 中,AD∥BC,∠B=90°,AD=6cm,AB= 8cm,BC=14cm.动点 P、Q 都从点 C 出发,点 P 沿 C→B 方向做匀速运动,点 Q 沿 C→D→A 方向做匀速运动,当 P、Q 其中一点到达终点时,另一点也随之停止运动. (1)求 CD 的长; (2)若点 P 以 1cm/s 速度运动,点 Q 以 2 2cm/s 的速度运动,连接 BQ、PQ,设△BQP 面积为 S(cm2),点 P、Q 运动的时间为 t(s),求 S 与 t 的函数关系式,并写出 t 的取 值范围; (3)若点 P 的速度仍是 1cm/s,点 Q 的速度为 cm/s,要使在运动过程中出现 PQ∥DC,请你直接写出 的取值范围. 【思路点拨】(1)作辅助线:过 D 点作 DH⊥BC。(2)分 Q 在 CD 和 Q 在 DA 上两种情况讨 论。(3)要使运动过程中出现 PQ∥DC,根据平行四边形判定,只要考虑 QD=PC 即可。 a a 【例 3】(山东青岛)如图,在△ABC 中,AB=AC=10cm,BD⊥AC 于点 D,且 BD= 8cm.点 M 从点 A 出发,沿 AC 的方向匀速运动,速度为 2cm/s;同时直线 PQ 由点 B 出发, 沿 BA 的方向匀速运动,速度为 1cm/s,运动过程中始终保持 PQ∥AC,直线 PQ 交 AB 于 点 P、交 BC 于点 Q、交 BD 于点 F.连接 PM,设运动时间为 ts(0< <5). (1)当 t 为何值时,四边形 PQCM 是平行四边形? (2)设四边形 PQCM 的面积为 ycm2,求 y 与 t 之间的函数关系式; (3)是否存在某一时刻 t,使 S 四边形 PQCM= 9 16S△ABC?若存在,求出 的值;若不存在,说 明理由; (4)连接 PC,是否存在某一时刻 ,使点 M 在线段 PC 的垂直平分线上?若存在,求出 此时 的值;若不存在,说明理由. 【思路点拨】(1) 假设四边形 PQCM 是平行四边形,从而推出结论。(2)把梯形的上下 底和高用 来表示。(3)在假设 S 四边形 PQCM= 9 16S△ABC 的条件下,求出 ,讨论。(4)在假 设点 M 在线段 PC 的垂直平分线上,求出此时 的值。 t t t t t t t 【例 4】(湖南湘潭)已知,AB 是⊙O 的直径,AB=8,点 C 在⊙O 的半径 OA 上运动, PC⊥AB,垂足为 C,PC=5,PT 为⊙O 的切线,切点为 T. (1)如图(1),当 C 点运动到 O 点时,求 PT 的长; (2)如图(2),当 C 点运动到 A 点时,连接 PO、BT,求证:PO∥BT; (3)如图(3),设 PT2= ,AC= ,求 与 的函数关系式及 的最小值. 【思路点拨】(1)连接 OT。(2)连接 AT。(3)连接 OP、OT,应用勾股定理,可得出 与 之间的关系式。 y x y x y y x 几何问题 【知识纵横】 应用几何的判定与性质,解直角三角形的应用和方程思想解决几何问题。 【典型例题】 【例 1】(重庆綦江)如图,等边△ABC 中,AO 是∠BAC 的角平分 线,D 为 AO 上一点,以 CD 为一边且在 CD 下方作等边△CDE,连 接 BE. (1)求证:△ACD≌△BCE; ( 2 )延 长 BE 至 Q , P 为 BQ 上 一 点 , 连 接 CP 、 CQ 使 CP=CQ=5,若 BC=8 时,求 PQ 的长. 【思路点拨】(1)证△ACD≌△BCE。(2)过点 C 作 CH⊥BQ 于 H,求 得∠DAC=30°,再求 PQ 的长。 【例 2】(山东济南)如图,点 C 为线段 AB 上任意一点(不与点 A、B 重合),分别以 AC、BC 为一腰在 AB 的同侧作等腰△ACD 和△BCE, CA=CD,CB=CE,∠ACD 与∠BCE 都是锐 角,且∠ACD=∠BCE,连接 AE 交 CD 于点 M, 连接 BD 交 CE 于点 N,AE 与 BD 交于点 P, 连接 CP. (1)求证:△ACE≌△DCB; (2)请你判断△ACM 与△DPM 的形状有何关系并说明理由; (3)求证:∠APC=∠BPC. 【思路点拨】(3)由(1)可得∠CAE=∠CDB,从而点 A、C、P、D 四点共圆,可得∠APC=∠ ADC,再证明∠BPC=∠BEC,即可。 【例 3】(广东广州)如图 1,⊙O 中 AB 是直径,C 是⊙O 上一点,∠ABC=45°,等腰直 角三角形 DCE 中∠DCE 是直角,点 D 在线段 AC 上. (1)证明:B、C、E 三点 共线; (2)若 M 是线段 BE 的中 点,N 是线段 AD 的中点, 证明:MN= OM; (3)将△DCE 绕点 C 逆时 针旋转 α(0°<α<90°)后, 记为△D1CE1(图 2),若 M1 是线段 BE1 的中点,N1 是线段 AD1 的中点,M1N1= OM1 是否成立?若是,请证明; 若不是,说明理由. 【思路点拨】(1)证明∠BCA+∠DCE=90°+90°= 180°;(2)连接 BD,AE,ON,延长 BD 交 AE 于 F,先 证明 Rt△BCD≌Rt△ACE,再证△ONM 为等腰直角三角 形,即可得到结论。(3)证明的方法和(2)相同。 2 2 【例 4】(上海)在 Rt△ABC 中,∠ACB=90°,BC=30,AB=50.点 P 是 AB 边上任意一 点,直线 PE⊥AB,与边 AC 或 BC 相交于 E.点 M 在线段 AP 上,点 N 在线段 BP 上,EM =EN, . (1)如图 1,当点 E 与点 C 重合时,求 CM 的长; (2)如图 2,当点 E 在边 AC 上时,点 E 不与点 A、C 重合,设 AP= ,BN= ,求 关于 的函数关系式,并写出函数的定义域; (3)若△AME∽△ENB(△AME 的顶点 A、M、E 分别与△ENB 的顶点 E、N、B 对 应),求 AP 的长. 【思路点拨】(2)根据 EM=EN, ,得出△AEP∽△ABC,再求出 。 (3)分点 E 在 AC 上和点 E 在 BC 上两种情况讨论。 12sin EMP 13 ∠ = x y y x 12sin EMP 13 ∠ = PE BC AP AC = 函数及图像与几何问题 【知识纵横】 函数(本节主要指一次函数、反比例函数)及图像与几何问题,是以函数为背景探求 几何性质,这类题很重要点是利用函数的性质,解决几个主要点的坐标问题,使几何知识和 函数知识有机而自然结合起来,这样,才能突破难点。但在解这类题目时,要注意方程的解 与坐标关系,及坐标值与线段长度关系。 【典型例题】 【例 1】(山东济宁)如图,第一象限内半径为 2 的⊙C 与 轴相切于点 A,作直径 AD,过点 D 作⊙C 的切线 l 交 轴于点 B,P 为直线 l 上一动点,已知直线 PA 的解析 式为: =k +3。 (1) 设点 P 的纵坐标为 p,写出 p 随 k 变化的函数关 系式。 (2)设⊙C 与 PA 交于点 M,与 AB 交于点 N,则不论 动点 P 处于直线 l 上(除点 B 以外)的什么位置时,都有△AMN∽△ABP。请你对于点 P 处于图中位置时的两三角形相似给予证明; (3)是否存在使△AMN 的面积等于 的 k 值?若存在,请求出符合的 k 值;若不存在, 请说明理由。 【思路点拨】(1)将 P 的坐标代入 =k +3 即可。(2)要证△AMN∽△ABP,只要证∠ABD ∠AMN 即可。(3)根据(2)的结论,由相似三角形△AMN 和△ABP 的面积比,分点 P 在 B 点上下方两种情况求解。 y x y x 32 25 y x 【例 2】(湖南怀化)在矩形 AOBC 中,OB=6,OA=4,分別以 OB,OA 所在直线为 轴和 轴,建立如图所示的平面直角坐标系.F 是 BC 上的一个动点(不与 B、C 重 合),过 F 点的反比例函数 的图象与 AC 边交于点 E. (1)求证:AE•AO=BF•BO; (2)若点 E 的坐标为(2,4),求经过 O、E、F 三点的抛物线的解析式; (3)是否存在这样的点 F,使得将△CEF 沿 EF 对 折后,C 点恰好落在 OB 上?若存在,求出此时的 OF 的长:若不存在,请说明理由. 【思路点拨】(1)根据反比例函数的性质得出 ,即可得出 AE•AO=BF•BO。 (2)利用 E 点坐标首先求出 BF= ,再利用待定系数法求二次函数解析式即可。 x y ( 0)ky kx = > xy k= 4 3 【例 3】(湖南娄底)在等腰梯形 ABCD 中,AD∥BC,且 AD=2,以 CD 为直径作 ⊙O1,交 BC 于点 E,过点 E 作 EF⊥AB 于 F,建立如图所示的平面直角坐标系,已知 A,B 两点的坐标分别为 A(0,2 ),B(﹣2,0). (1)求 C,D 两点的坐标. (2)求证:EF 为⊙O1 的切线. (3)探究:如图,线段 CD 上是否存在点 P,使得线段 PC 的长度与 P 点到 轴的距离 相等?如果存在,请找出 P 点的坐标;如果不存在,请说明理由. 【思路点拨】(1)连接 DE。(2)连接 O1E,可证 O1E∥AB,再由 EF⊥AB,证明 O1E⊥EF 即可。(3)过 P 作 PM⊥ 轴于 M,作 PN⊥ 轴于 N,再利用锐角三角函数定义求解。 3 y y x 【例 4】(浙江金华、丽水)如图,在平面直角坐标系中,点 A(10,0),以 OA 为直 径在第一象限内作半圆 C,点 B 是该半圆周上一动点,连接 OB、AB,并延长 AB 至点 D, 使 DB=AB,过点 D 作 轴垂线,分别交 轴、直线 OB 于点 E、F,点 E 为垂足,连接 CF. (1)当∠AOB=30°时,求弧 AB 的长度; (2)当 DE=8 时,求线段 EF 的长; (3)在点 B 运动过程中,是否存在以点 E、C、F 为顶点的三角形与△AOB 相似,若存 在,请求出此时点 E 的坐标;若不存在,请说明理由. 【思路点拨】(1)连接 BC。(2)连接 OD,证明△OEF∽△DEA,再利用相似比求 EF。 (3)当以点 E、C、F 为顶点的三角形与△AOB 相似时,分为①当交点 E 在 O,C 之间时,② 当交点 E 在点 C 的右侧时,③当交点 E 在点 O 的左侧时三种情况,分别求出 E 点坐标。 x x 直角坐标下通过几何图形列函数式问题 【知识纵横】 以平面直角坐标系为背景,通过几何图形运动变化中两个变量之间的关系建立函数关 系式,进一步研究几何图形的性质,体现了数形结合的思想方法。但在坐标系中,每一个坐 标由一对的序实数对应,实数的正负之分,而线段长度值均为正的,注意这一点,就可类似 于讲座一的方法解决。所列函数式有:反比例函数、一次函数、二次函数。 【典型例题】 【例 1】(浙江温州)如图,在平面直角坐标系中,O 是坐 标原点,点 A 的坐标是(﹣4,0),点 B 的坐标是(0, ) ( >0).P 是直线 AB 上的一个动点,作 PC⊥ 轴,垂 足为 C.记点 P 关于 y 轴的对称点为 P´(点 P´不在 y 轴 上),连接 PP´,P´A,P´C.设点 P 的横坐标为 . (1)当 =3 时, ①求直线 AB 的解析式; ②若点 P′的坐标是(﹣1, ),求 的值; (2)若点 P 在第一象限,记直线 AB 与 P´C 的交点为 D.当 P´D:DC=1:3 时,求 的值; (3)是否同时存在 , ,使△P´CA 为等腰直角三角形?若存在,请求出所有满足要 求的 , 的值;若不存在,请说明理由. 【思路点拨】(1)①利用待定系数法考虑。②把(﹣1, )代入函数解析式即可。(2) 证明△PP′D∽△ACD,根据相似三角形的对应边的比成比例求解。(3)分 P 在第一,二, 三象限,三种情况进行讨论。 b b x a b m m a a b a b m 【例 2】(浙江舟山、嘉兴)已知直线 ( <0)分别交 轴、 轴于 A、B 两点,线段 OA 上有一动点 P 由原点 O 向点 A 运动,速度为每秒 1 个单位长度,过点 P 作 轴的垂线交直线 AB 于点 C,设运动时间为 秒. (1)当 时,线段 OA 上另有一动点 Q 由点 A 向点 O 运动,它与点 P 以相同速度 同时出发,当点 P 到达点 A 时两点同时停止运动(如图 1). ① 直接写出 =1 秒时 C、Q 两点的坐标; ② 若以 Q、C、A 为顶点的三角形与△AOB 相似,求 的值. (2)当 时,设以 C 为顶点的抛物线 与直线 AB 的另一交点为 D (如图 2), ① 求 CD 的长; ② 设△COD 的 OC 边上的高为 ,当 为何值时, 的值最大? 【思路点拨】(1)②分两种情形讨论。(2)①过点 D 作 DE⊥CP 于点 E,证明△DEC∽△ AOB。 ②先求得三角形 COD 的面积为定值,又由 Rt△PCO∽Rt△OAB,在比例线段中求出 t 值 为多少时,h 最大。 3+= kxy k x y x t 1−=k t t 4 3−=k nmxy ++= 2)( h t h 【例 3】(江苏常州、镇江)在平面直角坐标系 XOY 中,直线 过点 且与 轴 平行,直线 过点 且与 轴平行,直线 与直线 相交于点 P。点 E 为直线 上 一点,反比例函数 ( >0)的图像过点 E 与直线 相交于点 F。 ⑴若点 E 与点 P 重合,求 的值; ⑵连接 OE、OF、EF。若 >2,且△OEF 的面积为△PEF 的面积的 2 倍,求 E 点的坐 标; ⑶是否存在点 E 及 轴上的点 M,使得以点 M、E、F 为顶点的三角形与△PEF 全等? 若存在,求 E 点坐标;若不存在,请说明理由。 【思路点拨】(2)先利用相似三角形对应边的比,用 K 表示相关各点的坐标并表示相关 线段的长,再利用相似三角形 OEF 面积是 PEF 面积 2 倍的关系求出 K。(3)先由全等得到相 似三角形,利用相似三角形对应边的比,用 K 表示相关各点的坐标并表示相关线段的长,再 利用勾股定理求出 K。点 P、E、F 三点位置分 K<2 和 K>2 两种情况讨论。 1l ( )0,1A y 2l ( )2,0B x 1l 2l 2l x ky = k 1l k k y 【例 4】(浙江义乌)已知二次函数的图象经过 A(2,0)、C(0,12) 两点,且对称轴 为直线 x=4. 设顶点为点 P,与 轴的另一交点为点 B. (1)求二次函数的解析式及顶点 P 的坐标; (2)如图 1,在直线 =2 上是否存在点 D,使四边形 OPBD 为等腰梯形?若存在,求 出点 D 的坐标;若不存在,请说明理由; (3)如图 2,点 M 是线段 OP 上的一个动点(O、P 两点除外),以每秒 个单位长度的 速度由点 P 向点 O 运动,过点 M 作直线 MN∥ 轴,交 PB 于点 N. 将△PMN 沿直线 MN 对 折,得到△P1MN. 在动点 M 的运动过程中,设△P1MN 与梯形 OMNB 的重叠部分的面积为 S,运动时间为 t 秒. 求 S 关于 t 的函数关系式. 【思路点拨】(1)利用对称轴公式,A、C 两点坐标,列方程组求 、 、 的值即可。 (2)由(1)可求直线 PB 解析式为 ,可知 PB∥OD,利用 BD=PO,列方程求解, 注意排除平行四边形的情形。(3)分 0<t≤2,2<t<4 两种情形讨论。 x y x 2 x a b c 2 12y x= − 抛物线与几何问题 【知识纵横】 抛物线的解析式有下列三种形式:1、一般式: (a≠0);2、顶点式:y =a(x—h) 2-+k;3、交点式:y=a(x—x 1)(x—x 2 ) ,这里 x 1、x 2 是方程 ax 2 +bx+c=0 的两个 实根。 解函数与几何的综合题,善于求点的坐标,进而求出函数解析式是解题的基础;而充 分发挥形的因素,数形互动,把证明与计算相结合是解题的关键。 【典型例题】 【例 1】(浙江宁波)如图,平面直角坐标 系 中,点 A 的坐标为(-2,2),点 B 的 坐标为(6,6),抛物线经过 A、O、B 三 点,连结 OA、OB、AB,线段 AB 交 轴于 点 E. (1) 求点 E 的坐标; (2) 求抛物线的函数解析式; (3) 点 F 为线段 OB 上的一个动 点(不与点 O、B 重合),直线 EF 与抛物线交于 M、N 两点(点 N 在 轴右侧),连结 ON、BN,当点 F 在线段 OB 上运动时,求△BON 面积的最大值,并求出此时点 N 的坐 标; (4) 连结 AN,当△BON 面积最大时,在坐标平面内求使得△BOP 与△OAN 相似(点 B、O、P 分别与点 O、A、N 对应)的点 P 的坐标. 【思路点拨】(1)根据 A、B 两点坐标求直线 AB 的解析式,令 =0,即可求 E 点坐标。 (2)列方程组求 、 的值。(3)依题意,设 N ,求出△BON 面积关于 的函数表达式,用二次函数的最值原理,可求 N 点的坐标。(4)根据三角形相似的性 质得到 BO:OA=OP:AN=BP:ON,然后根据勾股定理即可求出点 P 的坐标。 2y ax bx c= + + Ox y y y x a b 21 1 , 4 2x x x − x 【例 2】(天津)已知抛物线 : .点 F(1,1). (Ⅰ) 求抛物线 的顶点坐标; (Ⅱ) ①若抛物线 与 轴的交点为 A.连接 AF,并延长交抛物线 于点 B,求证: ②抛物线 上任意一点 P( ))( ).连接 PF.并延长交抛物线 于点 Q( ),试判断 是否成立?请说明理由; (Ⅲ) 将抛物线 作适当的平移.得抛物线 : ,若 时. 恒成立,求 m 的最大值. 【思路点拨】(I) 只要把二次函数变形为 的形式即可。 (II) ①求出 AF 和 BF 即可证明。②应用勾股定理和相似三角形的判定和性质求出 PF 和 QF 即可。(Ⅲ) 应用图象平移和抛物线的性质来证明。 1C 2 1 1 12y x x= − + 1C 1C y 1C 1 1 2AF BF + = 1C P Px y, 0 1Px< < 1C Q Qx y, 1 1 2PF QF + = 1C 2C 2 2 1 ( )2y x h= − 2 x m< ≤ 2y x≤ ( )2y a x m n= − + 【例 3】(浙江省)如图,在直 角坐标系中,抛物线 与 轴交 与点 A(-1,0)、B(3,0)两点,抛 物线交 轴于点 C(0,3),点 D 为 抛物线的顶点.直线 交抛 物线于点 M、N 两点,过线段 MN 上一点 P 作 轴的平行线交抛物 线于点 Q. (1)求此抛物线的解析式及顶点 D 的坐标; (2)问点 P 在何处时,线段 PQ 最长,最长为多少? (3)设 E 为线段 OC 上的三等分点,连接 EP,EQ,若 EP=EQ,求点 P 的坐标. 【思路点拨】(1)由待定系数法可求抛物线的解析式,化为顶点式可求顶点坐标。(2) 把线段 PQ 用含 P( , -1) ,Q ( , )来表示,用二次函数的最值原理 可求。 ( )2 0y ax bx c a= + + ≠ x y 1y x= − y x x x 2 2 3x x− + + 【例 4】(四川成都)如图,在平面直角坐标系 xOy 中,△ABC 的 A、B 两个顶点在 轴上,顶点 C 在 轴的负半轴上.已知|OA|:|OB|=1:5,|OB|=|OC|,△ABC 的面积 S△ABC=15,抛物线 )经过 A、B、C 三点. (1)求此抛物线的函数表达式; (2)设 E 是 轴右侧抛物线上异于点 B 的一个动点,过点 E 作 轴的平行线交抛物线 于另一点 F,过点 F 作 FG 垂直于 轴于点 G,再过点 E 作 EH 垂直于 轴于点 H,得 到矩形 EFGH.则在点 E 的运动过程中,当矩形 EFGH 为正方形时,求出该正方形的边 长; (3)在抛物线上是否存在异于 B、C 的点 M,使△MBC 中 BC 边上的高为 ?若存 在,求出点 M 的坐标;若不存在,请说明理由. 【思路点拨】(1) 由已知设 ,根据题意求 的值。(2)设 E 点坐标为 ,抛物线对称轴为 =2,根据 ,列方程求解。(3)利用直 线解析式与抛物线解析式联立,求 M 点的坐标。 x y 2 ( 0)y ax bx c a= + + ≠ y x x x 7 2 OA ( 0)t t= > t 2( 4 5)x x x− −, x EH EF= 函数、方程、不等式问题 【知识纵横】 函数、方程、不等式的结合,是函数某一变量值一定或在某一范围下的方程或不等式, 体现了一般到特殊的观念。也体现了函数图像与方程、不等式的内在联系,例求两个函数的 交点坐标,一般通过函数解析式组成的方程组来解决。又如例 4 复合了一次函数、二次函数, 并对所得的函数要结合自变量的取值范围来考虑最值,这就需要结合图像来解决。 【典型例题】 【 例 1 】( 四 川 雅 安 ) 如 图 , 已 知 二 次 函 数 图 像 的 顶 点 M 在 反 比 例 函 数 上,且与 轴交于 A,B 两点。 (1)若二次函数的对称轴为 ,试求 的值; (2)在(1)的条件下求 AB 的长; (3)若二次函数的对称轴与 轴的交点为 N,当 NO+MN 取最小值时,试求二次函数 的解析式。 【思路点拨】(1)先求得二次函数 中的 ,再根据顶点在 反比例函数 上,求出 。(3)可用含有 的式子表示点 M、N 的坐标,即求出 的 值,再求得解析式。 cxaxy ++= 22 )0( >a xy 3= x 2 1−=x ca, x cxaxy ++= 22 )0( >a a xy 3= c a a 【例 2】(江苏南通)如图,已知直线 经过点 A(1,0),与双曲线 交于 点 B(2 ,1) .过点 P( , -1)( >1) 作 轴的平行 线分别交双曲线 和 于点 M、 N. (1)求 的值和直线 的解析式; (2)若点 P 在直线 =2 上,求证:△PMB∽△PNA; (3)是否存在实数 ,使得 S△AMN=4S△AMP?若存在,请求出所有满 足条件的 的值;若不存在,请说明理由. 【思路点拨】 (2)先求 的值,再利用对应线段成比例证△PMB∽△PNA。 (3)考虑 点 P 的位置,得 1< <3 时的情况。作延长 MP 交 轴于 Q,先求直线 MP 的方程,再求 出各点坐标(用 表示),然后求出面积表达式,代入 S△AMN=4S△AMP 后求出 值。 l ( )0my x >x = p p p x ( )0my x >x = ( )0my x查看更多