2014湖南省株洲市中考数学

2014湖南省株洲市中考数学

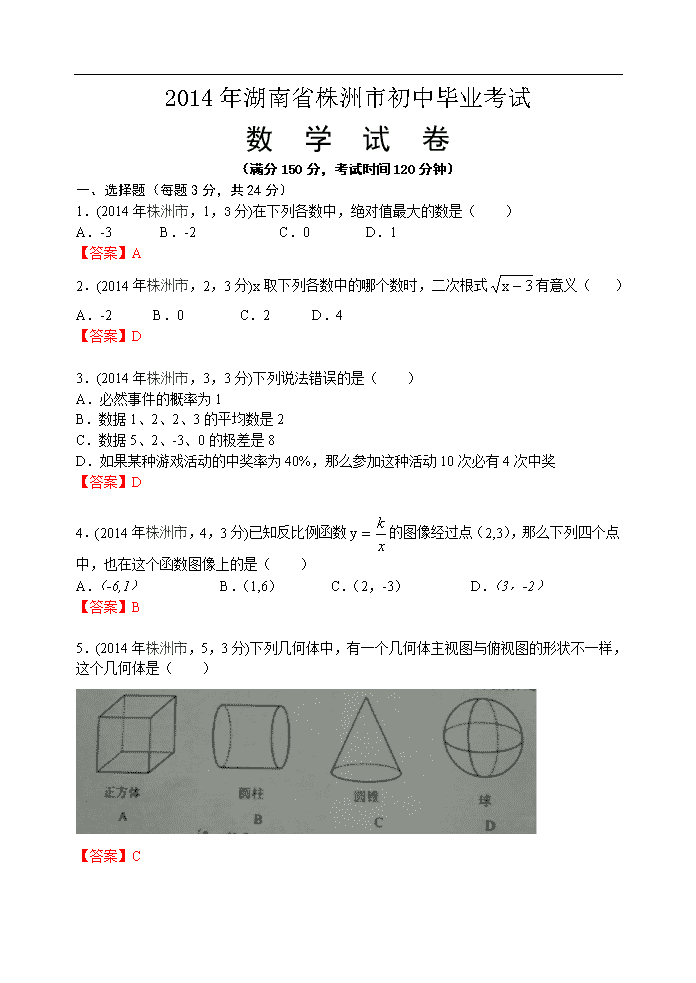
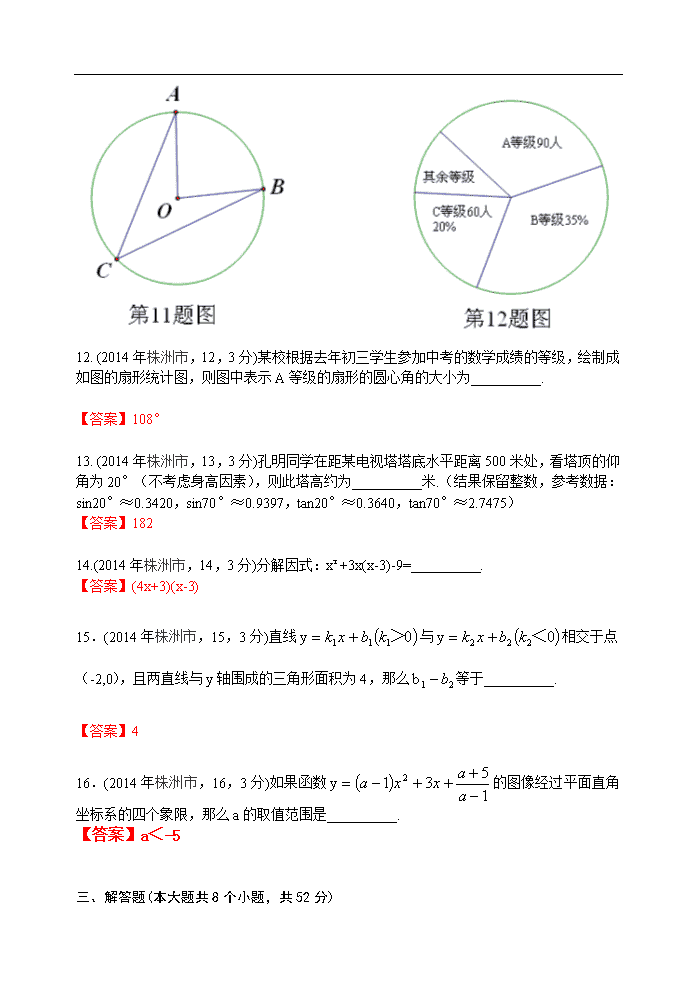
‎2014年湖南省株洲市初中毕业考试 数 学 试 卷 ‎（满分150分，考试时间120分钟）‎ 一、选择题（每题3分，共24分）‎ ‎1．(2014年株洲市，1，3分)在下列各数中，绝对值最大的数是（　　）‎ A．-3 B．-2 C．0 D．1‎ ‎【答案】A ‎2．(2014年株洲市，2，3分)x取下列各数中的哪个数时，二次根式有意义（ ）‎ A．-2 B．0 C．2 D．4‎ ‎【答案】D ‎3．(2014年株洲市，3，3分)下列说法错误的是（　　）‎ A．必然事件的概率为1 ‎ B．数据1、2、2、3的平均数是2 ‎ C．数据5、2、-3、0的极差是8 ‎ D．如果某种游戏活动的中奖率为40%，那么参加这种活动10次必有4次中奖 ‎【答案】D ‎4．(2014年株洲市，4，3分)已知反比例函数的图像经过点（2,3），那么下列四个点中，也在这个函数图像上的是（　　）‎ A．（-6,1） B．（1,6） C．（2，-3） D．（3，-2）‎ ‎【答案】B 5． ‎(2014年株洲市，5，3分)下列几何体中，有一个几何体主视图与俯视图的形状不一样，这个几何体是（　　）‎ ‎【答案】C ‎6．(2014年株洲市，6，3分)一元一次不等式组的解集中，整数解得个数是（　　）‎ A．4 B．5 C．6 D．7‎ ‎【答案】C ‎7．(2014年株洲市，7，3分)已知四边形ABCD是平行四边形，再从①AB=BC，②∠ABC=90°，③AC=BD，④AC⊥BD四个条件中，选两个作为补充条件后，使得四边形ABCD是正方形，现有下列四种选法，其中错误的是（　　）‎ A．选①② B．选②③ C．选①③ D．选②④ ‎ ‎【答案】D ‎8．(2014年株洲市，8，3分)在平面直角坐标系中，孔明做走棋的游戏，其走法是：棋子从原点出发，第1步向右走1个单位，第2步向右走2个单位，第3步向上走1个单位，第4步向右走1个单位……，依此类推，第n步的走法是；当n能被3整除时，则向上走1个单位：当n被3除，余数为1时，则向右走1个单位；当n被3整除，余数为2时，则向右走2个单位。当走完第100步时，棋子所处位置的坐标是（　　）‎ A．（66,34） B．（67,33） C．（100,33） D．（99,34）‎ ‎【答案】C 二、填空题（本题共8小题，每题3分，共24分）‎ ‎9. (2014年株洲市，9，3分)计算：=__________.‎ ‎【答案】‎ ‎10. (2014年株洲市，10，3分)据教育部统计，参加2014年全国高等学校招生考试的学生约为9390000人，用科学计数法表示9390000是__________.‎ ‎【答案】‎ ‎11. (2014年株洲市，11，3分)如图，点A、B、C都在圆O上，如果∠AOB+∠ACB=84°，那么∠ACB的大小是__________.‎ ‎【答案】28°‎ 12. ‎(2014年株洲市，12，3分)某校根据去年初三学生参加中考的数学成绩的等级，绘制成如图的扇形统计图，则图中表示A等级的扇形的圆心角的大小为__________.‎ ‎【答案】108°‎ ‎13. (2014年株洲市，13，3分)孔明同学在距某电视塔塔底水平距离500米处，看塔顶的仰角为20°（不考虑身高因素），则此塔高约为__________米.（结果保留整数，参考数据：sin20°≈0.3420，sin70°≈0.9397，tan20°≈0.3640，tan70°≈2.7475）‎ ‎【答案】182‎ ‎14.(2014年株洲市，14，3分)分解因式：x²+3x(x-3)-9=__________.‎ ‎【答案】(4x+3)(x-3)‎ ‎15．(2014年株洲市，15，3分)直线与相交于点（-2,0），且两直线与y轴围成的三角形面积为4，那么等于__________.‎ ‎【答案】4‎ ‎16．(2014年株洲市，16，3分)如果函数的图像经过平面直角坐标系的四个象限，那么a的取值范围是__________.‎ ‎【答案】a＜-5‎ 三、解答题(本大题共8个小题，共52分)‎ 17. ‎(2014年株洲市，17，4分)计算：‎ ‎【答案】解：原式=4+1-1=4‎ 18. ‎(2014年株洲市，18，4分)先化简，再求值：，其中x=2‎ ‎【答案】解：原式=2(x+1)-3(x-1)=-x+5，当x=2时，原式=3‎ 19. ‎(2014年株洲市，19，6分)我市通过网络投票选出了一批“最有孝心的美少年”，根据各县市区的入选结果制作出如下统计表，后来发现，统计表中前三行的所有数据都是正确的，后三行中有一个数据是错误的，请回答下列问题：‎ ‎（1)统计表中a= ,b= ;‎ ‎ (2)统计表后三行中哪一个数据是错误的？该数据的正确值是多少？‎ （3） 株洲市决定从来自炎陵县的4位“最有孝心的美少年”中，任选两位作为市级形象代言人，A、B是炎陵县“最有孝心的美少年”中的两位，问A、B同时入选的概率是多少？‎ ‎ ‎ 区域 频数 频率 炎陵县 ‎4‎ a 茶陵县 ‎5‎ ‎0.125‎ 攸县 b ‎0.15‎ 醴陵市 ‎8‎ ‎0.2‎ 株洲县 ‎5‎ ‎0.125‎ 株洲市城区 ‎12‎ ‎0.25‎ ‎【答案】解：（1）a=0.1;b=6‎ (2) 最后一个0.25是错误的，正确值应该是0.3‎ (3) ‎20.(2014年株洲市，20，6分)家住山脚下的孔明同学想从家出发登山游玩,据以往的经验，他获得如下信息：‎ ‎（1）他下山时的速度比上山时的速度每小时快1千米；‎ ‎（2）他上山2小时到达的位置，离山顶还有1千米；‎ ‎（3）抄近路下山，下山路程比上山路程近2千米；‎ ‎（4）下山用1个小时；‎ 根据上面信息，他作出如下计划：‎ （1） 在山顶游览1个小时；‎ （2） 中午12：00回到家吃中餐.‎ 若依据以上信息和计划登山游玩，请问：孔明同学应该在什么时间从家出发？‎ ‎ ‎ ‎【答案】解：设上山路程x千米，则下山路程为（x-2)千米，由题意得，‎ ‎∴上山时间：2.5小时；中间游览1小时；下山时间1小时；要在12:00回到家吃中餐，需要12-2.5-1-1=7.5即7:30分从家里出发.‎ 21． ‎(2014年株洲市，21，6分)已知关于x的一元二次方程，其中a、b、c分别为△ABC的三边的长.‎ ‎(1)如果x=-1是方程的根，试判断△ABC的形状，并说明理由；‎ ‎(2)如果方程有两个相等的实数根，试判断△ABC的形状，并说明理由；‎ ‎(3)如果△ABC是等边三角形，试求这个一元二次方程的根.‎ ‎【答案】解：（1）把x=-1代入方程得 ‎2a-2b=0‎ ‎∴a=b ‎∴△ABC是等腰三角形.‎ (2) ‎∵方程有两个相等的实数根 ‎ ∴△=（2b)²-4（a+c)(a-c)=0‎ ‎ ∴b²+c²=a²‎ ‎ ∴△ABC是直角三角形.‎ (3) ‎∵△ABC是等边三角形 ‎ ∴a=b=c ‎ ∴原方程变为：2ax²+2ax=0‎ ‎ ∵a≠0‎ ‎ ∴x1=0;x2=-1‎ ‎22．(2014年株洲市，22，8分)如图，在RT△ABC中，∠C=90°，∠A的平分线交BC于点E，EF⊥AB于点F，点F恰好是AB的一个三等分点（AF＞BF）.‎ （1） 求证：△ACE≌△AFE；‎ （2） 求tan∠CAE的值.‎ ‎ ‎ ‎【答案】(1)证明：∵AE是∠BAC的平分线 ‎ ∴∠CAE=∠FAE；‎ ‎ 又∵∠C=90°‎ ‎ 又∵EF⊥AB ‎ ∴EC=EF;∠EFA=90°‎ ‎ ∴∠C=∠EFA ‎ ∴△ACE≌△AFE（AAS）.‎ (2) 解：∵点F是AB三等分点（AF＞BF）‎ ‎ ∴设BF=1，则AF=2‎ ‎ ∴由（1）得AC=2‎ ‎ 再设CE=2x，则EF=2x ‎ ∵‎ ‎ ∴BE=3x ‎ ∴BC=5x ‎ ∵AC²+BC²=AB²‎ ‎ ∴2²+（5x）²=3²‎ ‎ ∴‎ ‎ ∴‎ ‎ ‎ ‎ ‎ ‎23.(2014年株洲市，23，8分)如图，PQ为圆O的直径，点B在线段PQ的延长线上，OQ=QB=1，动点A在圆O的上半圆运动（含P、Q两点），以线段AB为边向上作等边三角形ABC.‎ ‎（1）当线段AB所在的直线与圆O相切时，求△ABC的面积（图1）；‎ ‎（2）设∠AOB=a，当线段AB与圆O只有一个公共点（即A点）时，求a的范围（图2，直接写出答案）；‎ ‎（3）当线段AB与圆O有两个公共点A、M时，如果AO⊥PM于点N.‎ ‎ 求CM的长度（图3）.‎ ‎ ‎ ‎【答案】解：(1)当AB与圆O相切时，连结AO，过点C作CD⊥AB于D(图4）‎ ‎∵OQ=QB=1‎ ‎∴OA=OQ=1;OB=2‎ ‎∴AB=‎ ‎∵△ABC是等边三角形 ‎∴AD=;CD=‎ ‎∴‎ (2) ‎0°＜a＜60°‎ （3） 连结MQ（图5）‎ ‎ ∵PQ是圆O直径 ‎∴∠PMQ=90°‎ 又∵AO⊥PM ‎∴∠ANM=90°‎ ‎∴∠ANM=∠PMQ ‎∴AO∥MQ ‎∴‎ ‎∵BQ=QO=1‎ ‎∴M为AB中点；AO=1；MQ=0.5；NO=0.25‎ ‎∴AN=0.75；PM=；‎ ‎∴NM=‎ ‎∴AM=‎ ‎∵△ABC是等边三角形 ‎∴CM⊥AB ‎∴CM=‎ ‎24．(2014年株洲市，24，10分)已知抛物线和直线y=(k+1)x+（k+1）².‎ ‎（1）求证：无论k取何实数值，抛物线总与x轴有两个不同的交点；‎ ‎（2）抛物线与x轴交于点A、B，直线与x轴交于点C，设A、B、C三点的横坐标分别是x1、x2、x3，求的最大值；‎ ‎（3）如果抛物线与x轴的交点A、B在原点的右边，直线与x轴的交点C在原点的左边，又抛物线、直线分别交y轴于点D、E，直线AD交直线CE于点G（如图），且，求抛物线的解析式.‎ ‎ ‎ ‎【答案】(1)证明：△=（k+2)²-（5k+2)=k²-k+2=＞0‎ ‎∴无论k取何实数值，抛物线总与x轴有两个不同的交点.‎ (2) 解：∵；‎ ‎ ∴‎ ‎ ∴的最大值是 （3） ‎∵‎ ‎∴AD∥BE ‎∴△OAD∽△OBE ‎∴‎ ‎∴x1=k+1‎ ‎∴k=2‎ ‎∴抛物线解析式为：y=x²-4x+3‎