- 2021-05-13 发布 |
- 37.5 KB |
- 8页

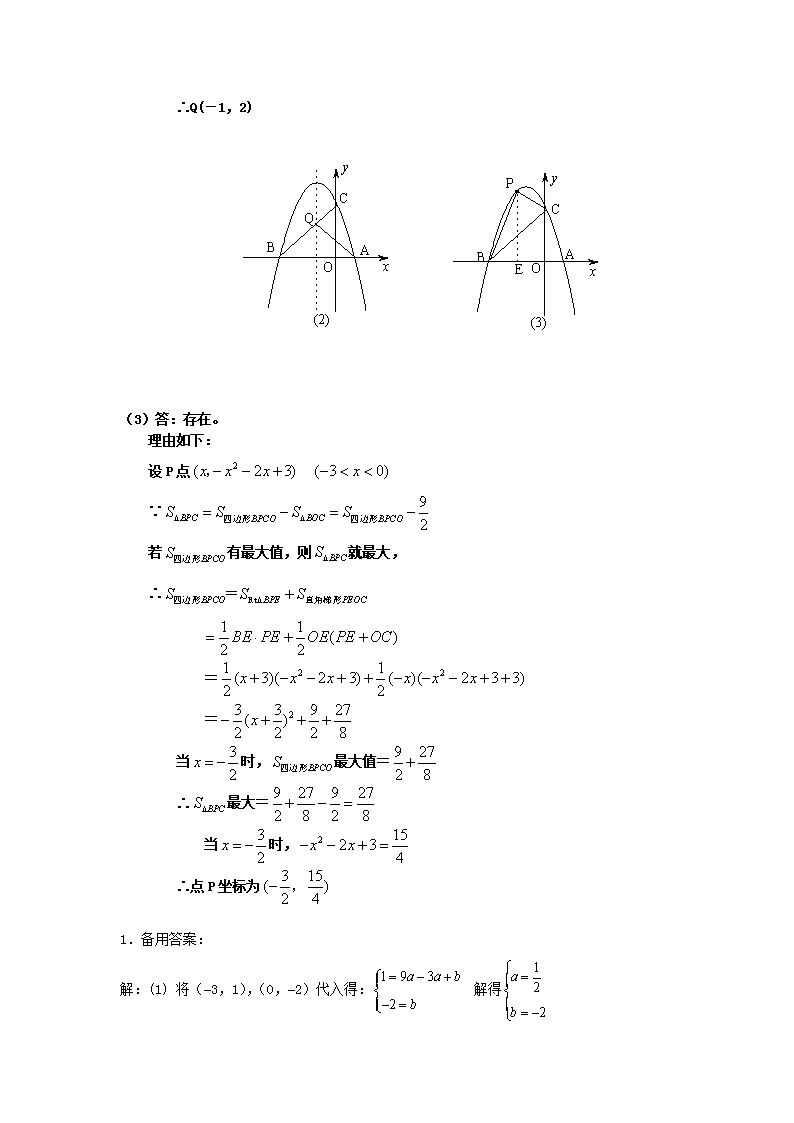

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
中考水平宽铅垂高法求面积最大值带答案
1.如图,抛物线与x轴交与A(1,0),B(- 3,0)两点, (1)求该抛物线的解析式; (2)设(1)中的抛物线交y轴与C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由. (3)在(1)中的抛物线上的第二象限上是否存在一点P,使△PBC的面积最大?,若存在,求出点P的坐标及△PBC的面积最大值.若没有,请说明理由.(12杭州模拟) 解:(1)将A(1,0),B(-3,0)代中得 ∴ ∴抛物线解析式为: (2)存在 理由如下:由题知A、B两点关于抛物线的对称轴对称 ∴直线BC与的交点即为Q点, 此时△AQC周长最小 ∵ ∴C的坐标为:(0,3) 直线BC解析式为: Q点坐标即为的解 1.如图,抛物线与x轴交与A(1,0),B(- 3,0)两点, (1)求该抛物线的解析式; (2)设(1)中的抛物线交y轴与C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由. (3)在(1)中的抛物线上的第二象限上是否存在一点P,使△PBC的面积最大?,若存在,求出点P的坐标及△PBC的面积最大值.若没有,请说明理由.(12杭州模拟) 解:(1)将A(1,0),B(-3,0)代中得 ∴ ∴抛物线解析式为: (2)存在 理由如下:由题知A、B两点关于抛物线的对称轴对称 ∴直线BC与的交点即为Q点, 此时△AQC周长最小 ∵ ∴C的坐标为:(0,3) 直线BC解析式为: Q点坐标即为的解 ∴ ∴Q(-1,2) (3)答:存在。 理由如下: 设P点 ∵ 若有最大值,则就最大, ∴ = = 当时,最大值= ∴最大= 当时, ∴点P坐标为 1.备用答案: 解:(1) 将(–3,1),(0,–2)代入得: ∴ 抛物线的解析式为: (2) 过B作BE⊥x轴于E,则E(–3,0),易证△BEC≌△COA ∴ BE = AO = 2 CO = 1 ∴ C(–1,0) (3) 延长BC到P,使CP = BC,连结AP, 则△ACP为以AC为直角边的等腰直角三角形 过P作PF⊥x轴于F,易证△BEC≌△DFC ∴ CF = CE = 2 PF= BE = 1 ∴ P(1,– 1) 将(1,– 1)代入抛物线的解析式满足 若,AC = AP 则四边形ABCP为平行四边形 过P作PG⊥y轴于G,易证△PGA≌△CEB ∴ PG = 2 AG = 1 ∴ P(2,1)在抛物线上 ∴ 存在P(1,– 1),(2,1)满足条件 2.(本小题满分12分) 如图①, 已知抛物线(a≠0)与轴交于点A(1,0)和点B (-3,0),与y轴交于点C. (1) 求抛物线的解析式; (2) 设抛物线的对称轴与轴交于点N ,问在对称轴上是否存在点P,使△CNP为等腰三角形?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由. (3) 如图②,若点E为第三象限抛物线上一动点,连接BE、CE,求四边形BOCE面积的最大值,并求此时E点的坐标.08 图① 图② (1) 设每年的平均增长率为x,144(1+x)=225,x=1/4 或 x=-9/4 (舍去) (2) 225×(1+1/4)=281 (2) (1) 设可建室内车位个,露天车位b 个, 3a≤b≤4.5a 6000a+2000b=250000 ≤ a≤ (2) a=17,b=74; a=18,b=71; a=19,b=68; a=20,b=65 (4) 24.(本小题满分12分) 如图①, 已知抛物线(a≠0)与轴交于点A(1,0)和点B (-3,0),与y轴交于点C. (1) y=x+2x-3 (2) (2)P(-1,),P(-1,- ),P(-1,-6),P(-1,-) (4) (3) S=1/2×3×(-x-2x+3)+ 1/2×3×(-x) S=-3/2(x+3/2)+63/8 X=-3/2 , S=63/8 (5) E(-3/2,-15/4) (1) 3.(本小题满分12分)(原创) _ M _ A _ B _ O _ x _ y 如图,在平面直角坐标系中,抛物线与直线交于点A、B,M是抛物线上一个动点,连接OM。 (1) 当M为抛物线的顶点时,求△OMB的面积; (2) 当点M在抛物线上,△OMB的面积为10时,求点M的坐标; (3) 当点M在直线AB的下方且在抛物线对称轴的右侧,M运动到何处时,△OMB的面积最大;09 查看更多