中考数学试题与答案

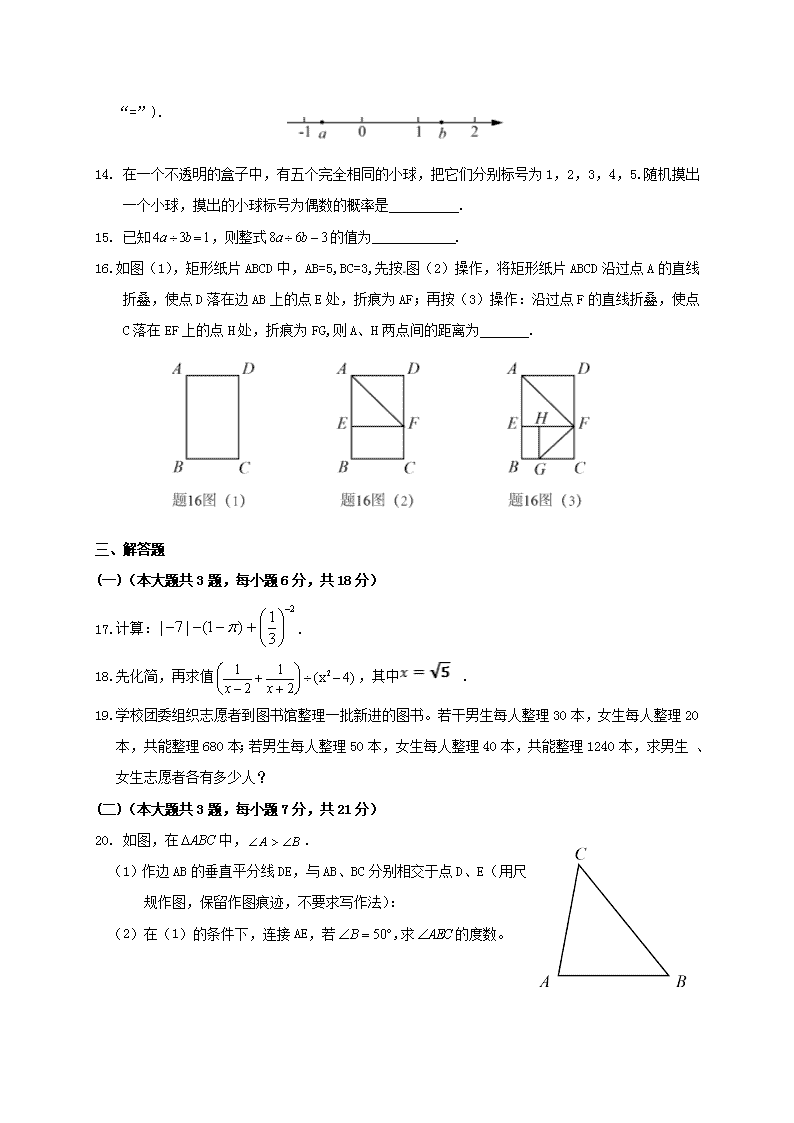
中考数学试题与答案

‎2017年广东、汕头市中考数学试题与答案 ‎ 考试说明：‎ ‎1.全卷共6页，满分为120 分，考试用时为100分钟。‎ ‎2.答卷前，考生务必用黑色字迹的签字笔或钢笔在答题卡填写自己的准考证号、姓名、考场号、座位号。用2B铅笔把对应该号码的标号涂黑。‎ ‎3.选择题每小题选出答案后，用2B铅笔把答题卡上对应题目选项的答案信息点涂黑，如需改动，用橡皮擦干净后，再选涂其他答案，答案不能答在试题上。‎ ‎4.非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再这写上新的答案；不准使用铅笔和涂改液。不按以上要求作答的答案无效。‎ ‎5.考生务必保持答题卡的整洁。考试结束时，将试卷和答题卡一并交回。‎ 一、选择题（本大题10小题，每小题3分，共30分）在每小题列出的四个选项中，只有一个是正确的，请把答题卡上对应题目所选的选项涂黑.‎ ‎1. 5的相反数是( )‎ A. B.5 C.- D.-5‎ ‎2.“一带一路”倡议提出三年以来，广东企业到“一带一路”国家投资越来越活跃.据商务部门发布的数据显示。2016年广东省对沿线国家的实际投资额超过4 000 000 000美元.将4 000 000 000用科学记数法表示为( )‎ A.0.4× B.0.4× C.4× D.4× ‎ ‎3. 已知,则的补角为( )‎ A. B. C. D. ‎ ‎4. 如果2是方程的一个根，则常数k的值为( )‎ A.1 B.2 C.-1 D.-2‎ ‎5. 在学校举行“阳光少年，励志青春”的演讲比赛中，五位评委给选手小明的评分分别为：90，85，90，80，95，则这组的数据的众数是( )‎ A.95 B.90 C.85 D.80‎ ‎6. 下列所述图形中， 既是轴对称图形又是中心对称图形的是( )‎ A.等边三角形 B.平行四边形 C.正五边形 D.圆 ‎7. 如下图，在同一平面直角坐标系中，直线与双曲 线 相交于A、B两点，已知点A的坐标为（1，2），则点B的坐标为( ) ‎ A.（-1，-2） B.（-2，-1） C.（-1，-1） D.（-2，-2）‎ ‎8. 下列运算正确的是( )‎ A. B. C. D. ‎ ‎9. 如下图，四边形ABCD内接于⊙O，DA=DC，∠CBE=50°，则∠DAC的大小为( )‎ A.130° B.100° C.65° D.50°‎ ‎10. 如图，已知正方形ABCD，点E是BC边的中点，DE与AC相交于点F，连接BF，下列结论：①；②；③；④,其中正确的是( )‎ A.①③ B.②③ C.①④ D.②④‎ 二、填空题(本大题6小题，每小题4分，共24分)请将下列各题的正确答案填写在答题卡相应的位置上.‎ ‎11.分解因式： .‎ ‎12.一个n边形的内角和是，那么n= .‎ ‎13.已知实数a,b在数轴上的对应点的位置如题13图所示，则 0(填“>”,“<”或 ‎“=”). ‎ ‎14. 在一个不透明的盒子中，有五个完全相同的小球，把它们分别标号为1，2，3，4，5.随机摸出一个小球，摸出的小球标号为偶数的概率是 .‎ ‎15. 已知，则整式的值为 .‎ ‎16. 如图（1），矩形纸片ABCD中，AB=5,BC=3,先按图（2）操作，将矩形纸片ABCD沿过点A的直线折叠，使点D落在边AB上的点E处，折痕为AF；再按（3）操作：沿过点F的直线折叠，使点C落在EF上的点H处，折痕为FG,则A、H两点间的距离为 . ‎ 三、解答题 ‎(一)（本大题共3题，每小题6分，共18分）‎ ‎17.计算：.‎ ‎18.先化简，再求值，其中.‎ ‎19.学校团委组织志愿者到图书馆整理一批新进的图书。若干男生每人整理30本，女生每人整理20本，共能整理680本；若男生每人整理50本，女生每人整理40本，共能整理1240本，求男生 、女生志愿者各有多少人？‎ ‎(二)（本大题共3题，每小题7分，共21分）‎ ‎20. 如图，在中，.‎ ‎（1）作边AB的垂直平分线DE，与AB、BC分别相交于点D、E（用尺规作图，保留作图痕迹，不要求写作法）：‎ ‎（2）在（1）的条件下，连接AE，若,求的度数。‎ ‎21.如图所示，已知四边形ABCD、ADEF都是菱形，为锐角.‎ ‎（1）求证：;‎ ‎（2）若BF=BC,求的度数。‎ ‎22.某校为了解九年级学生的体重情况，随机抽取了九年级部分学生进行调查，将抽取学生的体重情况绘制如下不完整的统计图表，如题22图表所示，请根据图表信息回答下列问题：‎ （1） 填空：①m= (直接写出结果)；‎ ‎②在扇形统计图中，C组所在扇形的圆心角的度数等于 度；‎ （2） 如果该校九年级有1000名学生，请估算九年级体重低于60千克的学生大约有多少人？‎ ‎(三)（本大题共3题，每小题9分，共27分）‎ ‎23.如图23图，在平面直角坐标系中，抛物线交x轴于A(1,0),B(3,0)两点，点P是抛物线上在第一象限内的一点，直线BP与y轴相交于点C.‎ ‎（1）求抛物线的解析式；‎ ‎（2）当点P是线段BC的中点时，求点P的坐标；‎ ‎（3）在（2）的条件，求的值.‎ ‎24.如图，AB是⊙O的直径，AB=4,点E为线段OB上一点（不与O、B重合），作CE⊥OB，交⊙O于点C，垂足为点E，作直径CD，过点C的切线交DB的延长线于点P，AF⊥PC于点F，连结CB.‎ ‎（1）求证：CB是的平分线；‎ ‎（2）求证：CF=CE;‎ ‎（3）当 时，求劣弧的长度（结果保留π）.‎ ‎25．如图，在平面直角坐标系中，O为原点，四边形ABCO是矩形，点A、C的坐标分别是A(0,1)和C（2,0），点D是对角线AC上一动点（不与A、C重合），连结BD，作DE⊥DB，交x轴于点E，以线段DE、DB为邻边作矩形BDEF.‎ ‎（1）填空：点B的坐标为 ；‎ ‎（2）是否存在这样的点D，使得△DEC是等腰三角形？若存在，请求出AD的长度；若不存在，请说明理由；‎ ‎（3）①求证：；‎ ‎ ②设，矩形BDEF的面积为，求关于的函数关系式（可利用①的结论），并求出的最小值 参考答案 一、 选择题 ‎1.D 2.C 3.A 4.B 5.B 6.D 7.A 8.B 9.C 10.C 二、 填空题 ‎11. a（a+1） 12. 6 13. > 14. 15. -1 16. ‎ 三、 解答题 ‎（一）‎ ‎17. 原式=7-1+3 =9‎ ‎18.解：‎ 当时，上式=‎ ‎19.解：设男生x人，女生y人，则有 答：男生有12人，女生16人。‎ ‎（二）‎ ‎20.（1）作图略 （2） ‎∵ED是AB的垂直平分线 ‎∴EA=EB ‎∴∠EAC=∠B=50°‎ ‎∵∠AEC是△ABE的外角 ‎∴∠AEC=∠EBA+∠B=100°‎ 21、 ‎（1）如图，∵ABCD、ADEF是菱形 ‎∴AB=AD=AF 又∵∠BAD=∠FAD 由等腰三角形的三线合一性质可得 AD⊥BF （2） ‎∵BF=BC ‎∴BF=AB=AF ‎∵△ABF是等比三角形 ‎∴∠BAF=60°‎ 又∵∠BAD=∠FAD ‎∴∠BAD=30°‎ ‎∴∠ADC=180°-30°=150°‎ 22、 ‎（1）①、52‎ ‎（2）144‎ （3） ‎ ‎ 答：略 五、解答题（三）‎ 23、 解（1）把A（1,0）B（3,0）代入得 ‎∴‎ （2） 过P做PM⊥x轴与M ‎∵P为BC的中点，PM∥y轴 ‎∴M为OB的中点 ‎∴P的横坐标为 把x=代入得 ‎∴‎ （3） ‎∵PM∥OC ‎∴∠OCB=∠MPB，‎ ‎∴‎ ‎∴sin∠MPB=‎ ‎∴sin∠OCB=‎ 24、 证明：连接AC，‎ ‎∵AB为直径，‎ ‎∴∠ACB=90°‎ ‎∴∠1+∠2=90°，∠2+∠3=90°‎ ‎∴∠1=∠3‎ 又∵CP为切线 ‎∴∠OCP=90°‎ ‎∵DC为直径 ‎∴∠DBC=90°‎ ‎∴∠4+∠DCB=90°，∠DCB+∠D=90°‎ ‎∴∠4=∠D 又∵弧BC=弧BC ‎∴∠3=∠D ‎∴∠1=∠4即：CB是∠ECP的平分线 （2） ‎∵∠ACB=90°‎ ‎∴∠5+∠4=90°，∠ACE+∠1=90°‎ 由（1）得∠1=∠4‎ ‎∴∠5=∠ACE 在Rt△AFC和Rt△AEC中 ‎∴CF=CE （3） 延长CE交DB于Q ‎25、（1）‎ ‎（2）存在 理由：①如图1 若ED=EC 由题知：∠ECD=∠EDC=30°‎ ‎∵DE⊥DB ‎∴∠BDC=60°‎ ‎∵∠BCD=90°-∠ECD=60°‎ ‎∴△BDC是等边三角形，CD=BD=BC=2‎ ‎∴AC= ‎ ‎∴AD=AC-CD=4-2=2‎ ‎②如图2 若CD=CE 依题意知：∠ACO=30°，∠CDE=∠CED=15°‎ ‎∵DE⊥DB，∠DBE=90°‎ ‎∴∠ADB=180°-∠ADB-∠CDE=75° ‎ ‎∵∠BAC=∠OCA=30° ‎ ‎∴∠ABD=180°-∠ADB-∠BAC=75°‎ ‎∴△ABD是等腰三角形，AD=AB=‎ ‎③：若DC=DE则∠DEC=∠DCE=30°或∠DEC=∠DCE=150°‎ ‎∴∠DEC>90°，不符合题意，舍去 综上所述：AD的值为2或者，△CDE为等腰三角形 ‎ ‎（3）①如图（1），过点D作DG⊥OC于点G，DH⊥BC于点H。‎ ‎ ∵∠GDE + ∠EDH = ∠HDB + ∠EDH = 90°‎ ‎ ∴∠GDE = ∠HDB ‎ 在△ DGE和△ DHB 中，‎ ‎ ‎ ‎∴ ‎ ‎∴ ‎ ‎∵ ‎ ‎∴ ‎ ‎②如图（2），作 ‎ ‎ ‎