中考数学专题圆的切线精华习题

中考数学专题圆的切线精华习题

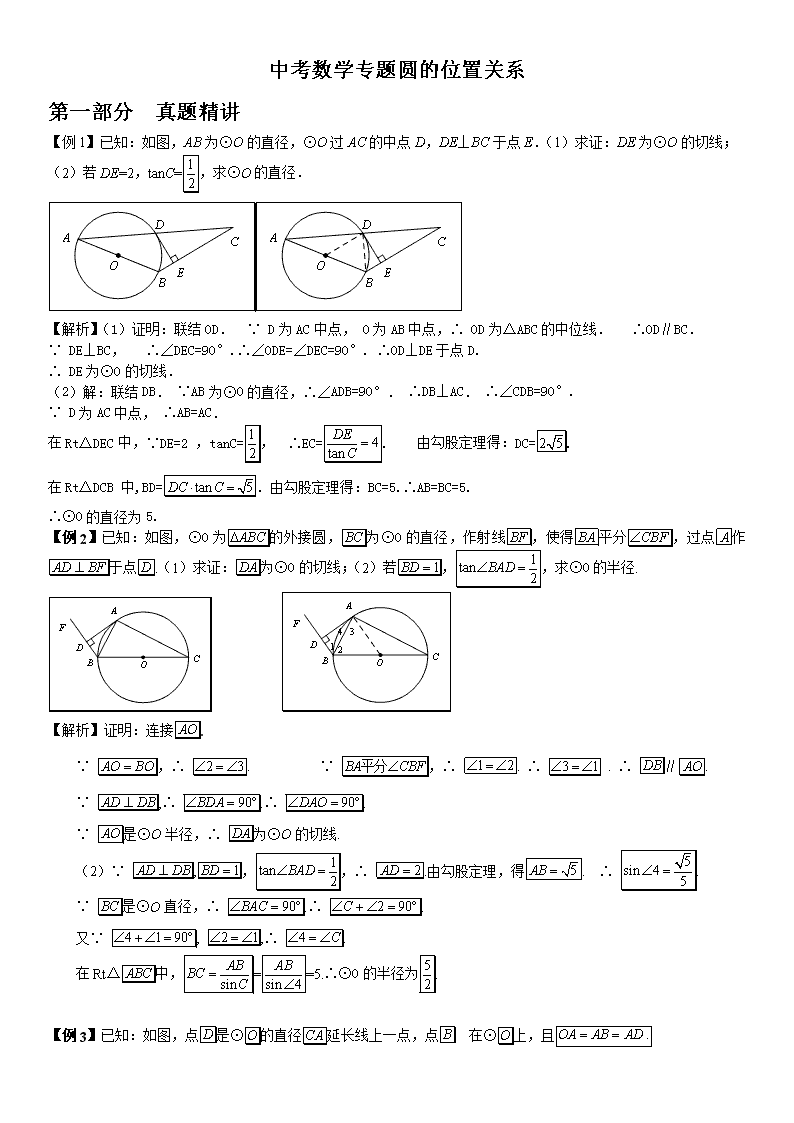
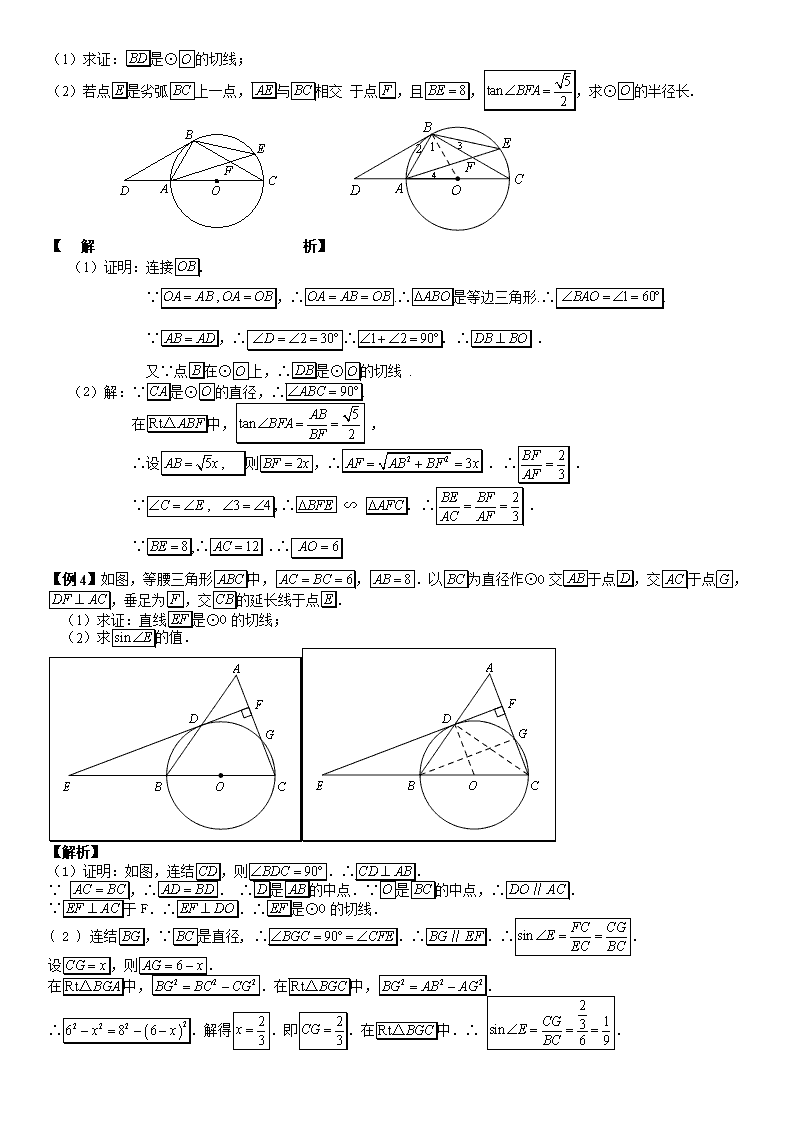
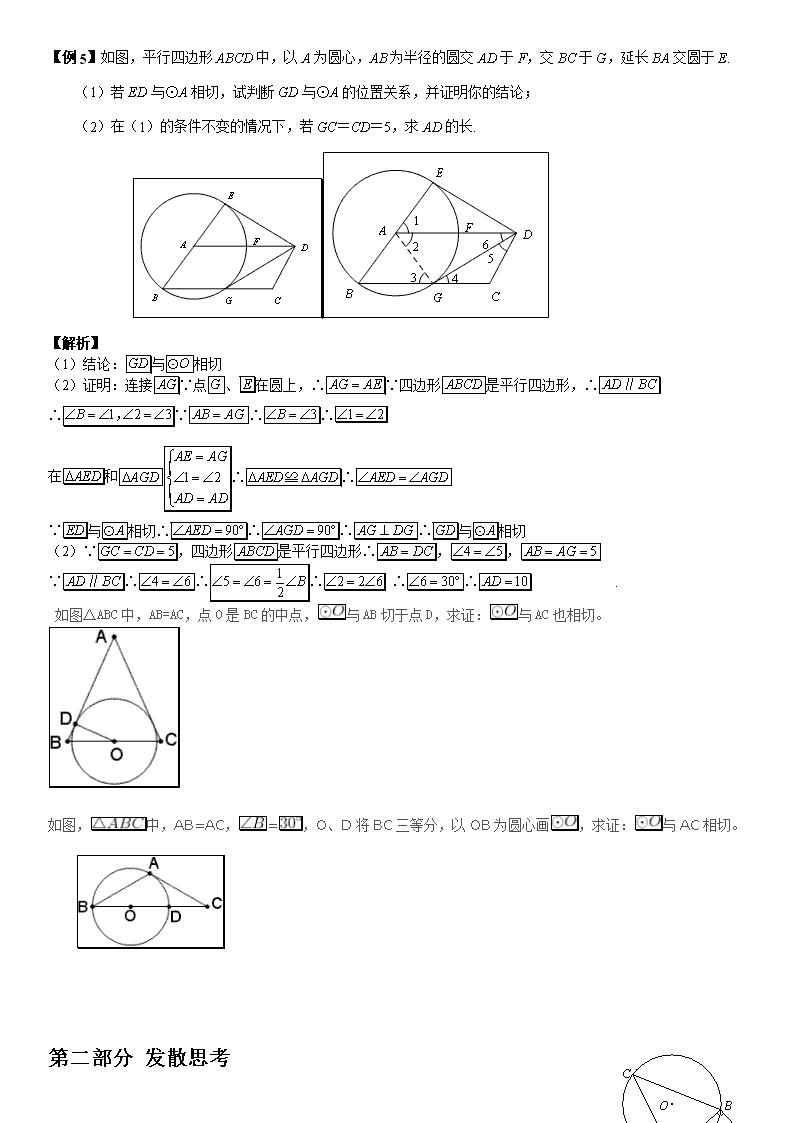
中考数学专题圆的位置关系 第一部分 真题精讲 ‎【例1】已知：如图，AB为⊙O的直径，⊙O过AC的中点D，DE⊥BC于点E．（1）求证：DE为⊙O的切线；‎ ‎（2）若DE=2，tanC=，求⊙O的直径．‎ ‎【解析】（1）证明：联结OD． ∵ D为AC中点， O为AB中点，∴ OD为△ABC的中位线． ∴OD∥BC．‎ ‎∵ DE⊥BC， ∴∠DEC=90°.∴∠ODE=∠DEC=90°. ∴OD⊥DE于点D.‎ ‎∴ DE为⊙O的切线． ‎ ‎（2）解：联结DB． ∵AB为⊙O的直径，∴∠ADB=90°． ∴DB⊥AC． ∴∠CDB=90°. ‎ ‎∵ D为AC中点， ∴AB=AC．‎ 在Rt△DEC中，∵DE=2 ，tanC=， ∴EC=. 由勾股定理得：DC=.‎ 在Rt△DCB 中,BD=．由勾股定理得：BC=5.∴AB=BC=5. ‎ ‎∴⊙O的直径为5. ‎ ‎【例2】已知：如图，⊙O为的外接圆，为⊙O的直径，作射线，使得平分，过点作于点.（1）求证：为⊙O的切线；（2）若，，求⊙O的半径. ‎ ‎ ‎ ‎【解析】证明：连接. ‎ ‎∵ ，∴ . ∵ ，∴ . ∴ . ∴ ∥. ‎ ‎∵ ,∴ .∴ . ‎ ‎∵ 是⊙O半径，∴ 为⊙O的切线. ‎ ‎（2）∵ ,，，∴ .由勾股定理，得. ∴ .‎ ‎∵ 是⊙O直径，∴ .∴ .‎ 又∵ , ,∴ . ‎ 在Rt△中，==5.∴⊙O的半径为. ‎ ‎【例3】已知：如图，点是⊙的直径延长线上一点，点 在⊙上，且 ‎（1）求证：是⊙的切线；‎ ‎（2）若点是劣弧上一点，与相交 于点，且，，求⊙的半径长.‎ ‎【解析】‎ ‎（1）证明：连接.‎ ‎∵，∴.∴是等边三角形.∴.‎ ‎∵，∴∴. ∴ . ‎ 又∵点在⊙上，∴是⊙的切线 . ‎ ‎（2）解：∵是⊙的直径，∴.‎ ‎ 在中， ,‎ ‎ ∴设则，∴ . ∴ . ‎ ‎∵,∴ ∽ . ∴ .‎ ‎∵,∴ .∴‎ ‎【例4】如图，等腰三角形中，，．以为直径作⊙O交于点，交于点，，垂足为，交的延长线于点．‎ ‎（1）求证：直线是⊙O的切线；‎ ‎（2）求的值．‎ ‎【解析】‎ ‎（1）证明：如图，连结，则．∴． ‎ ‎∵ ，∴． ∴是的中点．∵是的中点，∴．‎ ‎∵于F．∴．∴是⊙O的切线． ‎ ‎( 2 ) 连结，∵是直径, ∴．∴．∴．‎ 设，则．‎ 在中，．在中，．‎ ‎∴．解得．即．在中．∴ ．‎ ‎【例5】如图，平行四边形ABCD中，以A为圆心，AB为半径的圆交AD于F，交BC于G，延长BA交圆于E.‎ ‎（1）若ED与⊙A相切，试判断GD与⊙A的位置关系，并证明你的结论；‎ ‎（2）在（1）的条件不变的情况下，若GC＝CD＝5，求AD的长.‎ ‎ ‎ ‎【解析】‎ （1） 结论：与相切 ‎ （2） 证明：连接∵点、在圆上，∴∵四边形是平行四边形，∴‎ ‎∴∵∴∴ ‎ 在和∴∴ ‎ ‎∵与相切∴∴∴∴与相切 ‎ ‎（2）∵，四边形是平行四边形∴，，‎ ‎∵∴∴∴ ∴∴ . ‎ ‎ 如图△ABC中，AB=AC，点O是BC的中点，与AB切于点D，求证：与AC也相切。‎ 如图，中，AB=AC，=，O、D将BC三等分，以OB为圆心画，求证：与AC相切。‎ 第二部分 发散思考 ‎【思考1】如图，已知AB为⊙O的弦，C为⊙O上一点，∠C=∠BAD，且BD⊥AB于B. ‎ ‎（1）求证：AD是⊙O的切线；‎ ‎（2）若⊙O的半径为3，AB=4，求AD的长.‎ ‎【思考2】已知：如图，AB为⊙O的弦，过点O作AB的平行线，交 ‎ ⊙O于点C，直线OC上一点D满足∠D=∠ACB.‎ ‎（1）判断直线BD与⊙O的位置关系，并证明你的结论；‎ ‎（2）若⊙O的半径等于4，，求CD的长.‎ ‎【思考3】已知：如图，在△ABC中，AB=AC,AE是角平分线，BM平分∠ABC交AE于点M,经过B,M两点的⊙O交BC于点G,交AB于点F,FB恰为⊙O的直径.‎ ‎（1）求证：AE与⊙O相切；‎ ‎（2）当BC=4,cosC=时，求⊙O的半径. ‎ ‎【思路分析】这是一道去年北京中考的原题，有些同学可能已经做过了。主要考点还是切线判定，等腰三角形性质以及解直角三角形，也不会很难。放这里的原因是让大家感受一下中考题也无非就是如此出法，和我们前面看到的那些题是一个意思。‎ ‎【思考4】如图，等腰△ABC中，AC=BC，⊙O为△ABC的外接圆，D为上一点， CE⊥AD于E.‎ ‎ 求证：AE= BD +DE．‎ ‎【思路分析】 前面的题目大多是有关切线问题，但是未必所有的圆问题都和切线有关，去年西城区这道模拟题就是无切线问题的代表。此题的关键在于如何在图形中找到和BD相等的量来达到转化的目的。如果图形中所有线段现成的没有，那么就需要自己去截一段，然后去找相似或者全等三角形中的线段关系。‎ ‎【思考5】如图，已知⊙O是△ABC的外接圆，AB是⊙O的直径，D是AB延长线的一点，AE⊥CD交DC的延长线于E，CF⊥AB于F，且CE＝CF．‎ （1） 求证：DE是⊙O的切线；‎ （2） 若AB＝6，BD＝3，求AE和BC的长．‎ ‎【思路分析】又是一道非常典型的用角证平行的题目。题目中虽未给出AC评分角EAD这样的条件，但是通过给定CE=CF，加上有一个公共边，那么很容易发现△EAC和△CAF是全等的。于是问题迎刃而解。第二问中依然要注意找到已知线段的等量线段，并且利用和，差等关系去转化。‎ 第三部分 思考题解析 ‎【思考1解析】‎ ‎1）证明: 如图, 连接AO并延长交⊙O于点E, 连接BE, 则∠ABE=90°.∴ ∠EAB+∠E=90°. ‎ ‎ ∵ ∠E =∠C, ∠C=∠BAD，∴ ∠EAB+∠BAD =90°. ∴ AD是⊙O的切线. ‎ ‎（2）解：由（1）可知∠ABE=90°.‎ ‎∵ AE=2AO=6, AB=4,∴ . ∵ ∠E=∠C=∠BAD, BD⊥AB, ‎ ‎∴ ∴ ∴ . ‎ ‎【思考2解析】‎ 解：（1）直线BD与⊙O相切． ‎ 证明：如图3，连结OB．-‎ ‎∵ ∠OCB=∠CBD +∠D ，∠1=∠D， ∴ ∠2=∠CBD．∵ AB∥OC ，∴ ∠2=∠A ．∴ ∠A=∠CBD．‎ ‎∵ OB=OC，∴ ，∵ ， ∴ ．∴ ．‎ ‎∴ ∠OBD=90°．∴ 直线BD与⊙O相切． ‎ ‎（2）解：∵ ∠D=∠ACB ，，∴ ．‎ 在Rt△OBD中，∠OBD=90°，OB = 4，，∴ ，．∴ ．‎ O B G E C M A F ‎1‎ ‎2‎ ‎3‎ ‎【思考3解析】‎ ‎1）证明：连结，则．∴．∵平分．∴．‎ ‎∴． ∴．∴．‎ 在中，，是角平分线，∴．∴．‎ ‎∴．∴．∴与相切．‎ ‎（2）解：在中，，是角平分线，∴．‎ ‎∵，∴．‎ 在中，，∴．‎ 设的半径为，则．∵，∴．‎ ‎∴．∴．解得．∴的半径为．‎ ‎【思考4解析】‎ 证明：如图3，在AE上截取AF=BD，连结CF、CD． ‎ 在△ACF和△BCD中， ∴ △ACF≌△BCD． ∴ CF=CD. ‎ ‎∵ CE⊥AD于E，∴ EF=DE. ∴ . ‎ ‎【思考5解析】‎ 证明：（1）连接OC,‎ ‎ ‎