中考数学一轮复习 专题练习7 平面几何基础1 浙教版

中考数学一轮复习 专题练习7 平面几何基础1 浙教版

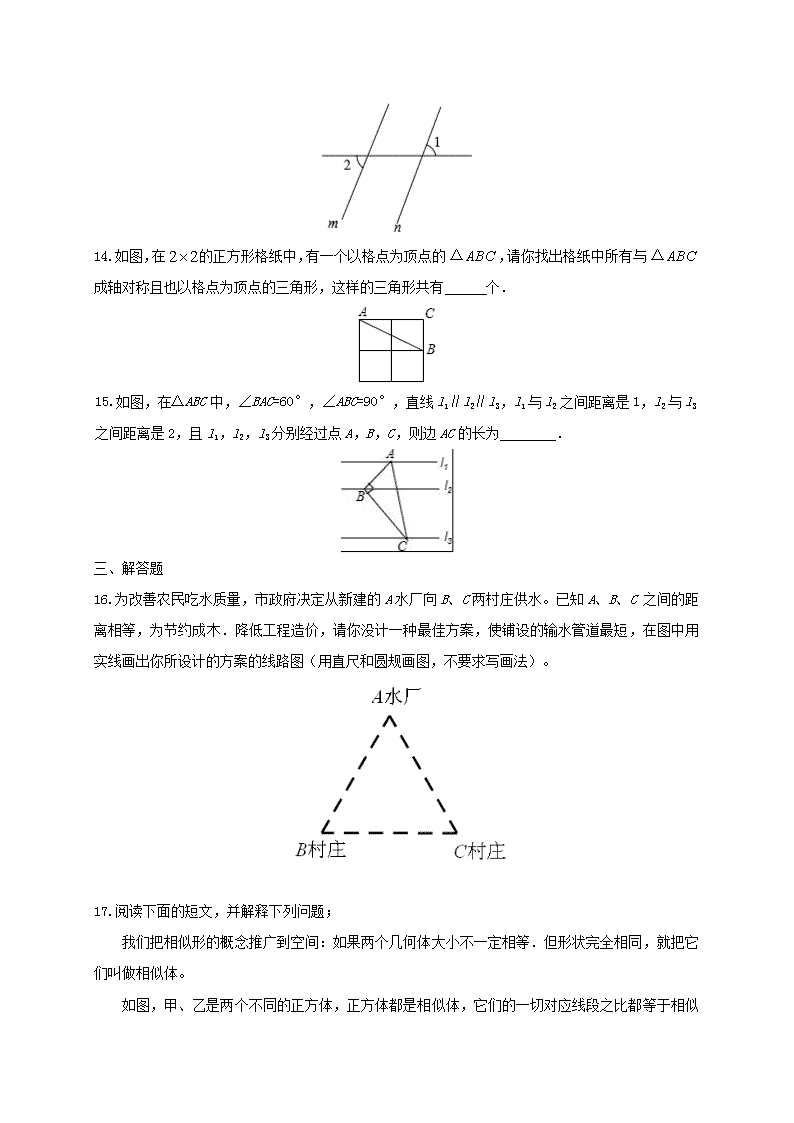
专题复习·平面几何基础（1） 班级 姓名 学号 一、选择题 1.下列命题中，正确的是（ ） A．对顶角相等 B．同位角相等 C．内错角相等 D．同旁内角互补 2.下列命题中，错误的是（ ） A．矩形的对角线互相平分且相等 B．对角线互相垂直的四边形是菱形 C．等腰梯形的两条对角线相等 D．等腰三角形底边上的中点到两腰的距离相等 3.把下列每个字母都看成一个图形，那么中心对成图形有（ ） O L Y M P I C A 1 个 B 2 个 C 3 个 D 4 个 4.等腰三角形一边长为 4，一边长 9，它的周长是（ ） A、17 B、22 C、17 或 22 D、13 5.下列图形中是中心对称图形的是（ ） A、 B、 C、 D、 6.如图，AB∥CD，若∠2=135°，那么∠l 的度数是（ ）． A. 30° B. 45° C. 60° D. 75° 7.△ABC 中，AB=3，BC=4，则 AC 边的长满足（ ） A．AC=5 B．AC  1 C．AC  7 D. 1  AC  7 8.下列由正三角形和正方形拼成的图形中是轴对称图形而不是中心对称图形的是（ ） 9.给出下列四个命题： （1）如果某圆锥的侧面展开图是半圆，则其轴截面一定是等边三角形； （2）若点 A 在直线 y=2x—3 上，且点 A 到两坐标轴的距离相等，则点 A 在第一或第四象限； （3）半径为 5 的圆中,弦 AB=8,则圆周上到直线 AB 的距离为 2 的点共有四个； （4）若 A（a，m）、B（a－1，n）(a  0)在反比例函数 xy 4 的图象上，则 m  n. 其中,正确命题的个数是（ ） A. 1 个 B. 2 个 C. 3 个 D. 4 个 10.下列四个命题中，正确的命题有（ ） ①三角形中至少有一个角不小于 60 度. ②用边长相等的正五边形与正六边形的组合能镶嵌成一个平面. ③如果 4a ，那么不等式 axa  4)4( 的解集是 1x . ④Rt△ABC 中，∠C＝90°,AC＝3,BC＝4，如果以点 C 为圆心，r 为半径的圆与 AB 只有一个公共 点，那么 r ＝ 5 12 . A．1 个 B．2 个 C．3 个 D．4 个 二、填空题 11.如图，两条直线 a，b 被第三条直线 c 所截，如果 a∥b，∠1=70°，那么∠2= 度． 12.在平坦的草地上有 A、B、C 三个小球，若已知 A 球和 B 球相距 3 米，A 球与 C 球相距 1 米，则 B 球与 C 球可能相距 _米。（球的半径忽略不计，只要求填出一个符合条件的数） 13.如图，∠1=700，若 m∥n，则∠2= 14.如图，在 2 2 的正方形格纸中，有一个以格点为顶点的 ABC△ ，请你找出格纸中所有与 ABC△ 成轴对称且也以格点为顶点的三角形，这样的三角形共有 个． 15.如图，在△ABC 中，∠BAC=60°，∠ABC=90°，直线 l1∥l2∥l3，l1 与 l2 之间距离是 1，l2 与 l3 之间距离是 2，且 l1，l2，l3 分别经过点 A，B，C，则边 AC 的长为 ． 三、解答题 16.为改善农民吃水质量，市政府决定从新建的 A 水厂向 B、C 两村庄供水。已知 A、B、C 之间的距 离相等，为节约成木．降低工程造价，请你没计一种最佳方案．．．．，使铺设的输水管道最短，在图中用 实线．．画出你所设计的方案的线路图（用直尺和圆规画图，不要求写画法）。 17.阅读下面的短文，并解释下列问题； 我们把相似形的概念推广到空间：如果两个几何体大小不一定相等．但形状完全相同，就把它 们叫做相似体。 如图，甲、乙是两个不同的正方体，正方体都是相似体，它们的一切对应线段之比都等于相似 比（a：b）。 设 S S乙甲、 分别表示这两个正方体的表面积，则 22 2 S 6a a= =S b6b      甲 乙 。又设 V V乙甲、 分别表示这 两个正方体的体积，则 33 3 V a a= =V bb      甲 乙 。 （1）下列几何体中。一定属于相似体的是（ ） A.两个球体 B. 两个圆锥体 C. 两个圆柱体 D. 两个长方体 （2）请归纳出相似体的三条主要性质：①相似体的一切对应线段（或弧）长的比等于 ；② 相似体表面积的比等于 ；③相似体体积的比等于 。 （3）假定在完全发育的条件下，不同时期的同一人的人体是相似体。一个小朋友上幼儿园时身高为 1.1 米，体重为 18 千克，到了初三时，身高为 1.65 米，问他的体重是多少？（不考虑不同时期人 体平均密度的变化） 18.用剪刀将形状如图 1 所示的矩形纸片 ABCD 沿着直线 CM 剪成两部分,其中 M 为 AD 的中点.用这两 部分纸片可以拼成一些新图形,例如图 2 中的 Rt△BCE 就是拼成的一个图形. (1) 用这两部分纸片除了可以拼成图 2 中的 Rt△BCE 外,还可以拼成一些四边形.请你试一试,把拼好的四 边形分别画在图 3、图 4 的虚框内. (2)若利用这两部分纸片拼成的 Rt△BCE 是等腰直角三角形,设原矩形纸片中的边 AB 和 BC 的长分 别为 a 厘米、 b 厘米,且 a 、 b 恰好是关于 x 的方程 01)1(2  mxmx 的两个实数根, 试求出原矩形纸片的面积. 19.如图，已知 AB=AC=AD，且 AD∥BC，求证：∠C=2∠D． 20.图①是我们常见的地砖上的图案，其中包含了一种特殊的平面图形﹣正八边形． （1）如图②，AE 是⊙O 的直径，用直尺和圆规作⊙O 的内接正八边形ABCDEFGH（不写作法，保留作 图痕迹）； （2）在（1）的前提下，连接 OD，已知 OA=5，若扇形 OAD（∠AOD＜180°）是一个圆锥的侧面，则 这个圆锥底面圆的半径等于 ． 21.某兴趣小组开展课外活动．如图，A，B 两地相距 12 米，小明从点 A 出发沿 AB 方向匀速前进，2 秒后到达点 D，此时他（CD）在某一灯光下的影长为 AD，继续按原速行走 2 秒到达点 F，此时他在 同一灯光下的影子仍落在其身后，并测得这个影长为 1.2 米，然后他将速度提高到原来的 1.5 倍， 再行走 2 秒到达点 H，此时他（GH）在同一灯光下的影长为 BH（点 C，E，G 在一条直线上）． （1）请在图中画出光源 O 点的位置，并画出他位于点 F 时在这个灯光下的影长 FM（不写画法）； （1）求小明原来的速度． 22.“创意设计”公司员工小王不慎将墨水泼在一张设计图纸上，导致其中部分图形和数据看不清楚 （如图 1 所示）．已知图纸上的图形是某建筑物横断面的示意图，它是以圆O 的半径OC 所在的直 线为对称轴的轴对称图形， A 是OD 与圆O 的交点． （1）请你帮助小王在图 2 中把图形补画完整； （2）由于图纸中圆O 的半径 r 的值已看不清楚，根据上述信息（图纸中 1:0.75i  是坡面CE 的坡 度），求 r 的值． 23.如图，点 A 是⊙O 上一点，OA⊥AB，且 OA=1，AB= ，OB 交⊙O 于点 D，作 AC⊥OB，垂足为 M， 并交⊙O 于点 C，连接 BC． （1）求证：BC 是⊙O 的切线； （2）过点 B 作 BP⊥OB，交 OA 的延长线于点 P，连接 PD，求 sin∠BPD 的值． 24.如图，四边形 ABCD 内接于⊙O，AB 是⊙O 的直径，AC 和 BD 相交于点 E，且 DC2=CE•CA． （1）求证：BC=CD； （2）分别延长 AB，DC 交于点 P，过点 A 作 AF⊥CD 交 CD 的延长线于点 F，若 PB=OB，CD= ，求 DF 的长． 答案详解 一、选择题 【考点】 命题和定理，矩形、等腰梯形、等腰三角形的性质，菱形的判定。 【分析】根据矩形、等腰梯形、等腰三角形的性质，菱形的判定则逐一计算作出判断： A．矩形的对角线互相平分且相等，正确； B．对角线互相垂直平分的四边形才是菱形，错误； C．等腰梯形的两条对角线相等，正确； D．等腰三角形底边上的中点到两腰的距离相等，正确。 故选 B。 3.把下列每个字母都看成一个图形，那么中心对成图形有（ ） O L Y M P I C A 1 个 B 2 个 C 3 个 D 4 个 【答案】B。 【考点】中心对称图形。 【分析】根据中心对称图形的概念，中心对称图形是图形沿对称中心旋转 180 度后与原图重合。因 此，把所给字母看成一个图形，中心对成图形有 O，I 两个。故选 B。 4.等腰三角形一边长为 4，一边长 9，它的周长是（ ） A、17 B、22 C、17 或 22 D、13 【答案】B。 【考点】等腰三角形的性质，三角形的构成条件。 【分析】分底边是 4 和底边是两种情况讨论： 当底边是 4 时：三边是 4，9，9，则周长是 22； 当底边是 9 时：三边是：4，4，9，因为 4+4＜9 不能构成三角形。 ∴等腰三角形的周长为 22。故选 B。 5.下列图形中是中心对称图形的是（ ） A、 B、 C、 D、 【答案】C。 【考点】中心对称图形， 【分析】根据中心对称图形是图形沿对称中心旋转 180 度后与原图重合的概念和各图形的特点即可 求解： A、是轴对称图形； B、有五个角，但有旋转，所以既不是轴对称图形也不是中心对称图形； C、即是轴对称图形，又是中心对称图形； D、是轴对称图形。 故选 C。 6.如图，AB∥CD，若∠2=135°，那么∠l 的度数是（ ）． A. 30° B. 45° C. 60° D. 75° 【答案】B。 【考点】平角的定义，平行的性质。 【分析】如图，∵AB∥CD，若∠2=135°， ∴∠3=135°。 ∵∠1＋∠3=1800， ∴∠l=1800－1350=450。故选 B。 7.△ABC 中，AB=3，BC=4，则 AC 边的长满足（ ） A．AC=5 B．AC  1 C．AC  7 D. 1  AC  7 【答案】D。 【考点】三角形三边关系。 【分析】根据三角形的第三边应大于两边之差，而小于两边之和进行分析求解： 根据三角形的三边关系，得 4－3＜AC＜4＋3，即 1＜AC＜7。故选 D。 8.下列由正三角形和正方形拼成的图形中是轴对称图形而不是中心对称图形的是（ ） 【答案】C。 【考点】轴对称图形，中心对称图形。 【分析】根据轴对称图形与中心对称图形的概念，轴对称图形两部分沿对称轴折叠后可重合；中心 对称图形是图形沿对称中心旋转 180 度后与原图重合。因此，A、B、D 都是中心对称也是轴对称图 形，C、是轴对称，但不是中心对称。 故选 C。 9.给出下列四个命题： （1）如果某圆锥的侧面展开图是半圆，则其轴截面一定是等边三角形； （2）若点 A 在直线 y=2x—3 上，且点 A 到两坐标轴的距离相等，则点 A 在第一或第四象限； （3）半径为 5 的圆中,弦 AB=8,则圆周上到直线 AB 的距离为 2 的点共有四个； （4）若 A（a，m）、B（a－1，n）(a  0)在反比例函数 xy 4 的图象上，则 m  n. 其中,正确命题的个数是（ ） A. 1 个 B. 2 个 C. 3 个 D. 4 个 【答案】B。 【考点】几何体的展开图，一次函数图象上点的坐标特征，垂径定理，反比例函数图象上点的坐标 特征。 【分析】根据对称性一一分析得出： （1）如果某圆锥的侧面展开图是半圆，则其轴截面一定是等边三角形，正确； （2）如果点 A 到两坐标轴的距离相等，那么点 A 是 y=x 与 y=2x－3 的交点，是（3，3），在第一象 限，则点 A 在第一或第四象限是正确的； （3）半径为 5 的圆中，弦 AB=8，则圆心距是 3，圆周上到直线 AB 的距离为 2 的点是平行于 AB，弦 心距是 2 的弦与圆的交点．再加上垂直于弦 AB 的半径与圆的交点共 3 个，故其错误； （4）若 A（a，m）、B（a－1，n）（a＞0）在反比例函 4y x  的图象上，而 a 与 a－1 的不能确定是 否同号，即 A，B 不能确定是否在同一象限内，故 m 与 n 的大小关系无法确定．故错误。 故选 B。 10.下列四个命题中，正确的命题有（ ） ①三角形中至少有一个角不小于 60 度. ②用边长相等的正五边形与正六边形的组合能镶嵌成一个平面. ③如果 4a ，那么不等式 axa  4)4( 的解集是 1x . ④Rt△ABC 中，∠C＝90°,AC＝3,BC＝4，如果以点 C 为圆心，r 为半径的圆与 AB 只有一个公共 点，那么 r ＝ 5 12 . A．1 个 B．2 个 C．3 个 D．4 个 【答案】C。 【考点】命题与定理，三角形内角和定理，多边形内角和定理，平面镶嵌（密铺），不等式的性质， 勾股定理，圆与直线的位置关系，切线的性质，相似三角形的判定和性质。 【分析】利用三角形的内角和外角，勾股定理，密铺，切线的性质和不等式的解集等知识分析： ①∵三角形三内角和等于 1800，∴三角形中至少有一个角不小于 60 度。故①正确。 ②∵正五边形的每个内角等于 1080，正六边形的每个内角等于 1200，∴用边长相等的正五边形与正 六边形的组合不能镶嵌成一个平面。故②错误。 ③∵ 4a  ，∴不等式 ( 4) 4a x a   两边同除以正数 4a  得 1x   。故③正确。 ④∵Rt△ABC 中，∠C=90°，AC=3，BC=4，∴AB=5。 ∵以点 C 为圆心， r 为半径的圆与直线 AB 只有一个公共点， ∴圆与直线相切。 设圆与直线的切点为点 D，连接 CD，则 CD 是 AB 的高。 ∴由△ABC∽△ACD 得 CD AC BC BA  ，即 CD 3 4 5  。 ∴ 12=CD= 5r 。故④正确。因此正确的有 3 个答案。 故选 C。 二、填空题 11.如图，两条直线 a，b 被第三条直线 c 所截，如果 a∥b，∠1=70°，那么∠2= 度． 【答案】110。 【考点】平行线的性质。 【分析】根据两直线平行，同旁内角互补得： 已知 a∥b，∠1=70°，则∠2=180°－∠1=110°。 12.在平坦的草地上有 A、B、C 三个小球，若已知 A 球和 B 球相距 3 米，A 球与 C 球相距 1 米，则 B 球与 C 球可能相距 _米。（球的半径忽略不计，只要求填出一个符合条件的数） 【答案】3（答案不唯一）。 【考点】开放型，三角形三边关系，分类思想的应用。 【分析】此题注意两种情况： 当 A，B，C 三个小球共线时，根据线段的和、差计算：BC=2 或 4； 当 A，B，C 三个小球不共线时，根据三角形的三边关系进行分析：2＜BC＜4。 ∴B 球和 C 球可能相距 2 米≤BC≤4 米，如 3 等（答案不惟一只需满足 2 米≤距离≤4 米）。 13.如图，∠1=700，若 m∥n，则∠2= 【答案】700。 【考点】平行的性质，对顶角的性质。 【分析】如图∵m∥n，∠1=700，∴∠3=∠1=700。 又∵∠3 和∠2 是对顶角，∴∠2=∠3=700。 14.如图，在 2 2 的正方形格纸中，有一个以格点为顶点的 ABC△ ，请你找出格纸中所有与 ABC△ 成轴对称且也以格点为顶点的三角形，这样的三角形共有 个． 【答案】5。 【考点】轴对称的性质 【分析】根据轴对称图形的定义与判断可知：与△ABC 成轴对称且也以格点为顶点的三角形有 5 个， 分别为△BCD，△BFH，△ADC，△AEF，△CGH。 15.如图，在△ABC 中，∠BAC=60°，∠ABC=90°，直线 l1∥l2∥l3，l1 与 l2 之间距离是 1，l2 与 l3 之间距离是 2，且 l1，l2，l3 分别经过点 A，B，C，则边 AC 的长为 ． 【答案】 2 213 . 【考点】平行线的性质；锐角三角函数定义；特殊角的三角函数值；相似三角形的判定和性质；勾 股定理． 【分析】如答图，过点 B 作 EF⊥l2，交 l1 于 E，交 l3 于 F， ∵∠BAC=60°，∠ABC=90°，∴ 3BCtan BAC AB    ． ∵直线 l1∥l2∥l3，∴EF⊥l1，EF⊥l3. ∴∠AEB=∠BFC=90°． ∵∠ABC=90°，∴∠EAB=90°﹣∠ABE=∠FBC. ∴△BFC∽△AEB，∴ 3FC BC EB AB   ． ∵EB=1，∴FC= 3 ． 在 Rt△BFC 中，  22 2 22 3 7BC BF FC     ． 在 Rt△ABC 中， 7 2 2133 2 BCAC sin BAC    ． 三、解答题 16.为改善农民吃水质量，市政府决定从新建的 A 水厂向 B、C 两村庄供水。已知 A、B、C 之间的距 离相等，为节约成木．降低工程造价，请你没计一种最佳方案．．．．，使铺设的输水管道最短，在图中用 实线．．画出你所设计的方案的线路图（用直尺和圆规画图，不要求写画法）。 【答案】解：画图如下： 【考点】尺规作图。 【分析】本题是著名的费马点的应用，下面说明点 O 是到 A、B、C 的距离和最短。 ∵△ABC 是等边三角形，点 O 是其重心， ∴∠AOB=∠BOC=∠AOC=120°。 如图，以 AC 为边向右上方作等边三角形△DAC，以 AO 为边向右上方作等边三角形△AOE，连 接 OD。 ∵∠AOD=60°, ∠AOE=60°， ∴O、E、D 三点一线。 ∵∠AOB=120°, ∠AOE=60°， ∴B、O、E 三点一线。 ∴B、O、E、D 共线。 易证△AOB≌△AED（SAS）， ∴BO=DE。 ∴AO＋BO＋OC=BD。 ∴O 点是等边三角形内到三个顶点的距离之和最小的那一点，费马点。也就是重心。 17.阅读下面的短文，并解释下列问题； 我们把相似形的概念推广到空间：如果两个几何体大小不一定相等．但形状完全相同，就把它 们叫做相似体。 如图，甲、乙是两个不同的正方体，正方体都是相似体，它们的一切对应线段之比都等于相似 比（a：b）。 设 S S乙甲、 分别表示这两个正方体的表面积，则 22 2 S 6a a= =S b6b      甲 乙 。又设 V V乙甲、 分别表示这 两个正方体的体积，则 33 3 V a a= =V bb      甲 乙 。 （1）下列几何体中。一定属于相似体的是（ ） A.两个球体 B. 两个圆锥体 C. 两个圆柱体 D. 两个长方体 （2）请归纳出相似体的三条主要性质：①相似体的一切对应线段（或弧）长的比等于 ；② 相似体表面积的比等于 ；③相似体体积的比等于 。 （3）假定在完全发育的条件下，不同时期的同一人的人体是相似体。一个小朋友上幼儿园时身高为 1.1 米，体重为 18 千克，到了初三时，身高为 1.65 米，问他的体重是多少？（不考虑不同时期人 体平均密度的变化） 【答案】（1）A。 （2）①相似比；②相似比的平方；③相似比的立方。 （3）由题意知，他的体积比为 31.1( )1.65 又因为体重之比等于体积比，若设初三时的体重为 xkg，则有 31.1 18( )1.65 x  ，解得，x= 243 =60.754 （千克）。 答：初三时的体重为 60.75 千克。 【考点】阅读型，新定义，相似多边形的性质。 【分析】根据阅读材料可以知道相似体就是形状完全相同的物体，根据体积的计算方法就可以求出 所要求的结论。 18.用剪刀将形状如图 1 所示的矩形纸片 ABCD 沿着直线 CM 剪成两部分,其中 M 为 AD 的中点.用这两 部分纸片可以拼成一些新图形,例如图 2 中的 Rt△BCE 就是拼成的一个图形. (1) 用这两部分纸片除了可以拼成图 2 中的 Rt△BCE 外,还可以拼成一些四边形.请你试一试,把拼好的四 边形分别画在图 3、图 4 的虚框内. (2)若利用这两部分纸片拼成的 Rt△BCE 是等腰直角三角形,设原矩形纸片中的边 AB 和 BC 的长分 别为 a 厘米、 b 厘米,且 a 、 b 恰好是关于 x 的方程 01)1(2  mxmx 的两个实数根, 试求出原矩形纸片的面积. 【答案】解：（1） （2）由题可知 AB＝CD＝AE，又 BC＝BE＝AB＋AE。 ∴BC＝2AB， 即 2b a 。 由题意知 ,2a a 是方程 2 ( 1) 1 0x m x m     的两根， ∴ 2 1 2 1 a a m a a m        。 消去 a 得， 22 13 7 0m m   ，解得， 7m  或 1 2m   。 经检验：∵当 1 2m   ， 32 02a a    ，∴ 1 2m   不符合题意，舍去。 7m  符合题意。 ∴ 1 8S ab m   矩形 。 答：原矩形纸片的面积为 8 平方厘米。 【考点】应用与设计作图，等腰直角三角形的性质，一元二次方程根与系数的关系。 【分析】（1）相等的边为 CD 与 AB；AM=MD 让相等的边重合即可。 （2）根据等腰直角三角形可得到 a 和b 的关系．根据根与系数的关系求得到 7m  ，从而求 出原矩形纸片的面积。 19.如图，已知 AB=AC=AD，且 AD∥BC，求证：∠C=2∠D． 【答案】证明：∵AB=AC=AD，∴∠C=∠ABC，∠D=∠ABD. ∴∠ABC=∠CBD+∠D. ∵AD∥BC，∴∠CBD=∠D. ∴∠ABC=∠D+∠D=2∠D. 又∵∠C=∠ABC，∴∠C=2∠D． 【考点】等腰三角形的性质；平行线的性质． 【分析】首先根据 AB=AC=AD，可得∠ABC=∠CBD+∠D；然后根据 AD∥BC，可得∠CBD=∠D，据此判断 出∠ABC =2∠D.，再根据∠C=∠ABC，即可判断出∠C=2∠D． 20.图①是我们常见的地砖上的图案，其中包含了一种特殊的平面图形﹣正八边形． （1）如图②，AE 是⊙O 的直径，用直尺和圆规作⊙O 的内接正八边形 ABCDEFGH（不写作法，保留作 图痕迹）； （2）在（1）的前提下，连接 OD，已知 OA=5，若扇形 OAD（∠AOD＜180°）是一个圆锥的侧面，则 这个圆锥底面圆的半径等于 ▲ ． 【答案】解：（1）如答图所示，八边形 ABCDEFGH 即为所求， （2）∵八边形 ABCDEFGH 是正八边形，∴ 360 3 1358AOD      . ∵OA=5，∴ » 135 5 15 180 4AD     . 设这个圆锥底面圆的半径为 R， ∴ 152 4R  ，解得 15 8R  ∴这个圆锥底面圆的半径为 15 8 ． 【考点】作图（复杂作图）；正多边形和圆；圆锥和扇形的计算． 【分析】（1）作 AE 的垂直平分线交⊙O 于 C，G，作∠AOG，∠EOG 的角平分线，分别交⊙O 于 H，F， 反向延长 FO，HO，分别交⊙O 于 D，B，顺次连接 A，B，C，D，E，F，G，H，八边形 ABCDEFGH 即为 所求； （2）由八边形 ABCDEFGH 是正八边形，求得 AOD ，根据弧长公式求得得到 »AD 的长，设 这个圆锥底面圆的半径为 R，根据圆锥的底面周长等于它的侧面展开图的弧长列方程即可求得结果． 21.某兴趣小组开展课外活动．如图，A，B 两地相距 12 米，小明从点 A 出发沿 AB 方向匀速前进，2 秒后到达点 D，此时他（CD）在某一灯光下的影长为 AD，继续按原速行走 2 秒到达点 F，此时他在 同一灯光下的影子仍落在其身后，并测得这个影长为 1.2 米，然后他将速度提高到原来的 1.5 倍， 再行走 2 秒到达点 H，此时他（GH）在同一灯光下的影长为 BH（点 C，E，G 在一条直线上）． （1）请在图中画出光源 O 点的位置，并画出他位于点 F 时在这个灯光下的影长 FM（不写画法）； （1）求小明原来的速度． 【答案】解：（1）光源 O 点的位置如图， （2）设小明原来的速度为 xm/s， 则  2 4 1.2 4 1.2CE xm AM AF MF x x m     ， （ ） ，  2 1.5 3 12 4 1.2 13.2 4EG x xm BM AB AM x x         ， ， ∵点 C，E，G 在一条直线上，CG∥AB，∴△OCE∽△OAM，△OEG∽△OMB， ∴ ,CE OE EG OE AM OM BM OM   .∴ CE EG AM BM  ，即 2 3 4 1.2 13.2 4 x x x x   ，解得 x=1.5. 经检验 x=1.5 为方程的解， ∴小明原来的速度为 1.5m/s． 答：小明原来的速度为 1.5m/s． 【考点】中心投影；分式方程的应用；相似三角形的应用． 【分析】（1）利用中心投影的定义画图. （2）设小明原来的速度为 xm/s，用 x 表示出 CE、AM、EG、BM 的长，根据相似三角形的判 定方法得到△OCE∽△OAM，△OEG∽△OMB，则 ,CE OE EG OE AM OM BM OM   ，所以 CE EG AM BM  ，据此列 方程求解即可． 22.“创意设计”公司员工小王不慎将墨水泼在一张设计图纸上，导致其中部分图形和数据看不清楚 （如图 1 所示）．已知图纸上的图形是某建筑物横断面的示意图，它是以圆O 的半径OC 所在的直 线为对称轴的轴对称图形， A 是OD 与圆O 的交点． （1）请你帮助小王在图 2 中把图形补画完整（3 分）； （2）由于图纸中圆O 的半径 r 的值已看不清楚，根据上述信息（图纸中 1:0.75i  是坡面CE 的坡 度），求 r 的值（7 分）． 【答案】解：（1）图形补画如下： （2）由已知OC DE ，垂足为点 H ，则 90CHE   ． ∵ 1:0.75i  ，∴ 4 3 CH EH  。 在 Rt HEC△ 中， 2 2 2EH CH EC  ．设 4CH k ， 3 ( 0)EH k k  ， 又∵ 5CE  ，得 2 2 2(3 ) (4 ) 5k k  ，解得 1k  。∴ 3EH  ， 4CH  。 ∴ 7DH DE EH   ， 7OD OA AD r    ， 4OH OC CH r    。 在 Rt ODH△ 中， 2 2 2OH DH OD  ，∴ 2 2 2( 4) 7 ( 7)r r    ，解得 8 3r  。 23. 如图，点 A 是⊙O 上一点，OA⊥AB，且 OA=1，AB= ，OB 交⊙O 于点 D，作 AC⊥OB，垂足为 M， 并交⊙O 于点 C，连接 BC． （1）求证：BC 是⊙O 的切线； （2）过点 B 作 BP⊥OB，交 OA 的延长线于点 P，连接 PD，求 sin∠BPD 的值． 【解析】（1）证明：连结 OC，如图， ∵AC⊥OB，∴AM=CM， ∴OB 为线段 AC 的垂直平分线，∴BA=BC， 在△OAB 和△OCB 中 24.如图，四边形 ABCD 内接于⊙O，AB 是⊙O 的直径，AC 和 BD 相交于点 E，且 DC2=CE•CA． （1）求证：BC=CD； （2）分别延长 AB，DC 交于点 P，过点 A 作 AF⊥CD 交 CD 的延长线于点 F，若 PB=OB，CD= 22 ，求 DF 的长． 【解析】（1）证明：∵DC2=CE•CA， △CDE∽△CAD， ∴∠CDB=∠DBC， ∵四边形 ABCD 内接于⊙O， ∴BC=CD； （2）解：如图，连接 OC， ∵BC=CD， ∴∠DAC=∠CAB， 又∵AO=CO， ∴∠CAB=∠ACO， ∴∠DAC=∠ACO， ∴AD∥OC，