绍兴市2013年中考数学卷

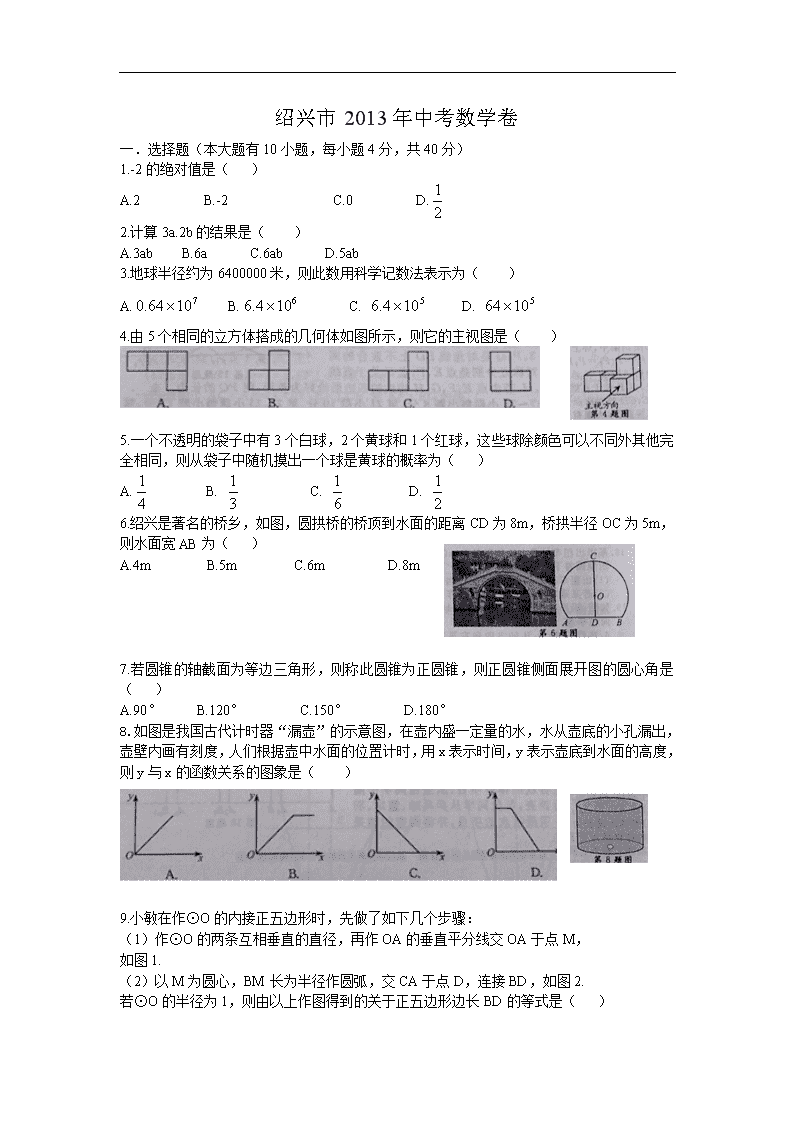
绍兴市2013年中考数学卷

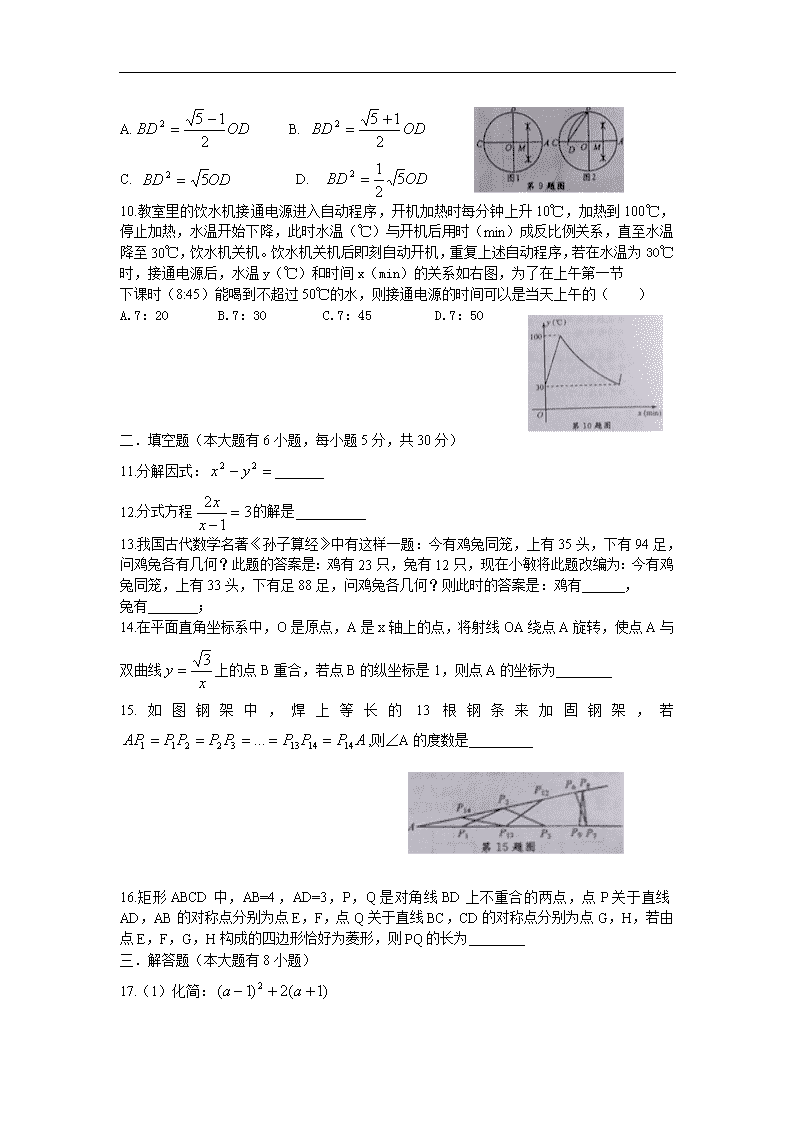
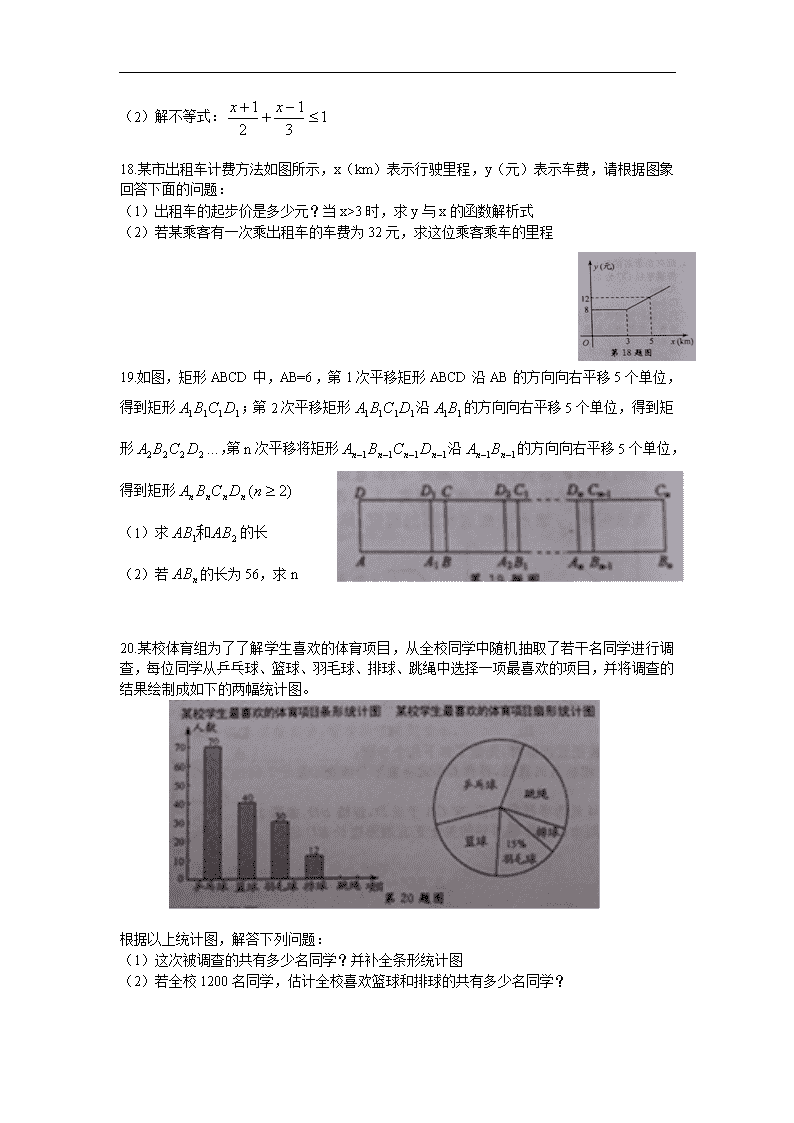
绍兴市2013年中考数学卷 一． 选择题（本大题有10小题，每小题4分，共40分）‎ ‎1.-2的绝对值是（ ）‎ A.2 B.‎-2 ‎‎ C.0 D.‎ ‎2.计算‎3a.2b的结果是（ ）‎ A.3ab B‎.6a C.6ab D.5ab ‎3.地球半径约为‎6400000米，则此数用科学记数法表示为（ ）‎ A. B. C. D. ‎ ‎4.由5个相同的立方体搭成的几何体如图所示，则它的主视图是（ ）‎ ‎5.一个不透明的袋子中有3个白球，2个黄球和1个红球，这些球除颜色可以不同外其他完全相同，则从袋子中随机摸出一个球是黄球的概率为（ ）‎ A. B. C. D. ‎ ‎6.绍兴是著名的桥乡，如图，圆拱桥的桥顶到水面的距离CD为‎8m，桥拱半径OC为‎5m，则水面宽AB为（ ）‎ A‎.4m B‎.5m C‎.6m D‎.8m ‎7.若圆锥的轴截面为等边三角形，则称此圆锥为正圆锥，则正圆锥侧面展开图的圆心角是（ ）‎ A.90° B.120° C.150° D.180°‎ ‎8.如图是我国古代计时器“漏壶”的示意图，在壶内盛一定量的水，水从壶底的小孔漏出，壶壁内画有刻度，人们根据壶中水面的位置计时，用x表示时间，y表示壶底到水面的高度，则y与x的函数关系的图象是（ ）‎ ‎9.小敏在作⊙O的内接正五边形时，先做了如下几个步骤：‎ ‎（1）作⊙O的两条互相垂直的直径，再作OA的垂直平分线交OA于点M，‎ 如图1.‎ ‎（2）以M为圆心，BM长为半径作圆弧，交CA于点D，连接BD，如图2.‎ 若⊙O的半径为1，则由以上作图得到的关于正五边形边长BD的等式是（ ）‎ A. B. ‎ C. D. ‎ ‎10.教室里的饮水机接通电源进入自动程序，开机加热时每分钟上升‎10℃‎，加热到‎100℃‎，停止加热，水温开始下降，此时水温（℃）与开机后用时（min）成反比例关系，直至水温降至‎30℃‎，饮水机关机。饮水机关机后即刻自动开机，重复上述自动程序，若在水温为‎30℃‎时，接通电源后，水温y（℃）和时间x（min）的关系如右图，为了在上午第一节 下课时（8:45）能喝到不超过‎50℃‎的水，则接通电源的时间可以是当天上午的（ ）‎ A.7：20 B.7：‎30 ‎‎ C.7：45 D.7：50‎ 一． 填空题（本大题有6小题，每小题5分，共30分）‎ ‎11.分解因式： ‎ ‎12.分式方程的解是 ‎ ‎13.我国古代数学名著《孙子算经》中有这样一题：今有鸡兔同笼，上有35头，下有94足，问鸡兔各有几何？此题的答案是：鸡有23只，兔有12只，现在小敏将此题改编为：今有鸡兔同笼，上有33头，下有足88足，问鸡兔各几何？则此时的答案是：鸡有 ，‎ 兔有 ；‎ ‎14.在平面直角坐标系中，O是原点，A是x轴上的点，将射线OA绕点A旋转，使点A与双曲线上的点B重合，若点B的纵坐标是1，则点A的坐标为 ‎ ‎15.如图钢架中，焊上等长的13根钢条来加固钢架，若,则∠A的度数是 ‎ ‎16.矩形ABCD中，AB=4，AD=3，P，Q是对角线BD上不重合的两点，点P关于直线AD，AB的对称点分别为点E，F，点Q关于直线BC，CD的对称点分别为点G，H，若由点E，F，G，H构成的四边形恰好为菱形，则PQ的长为 ‎ 三．解答题（本大题有8小题）‎ ‎17.（1）化简：‎ ‎（2）解不等式：‎ ‎18.某市出租车计费方法如图所示，x（km）表示行驶里程，y（元）表示车费，请根据图象回答下面的问题：‎ ‎（1）出租车的起步价是多少元？当x>3时，求y与x的函数解析式 ‎（2）若某乘客有一次乘出租车的车费为32元，求这位乘客乘车的里程 ‎19.如图，矩形ABCD中，AB=6，第1次平移矩形ABCD沿AB的方向向右平移5个单位，得到矩形；第2次平移矩形沿的方向向右平移5个单位，得到矩形…，第n次平移将矩形沿的方向向右平移5个单位，得到矩形 ‎（1）求的长 ‎（2）若的长为56，求n ‎20.某校体育组为了了解学生喜欢的体育项目，从全校同学中随机抽取了若干名同学进行调查，每位同学从乒乓球、篮球、羽毛球、排球、跳绳中选择一项最喜欢的项目，并将调查的结果绘制成如下的两幅统计图。‎ 根据以上统计图，解答下列问题：‎ ‎（1）这次被调查的共有多少名同学？并补全条形统计图 ‎（2）若全校1200名同学，估计全校喜欢篮球和排球的共有多少名同学？‎ ‎21.如图，伞不论张开还是收紧，伞柄AP始终平分同一平面内两条伞架所成的角∠BAC，当伞收紧时，动点D与点M重合，且点A，E，D在同一条直线上，已知部分伞架的长度如下：‎ ‎（1）求AM的长 ‎（2）当∠BAC=104°时，求AD的长（精确到‎1cm）‎ ‎22.若一个矩形的一边是另一边的两倍，则称这个矩形为方形，如图1，矩形ABCD中，BC=2AB，则称ABCD为方形，‎ ‎（1）设a，b是方形的一组邻边长，写出a，b的值（一组即可）‎ ‎（2）在⊿ABC中，将AB，AC分别五等分，连接两边对应的等分点，以这些连接线为一边作矩形，使这些矩形的边,,，的对边分别在，，，BC上，如图2所示，‎ ‎①若BC=25，BC边上的高为20，判断以为一边的矩形是不是方形？为什么 ‎②若以为一边的矩形是方形，求BC与BC边上的高之比 ‎23.在⊿ABC中，∠CAB=90°，AD⊥BC于点D，点E为AB的中点，EC与AD交于点G点F在BC上，‎ ‎（1）如图1，AC：AB=1:2,EF⊥CB，求证：EF=CD ‎（2）如图2，AC：AB=，EF⊥CE，求EF：EG的值 ‎24.抛物线与x轴交于A，B两点（点A在点B左侧）与y轴交于点C，点D为顶点，‎ ‎（1）求点B及点D的坐标 ‎（2）连接BD，CD，抛物线的对称轴与x轴交于点E ‎①若线段BD上一点P，使∠DCP=∠BDE，求点P的坐标 ‎②若抛物线上一点M，作MN⊥CD，交直线CD于点N，使∠CMN=∠BDE，求点M的坐标