中考数学真题分类汇编滚动小专题十一与圆的有关计算与证明答案不全

中考数学真题分类汇编滚动小专题十一与圆的有关计算与证明答案不全

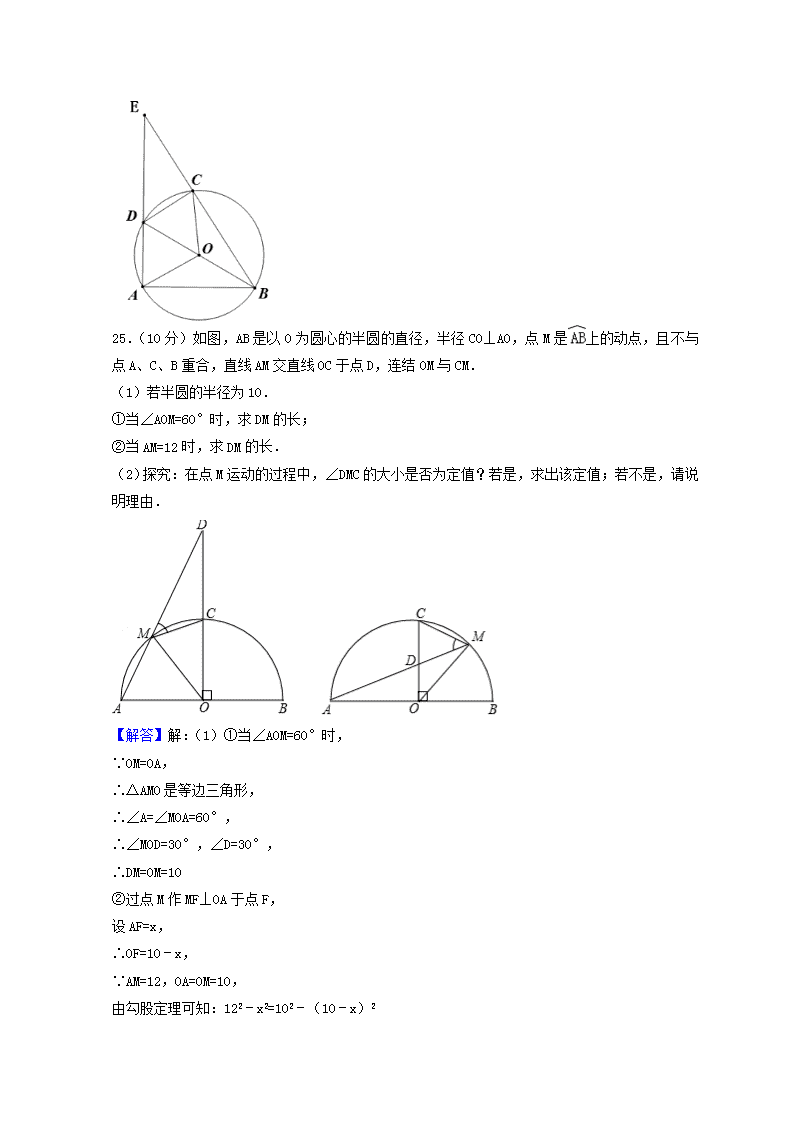
（分类）滚动小专题（十一）与圆有关的计算与证明 类型 1 与圆的基本性质有关的计算与证明 （2018·安徽）20.如图,⊙O 为锐角△ABC 的外接圆,半径为 5. （1）用尺规作图作出∠BAC 的平分线，并标出它与劣弧 BC 的交点 E(保留作图痕迹,不写作法)； （2）若（1）中的点 E 到弦 BC 的距离为 3,求弦 CE 的长. 解：（1）画图略 （2）∵AE 平分∠BAC ∴弧 BE=弧 EC，连接 OE 则 OE⊥BC 于点 F，EF=3 连接 OC、EC 在 Rt△OFC 中，由勾股定理可得 FC= 21 在 Rt△EFC 中，由勾股定理可得 CE= 30 （2018 湖州） 21．（8 分）（2018•湖州）如图，已知 AB 是⊙O 的直径，C，D 是⊙O 上的点，OC∥BD，交 AD 于点 E，连结 BC． （1）求证：AE=ED； （2）若 AB=10，∠CBD=36°，求 的长． （2018 无锡）24、（本题满分 8 分）如图，四边形 ABCD 内接于圆心 O，AB=17，CD=10，∠A=90°， cos B= 5 3 ，求 AD 的长。 【解答】 DA⊥AB ∠DAB=90° 在圆 O 中 ∠DCB=90° 延长 AD、BC 交于点 E，易证∠B=∠EDC  5 3 ED DC  3 50ED  5 3cos B  3 4tan B 在△EAB 中，EA= 3 68 3 417  DA=EA-ED= 3 50 3 68  =6 25．（10 分）如图，AB 是以 O 为圆心的半圆的直径，半径 CO⊥AO，点 M 是 上的动点，且不与 点 A、C、B 重合，直线 AM 交直线 OC 于点 D，连结 OM 与 CM． （1）若半圆的半径为 10． ①当∠AOM=60°时，求 DM 的长； ②当 AM=12 时，求 DM 的长． （2）探究：在点 M 运动的过程中，∠DMC 的大小是否为定值？若是，求出该定值；若不是，请说 明理由． 【解答】解：（1）①当∠AOM=60°时， ∵OM=OA， ∴△AMO 是等边三角形， ∴∠A=∠MOA=60°， ∴∠MOD=30°，∠D=30°， ∴DM=OM=10 ②过点 M 作 MF⊥OA 于点 F， 设 AF=x， ∴OF=10﹣x， ∵AM=12，OA=OM=10， 由勾股定理可知：122﹣x2=102﹣（10﹣x）2 ∴x= ， ∴AF= ， ∵MF∥OD， ∴△AMF∽△ADO， ∴ ， ∴ ， ∴AD= ∴MD=AD﹣AM= （2）当点 M 位于 之间时， 连接 BC， ∵C 是 的重点， ∴∠B=45°， ∵四边形 AMCB 是圆内接四边形， 此时∠CMD=∠B=45°， 当点 M 位于 之间时， 连接 BC， 由圆周角定理可知：∠CMD=∠B=45° 综上所述，∠CMD=45° （2018 温州）22.（本题 10 分）如图，D 是△ABC 的 BC 边上一点，连接 AD，作△ABD 的外接圆， 将△ADC 沿直线 AD 折叠，点 C 的对应点 E 落在上. （1）求证：AE=AB. （2）若∠CAB=90°，cos∠ADB= 1 3 ，BE=2，求 BC 的长. （2018 台州）24.如图， ABC 是 O 的内接三角形，点 D 在 BC 上，点 E 在弦 AB 上（ E 不 与 A 重合），且四边形 BDCE 为菱形. （1）求证： AC CE ； （2）求证： 2 2BC AC AB AC   ； （3）已知 O 的半径为 3. ①若 5 3 AB AC  ，求 BC 的长； ②当 AB AC 为何值时， AB AC 的值最大？ （2018 南通）28.如图， O 的直径 26AB  ，P 是 AB 上（不与点 A B、 重合）的任一点，点 C D、 为 O 上的两点.若 APD BPC   ，则称 CPD 为直径 AB 的“回旋角”. （1）若 60BPC DPC     ，则 CPD 是直径 AB 的 “回旋角”吗？并说明理由； （2）若 CD 的长为 13 4  ，求“回旋角” CPD 的度数； （3）若直径 AB 的“回旋角”为120 ，且 PCD 的周长为 24 13 3 ，直接写出 AP 的长. 解：28．（1）是； （2）45°； （3）3 或 23． （2018 湘潭） （2018 南京）26.如图，在正方形 ABCD 中，E 是 AB 上一点，连接 DE .过点 A 作 AF DE ， 垂足为 F . O 经过点C 、 D 、 F ，与 AD 相交于点G . （1）求证 AFG DFC∽△ △ ； （ 2 ） 若 正 方 形 ABCD 的 边 长 为 4 ， 1AE  ， 求 O 的 半 径 （2018 黄冈）18. 如图， AD 是 O 的直径， AB 为 O 的弦，OP AD ，OP 与 AB 的延长 线交于点 P ，过 B 点的切线交OP 于点 C . （1）求证： CBP ADB   . （2）若 2OA  ， 1AB  ，求线段 BP 的长. （2018 宜昌）21. 如图，在 ABC 中，AB AC . 以 AB 为直径的半圆交 AC 于点 D ，交 BC 于点 E .延长 AE 至点 F，使 EF AE ,连接 FB FC， . (1)求证:四边形 ABFC 是菱形； (2) 若 AD 7 BE 2 ， ，求半圆和菱形 ABFC 的面积. 21.(1)证明： AB 为半圆的直径， 90AEB   , AB AC , CE BE  , 又 EF AE , ∴四边形 ABFC 是平行四边形. 又 AB AC ,（或 90AEB   ，） ∴平行四边形 ABFC 是菱形. (2)解：∵ 7, 2AD BE CE   , 设CD x ，则 7AB AC x   ， 解法一：连接 BD ，（如图） 图 1 ∵ AB 为半圆的直径， 90ADB   , 2 2 2 2AB AD CB CD    2 2 2 2(7 ) 7 4x x     1 1x  或 2 8x   （舍去） 解法二：连接 DE .（如图） 图 2 ∵四边形 ABED 是圆内接四边形 180ADE ABC     180ADE CDE     CDE ABE   DCE BCA   CDE CBA ∽ CD CB CE CA   4 2 7 x x    2 7 8 0x x    1 1x  或 2 8x   （舍去） 解法三：如图 1，连接 BD ， AB 为半径的直径， 90ADB   可证 CDB CEA ∽ CD CB CE CA   4 2 7 x x    1 1x  或 2 8x   （舍去） 21= 4 =82S    半圆 15BD  , =8 15S 菱形 （2018 福建） （2018 张家界）20、（本小题满分 6 分） 如图，点 P 是⊙O 的直径 AB 延长线上一点,且 AB =4,点 M 为 上一个动点(不与 BA、 重合),射线 PM 与⊙O 交于点 N (不与 M 重合) (1) 当 M 在什么位置时, MAB 的面积最大,并求岀这个最大值； (2)求证: PAN ∽ PMB . 20.解：（1）当点 M 在 AB 弧的中点处时， 最大 ………………1 分 （其它表述合理均给分） 因为此时： 242 1 2 1  ABOM ………………2 分 4242 1 2 1   OMABS ABM ……………3 分 （2） PANPMB  …………4 分 PP  …………5 分 PMB∽  PAM …………6 分 （2018 贵阳） 23.（本题满分 10 分）如图，AB 为⊙ O 的直径，,，且，AB 4 ，点 C 在半圆上，OC AB ， 垂足为点O ，P 为半圆上任意一点，过 P 点作 PE OC 于点 E，设 OPE 的内心 为 M ,连接OM、PM . （1）求 OMP 的度数； （2）当点 P 在半圆上从点 B 运动到点 A 时，求内心 M 所经过的路径长. ABMS 【解】（1）∵ PE OC ∴ PEO 90 ∴ EPO EOP 90 ∵ M 是 OPE 的内心 ∴ EOM POM， EPM OPM ∴ POM OPM 1 ( EPO EOP) 45 2 在 POM 中， OMP 180 ( POM OPM ) 180 45 135 （2）连接CM ，作过O、M、C 三点的外接圆，即⊙ N ，连接 NC、NO ，在⊙ N 的优弧上任取一点 H ，连接 HC、HO .如图所示： 由题意知：OP OC， POM COM，OM OM ∴ POM ≌ COM ∴ OMP OMC 135 在⊙ N 的内接四边形CMOH 中， H 180 OMC 180 135 45 ∴ N 2 45 90 由题意知：OC 1 AB 1 4 2 2 2 在等腰直角三角形CNO 中， NC NO 由勾股定理得： NC 2 NO 2 OC 2 即 2 NC 2 22 NC 2 当点 P 在 上运动时，点 M 在 上运动 90∴ 的长为： 180 ∵ 与 关于 OC 对称 2 2 2 ∴当点 P 在 上运动时，点 M 所在弧上的运动路径长与当点 P 在 上运动时，点 M 在 上运动的路径长相等 ∴当点 P 在半圆上从点 B 运动到点 A 时，求内心 M 所经过的路径长为： 2 2 2 2 （2018 遵义） 25. (12 分)如图，AB 是半圆O 的直径，C是AB 延长线上的点，AC 的垂直平分线交半圆于点 D，交 AC 于点 E，连接 DA，DC.已知半圆 0 的半径为 3，BC=2. (1) 求AD 的长. (2) 点P 是线段AC 上一动点，连接 DP，作∠DPF=∠DAC，PF 交线段CD 于点F.当∆DPF 为等腰三角形时，求 AP 的长. （2018 哈尔滨） 类型 2 与切线有关的计算与证明 （2018 十堰）23.如图， ABC 中， AB AC ，以 AB 为直径的 O 交 BC 于点 D ，交 AC 于点 E ，过点 D 作 FG AC 于点 F ，交 AB 的延长线于点G . （1）求证： FG 是 O 的切线； （2）若 tan 2C  ，求 GB GA 的值. （2018·德州）22.如图, AB 是 O 的直径,直线CD 与 O 相切于点C ,且与 AB 的延长线交于点 E .点C 是 BF 的 中点. (1)求证: AD CD (2)若 30CAD   . O 的半径为 3，一只蚂蚁从点 B 出发，沿着 BE CEC B  爬回至点 B ,求蚂蚁爬过的路程  3.14 3 1.73  ， 结果保留一位小数. （2018·绵阳）如图，AB 是 O 的直径，点 D 在 O 上（点 D 不与 A，B 重合），直线 AD 交过点 B 的切线于点 C， 过点 D 作 O 的切线 DE 交 BC 于点 E。 （1）求证：BE=CE； （2）若 DE 平行 AB，求 ACOsin 的值。 （2018·滨州）22.如图，AB 为 O 的直径,点C 在 O 上, AD CD 于点 D ,且 AC 平分 DAB .求证;(1)直线 DC 是 O 的切线;(2) 2 2AC AD AO  . （2018 内江）26.如图，以 Rt ABC 的直角边 AB 为直径作 O 交斜边 AC 于点 D ，过圆心O 作 / /OE AC ，交 BC 于点 E ，连接 DE . （1）判断 DE 与 O 的位置关系并说明理由； （2）求证： 22DE CD OE  ； （3）若 4tan 3C  ， 5 2DE  ，求 AD 的长. （2018•内江）如图，以 Rt△ABC 的直角边 AB 为直径作⊙O 交斜边 AC 于点 D，过圆心 O 作 OE∥AC，交 BC 于点 E， 连接 DE． （1）判断 DE 与⊙O 的位置关系并说明理由； （2）求证：2DE2=CD•OE； （3）若 tanC= ，DE= ，求 AD 的长． 【解答】解：（1）DE 是⊙O 的切线，理由：如图， 连接 OD，BD，∵AB 是⊙O 的直径， ∴∠ADB=∠BDC=90°， ∵OE∥AC，OA=OB， ∴BE=CE， ∴DE=BE=CE， ∴∠DBE=∠BDE， ∵OB=OD， ∴∠OBD=∠ODB， ∴∠ODE=∠OBE=90°， ∵点 D 在⊙O 上， ∴DE 是⊙O 的切线； （2）∵∠BCD=∠ABC=90°，∠C=∠C， ∴△BCD∽△ACB， ∴ ， ∴BC2=CD•AC， 由（1）知 DE=BE=CE= BC， ∴4DE2=CD•AC， 由（1）知，OE 是△ABC 是中位线， ∴AC=2OE， ∴4DE2=CD•2OE， ∴2DE2=CD•OE； （3）∵DE= ， ∴BC=5， 在 Rt△BCD 中，tanC= = ， 设 CD=3x，BD=4x，根据勾股定理得，（3x）2+（4x）2=25， ∴x=﹣1（舍）或 x=1， ∴BD=4，CD=3， 由（2）知，BC2=CD•AC， ∴AC= = ， ∴AD=AC﹣CD= ﹣3= ． （2018·甘肃） （2018·南充）22.如图，C 是 O 上一点，点 P 在直径 AB 的延长线上， O 的半径为 3， 2PB  ， 4PC  . （1）求证： PC 是 O 的切线. （2）求 tan CAB 的值. 22.解：（1）证明：连接 OC . ∵ O 的半径为 3，∴ 3OC OB  . 又∵ 2BP  ，∴ 5OP  . 在 OCP 中， 2 2 2 2 2 23 4 5OC PC OP     ， ∴ OCP 为直角三角形， 90OCP   . ∴OC PC ，故 PC 为 O 的切线. （2）过C 作CD OP 于点 D ， 90ODC OCP     . ∵ COD POC   ，∴ OCD OPC   . ∴ OC OP PC OD OC CD   ，∴ 2OC OD OP  ，∴ 2 9 5 OCOD OP   ， 4 5 3DC  ，∴ 12 5CD  . 又∵ 24 5AD OA OD   ， ∴在 Rt CAD 中， 1tan 2 CDCAB AD    . （2018·金华/丽水）如图，在 Rt△ABC 中，点 O 在斜边 AB 上，以 O 为圆心，OB 为半径作圆，分别与 BC,AB 相交于 点 D,E，连结 AD.已知∠CAD=∠B. （1）求证：AD 是⊙O 的切线. （2）若 BC=8，tanB= 1 2 ,求⊙O 的半径. （2018 宁波） （2018 衢州）如图，已知 AB 为⊙O 直径，AC 是⊙O 的切线，连接 BC 交⊙O 于点 F，取弧 BF 的中点 D，连接 AD 交 BC 于点 E，过点 E 作 EF⊥AB 于 H。 （1）求证：△HBE∽△ABC； （2）若 CF＝4，BF＝5，求 AC 和 EH 的长。 （2018·枣庄）23．如图，在 Rt ACB 中， 090C ， cmBCcmAC 4,3  ，以 BC 为直径作⊙O 交 AB 于 点 D . （1）求线段 AD 的长度； （2）点 F 是线段 AC 上的一点，试问：当点 E 在什么位置时，直线 ED 与⊙O 相切？请说明理由. 解：（1）在 Rt△ACB 中，∵AC=3cm，BC=4cm，∠ACB=90°，∴AB=5cm； 连接 CD，∵BC 为直径， ∴∠ADC=∠BDC=90°； ∵∠A=∠A，∠ADC=∠ACB， ∴Rt△ADC∽Rt△ACB； ∴ ，∴ ； （2）当点 E 是 AC 的中点时，ED 与⊙O 相切； 证明：连接 OD， ∵DE 是 Rt△ADC 的中线； ∴ED=EC， ∴∠EDC=∠ECD； ∵OC=OD， ∴∠ODC=∠OCD； ∴∠EDO=∠EDC+∠ODC=∠ECD+∠OCD=∠ACB=90°； ∴ED⊥OD， ∴ED 与⊙O 相切． （2018 成都）20.如图，在 Rt ABC 中， 90C   ，AD 平分 BAC 交 BC 于点 D ，O 为 AB 上一点，经过点 A ， D 的 O⊙ 分别交 AB ， AC 于点 E ， F ，连接OF 交 AD 于点G . （1）求证： BC 是 O⊙ 的切线； （2）设 AB x ， AF y ，试用含 ,x y 的代数式表示线段 AD 的长； （3）若 8BE  ， 5sin 13B  ，求 DG 的长. 23．（10 分）（2018•自贡）如图，在△ABC 中，∠ACB=90°． （1）作出经过点 B，圆心 O 在斜边 AB 上且与边 AC 相切于点 E 的⊙O（要求：用尺规作图，保留作图痕迹，不写作 法和证明） （2）设（1）中所作的⊙O 与边 AB 交于异于点 B 的另外一点 D，若⊙O 的直径为 5，BC=4；求 DE 的长．（如果用尺 规作图画不出图形，可画出草图完成（2）问） 解：（1）⊙O 如图所示； （2）作 OH⊥BC 于 H． ∵AC 是⊙O 的切线， ∴OE⊥AC， ∴∠C=∠CEO=∠OHC=90°， ∴四边形 ECHO 是矩形， ∴OE=CH= ，BH=BC﹣CH= ， 在 Rt△OBH 中，OH= =2， ∴EC=OH=2，BE= =2 ， ∵∠EBC=∠EBD，∠BED=∠C=90°， ∴△BCE∽△BED， ∴ = ， ∴ = ， ∴DE= ． （2018 泸州）24.如图 10，已知 AB，CD 是⊙O 的直径，过点 C 作⊙O 的切线交 AB 的延长线于点 P，⊙O 的弦 DE 交 AB 于点 F，且 DF=EF. （1）求证： 2CO OF OP  ； （2）连接 EB 交 CD 于点 G，过点 G 作 GH  AB 于点 H，若 PC= 4 2 ，PB=4，求 GH 的长. 【解答】（1）证明：∵PC 是⊙O 的切线， ∴OC⊥PC， ∴∠PCO=90°， ∵AB 是直径，EF=FD， ∴AB⊥ED， ∴∠OFD=∠OCP=90°， ∵∠FOD=∠COP， ∴△OFD∽△OCP， ∴ = ，∵OD=OC， ∴OC2=OF•OP． （2）解：如图作 CM⊥OP 于 M，连接 EC、EO．设 OC=OB=r． 在 Rt△POC 中，∵PC2+OC2=PO2， ∴（4 ）2+r2=（r+4）2， ∴r=2， ∵CM= = ， ∵DC 是直径， ∴∠CEF=∠EFM=∠CMF=90°， ∴四边形 EFMC 是矩形， ∴EF=CM= ， 在 Rt△OEF 中，OF= = ， ∴EC=2OF= ， ∵EC∥OB， ∴ = = ， ∵GH∥CM， ∴ = = ， ∴GH= ． （2018 宜宾）23．（10 分）（2018•宜宾）如图，AB 为圆 O 的直径，C 为圆 O 上一点，D 为 BC 延长线一点，且 BC=CD， CE⊥AD 于点 E． （1）求证：直线 EC 为圆 O 的切线； （2）设 BE 与圆 O 交于点 F，AF 的延长线与 CE 交于点 P，已知∠PCF=∠CBF，PC=5，PF=4，求 sin∠PEF 的值． 【解答】解：（1）证明：∵CE⊥AD 于点 E ∴∠DEC=90°， ∵BC=CD， ∴C 是 BD 的中点，又∵O 是 AB 的中点， ∴OC 是△BDA 的中位线， ∴OC∥AD ∴∠OCE=∠CED=90° ∴OC⊥CE，又∵点 C 在圆上， ∴CE 是圆 O 的切线． （2）连接 AC ∵AB 是直径，点 F 在圆上 ∴∠AFB=∠PFE=90°=∠CEA ∵∠EPF=∠EPA ∴△PEF∽△PEA ∴PE2=PF×PA ∵∠FBC=∠PCF=∠CAF 又∵∠CPF=∠CPA ∴△PCF∽△PAC ∴PC2=PF×PA ∴PE=PC 在直角△PEF 中，sin∠PEF= = ． （2018 衡阳）23.如图， O 是 ABC 的外接圆，AB 为直径， BAC 的平分线交 O 于点 D ，过点 D 作 DE AC 分别交 AC 、 AB 的延长线于点 E 、 F . （1）求证： EF 是 O 的切线； （2）若 4AC  ， 2CE  ，求 BD 的长度.（结果保留 ） 解：（1）如图，连接 OD， ∵OA=OD， ∴∠OAD=∠ODA， ∵AD 平分∠EAF， ∴∠DAE=∠DAO， ∴∠DAE=∠ADO， ∴OD∥AE， ∵AE⊥EF， ∴OD⊥EF， ∴EF 是⊙O 的切线； （2）如图，作 OG⊥AE 于点 G，连接 BD， 则 AG=CG= AC=2，∠OGE=∠E=∠ODE=90°， ∴四边形 ODEG 是矩形， ∴OA=OB=OD=CG+CE=2+2=4，∠DOG=90°， ∵∠DAE=∠BAD，∠AED=∠ADB=90°， ∴△ADE∽△ABD， ∴ = ，即 = ， ∴AD2=48， 在 Rt△ABD 中，BD= =4， 在 Rt△ABD 中，∵AB=2BD， ∴∠BAD=30°， ∴∠BOD=60°， 则 的长度为 = ． （2018 聊城） 24.如图，在 Rt ABC 中， 90C   ，BE 平分 ABC 交 AC 于点 E ，作 ED EB 交 AB 于点 D ， O 是 BED 的外接圆. （1）求证： AC 是 O 的切线； （2）已知 O 的半径为 2.5， 4BE  ，求 BC ， AD 的长. （2018 泰州）22.如图， AB 为 O☉ 的直径， C 为 O☉ 上一点， ABC∠ 的平分线交 O☉ 于点 D ， DE BC 于点 E . (1)试判断 DE 与 O☉ 的位置关系，并说明理由. (2)过点 D 作 DF AB 于点 F ，若 3 3BE  ， 3DF  ，求图中阴影部分的面积. 解：（1）DE 与⊙O 相切， 理由：连接 DO， ∵DO=BO， ∴∠ODB=∠OBD， ∵∠ABC 的平分线交⊙O 于点 D， ∴∠EBD=∠DBO， ∴∠EBD=∠BDO， ∴DO∥BE， ∵DE⊥BC， ∴∠DEB=∠EDO=90°， ∴DE 与⊙O 相切； （2）∵∠ABC 的平分线交⊙O 于点 D，DE⊥BE，DF⊥AB， ∴DE=DF=3， ∵BE=3 ， ∴BD= =6， ∵sin∠DBF= = ， ∴∠DBA=30°， ∴∠DOF=60°， ∴sin60°= = = ， ∴DO=2 ， 则 FO= ， 故图中阴影部分的面积为： ﹣ × ×3=2π﹣ ． （2018 白银、武威、张掖）20.如图，在 ABC 中， 90ABC   . （1）作 ACB 的平分线交 AB 边于点O ，再以点O 为圆心，OB 的长为半径作 O ；（要求：不写作法，保留作 图痕迹） （2）判断（1）中 AC 与 O 的位置关系，直接写出结果. 20.解：（1）如图,作出角平分线 CO; 作出⊙O. （2）AC 与⊙O 相切． （2018 白银、武威、张掖）27.如图，点O 是 ABC 的边 AB 上一点， O 与边 AC 相切于点 E ，与边 BC ， AB 分别相交于点 D ， F ，且 DE EF . （1）求证： 90C   ； （2）当 3BC  ， 3sin 5A  时，求 AF 的长. 27．（1）证明：连接 OE,BE． ∵ DE=EF，∴ DE︵=EF︵,∴ ∠OBE=∠DBE. ∵ OE=OB,∴∠OEB=∠OBE, ∴∠OEB =∠DBE,∴OE∥BC. ∵⊙O 与边 AC 相切于点 E，∴ OE⊥AC． ∴BC⊥AC,∴∠C=90°. （2）解：在△ABC 中，∠C=90°，BC=3， 3sin 5A  ， ∴AB=5． 设⊙O 的半径为 r，则 AO=5-r， 在 Rt △AOE 中， 3sin 5 5 OE rA OA r    , ∴ 15 8r  ． ∴ 15 55 2 8 4AF     ． （2018 常德）24.如图 12，已知 O 是等边三角形 ABC 的外接圆，点 D 在圆上，在CD 的延长线上有一点 F ,使 DF DA , / /AE BC 交CF 于 E . （1）求证： EA 是 O 的切线； （2）求证： BD CF . 【解答】证明：（1）连接 OD， ∵⊙O 是等边三角形 ABC 的外接圆， ∴∠OAC=30°，∠BCA=60°， ∵AE∥BC， ∴∠EAC=∠BCA=60°， ∴∠OAE=∠OAC+∠EAC=30°+60°=90°， ∴AE 是⊙O 的切线； （2）∵△ABC 是等边三角形， ∴AB=AC，∠BAC=∠ABC=60°， ∵A、B、C、D 四点共圆， ∴∠ADF=∠ABC=60°， ∵AD=DF， ∴△ADF 是等边三角形， ∴AD=AF，∠DAF=60°， ∴∠BAC+∠CAD=∠DAF+∠CAD， 即∠BAF=∠CAF， 在△BAD 和△CAF 中， ∵ ， ∴△BAD≌△CAF， ∴BD=CF． （2018 娄底）25.如图， C D、 是以 AB 为直径的 Oe 上的点， » »AC BC= ，弦 CD 交 AB 于点 E . (1)当 PB是 Oe 的切线时，求证: PBD DABÐ = Ð ； (2)求证: 2 2BC CE CE DE- = × ； (3)已知 OA=4 ， E 是半径 OA 的中点，求线段 DE 的长. 解：（1）∵AB 是⊙O 的直径， ∴∠ADB=90°，即∠BAD+∠ABD=90°， ∵PB 是⊙O 的切线， ∴∠ABP=90°，即∠PBD+∠ABD=90°， ∴∠BAD=∠PBD； （2）∵∠A=∠C、∠AED=∠CEB， ∴△ADE∽△CBE， ∴ = ，即 DE•CE=AE•BE， 如图，连接 OC， 设圆的半径为 r，则 OA=OB=OC=r， 则 DE•CE=AE•BE=（OA﹣OE）（OB+OE）=r2﹣OE2， ∵ = ， ∴∠AOC=∠BOC=90°， ∴CE2=OE2+OC2=OE2+r2，BC2=BO2+CO2=2r2， 则 BC2﹣CE2=2r2﹣（OE2+r2）=r2﹣OE2， ∴BC2﹣CE2=DE•CE； （3）∵OA=4， ∴OB=OC=OA=4， ∴BC= =4 ， 又∵E 是半径 OA 的中点， ∴AE=OE=2， 则 CE= = =2 ， ∵BC2﹣CE2=DE•CE， ∴（4 ）2﹣（2 ）2=DE•2 ， 解得：DE= ． （2018 永州）24.如图，线段 AB 为 O 的直径，点C 、 E 在 O 上，  BC CE ，CD AB ，垂足为点 D ，连 接 BE ，弦 BE 与线段CD 相交于点 F . （1）求证：CF BF ； （2）若 4cos 5ABE  ，在 AB 的延长线上取一点 M ，使 4BM  ， O 的半径为 6 ，求证：直线CM 是 O 的 切线. 25、(本题满分 10 分)如图，已知 AB 为⊙O 的直径，AB=8，点 C 和点 D 是⊙O 上关于直线 AB 对称的两个点，连接 OC、AC，且∠BOC＜90°，直线 BC 和直线AD 相交于点 E，过点 C 作直线 CG 与线段 AB 的延长线相交于点 F，与直线 AD 相交于点 G，且∠GAF＝∠GCE （1）求证：直线 CG 为⊙O 的切线； （2）若点 H 为线段 OB 上一点，连接 CH，满足 CB＝CH， ①△CBH∽△OBC； ②求 OH＋HC 的最大值. （1）证明：∵C、D 关于 AB 对称 ∴∠GAF=∠CAF ∵∠GAF=∠GCE,∴∠GCE=∠CAF ∵OA=OC,∴∠CAF=∠ACO,∴∠GCE=∠ACO ∵AB 为直径 ∴∠ACO+∠OCB=90° ∴∠GCE+∠OCB=90° 即∠OCG=90°，∴CG 为圆 O 的切线. （2）①∵OC=OB,CH=BC ∴∠OCB=∠OBC,∠CHB=∠CBH ∠CBH=∠OBC=∠OCB=∠CHB △CBH∽△OBC ② 4, 2BCBMOB BC BC BH  设 BC=x，则 CH=x，BH= 4 2x   524 144 1 22  xxxHCOH ∴当 x=2 时，最大值为 5. （2018 宿迁）26. （本题满分 10 分） 如图，AB、AC 分别是 O 的直径和弦，OD⊥AC 于点 D，过点 A 作 O 的切线与 OD 的延长线交于点 P，PC、AB 的延长 线交于点 F. ⑴ 求证：PC 是 O 的切线； ⑵ 若∠ABC=600,AB=10,求线段 CF 的长， （2018 盐城）25.如图，在以线段 AB 为直径的 O 上取一点，连接 AC 、BC .将 ABC 沿 AB 翻折后得到 ABD . （1）试说明点 D 在 O 上； （2）在线段 AD 的延长线上取一点 E ，使 2AB AC AE  .求证： BE 为 O 的切线； （3）在（2）的条件下，分别延长线段 AE 、CB 相交于点 F ，若 2BC  ， 4AC  ，求线段 EF 的长. （2018 扬州）25.如图，在 ABC 中， AB AC ， AO BC 于点O ，OE AB 于点 E ，以点O 为圆心，OE 为 半径作半圆，交 AO 于点 F . （1）求证： AC 是 O 的切线； （2）若点 F 是 AO 的中点， 3OE  ，求图中阴影部分的面积； （3）在（2）的条件下，点 P 是 BC 边上的动点，当 PE PF 取最小值时，直接写出 BP 的长. （1）证明：作 OH⊥AC 于 H，如图， ∵AB=AC，AO⊥BC 于点 O， ∴AO 平分∠BAC， ∵OE⊥AB，OH⊥AC， ∴OH=OE， ∴AC 是⊙O 的切线； （2）解：∵点 F 是 AO 的中点， ∴AO=2OF=3， 而 OE=3， ∴∠OAE=30°，∠AOE=60°， ∴AE= OE=3 ， ∴图中阴影部分的面积=S△AOE﹣S 扇形 EOF= ×3×3 ﹣ = ； （3）解：作 F 点关于 BC 的对称点 F′，连接 EF′交 BC 于 P，如图， ∵PF=PF′， ∴PE+PF=PE+PF′=EF′，此时 EP+FP 最小， ∵OF′=OF=OE， ∴∠F′=∠OEF′， 而∠AOE=∠F′+∠OEF′=60°， ∴∠F′=30°， ∴∠F′=∠EAF′， ∴EF′=EA=3 ， 即 PE+PF 最小值为 3 ， 在 Rt△OPF′中，OP= OF′= ， 在 Rt△ABO 中，OB= OA= ×6=2 ， ∴BP=2 ﹣ = ， 即当 PE+PF 取最小值时，BP 的长为 ． （2018 江西省卷）20.如图，在 ABC 中，O 为 AC 上一点，以点O 为圆心，OC 为半径作圆，与 BC 相切于点C ， 过点 A 作 AD BO 交 BO 的延长线于点 D ，且 AOD BAD   . （1）求证： AB 为 O 的切线； （2）若 6BC  ， 4tan 3ABC  ，求 AD 的长. （2018 呼和浩特） （2018 临沂）（2018•临沂）如图，△ABC 为等腰三角形，O 是底边 BC 的中点，腰 AB 与⊙O 相切于点 D，OB 与⊙O 相交于点 E． （1）求证：AC 是⊙O 的切线； （2）若 BD= ，BE=1．求阴影部分的面积． 【解答】（1）证明：连接 OD，作 OF⊥AC 于 F，如图， ∵△ABC 为等腰三角形，O 是底边 BC 的中点， ∴AO⊥BC，AO 平分∠BAC， ∵AB 与⊙O 相切于点 D， ∴OD⊥AB， 而 OF⊥AC， ∴OF=OD， ∴AC 是⊙O 的切线； （2）解：在 Rt△BOD 中，设⊙O 的半径为 r，则 OD=OE=r， ∴r2+（ ）2=（r+1）2，解得 r=1， ∴OD=1，OB=2， ∴∠B=30°，∠BOD=60°， ∴∠AOD=30°， 在 Rt△AOD 中，AD= OD= ， ∴阴影部分的面积=2S△AOD﹣S 扇形 DOF =2× ×1× ﹣ = ﹣ ． （2018 潍坊） 22．如图, BD 为 ABC 外接圆 O 的直径,且 BAE C   ． (1)求证: AE 与 O 相切于点 A ； (2)若 , 2 7AE BC BC ∥ , 2 2AC  ,求 AD 的长． （2018 天津）21. 已知 AB 是 O 的直径，弦CD 与 AB 相交， 38BAC  . （Ⅰ）如图①，若 D 为 AB 的中点，求 ABC 和 ABD 的大小； （Ⅱ）如图②，过点 D 作 O 的切线，与 AB 的延长线交于点 P ，若 / /DP AC ，求 OCD 的大小. （2018 武汉）21．（本题 8 分）如图，PA 是⊙O 的切线，A 是切点，AC 是直径，AB 是弦，连接 PB、PC，PC 交 AB 于 点 E，且 PA＝PB (1) 求证：PB 是⊙O 的切线 (2) 若∠APC＝3∠BPC，求 CE PE 的值 （2018 邵阳）21．如图（十二）所示，AB 是⊙O 的直径，点 C 为⊙O 上一点，过点 B 作 BD⊥CD， 垂足为点 D，连结 BC．BC 平分∠ABD． 求证：CD 为⊙O 的切线． 21．（8 分） 证 明 ： ∵ B C 平 分 ∠ A B D ， ∴ ∠ O B C ＝ ∠ D B C ． … … … … … … … … … … … … … … … … … 2 分 ∵ O B ＝ O C ， ∴ ∠ O B C ＝ ∠ O C B ． … … … … … … … … … … … … … … … … … … … … 4 分 ∴ ∠ D B C ＝ ∠ O C B ． ∴ O C ∥ B D ． … … … … … … … … … … … … … … … … … … … … 6 分 ∵BD⊥CD，∴OC⊥CD． 又∵点 C 为⊙O 上一点， ∴CD 为⊙O 的切线．…………………………………………………………………8 分 （2018·淄博）22. （本小题满分 8 分） 如图，以 AB 为直径的 O 外接于 ABC ，过 A 点的切线 AP 与 BC 的延长线交于点 P ， APB 的平分线分别交 ,AB AC 于点 ,D E ，其中  ,AE BD AE BD 的长是一元二次方程 2 5 6 0x x   的两个实数根． （1）求证： PA BD PB AE   ； （2）在线段 BC 上是否存在一点 M ，使得四边形 ADME 是菱形？若存在，请给予证明，并求其面积；若不存在， 说明理由. 解：（1）∵DP 平分∠APB， ∴∠APE=∠BPD， ∵AP 与⊙O 相切， ∴∠BAP=∠BAC+∠EAP=90°， ∵AB 是⊙O 的直径， ∴∠ACB=∠BAC+∠B=90°， ∴∠EAP=∠B， ∴△PAE∽△PBD， ∴ ， ∴PA•BD=PB•AE； （2）过点 D 作 DF⊥PB 于点 F，作 DG⊥AC 于点 G， ∵DP 平分∠APB， AD⊥AP，DF⊥PB， ∴AD=DF， ∵∠EAP=∠B， ∴∠APC=∠BAC， 易证：DF∥AC， ∴∠BDF=∠BAC， 由于 AE，BD（AE＜BD）的长是 x2﹣5x+6=0， 解得：AE=2，BD=3， ∴由（1）可知： ， ∴cos∠APC= = ， ∴cos∠BDF=cos∠APC= ， ∴ ， ∴DF=2， ∴DF=AE， ∴四边形 ADFE 是平行四边形， ∵AD=AE， ∴四边形 ADFE 是菱形， 此时点 F 即为 M 点， ∵cos∠BAC=cos∠APC= ， ∴sin∠BAC= ， ∴ ， ∴DG= ， ∴在线段 BC 上是否存在一点 M，使得四边形 ADME 是菱形 其面积为：DG•AE=2× = （2018 德阳） （2018 广东省卷）24.如图，四边形 ABCD 中，AB=AD=CD，以 AB 为直径的⊙O 经过点 C，连接 AC、OD 交于点 E. （1）证明：OD//BC； （2）若 tan∠ABC=2，证明：DA 与⊙O 相切； （3）在（2），连接 BD 交⊙O 于点 F，连接 EF，若 BC=1，求 EF 的长. （2018 菏泽）22.如图， ABC 内接于 O ， AB AC ， 36BAC   ，过点 A 作 / /AD BC ，与 ABC 的平分 线交于点 D ， BD 与 AC 交于点 E ，与 O 交于点 F . （1）求 DAF 的度数； （2）求证： 2AE EF ED  ； （3）求证： AD 是 O 的切线. （2018 随州） （2018 咸宁） （2018 孝感）23.如图， ABC 中， AB AC ，以 AB 为直径的 O 交 BC 于点 D ，交 AC 于点 E ，过点 D 作 DF AC 于点 F ，交 AB 的延长线于点G . （1）求证： DF 是 O 的切线； （2）已知 2 5BD  ， 2CF  ，求 AE 和 BG 的长. （2018 巴中）26. 已知如图 9 所示， ABC 中 30A B     ，CD 是 ABC 的角平分线，以C 为圆心，CD 为 半径画圆，交CA 所在直线于 E 、 F 两点，连接 DE 、 DF . （1）求证：直线 AB 是 C 的切线. （2）若 10AC cm ，求 DF 的长 （2018 郴州）23.已知 BC 是 O 的直径，点 D 是 BC 延长线上一点，AB AD ，AE 是 O 的弦， 30AEC   . （1）求证：直线 AD 是 O 的切线； （2）若 AE BC ，垂足为 M ， O 的半径为 4 ，求 AE 的长. （2018 深圳）22．如图 9，⊙ O 是 ABC 的外接圆， AB AC , 2BC  ， 10cos 10ABC  。点 D 为 AC 上的动点， 连接 AD 并延长，交 BC 的延长线于点 E 。 （1）试求 AB 的长； （2）试判断 AD AE 的值是否为定值？若为定值，请求出这个定值，若不为定值，请说明理由。 （3）如图 10，连接 BD ，过点 A 作 AH ⊥ BD 于点 H ，连接CD ，求证： BH CD DH  。 22.解：(1)作 AM BC , , 2AB AC AM BC BC   1 12BM CM BC   10cos 10 BMB AB   ，在 Rt AMB 中， 1BM  10cos 1 1010AB BM B      . (2)连接 DC AB AC ACB ABC   ∵四边形 ABCD 内接于圆O ， 图 10图 9 180ADC ABC     ， 180ACE ACB     ， ADC ACE   CAE 公共 EAC CAD ∽ AC AE AD AC    22 10 10AD AE AC     . （3）在 BD 上取一点 N ，使得 BN CD 在 ABN 和 ACD 中 3 1 AB AC BN CD        ( )ABN ACD SAS   AN AD  ,AN AD AH BD  NH HD  ,BN CD NH HD  BN NH CD HD BH     . （2018 黔东南、黔西南、黔南）22.如图，CE 是 O 的直径，BC 切 O 于点C ，连接 OB ，作 / /ED OB 交 O 于点 D ， BD 的延长线与CE 的延长线交于点 A . （1）求证： AB 是 O 的切线； （2）若 O 的半径为1， tan 2DEO  ， 1tan 4A  ，求 AE 的长. （2018 恩施）23.如图， AB 为 O 直径， P 点为半径 OA 上异于O 点和 A 点的一个点，过 P 点作与直径 AB 垂直 的弦CD ，连接 AD ，作 BE AB ， / /OE AD 交 BE 于 E 点，连接 AE 、 DE 、 AE 交CD 于 F 点. （1）求证： DE 为 O 切线； （2）若 O 的半径为3 ， 1sin 3ADP  ，求 AD ； （3）请猜想 PF 与 FD 的数量关系，并加以证明. 23．（10 分）（2018•恩施州）如图，AB 为⊙O 直径，P 点为半径 OA 上异于 O 点和 A 点的一个点，过 P 点作与直径 AB 垂直的弦 CD，连接 AD，作 BE⊥AB，OE∥AD 交 BE 于 E 点，连接 AE、DE、AE 交 CD 于 F 点． （1）求证：DE 为⊙O 切线； （2）若⊙O 的半径为 3，sin∠ADP= ，求 AD； （3）请猜想 PF 与 FD 的数量关系，并加以证明． 【解答】证明：（1）如图 1，连接 OD、BD，BD 交 OE 于 M， ∵AB 是⊙O 的直径， ∴∠ADB=90°，AD⊥BD， ∵OE∥AD， ∴OE⊥BD， ∴BM=DM， ∵OB=OD， ∴∠BOM=∠DOM， ∵OE=OE， ∴△BOE≌△DOE（SAS）， ∴∠ODE=∠OBE=90°， ∴DE 为⊙O 切线； （2）设 AP=a， ∵sin∠ADP= = ， ∴AD=3a， ∴PD= = =2 a， ∵OP=3﹣a， ∴OD2=OP2+PD2， ∴32=（3﹣a）2+（2 a）2， 9=9﹣6a+a2+8a2， a1= ，a2=0（舍）， 当 a= 时，AD=3a=2， ∴AD=2； （3）PF=FD， 理由是：∵∠APD=∠ABE=90°，∠PAD=∠BAE， ∴△APF∽△ABE， ∴ ， ∴PF= ， ∵OE∥AD， ∴∠BOE=∠PAD， ∵∠OBE=∠APD=90°， ∴△ADP∽△OEB， ∴ ， ∴PD= ， ∵AB=2OB， ∴PD=2PF， ∴PF=FD． （2018 黄石）21、（本小题 8 分）如图，已知 A、B、C、D、E 是⊙O 上五点，⊙O 的直径 2 3BE  ,∠BCD=120°， A 为 BE 的中点，延长 BA 到点 P，使 BA=AP，连接 PE （1）求线段 BD 的长 （2）求证：直线 PE 是⊙O 的切线. （2018 荆门）23.如图，AB 为 O 的直径，C 为 O 上一点，经过点C 的切线交 AB 的延长线于点 E ，AD EC 交 EC 的延长线于点 D ， AD 交 O 于 F ， FM AB 于 H ，分别交 O 、 AC 于 M 、 N ，连接 MB ， BC . （1）求证： AC 平方 DAE ； （2）若 4cos 5M  ， 1BE  ，①求 O 的半径；②求 FN 的长. 23.（1）证明：连接 OC ， ∵直线 DE 与 O 相切于点C ， ∴OC DE ， 又∵ AD DE ，∴ / /OC AD . ∴ 1 3   ∵OA OC ，∴ 2 3   ， ∴ 1 2   ， ∴ AC 平方 DAE . （2）解：①∵  BF BF ，∴ DAE M   又∵ / /OC AD ，∴ COE DAE M     ， ∵OC DE ，∴ 90OCE   设 O 的半径为 r ， 则 4cos 1 5 OC OC rOCE OE OB OE r       ，解得 4r  ②连接 BF ， ∵ AB 为 O 的直径，∴ 90AFB   ，∴ 4 32cos 8 5 5AF AB DAE     ， 在 Rt OCE 中， 4 1 5OE r BE     ， 4OC  ，∴ 2 2 2 25 4 3CE OE OC     ， ∵ AB 为 O 的直径，∴ 2 90OBC     ， ∵ 90OCE   ，∴ 90OCB BCE     ， ∵OB OC ，∴ OBC OCB   ，∴ 2 1BCE     ， ∵ AB FM ，∴  AM AF ，∴ 5 4   ， ∵ 90AFB D     ，∴ / /FB DE ，∴ 5 4E     ， ∴ AFN CEB ∽ ， ∴ AF FN CE BE  ，∴ 32 325 3 15 AF BEFN CE    . （2018 淮安）24．（本题满分 10 分） 如图，AB 是⊙O 的直径，AC 是⊙O 的切线，切点为 A，BC 交⊙O 于点 D，点 E 是 AC 的中点． （1）试判断直线 DE 与⊙O 的位置关系，并说明理由； （2）若⊙O 的半径为 2，∠B＝50°，AC＝4.8，求图中阴影部分的面积． （1）先根据“SSS”证明△AEO≌△DEO，从而得到∠ODE＝∠OAE＝90°，即可判断出直线 DE 与⊙O 相切； （2）阴影部分面积为： 24 10 5 9  ． 22．（12 分）（2018 建设兵团）如图，PA 与⊙O 相切于点 A，过点 A 作 AB⊥OP，垂足为 C，交⊙O 于点 B．连接 PB， AO，并延长 AO 交⊙O 于点 D，与 PB 的延长线交于点 E． （1）求证：PB 是⊙O 的切线； （2）若 OC=3，AC=4，求 sinE 的值． （2018 河北）25. 如图 15，点 在数轴上对应的数为 26，以原点 为圆心， 为半径作优弧 ，使点 在 右下方，且 .在优弧 上任取一点 ，且能过 作直线 交数轴于点 ，设 在数轴上对 应的数为 ，连接 . （1）若优弧 上一段 的长为 ，求 的度数及 的值； （2）求 的最小值，并指出此时直线与 所在圆的位置关系； （3）若线段 的长为 ，直接．．写出这时 的值. （2018 北京）22. 如图，AB 是⊙O 的直径，过⊙O 外一点 P 作⊙O 的两条切线 PC，PD，切点分别为 C，D，连接 OP， CD. (1)求证:OP⊥CD; (2)连接 AD，BC，若∠DAB=50°，∠CBA = 70°，OA=2，求 OP 的长. （2018 安顺） 25.如图，在 ABC 中， AB AC ，O 为 BC 的中点， AC 与半圆O 相切于点 D . （1）求证： AB 是半圆O 所在圆的切线； （2）若 2cos 3ABC  ， 12AB  ，求半圆O 所在圆的半径. （2018 遂宁）如图，过⊙O 外一点 P 作⊙O 的切线 PA 切⊙O 于点 A，连接 PO 并延长，与⊙O 交于 C、D 两点，M 是半 圆 CD 的中点，连接 AM 交 CD 于点 N，连接 AC、CM。 （1）求证：CM2=MN•MA （2）若∠P=300，PC=2，求 CM 的长 （2018 仙桃）22．（满分 8 分） 如图，在⊙O 中，AB 为直径，AC 为弦．过 BC 延长线上一点 G，作 GD⊥AO 于点 D，交 AC 于点 E，交⊙O 于点 F， M 是 GE 的中点，连接 CF，CM． （1）判断 CM 与⊙O 的位置关系，并说明理由； （2）若∠ECF  2∠A，CM  6，CF  4，求 MF 的长． （第 22 题图） · A B C DEFMG O （2018 玉林） （2018 河南）19.（9 分）如图，AB 是圆 0 的直径，DO 垂直于点 O，连接 DA 交圆 O 于点 C，过点 C 作圆 O 的切线交 DO 于点 E，连接 BC 交 DO 于点 F。 （1）求证：CE=EF； （2）连接 AF 并延长，交圆 O 于点 G，填空： ①当∠D 的度数为______时，四边形 ECFG 为菱形； ②当∠D 的度数为______时，四边形 ECOG 为正方形。 （2018 广西北部湾经济区） （2018 兰州） （2018 齐齐哈尔） （2018 大庆） （2018 怀化） （2018陕西）23．（本题满分8分） 如图，在 Rt△ABC 中，∠ACB＝90°，以斜边 AB 上的中线 CD 为直径作⊙O，分别与 AC、BC 相交于点 M、N． (1)过点 N 作⊙O 的切线 NE 与 AB 相交于点 E，求证：NE⊥AB； (2)连接 MD，求证：MD＝NB． 23 题图 23 题解图(1) 解：(1)如图，连接 ON ∵CD 是 Rt△ABC 斜边 AB 上的中线 ∴AD＝CD＝DB ∴∠DCB＝∠DBC 又∵∠DCB＝∠ONC ∴∠ONC＝∠DBC ∴ON∥AB ∵NE 是⊙O 的切线，ON 是⊙O 的半径 ∴∠ONE＝90° ∴∠NEB＝90°，即 NE⊥AB； (2)如解图(1)所示，由(1)可知 ON∥AB， O 为⊙O 的圆心，∴OC＝OB，∠CMD＝90° ∴CN＝NB＝1 2 CB，MD∥CB 又∵D 是 AB 的中点，∴MD＝1 2 CB ∴MD＝NB． （2018 长春） （2018 沈阳） （2018 东营）22．(本题满分 8 分)如图，CD 是⊙O 的切线，点 C 在直径 AB 的延长线上． （1）求证：∠CAD=∠BDC； （2）若 BD= 3 2 AD，AC=3，求 CD 的长． 22．(本题满分 8 分) （1）证明：连接 OD ∵OB=OD ∴∠OBD=∠ODB…………………………1 分 ∵CD 是⊙O 的切线，OD 是⊙O 的半径 ∴∠ODB+∠BDC=90°……………………2 分 ∵AB 是⊙O 的直径 ∴∠ADB=90° ∴∠OBD +∠CAD = 90°………………………………………3 分 ∴∠CAD=∠BDC………………………………………………4 分 （2）解:∵∠C=∠C，∠CAD=∠BDC ∴△CDB ∽ △CAD………………………………………………5 分 ∴ AC CD AD BD  …………………………………………………6 分   ∵ 3 2 AD BD ∴ 3 2 AC CD …………………………………………………7 分 ∵ AC=3 ∴ CD=2…………………………………………………8 分 （2018 烟台） （2018 陕西） （2018 南京）27.结果如此巧合！ 下面是小颖对一道题目的解答. 题目：如图， Rt ABC△ 的内切圆与斜边 AB 相切于点 D ， 3AD  ， 4BD  ，求 ABC△ 的面积. 解：设 ABC△ 的内切圆分别与 AC 、 BC 相切于点 E 、 F ，CE 的长为 x . 根据切线长定理，得 3AE AD  ， 4BF BD  ，CF CE x  . 根据勾股定理，得     2 2 23 4 3 4x x     . 整理，得 2 7 12x x  . 所以 1 2ABCS AC BC △   1 3 42 x x    21 7 122 x x    1 12 122    12 . 小颖发现12恰好就是3 4 ，即 ABC△ 的面积等于 AD 与 BD 的积.这仅仅是巧合吗? 请你帮她完成下面的探索. 已知： ABC△ 的内切圆与 AB 相切于点 D ， AD m ， BD n . 可以一般化吗？ （1）若 90C   ，求证： ABC△ 的面积等于 mn . 倒过来思考呢？ （2）若 2AC BC mn  ，求证 90C   . 改变一下条件…… （3）若 60C   ，用 m 、 n 表示 ABC△ 的面积. （2018 桂林）25.（本题满分 10 分）如图 1，已知⊙O 是ΔADB 的外接圆，∠ADB 的平分线 DC 交 AB 于点 M，交⊙O 于点 C，连接 AC，BC. （1）求证：AC=BC； （2）如图 2，在图 1 的基础上做⊙O 的直径 CF 交 AB 于点 E，连接 AF，过点 A 做⊙O 的切线 AH，若 AH//BC，求∠ACF 的度数； （3）在（2）的条件下，若ΔABD 的面积为 36 ，ΔABD 与ΔABC 的面积比为 2：9，求 CD 的长. 25. （本题 10 分） （1）∵DC 平 分 ∠ADB ∴∠ADC=∠BDC ∴AC=BC （2）连接 AO 并延长交 BC 于 I 交⊙O 于 J ∵AH 是⊙O 的切线且 AH∥BC ∴AI⊥BC ∵垂径定理 ∴BI=IC ∵AC=BC ∴IC= 2 1 AC ∴∠IAC=30° ∴∠ABC=60°=∠F=∠ACB ∵FC 是直径 ∴∠FAC=90° ∴∠ACF=180°-90°-60°=30° （3）过点 D 作 ABDG  ，连接 AO 由（1）（2）知 ABC 为等边三角形 ∵∠ACF=30° ∴ CFAB  ∴AE=BE ∴ 3274 3 2 ΔABC  ABS ∴AB= 36 ∴ 33AE 在 RtΔAEO 中，设 EO=x，则 AO=2x ∴ 222 OEAEAO  ∴ 222 )33()2( xx  ∴x=6，⊙O 的半径为 6 ∴CF=12 ∵ 362 1362 1 ΔABD  DGDGABS ∴DG=2 过点 D 作 CFDG ' ,连接 OD ∵ CFAB  , ABDG  ∴CF//DG ∴四边形 G’DGE 为矩形 ∴ 2' EG 11236''  CEEGCG 在 RtΔ DOG' 中 6,5'  ODOG ∴ 11' DG ∴ 3321111 22'2'  CGDGCD (2018 通辽) （2018 昆明） （2018 云南） （2018 曲靖） （2018 毕节）26.(本题 14 分)如图,在△ABC 中,以 BC 为直径的⊙O 交 AC 于点 E,过点 E 作 AB 的垂线交 AB 于点 F, 交 CB 的延长线于点 G,且∠ABG=2∠G. (1)求证:EG 是⊙O 的切线； (2)若 2 1tan C ，AC=8，求⊙O 的半径。 （2018 铜仁） （2018 广安） （2018 资阳） （2018 苏州） （2018 赤峰） （2018 上海）