- 2021-05-11 发布 |
- 37.5 KB |
- 77页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2017中考数学试题汇编四边形含答案解析
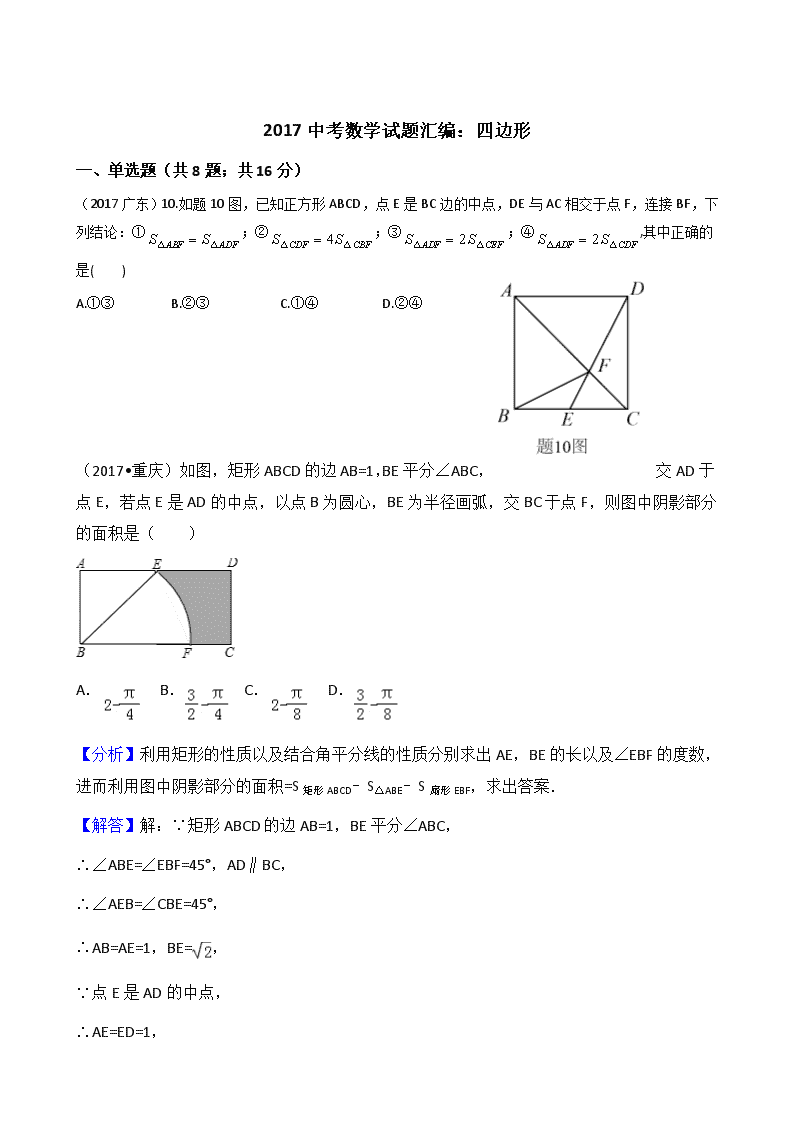
2017中考数学试题汇编:四边形 一、单选题(共8题;共16分) (2017广东)10.如题10图,已知正方形ABCD,点E是BC边的中点,DE与AC相交于点F,连接BF,下列结论:①;②;③;④,其中正确的是( )21世纪教育网版权所有 A.①③ B.②③ C.①④ D.②④ (2017•重庆)如图,矩形ABCD的边AB=1,BE平分∠ABC,交AD于点E,若点E是AD的中点,以点B为圆心,BE为半径画弧,交BC于点F,则图中阴影部分的面积是( ) A. B. C. D. 【分析】利用矩形的性质以及结合角平分线的性质分别求出AE,BE的长以及∠EBF的度数,进而利用图中阴影部分的面积=S矩形ABCD﹣S△ABE﹣S扇形EBF,求出答案. 【解答】解:∵矩形ABCD的边AB=1,BE平分∠ABC, ∴∠ABE=∠EBF=45°,AD∥BC, ∴∠AEB=∠CBE=45°, ∴AB=AE=1,BE=, ∵点E是AD的中点, ∴AE=ED=1, ∴图中阴影部分的面积=S矩形ABCD﹣S△ABE﹣S扇形EBF =1×2﹣×1×1﹣ =﹣. 故选:B. 【点评】此题主要考查了扇形面积求法以及矩形的性质等知识,正确得出BE的长以及∠EBC的度数是解题关键. (2017福建)5.下列关于图形对称性的命题,正确的是( ) A.圆既是轴对称性图形,又是中心对称图形 B.正三角形既是轴对称图形,又是中心对称图形 C.线段是轴对称图形,但不是中心对称图形[来源@:zzs*te%#^p.com] D.菱形是中心对称图形,但不是轴对称图形 【答案】A 点睛:本题主要考查中心对称图形与轴对称图形的知识,能正确地区分是解题的关键.[来#源:中^%教&网@] (2017•台湾)已知坐标平面上有一长方形ABCD,其坐标分别为A(0,0),B(2,0),C(2,1),D(0,1),今固定B点并将此长方形依顺时针方向旋转,如图所示.若旋转后C点的坐标为(3,0),则旋转后D点的坐标为何( ) A.(2,2) B.(2,3) C.(3,3) D.(3,2) 【分析】先根据旋转后C点的坐标为(3,0),得出点C落在x轴上,再根据AC=3,DC=2,即可得到点D的坐标为(3,2). 【解答】解:∵旋转后C点的坐标为(3,0), ∴点C落在x轴上, ∴此时AC=3,DC=2, ∴点D的坐标为(3,2), 故选:D. 【点评】本题主要考查了旋转的性质以及矩形的性质的运用,解题时注意:矩形的四个角都是直角,对边相等. (2017•台湾)如图为互相垂直的两直线将四边形ABCD分成四个区域的情形,若∠A=100°,∠B=∠D=85°,∠C=90°,则根据图中标示的角,判断下列∠1,∠2,∠3的大小关系,何者正确( ) A.∠1=∠2>∠3 B.∠1=∠3>∠2 C.∠2>∠1=∠3 D.∠3>∠1=∠2 【分析】根据多边形的内角和与外角和即可判断. 【解答】解:∵(180°﹣∠1)+∠2=360°﹣90°﹣90°=180° ∴∠1=∠2 ∵(180°﹣∠2)+∠3=360°﹣85°﹣90°=185° ∴∠3﹣∠2=5°, ∴∠3>∠2 ∴∠3>∠1=∠2 故选(D) 【点评】本题考查多边形的内角与外角,解题的关键是熟练运用多边形的内角和与外角和,本题属于基础题型. (2017•台湾)如图为两正方形ABCD,BPQR重叠的情形,其中R点在AD上,CD与QR相交于S点.若两正方形ABCD、BPQR的面积分别为16、25,则四边形RBCS的面积为何( ) A.8 B. C. D. 【分析】根据正方形的边长,根据勾股定理求出AR,求出△ABR∽△DRS,求出DS,根据面积公式求出即可. 【解答】解:∵正方形ABCD的面积为16,正方形BPQR面积为25, ∴正方形ABCD的边长为4,正方形BPQR的边长为5, 在Rt△ABR中,AB=4,BR=5,由勾股定理得:AR=3, ∵四边形ABCD是正方形, ∴∠A=∠D=∠BRQ=90°, ∴∠ABR+∠ARB=90°,∠ARB+∠DRS=90°, ∴∠ABR=∠DRS, ∵∠A=∠D, ∴△ABR∽△DRS, ∴ = , ∴ = , ∴DS= , ∴阴影部分的面积S=S正方形ABCD﹣S△ABR﹣S△RDS=4×4﹣ ﹣1× × = , 故选D. 【点评】本题考查了正方形的性质,相似三角形的性质和判定,能求出△ABR和△RDS的面积是解此题的关键. (2017广西)5.下列图形中不是中心对称图形的是( ) A. B. C. D. 【答案】B. (2017广西)12.如图,在菱形ABCD中,∠ABC=60°,AB=4,点E是AB边上的动点,过点B作直线CE的垂线,垂足为F,当点E从点A运动到点B时,点F的运动路径长为( )www-2-1-cnjy-com A. B.2 C. D. (2017江西)6.如图,任意四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA上的点,对于四边形EFGH的形状,某班学生在一次数学活动课中,通过动手实践,探索出如下结论,其中错误的是( ) A.当E,F,G,H是各边中点,且AC=BD时,四边形EFGH为菱形 B.当E,F,G,H是各边中点,且AC⊥BD时,四边形EFGH为矩形 C.当E,F,G,H不是各边中点时,四边形EFGH可以为平行四边形 D.当E,F,G,H不是各边中点时,四边形EFGH不可能为菱形 【考点】LN:中点四边形. 【分析】连接四边形各边中点所得的四边形必为平行四边形,根据中点四边形的性质进行判断即可. 【解答】解:A.当E,F,G,H是各边中点,且AC=BD时,EF=FG=GH=HE,故四边形EFGH为菱形,故A正确; B.当E,F,G,H是各边中点,且AC⊥BD时,∠EFG=∠FGH=∠GHE=90°,故四边形EFGH为矩形,故B正确; C.当E,F,G,H不是各边中点时,EF∥HG,EF=HG,故四边形EFGH为平行四边形,故C正确; D.当E,F,G,H不是各边中点时,四边形EFGH可能为菱形,故D错误; 故选:D. (2017湖南)8.(3分)如图,在四边形ABCD中,AB∥CD,要使四边形ABCD是平行四边形,可添加的条件不正确的是( ) A.AB=CD B.BC∥AD C.∠A=∠C D.BC=AD 【分析】根据平行四边形的判定方法,逐项判断即可. 【解答】解:∵AB∥CD, ∴当AB=CD时,由一组对边平行且相等的四边形为平行四边形可知该条件正确; 当BC=AD时,该四边形可能为等腰梯形,故该条件不正确; 当∠A=∠C时,可求得∠B=∠D,由两组对角分别相等的四边形为平行四边形可知该条件正确; 当BC∥AD时,由两组对边分别的四边形为平行四边形可知该条件正确; 故选D. 【点评】本题主要考查平行四边形的判定,掌握平行四边形的判定方法是解题的关键. (2017湖南)11.(3分)菱形的两条对角线分别是12和16,则此菱形的边长是( ) A.10 B.8 C.6 D.5 【分析】首先根据题意画出图形,然后由菱形的两条对角线的长分別为12cm和16cm,求得OA与OB,再由勾股定理即可求得菱形的边长. 【解答】解:如图, ∵菱形ABCD中,AC=12,BD=16, ∴OA=AC=6,OB=BD=8,AC⊥BD, ∴AB==10. 即菱形的边长是10. 故选A. 【点评】此题考查了菱形的性质以及勾股定理.掌握菱形的对角线互相平分且垂直是解题的关键. (2017江西)8.(3分)如图,在矩形纸片ABCD中,AB=3,点E在边BC上,将△ABE沿直线AE折叠,点B恰好落在对角线AC上的点F处,若∠EAC=∠ECA,则AC的长是( ) A. B.6 C.4 D.5 【分析】根据折叠的性质得到AF=AB,∠AFE=∠B=90°,根据等腰三角形的性质得到AF=CF,于是得到结论. 【解答】解:∵将△ABE沿直线AE折叠,点B恰好落在对角线AC上的点F处, ∴AF=AB,∠AFE=∠B=90°, ∴EF⊥AC, ∵∠EAC=∠ECA, ∴AE=CE, ∴AF=CF, ∴AC=2AB=6, 故选B. 【点评】本题考查了翻折变换的性质,矩形的性质,熟练掌握折叠的性质是解题的关键. (2017山东)13.(3分)如图,正方形ABCD的对角线AC,BD相交于点O,AB=3,E为OC上一点,OE=1,连接BE,过点A作AF⊥BE于点F,与BD交于点G,则BF的长是( ) A. B.2 C. D. 【分析】根据正方形的性质、全等三角形的判定定理证明△GAO≌△EBO,得到OG=OE=1,证明△BFG∽△BOE,根据相似三角形的性质计算即可. 【解答】解:∵四边形ABCD是正方形,AB=3, ∴∠AOB=90°,AO=BO=CO=3, ∵AF⊥BE, ∴∠EBO=∠GAO, 在△GAO和△EBO中, , ∴△GAO≌△EBO, ∴OG=OE=1, ∴BG=2, 在Rt△BOE中,BE==, ∵∠BFG=∠BOE=90°,∠GBF=∠EBO, ∴△BFG∽△BOE, ∴=,即=, 解得,BF=, 故选:A. 【点评】本题考查的是正方形的性质、全等三角形的判定和性质以及相似三角形的判定和性质,掌握相关的判定定理和性质定理是解题的关键. (23017四川)10.(3分)如图,正方形ABCD中.点E,F分别在BC,CD上,△AEF是等边三角形.连接AC交EF于点G.过点G作GH⊥CE于点H,若S△EGH=3,则S△ADF=( ) A.6 B.4 C.3 D.2 【分析】通过条件可以得出△ABE≌△ADF,从而得出∠BAE=∠DAF,BE=DF,由正方形的性质就可以得出EC=FC,就可以得出AC垂直平分EF,得到EG=GF,根据相似三角形的性质得到S△EFC=12,设AD=x,则DF=x﹣2,根据勾股定理得到AD=+3,DF=3﹣,根据三角形的面积公式即可得到结论. 【解答】解:∵四边形ABCD是正方形, ∴AB=BC=CD=AD,∠B=∠BCD=∠D=∠BAD=90°. ∵△AEF等边三角形, ∴AE=EF=AF,∠EAF=60°. ∴∠BAE+∠DAF=30°. 在Rt△ABE和Rt△ADF中, , ∴Rt△ABE≌Rt△ADF(HL), ∴BE=DF, ∵BC=CD, ∴BC﹣BE=CD﹣DF,即CE=CF, ∴△CEF是等腰直角三角形, ∵AE=AF, ∴AC垂直平分EF, ∴EG=GF, ∵GH⊥CE, ∴GH∥CF, ∴△EGH∽△EFC, ∵S△EGH=3, ∴S△EFC=12, ∴CF=2,EF=4, ∴AF=4, 设AD=x,则DF=x﹣2, ∵AF2=AD2+DF2, ∴(4)2=x2+(x﹣2)2, ∴x=+3, ∴AD=+3,DF=3﹣, ∴S△ADF=AD•DF=6. 故选A. 【点评】本题考查了正方形的性质的运用,全等三角形的判定及性质的运用,相似三角形的判定和性质,勾股定理的运用,等边三角形的性质的运用,解答本题的关键是运用勾股定理的性质. (2017四川)16.(4分)如图1,E为矩形ABCD的边AD上一点,点P从点B出发沿折线BE﹣ED﹣DC运动到点C停止,点Q从点B出发沿BC运动到点C停止,它们运动的速度都是1cm/s.若点P、点Q同时开始运动,设运动时间为t(s),△BPQ的面积为y(cm2),已知y与t之间的函数图象如图2所示. 给出下列结论:①当0<t≤10时,△BPQ是等腰三角形;②S△ABE=48cm2;③当14<t<22时,y=110﹣5t;④在运动过程中,使得△ABP是等腰三角形的P点一共有3个;⑤△BPQ与△ABE相似时,t=14.5. 其中正确结论的序号是 ①③⑤ . 【分析】由图2可知,在点(10,40)至点(14,40)区间,△BPQ的面积不变,因此可推论BC=BE,由此分析动点P的运动过程如下: (1)在BE段,BP=BQ;持续时间10s,则BE=BC=10;y是t的二次函数; (2)在ED段,y=40是定值,持续时间4s,则ED=4; (3)在DC段,y持续减小直至为0,y是t的一次函数. 【解答】解:由图象可以判定:BE=BC=10 cm.DE=4 cm, 当点P在ED上运动时,S△BPQ=BC•AB=40cm2, ∴AB=8 cm, ∴AE=6 cm, ∴当0<t≤10时,点P在BE上运动,BP=BQ, ∴△BPQ是等腰三角形, 故①正确; S△ABE=AB•AE=24 cm2, 故②错误; 当14<t<22时,点P在CD上运动,该段函数图象经过(14,40)和(22,0)两点,解析式为y=110﹣5t, 故③正确; △ABP为等腰三角形需要分类讨论:当AB=AP时,ED上存在一个符号题意的P点,当BA=BO时,BE上存在一个符合同意的P点,当PA=PB时,点P在AB垂直平分线上,所以BE和CD上各存在一个符号题意的P点,共有4个点满足题意, 故④错误; ⑤△BPQ与△ABE相似时,只有;△BPQ∽△BEA这种情况,此时点Q与点C重合,即==, ∴PC=7.5,即t=14.5. 故⑤正确. 综上所述,正确的结论的序号是①③⑤. 故答案是:①③⑤. 【点评】本题考查动点问题的函数图象,需要结合几何图形与函数图象,认真分析动点的运动过程.突破点在于正确判断出BC=BE=10cm. (2017新疆)9.(4分)(2017•乌鲁木齐)如图,在矩形ABCD中,点F在AD上,点E在BC上,把这个矩形沿EF折叠后,使点D恰好落在BC边上的G点处,若矩形面积为4且∠AFG=60°,GE=2BG,则折痕EF的长为( ) A.1 B. C.2 D. 【分析】由折叠的性质可知,DF=GF、HE=CE、GH=DC、∠DFE=∠GFE,结合∠AFG=60°即可得出∠GFE=60°,进而可得出△GEF为等边三角形,在Rt△GHE中,通过解含30度角的直角三角形及勾股定理即可得出GE=2EC、DC=EC,再由GE=2BG结合矩形面积为4,即可求出EC的长度,根据EF=GE=2EC即可求出结论. 【解答】解:由折叠的性质可知,DF=GF,HE=CE,GH=DC,∠DFE=∠GFE. ∵∠GFE+∠DFE=180°﹣∠AFG=120°, ∴∠GFE=60°. ∵AF∥GE,∠AFG=60°, ∴∠FGE=∠AFG=60°, ∴△GEF为等边三角形, ∴EF=GE. ∵∠FGE=60°,∠FGE+∠HGE=90°, ∴∠HGE=30°. 在Rt△GHE中,∠HGE=30°, ∴GE=2HE=CE, ∴GH==HE=CE. ∵GE=2BG, ∴BC=BG+GE+EC=4EC. ∵矩形ABCD的面积为4, ∴4EC•EC=4, ∴EC=1,EF=GE=2. 故选C. 【点评】本题考查了翻折变换、矩形的性质、等边三角形的判定及性质以及解含30度角的直角三角形,根据边角关系及解直角三角形找出BC=4EC、DC=EC是解题的关键. (2017河北)9.求证:菱形的两条对角线互相垂直. 已知:如图,四边形是菱形,对角线,交于点. 求证:. 以下是排乱的证明过程:①又, ②∴,即. ③∵四边形是菱形, ④∴. 证明步骤正确的顺序是( ) A.③→②→①→④ B.③→④→①→② C.①→②→④→③ D.①→④→③→② (2017河北)11.如图是边长为10的正方形铁片,过两个顶点剪掉一个三角形,以下四种剪法中,裁剪线长度所标的数据(单位:)不正确的( ) (2017河南)7.如图,在中,对角线,相交于点,添加下列条件不能判定是菱形的只有( ) A. B. C. D. (2017河南)9.我们知道:四边形具有不稳定性.如图,在平面直角坐标系中,边长为2的正方形的边在轴上,的中点是坐标原点固定点,,把正方形沿箭头方向推,使点落在轴正半轴上点处,则点的对应点的坐标为( ) A. B. C. D. (2017内蒙古)9.如图,四边形是边长为1的正方形,,为所在直线上的两点,若,,则以下结论正确的是( )[来源:学*科*网] A. B. C. D.四边形的面积为 (2017山西)10.右图是某商品的标志图案,与是的两条直径,首尾顺次连接点,得到四边形.若,则图中阴影部分的面积为( ) A. B. C. D. (2017·衢州)如图,矩形纸片ABCD中,AB=4,BC=6,将△ABC沿AC折叠,使点B落在点E处,CE交AD于点F,则DF的长等于( ) A、 B、 C、 D、 (2017•温州)四个全等的直角三角形按图示方式围成正方形ABCD,过各较长直角边的中点作垂线,围成面积为S的小正方形EFGH.已知AM为Rt△ABM较长直角边,AM=2 EF,则正方形ABCD的面积为( ) A、12S B、10S C、9S D、8S (2017•绍兴)在探索“尺规三等分角”这个数学名题的过程中,曾利用了如图,该图中,四边形ABCD是矩形,E是BA延长线上一点,F是CE上一点,∠ACF=∠AFC,∠FAE=∠FEA。若∠ACB=21°,则∠ECD 的度数是( ) A、7° B、21° C、23° D、24° (2017·嘉兴)一张矩形纸片 ,已知 , ,小明按所给图步骤折叠纸片,则线段 长为( ) A、 B、 C、 D、 (2017·嘉兴)如图,在平面直角坐标系 中,已知点 , .若平移点 到点 ,使以点 , , , 为顶点的四边形是菱形,则正确的平移方法是( ) A、向左平移1个单位,再向下平移1个单位 B、向左平移 个单位,再向上平移1个单位 C、向右平移 个单位,再向上平移1个单位 D、向右平移1个单位,再向上平移1个单位 (2017·丽水)如图,在□ABCD中,连结AC,∠ABC=∠CAD=45°,AB=2,则BC的长是( ) A、 B、2 C、2 D、4 (2017•宁波)如图,四边形ABCD是边长为6的正方形,点E在边AB上,BE=4,过点E作EF∥BC,分别交BD、CD于G、F两点.若M、N分别是DG、CE的中点,则MN的长为 ( ) A、3 B、 C、 D、4 (2017·台州)如图,矩形EFGH四个顶点分别在菱形ABCD的四条边上,BE=BF,将△AEH,△CFG分别沿边EH,FG折叠,当重叠部分为菱形且面积是菱形ABCD面积的 时,则 为( ) A、 B、2 C、 D、4 二、填空题(共6题;共7分) (2017天津)17.如图,正方形和正方形的边长分别为3和1,点分别在边上,为的中点,连接,则的长为 .w (2017广东)16.如题16图(1),矩形纸片ABCD中,AB=5,BC=3,先按题16图(2)操作,将矩形纸片ABCD沿过点A的直线折叠,使点D落在边AB上的点E处,折痕为AF;再按题16图(3)操作:沿过点F的直线折叠,使点C落在EF上的点H处,折痕为FG,则A、H两点间的距离为 .2 (2017广西)17.如图,在矩形ABCD中,对角线AC,BD交于点O,过点A作EA⊥CA交DB的延长线于点E,若AB=3,BC=4,则的值为 .21*cnjy*com 【答案】. (2017黑龙江)20.如图,在矩形ABCD中,M为BC边上一点,连接AM,过点D作DE⊥AM,垂足为E.若DE=DC=1,AE=2EM,则BM的长为 . (2017吉林)11.如图,在矩形ABCD中,AB=5,AD=3.矩形ABCD绕着点A逆时针旋转一定角度得到矩形AB'C'D'.若点B的对应点B'落在边CD上,则B'C的长为 . 【答案】1. 【解析】 试题解析:由旋转的性质得到AB=AB′=5, 在直角△AB′D中,∠D=90°,AD=3,AB′=AB=5, 所以B′D==4, 所以B′C=5﹣B′D=1. 故答案是:1. 考点:旋转的性质;矩形的性质. (2017贵州)15.(4分)已知菱形的两条对角线的长分别是5cm,6cm,则菱形的面积是 cm2. (2017湖南)18.(3分)正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图所示放置,点A1,A2,A3和C1,C2,C3,…分别在直线y=x+1和x轴上,则点 B2018的纵坐标是 22017 . 【分析】根据一次函数图象上点的坐标特征结合正方形的性质即可得出点B1、B2、B3、…的坐标,根据点坐标的变化找出点Bn的坐标,依此即可得出结论. 【解答】解:当x=0时,y=x+1=1, ∴点A1的坐标为(0,1). ∵A1B1C1O为正方形, ∴点C1的坐标为(1,0),点B1的坐标为(1,1). 同理,可得:B2(3,2),B3(7,4),B4(15,8), ∴点Bn的坐标为(2n﹣1,2n﹣1), ∴点B2018的坐标为(22018﹣1,22017). 故答案为:22017. 【点评】本题考查了一次函数图象上点的坐标特征、正方形的性质以及规律型中点的坐标,根据点坐标的变化找出变化规律“点Bn的坐标为(2n﹣1,2n﹣1)”是解题的关键. (2017辽宁)16.(3分)如图,在矩形ABCD中,AB=5,BC=3,将矩形ABCD绕点B按顺时针方向旋转得到矩形GBEF,点A落在矩形ABCD的边CD上,连接CE,则CE的长是 . 【分析】连接AG,根据旋转变换的性质得到,∠ABG=∠CBE,BA=BG,根据勾股定理求出CG、AD,根据相似三角形的性质列出比例式,计算即可. 【解答】解:连接AG, 由旋转变换的性质可知,∠ABG=∠CBE,BA=BG=5,BC=BE, 由勾股定理得,CG==4, ∴DG=DC﹣CG=1, 则AG==, ∵=,∠ABG=∠CBE, ∴△ABG∽△CBE, ∴==, 解得,CE=, 故答案为:. 【点评】本题考查的是翻转变换的性质、相似三角形的判定和性质,掌握勾股定理、矩形的性质、旋转变换的性质是解题的关键. (2017重庆)18.(4分)(2017•重庆)如图,正方形ABCD中,AD=4,点E是对角线AC上一点,连接DE,过点E作EF⊥ED,交AB于点F,连接DF,交AC于点G,将△EFG沿EF翻折,得到△EFM,连接DM,交EF于点N,若点F是AB的中点,则△EMN的周长是 . 【分析】如图1,作辅助线,构建全等三角形,根据全等三角形对应边相等证明FQ=BQ=PE=1,△DEF是等腰直角三角形,利用勾理计算DE=EF=,PD==3,如图2,由平行相似证明△DGC∽△FGA,列比例式可得FG和CG的长,从而得EG的长,根据△GHF是等腰直角三角形,得GH和FH的长,利用DE∥GM证明△DEN∽△MNH,则,得EN=,从而计算出△EMN各边的长,相加可得周长. 【解答】解:如图1,过E作PQ⊥DC,交DC于P,交AB于Q,连接BE, ∵DC∥AB, ∴PQ⊥AB, ∵四边形ABCD是正方形, ∴∠ACD=45°, ∴△PEC是等腰直角三角形, ∴PE=PC, 设PC=x,则PE=x,PD=4﹣x,EQ=4﹣x, ∴PD=EQ, ∵∠DPE=∠EQF=90°,∠PED=∠EFQ, ∴△DPE≌△EQF, ∴DE=EF, 易证明△DEC≌△BEC, ∴DE=BE, ∴EF=BE, ∵EQ⊥FB, ∴FQ=BQ=BF, ∵AB=4,F是AB的中点, ∴BF=2, ∴FQ=BQ=PE=1, ∴CE=, Rt△DAF中,DF==2, ∵DE=EF,DE⊥EF, ∴△DEF是等腰直角三角形, ∴DE=EF==, ∴PD==3, 如图2,∵DC∥AB, ∴△DGC∽△FGA, ∴==2, ∴CG=2AG,DG=2FG, ∴FG=×=, ∵AC==4, ∴CG=×=, ∴EG=﹣=, 连接GM、GN,交EF于H, ∵∠GFE=45°, ∴△GHF是等腰直角三角形, ∴GH=FH==, ∴EH=EF﹣FH=﹣=, 由折叠得:GM⊥EF,MH=GH=, ∴∠EHM=∠DEF=90°, ∴DE∥HM, ∴△DEN∽△MNH, ∴, ∴==3, ∴EN=3NH, ∵EN+NH═EH=, ∴EN=, ∴NH=EH﹣EN=﹣=, Rt△GNH中,GN===, 由折叠得:MN=GN,EM=EG, ∴△EMN的周长=EN+MN+EM=++=; 故答案为:. 【点评】本题考查了正方形的性质、翻折变换的性质、三角形全等、相似的性质和判定、勾股定理,三角函数,计算比较复杂,作辅助线,构建全等三角形,计算出PE的长是关键. (2017内蒙古)15.如图,在中,,,是两条对角线的交点,过点作的垂线分别交边,于点,,点是边的一个三等分点,则与的面积比为 . (2017•温州)如图,矩形OABC的边OA,OC分别在x轴、y轴上,点B在第一象限,点D在边BC上,且∠AOD=30°,四边形OA′B′D与四边形OABD关于直线OD对称(点A′和A,B′和B分别对应).若AB=1,反比例函数y= (k≠0)的图象恰好经过点A′,B,则k的值为________. (2017•绍兴)如图为某城市部分街道示意图,四边形ABCD为正方形,点G在对角线BD上,GE⊥CD,GF⊥BC,AD=1500m,小敏行走的路线为B→A→G→E,小聪得行走的路线为B→A→D→E→F.若小敏行走的路程为3100m,则小聪行走的路程为________m. (2017·丽水)我国三国时期数学家赵爽为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”,如图1所示.在图2中,若正方形ABCD的边长为14,正方形IJKL的边长为2,且IJ//AB,则正方形EFGH 的边长为________. (2017•宁波)如图,在菱形纸片ABCD中,AB=2,∠A=60°,将菱形纸片翻折,使点A落在CD的中点E处,折痕为FG,点F、G分别在边AB、AD上.则cos∠EFG的值为________. (2017·台州)如图,有一个不定的正方形ABCD,它的两个相对的顶点A,C分别在边长为1的正六边形一组对边上,另外两个顶点B,D在正六边形内部(包括边界),则正方形边长a的取值范围是________ (2017·金华)在一空旷场地上设计一落地为矩形ABCD的小屋,AB+BC=10m.拴住小狗的10m长的绳子一端固定在B点处,小狗在不能进入小屋内的条件下活动,其可以活动的区域面积为S(m2). ①如图1,若BC=4m,则S=________m. ②如图2,现考虑在(1)中的矩形ABCD小屋的右侧以CD为边拓展一正△CDE区域,使之变成落地为五边形 ABCED的小屋,其它条件不变.则在BC的变化过程中,当S取得最小值时,边BC的长为________m. 三、解答题(共11题;共138分) (2017北京)22.(5分)如图,在四边形ABCD中,BD为一条对角线,AD∥BC,AD=2BC,∠ABD=90°,E为AD的中点,连接BE. (1)求证:四边形BCDE为菱形; (2)连接AC,若AC平分∠BAD,BC=1,求AC的长. 【分析】(1)由DE=BC,DE∥BC,推出四边形BCDE是平行四边形,再证明BE=DE即可解决问题; (2)在Rt△ACD中只要证明∠ADC=60°,AD=2即可解决问题; 【解答】(1)证明:∵AD=2BC,E为AD的中点, ∴DE=BC, ∵AD∥BC, ∴四边形BCDE是平行四边形, ∵∠ABD=90°,AE=DE, ∴BE=DE, ∴四边形BCDE是菱形. (2)解:连接AC. ∵AD∥BC,AC平分∠BAD, ∴∠BAC=∠DAC=∠BCA, ∴AB=BC=1, ∵AD=2BC=2, ∴sin∠ADB=, ∴∠ADB=30°, ∴∠DAC=30°,∠ADC=60°, 在Rt△ACD中,∵AD=2, ∴CD=1,AC=. 【点评】本题考查菱形的判定和性质、直角三角形斜边中线的性质、锐角三角函数等知识,解题的关键是熟练掌握菱形的判定方法,属于中考常考题型. (2017上海)23.已知:如图,四边形ABCD中,AD∥BC,AD=CD,E是对角线BD上一点,且EA=EC. (1)求证:四边形ABCD是菱形; (2)如果BE=BC,且∠CBE:∠BCE=2:3,求证:四边形ABCD是正方形. 【分析】(1)首先证得△ADE≌△CDE,由全等三角形的性质可得∠ADE=∠CDE,由AD∥BC可得∠ADE=∠CBD,易得∠CDB=∠CBD,可得BC=CD,易得AD=BC,利用平行线的判定定理可得四边形ABCD为平行四边形,由AD=CD可得四边形ABCD是菱形; (2)由BE=BC可得△BEC为等腰三角形,可得∠BCE=∠BEC,利用三角形的内角和定理可得∠CBE=180×=45°,易得∠ABE=45°,可得∠ABC=90°,由正方形的判定定理可得四边形ABCD是正方形. 【解答】证明:(1)在△ADE与△CDE中, , ∴△ADE≌△CDE, ∴∠ADE=∠CDE, ∵AD∥BC, ∴∠ADE=∠CBD, ∴∠CDE=∠CBD, ∴BC=CD, ∵AD=CD, ∴BC=AD, ∴四边形ABCD为平行四边形, ∵AD=CD, ∴四边形ABCD是菱形; (2)∵BE=BC ∴∠BCE=∠BEC, ∵∠CBE:∠BCE=2:3, ∴∠CBE=180×=45°, ∵四边形ABCD是菱形, ∴∠ABE=45°, ∴∠ABC=90°, ∴四边形ABCD是正方形. 【点评】本题主要考查了正方形与菱形的判定及性质定理,熟练掌握定理是解答此题的关键. (2017福建)24.如图,矩形中,,分别是线段AC、BC上的点,且四边形为矩形. (Ⅰ)若是等腰三角形时,求的长; (Ⅱ)若,求的长.[www%.zz@s&t~ep.co^m] 【答案】(Ⅰ)AP的长为4或5或;(Ⅱ)CF= 【解析】 试题分析:(Ⅰ)分情况CP=CD、PD=PC、DP=DC讨论即可得; (Ⅱ)连结PF、DE,记PF与DE的交点为O,连结OC,通过证明△ADP∽△CDF,从而得 ,由AP= ,从而可得CF= . 试题解析:(Ⅰ)在矩形ABCD中,AB=6,AD=8,∠ADC=90°,∴DC=AB=6, AC= =10; 要使△PCD是等腰三角形,有如下三种情况: (1)当CP=CD时,CP=6,∴AP=AC-CP=4 ;[来&源:中国^%教@育出版~网] (2)当PD=PC时,∠PDC=∠PCD,∵∠PCD+∠PAD=∠PDC+∠PDA=90°,∴∠PAD=∠PDA,∴PD=PA,∴PA=PC,∴AP= ,即AP=5; (3)当DP=DC时,过D作DQ⊥AC于Q,则PQ=CQ,∵S△ADC= AD·DC= AC·DQ,∴DQ= ,∴CQ= ,∴PC=2CQ = ,∴AP=AC-PC= . 综上所述,若△PCD是等腰三角形,AP的长为4或5或; (Ⅱ)连结PF、DE,记PF与DE的交点为O,连结OC, 点睛:本题主要考查矩形的性质、等腰三角形的判定与性质,相似三角形的判定与性质等,能正确地分情况进行讨论是判定△PCD要等腰三角形的关键.[来源:zz&step%.#co@ (2017广东)21.如图21图所示,已知四边形ABCD、ADEF都是菱形,为锐角. (1)求证:; (2)若BF=BC,求的度数。 (2017吉林)23.如图①,BD是矩形ABCD的对角线,∠ABD=30°,AD=1.将△BCD沿射线BD方向平移到△B'C'D'的位置,使B'为BD中点,连接AB',C'D,AD',BC',如图②. (1)求证:四边形AB'C'D是菱形; (2)四边形ABC'D′的周长为 ; (3)将四边形ABC'D'沿它的两条对角线剪开,用得到的四个三角形拼成与其面积相等的矩形,直接写出所有可能拼成的矩形周长. 【答案】(1)证明见解析;(2)4;(3)6+或2+3. 【解析】 ∴∠ADB=60°, 由平移可得,B'C'=BC=AD,∠D'B'C'=∠DBC=∠ADB=60°, ∴AD∥B'C' ∴四边形AB'C'D是平行四边形, ∵B'为BD中点, ∴Rt△ABD中,AB'=BD=DB', 又∵∠ADB=60°, ∴△ADB'是等边三角形, ∴AD=AB', ∴四边形AB'C'D是菱形; (2)由平移可得,AB=C'D',∠ABD'=∠C'D'B=30°, ∴AB∥C'D', ∴四边形ABC'D'是平行四边形, 由(1)可得,AC'⊥B'D, ∴四边形ABC'D'是菱形, ∵AB=AD=, ∴四边形ABC'D′的周长为4, ∴矩形周长为6+或2+3. 考点:菱形的判定与性质;矩形的性质;图形的剪拼;平移的性质. (2017江西)如图,正方形ABCD中,点E,F,G分别在AB,BC,CD上,且∠EFG=90°.求证:△EBF∽△FCG. 【考点】S8:相似三角形的判定;6A:分式的乘除法;LE:正方形的性质. 【分析】(1)先把分母因式分解,再把除法运算化为乘法运算,然后约分即可; (2)先根据正方形的性质得∠B=∠C=90°,再利用等角的余角相等得∠BEF=∠CFG,然后根据有两组角对应相等的两个三角形相似可判定△EBF∽△FCG. (2017贵州)20.(10分)如图,已知:∠BAC=∠EAD,AB=20.4,AC=48,AE=17,AD=40. 求证:△ABC∽△AED. 【分析】先证得=,然后根据相似三角形的判定定理即可证得结论. 【解答】证明:∵AB=20.4,AC=48,AE=17,AD=40. ∴==1.2,==1.2, ∴=, ∵∠BAC=∠EAD, ∴△ABC∽△AED. 【点评】本题重点考查了相似三角形的判定定理,本题比较简单,注要找准相似的两个三角形就可以了. (2017湖南)27.(12分)如图,正方形ABCD的边长为1,点E为边AB上一动点,连结CE并将其绕点C顺时针旋转90°得到CF,连结DF,以CE、CF为邻边作矩形CFGE,GE与AD、AC分别交于点H、M,GF交CD延长线于点N. (1)证明:点A、D、F在同一条直线上; (2)随着点E的移动,线段DH是否有最小值?若有,求出最小值;若没有,请说明理由; (3)连结EF、MN,当MN∥EF时,求AE的长. 【分析】(1)由△DCF≌△BCE,可得∠CDF=∠B=90°,即可推出∠CDF+∠CDA=180°,由此即可证明. (2)有最小值.设AE=x,DH=y,则AH=1﹣y,BE=1﹣x,由△ECB∽△HEA,推出=,可得=,推出y=x2﹣x+1=(x﹣)2+,由a=1>0,y有最小值,最小值为. (3)只要证明△CFN≌△CEM,推出∠FCN=∠ECM,由∠MCN=45°,可得∠FCN=∠ECM=∠BCE=22.5°,在BC上取一点G,使得GC=GE,则△BGE是等腰直角三角形,设BE=BG=a,则GC=GE=a,可得a+a=1,求出a即可解决问题; 【解答】(1)证明:∵四边形ABCD是正方形, ∴CD=CB,∠BCD=∠B=∠ADC=90°, ∵CE=CF,∠ECF=90°, ∴∠ECF=∠DCB, ∴∠DCF=∠BCE, ∴△DCF≌△BCE, ∴∠CDF=∠B=90°, ∴∠CDF+∠CDA=180°, ∴点A、D、F在同一条直线上. (2)解:有最小值. 理由:设AE=x,DH=y,则AH=1﹣y,BE=1﹣x, ∵四边形CFGE是矩形, ∴∠CEG=90°, ∴∠CEB+∠AEH=90° CEB+∠ECB=90°, ∴∠ECB=∠AEH, ∵∠B=∠EAH=90°, ∴△ECB∽△HEA, ∴=, ∴=, ∴y=x2﹣x+1=(x﹣)2+, ∵a=1>0, ∴y有最小值,最小值为. ∴DH的最小值为. (3)解:∵四边形CFGE是矩形,CF=CE, ∴四边形CFGE是正方形, ∴GF=GE,∠GFE=∠GEF=45°, ∵NM∥EF, ∴∠GNM=∠GFE,∠GMN=∠GEF, ∴∠GMN=∠GNM, ∴GN=GM, ∴FN=EM, ∵CF=CE,∠CFN=∠CEM, ∴△CFN≌△CEM, ∴∠FCN=∠ECM,∵∠MCN=45°, ∴∠FCN=∠ECM=∠BCE=22.5°, 在BC上取一点G,使得GC=GE,则△BGE是等腰直角三角形,设BE=BG=a,则GC=GE=a, ∴a+a=1, ∴a=﹣1, ∴AE=AB﹣BE=1﹣(﹣1)=2﹣. 【点评】本题考查四边形综合题、正方形的性质、等腰直角三角形的性质、全等三角形的判定和性质、相似三角形的判定和性质、勾股定理等知识,解题的关键是灵活应用所学知识解决问题,学会构建二次函数解决最值问题,学会用方程的思想思考问题,属于中考压轴题. (2017江苏)21.(8分)已知:如图,在平行四边形ABCD中,AE⊥BD,CF⊥BD,垂足分别为E,F.求证:△ADE≌△CBF. 【分析】证出∠ADE=∠CBF,AD=CB,由AAS证△ADE≌△CBF即可. 【解答】证明:∵四边形ABCD是平行四边形, ∴AD=CB,AD∥BC, ∴∠ADE=∠CBF, ∵AE⊥BD,CF⊥BD, ∴∠AED=∠CFB=90°, 在△ADE和△CBF中,, ∴△ADE≌△CBF(AAS). 【点评】此题考查了平行四边形的性质、全等三角形的判定.熟练掌握平行四边形的性质是解决问题的关键. (2017辽宁)18.(8分)如图,在菱形ABCD中,过点D作DE⊥AB于点E,作DF⊥BC于点F,连接EF. 求证:(1)△ADE≌△CDF; (2)∠BEF=∠BFE. 【分析】(1)利用菱形的性质得到AD=CD,∠A=∠C,进而利用AAS证明两三角形全等; (2)根据△ADE≌△CDF得到AE=CF,结合菱形的四条边相等即可得到结论. 【解答】证明:(1)∵四边形ABCD是菱形, ∴AD=CD,∠A=∠C, ∵DE⊥BA,DF⊥CB, ∴∠AED=∠CFD=90°, 在△ADE和△CDE, ∵, ∴△ADE≌△CDE; (2)∵四边形ABCD是菱形, ∴AB=CB, ∵△ADE≌△CDF, ∴AE=CF, ∴BE=BF, ∴∠BEF=∠BFE. 【点评】本题主要考查了菱形的性质以及全等三角形的判定与性质,解题的关键是掌握菱形的性质以及AAS证明两三角形全等,此题难度一般. (2017山东)23.(4分)如图,在矩形ABCD,AD=AE,DF⊥AE于点F.求证:AB=DF. 【分析】利用矩形和直角三角形的性质得到∠AEB=∠EAD、∠AFD=∠B,从而证得两个三角形全等,可得结论. 【解答】证明:∵四边形ABCD是矩形, ∴AD∥BC,∠B=90°, ∴∠AEB=∠DAE, ∵DF⊥AE, ∴∠AFD=∠B=90°, 在△ABE和△DFA中 ∵ ∴△ABE≌△DFA, ∴AB=DF. 【点评】本题考查了全等三角形的判定与性质、矩形的性质的知识,属于基础题,难度不是很大,熟练掌握全等三角形的判定与性质是关键. (2017四川)19.(6分)如图,在平行四边形ABCD中,AE⊥BC,CF⊥AD,垂足分别为E,F,AE,CF分别与BD交于点G和H,且AB=2. (1)若tan∠ABE=2,求CF的长; (2)求证:BG=DH. 【分析】(1)由平行四边形的性质,结合三角函数的定义,在Rt△CFD中,可求得CF=2DF,利用勾股定理可求得CF的长; (2)利用平行四边形的性质结合条件可证得△AGD≌△CHB,则可求得BH=DG,从而可证得BG=DH. 【解答】(1)解: ∵四边形ABCD是平行四边形, ∴∠CDF=∠ABE,DC=AB=2, ∵tan∠ABE=2, ∴tan∠CDF=2, ∵CF⊥AD, ∴△CFD是直角三角形, ∴=2, 设DF=x,则CF=2x, 在Rt△CFD中,由勾股定理可得(2x)2+x2=(2)2,解得x=2或x=﹣2(舍去), ∴CF=4; (2)证明: ∵四边形ABCD是平行四边形, ∴AD=BC,AD∥BC, ∴∠ADB=∠CBD, ∵AE⊥BC,CF⊥AD, ∴AE⊥AD,CF⊥BC, ∴∠GAD=∠HCB=90°, ∴△AGD≌△CHB, ∴BH=DG, ∴BG=DH. 【点评】本题主要考查平行四边形的性质,掌握平行四边形的对边平行且相等是解题的关键,注意全等三角形的应用. (2017新疆)19.(10分)(2017•乌鲁木齐)如图,四边形ABCD是平行四边形,E,F是对角线BD上的两点,且BF=ED,求证:AE∥CF. 【分析】连接AC,交BD于点O,由“平行四边形ABCD的对角线互相平分”得到OA=OC,OB=OD;然后结合已知条件证得OE=OF,则“对角线互相平分的四边形是平行四边形”,即可得出结论. 【解答】证明:连接AC,交BD于点O,如图所示: ∵四边形ABCD是平行四边形, ∴OA=OC,OB=OD, ∵BF=ED, ∴OE=OF, ∵OA=OC, ∴四边形AECF是平行四边形, ∴AE∥CF. 【点评】本题考查了平行四边形的判定与性质,平行四边形的判定方法共有五种,应用时要认真领会它们之间的联系与区别,同时要根据条件合理、灵活地选择方法是解决问题的关键. (2017河北)25.平面内,如图,在中,,,.点为边上任意一点,连接,将绕点逆时针旋转得到线段. (1)当时,求的大小; (2)当时,求点与点间的距离(结果保留根号); (3)若点恰好落在的边所在的直线上,直接写出旋转到所扫过的面积(结果保留). (2017山西)17.已知:如图,在中,延长线至点,延长至点,使得.连接,与对角线交于点. 求证:. (2017湖北)19.已知:如图,在中,,点是的中点,点是的中点,点是的中点,过点作交的延长线于点. (1)求证:; (2)若,求的长. (2017•杭州)如图,在正方形ABCD中,点G在对角线BD上(不与点B,D重合),GE⊥DC于点E,GF⊥BC于点F,连结AG. (1)写出线段AG,GE,GF长度之间的数量关系,并说明理由; (2)若正方形ABCD的边长为1,∠AGF=105°,求线段BG的长. (2017•舟山)如图, 是 的中线, 是线段 上一点(不与点 重合). 交 于点 , ,连结 . (1)如图1,当点 与 重合时,求证:四边形 是平行四边形; (2)如图2,当点 不与 重合时,(1)中的结论还成立吗?请说明理由. (3)如图3,延长 交 于点 ,若 ,且 .当 , 时,求 的长. (2017•宁波)在一次课题学习中,老师让同学们合作编题.某学习小组受赵爽弦图的启发,编写了下面这道题,请你来解一解. 如图,将矩形ABCD的四边BA、CB、DC、AD分别延长至E、F、G、H,使得AE=CG,BF=DH,连结EF、FG、GH、HE. (1)求证:四边形EFGH为平行四边形; (2)若矩形ABCD是边长为1的正方形,且∠FEB=45°,tan∠AEH=2,求AE的长. (2017·丽水)如图,在矩形ABCD中,点E是AD上的一个动点,连接BE,作点A关于BE的对称点F,且点F落在矩形ABCD的内部,连结AF,BF,EF,过点F作GF⊥AF交AD于点G,设 =n. (1)求证:AE=GE; (2)当点F落在AC上时,用含n的代数式表示 的值; (3)若AD=4AB,且以点F,C,G为顶点的三角形是直角三角形,求n的值. (2017•温州)小黄准备给长8m,宽6m的长方形客厅铺设瓷砖,现将其划分成一个长方形ABCD区域Ⅰ(阴影部分)和一个环形区域Ⅱ(空白部分),其中区域Ⅰ用甲、乙、丙三种瓷砖铺设,且满足PQ∥AD ,如图所示. (1)若区域Ⅰ的三种瓷砖均价为300元/m2 , 面积为S(m2),区域Ⅱ的瓷砖均价为200元/m2 , 且两区域的瓷砖总价为不超过12000元,求S的最大值; (2)若区域Ⅰ满足AB:BC=2:3,区域Ⅱ四周宽度相等 ①求AB,BC的长; ②若甲、丙两瓷砖单价之和为300元/m2 , 乙、丙瓷砖单价之比为5:3,且区域Ⅰ的三种瓷砖总价为4800元,求丙瓷砖单价的取值范围. (2017•温州)如图,在△ABC中,AC=BC,∠ACB=90°,⊙O(圆心O在△ABC内部)经过B、C两点,交AB于点E,过点E作⊙O的切线交AC于点F.延长CO交AB于点G,作ED∥AC交CG于点D (1)求证:四边形CDEF是平行四边形; (2)若BC=3,tan∠DEF=2,求BG的值. (2017•绍兴)如图1,已知□ABCD,AB//x轴,AB=6,点A的坐标为(1,-4),点D的坐标为(-3,4),点B在第四象限,点P是□ABCD边上的一个动点. (1)若点P在边BC上,PD=CD,求点P的坐标. (2)若点P在边AB,AD上,点P关于坐标轴对称的点Q落在直线y=x-1上,求点P的坐标. (3)若点P在边AB,AD,CD上,点G是AD与y轴的交点,如图2,过点P作y轴的平行线PM,过点G作x轴的平行线GM,它们相交于点M,将△PGM沿直线PG翻折,当点M的对应点落在坐标轴上时,求点P的坐标(直接写出答案). (2017•绍兴)定义:有一组邻边相等,并且它们的夹角是直角的凸四边形叫做等腰直角四边形. (1)如图1,等腰直角四边形ABCD,AB=BC,∠ABC=90°, ①若AB=CD=1,AB//CD,求对角线BD的长. ②若AC⊥BD,求证:AD=CD. (2)如图2,在矩形ABCD中,AB=5,BC=9,点P是对角线BD上一点,且BP=2PD,过点P作直线分别交边AD,BC于点E,F,使四边形ABFE是等腰直角四边形.求AE的长. 23、(2017·衢州)在直角坐标系中,过原点O及点A(8,0),C(0,6)作矩形OABC,连结OB,D为OB的中点。点E是线段AB上的动点,连结DE,作DF⊥DE,交OA于点F,连结EF。已知点E从A点出发,以每秒1个单位长度的速度在线段AB上移动,设移动时间为t秒。 (1)如图1,当t=3时,求DF的长; (2)如图2,当点E在线段AB上移动的过程中,∠DEF的大小是否发生变化?如果变化,请说明理由;如果不变,请求出tan∠DEF的值; (3)连结AD,当AD将△DEF分成的两部分面积之比为1:2时,求相应t的值。 (2017·金华)(本题12分)如图1,在平面直角坐标系中,四边形OABC各顶点的坐标分别O(0,0),A(3, ),B(9,5 ),C(14,0).动点P与Q同时从O点出发,运动时间为t秒,点P沿OC方向以1单位长度/秒的速度向点C运动,点Q沿折线OA−AB−BC运动,在OA,AB,BC上运动的速度分别为3, , (单位长度/秒)﹒当P,Q中的一点到达C点时,两点同时停止运动. (1)求AB所在直线的函数表达式. (2)如图2,当点Q在AB上运动时,求△CPQ的面积S关于t的函数表达式及S的最大值. (3)在P,Q的运动过程中,若线段PQ的垂直平分线经过四边形OABC的顶点,求相应的t值. 25、(2017·金华)(本题10分) 如图1,将△ABC纸片沿中位线EH折叠,使点A的对称点D落在BC边上,再将纸片分别沿等腰△BED和等腰△DHC的底边上的高线EF,HG折叠,折叠后的三个三角形拼合形成一个矩形.类似地,对多边形进行折叠,若翻折后的图形恰能拼合成一个无缝隙、无重叠的矩 形,这样的矩形称为叠合矩形. (1)将□ABCD纸片按图2的方式折叠成一个叠合矩形AEFG,则操作形成的折痕分别是线段________,________;S矩形AEFG:S□ABCD=________ (2)ABCD纸片还可以按图3的方式折叠成一个叠合矩形EFGH,若EF=5,EH=12,求AD的长. (3)如图4,四边形ABCD纸片满足AD∥BC,AD查看更多