中考数学试题分类汇编及解析函数

中考数学试题分类汇编及解析函数

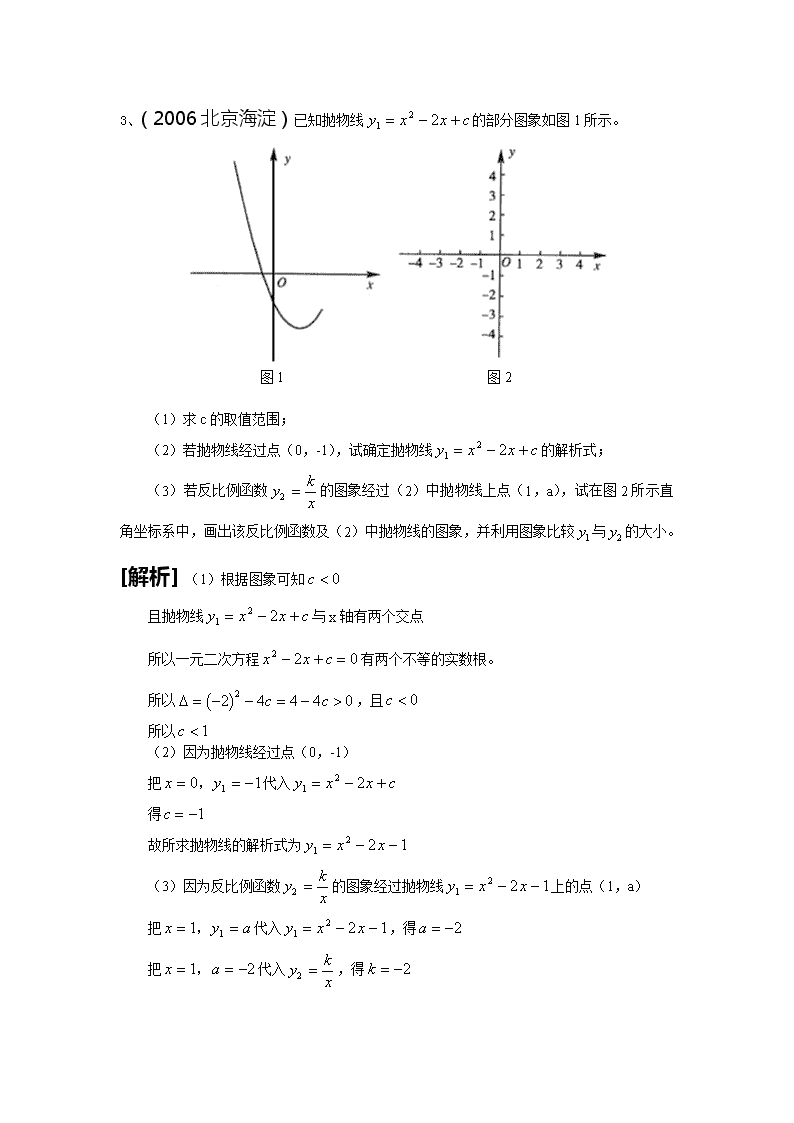
‎2006年中考数学试题分类汇编及解析-----函数 ‎1、（2006重庆）已知：是方程的两个实数根，且，抛物线的图像经过点A()、B().‎ (1) 求这个抛物线的解析式；‎ (2) 设（1）中抛物线与轴的另一交点为C,抛物线的顶点为D，试求出点C、D的坐标和△BCD的面积；（注：抛物线的顶点坐标为）‎ (3) P是线段OC上的一点，过点P作PH⊥轴，与抛物线交于H点，若直线BC把△PCH分成面积之比为2：3的两部分，请求出P点的坐标.‎ ‎[解析] （1）解方程得 由，有 所以点A、B的坐标分别为A（1，0）,B（0，5）.‎ 将A（1，0）,B（0，5）的坐标分别代入.‎ 得解这个方程组，得 所以，抛物线的解析式为 ‎（2）由，令，得 解这个方程，得 所以C点的坐标为（-5，0）.由顶点坐标公式计算，得点D（-2，9）.‎ 过D作轴的垂线交轴于M.‎ 则 ‎，‎ 所以，.‎ ‎（3）设P点的坐标为（）‎ 因为线段BC过B、C两点，所以BC所在的值线方程为.‎ 那么，PH与直线BC的交点坐标为，‎ PH与抛物线的交点坐标为.‎ 由题意，得①，即 解这个方程，得或（舍去）‎ ‎②，即 解这个方程，得或（舍去）‎ P点的坐标为或.‎ ‎2、（2006黑龙江鸡西）某工厂用一种自动控制加工机制作一批工件，该机器运行过程分为加油过程和加工过程：加工过程中，当油箱中油量为‎10升时，机器自动停止加工进入加油过程，将油箱加满后继续加工，如此往复．已知机器需运行185分钟才能将这批工件加工完．下图是油箱中油量y(升)与机器运行时间x(分)之间的函数图象．根据图象回答下列问题：‎ ‎ (1)求在第一个加工过程中，油箱中油量y(升)与机器运行时间x(分)之间的函数关系式(不必写出自变量x的取值范围)；‎ ‎ (2)机器运行多少分钟时，第一个加工过程停止?‎ ‎ (3)加工完这批工件，机器耗油多少升?‎ ‎[解析] (1)设所求函数关系式为y=kx+b．‎ ‎ 由图象可知过(10，100)，(30，80)两点，‎ ‎ 得 ‎ 解得 ‎ ‎∴ y=-x+llO ‎ ‎ (2)当y=10时，-x+110=10，x=100‎ 机器运行100分钟时，第一个加工过程停止 ‎ (3)第一个加工过程停止后再加满油只需9分钟 ‎ 加工完这批工件，机器耗油‎166升 ‎3、（2006北京海淀）已知抛物线的部分图象如图1所示。‎ 图1 图2‎ ‎ （1）求c的取值范围；‎ ‎ （2）若抛物线经过点（0，-1），试确定抛物线的解析式；‎ ‎ （3）若反比例函数的图象经过（2）中抛物线上点（1，a），试在图2所示直角坐标系中，画出该反比例函数及（2）中抛物线的图象，并利用图象比较与的大小。‎ ‎[解析] （1）根据图象可知 ‎ 且抛物线与x轴有两个交点 ‎ 所以一元二次方程有两个不等的实数根。‎ ‎ 所以，且 ‎ 所以 ‎ （2）因为抛物线经过点（0，-1）‎ ‎ 把代入 ‎ 得 ‎ 故所求抛物线的解析式为 ‎ （3）因为反比例函数的图象经过抛物线上的点（1，a）‎ ‎ 把代入，得 ‎ 把代入，得 ‎ 所以 ‎ 画出的图象如图所示。‎ ‎ ‎ ‎ 观察图象，除交点（1，-2）外，还有两个交点大致为和 ‎ 把和分别代入和可知，‎ ‎ 和是的两个交点 ‎ 根据图象可知：当或或时，‎ ‎ 当时，‎ ‎ 当时，‎ ‎4、（2006浙江嘉兴）某旅游胜地欲开发一座景观山．从山的侧面进行堪测，迎面山坡线ABC由同一平面内的两段抛物线组成，其中AB所在的抛物线以A为顶点、开口向下，BC所在的抛物线以C为顶点、开口向上．以过山脚（点C）的水平线为x轴、过山顶（点A）的铅垂线为y轴建立平面直角坐标系如图（单位：百米）．已知AB所在抛物线的解析式为，BC所在抛物线的解析式为，且已知．‎ ‎（1）设是山坡线AB上任意一点，用y表示x，并求点B的坐标；‎ ‎（2）从山顶开始、沿迎面山坡往山下铺设观景台阶．这种台阶每级的高度为‎20厘米，长度因坡度的大小而定，但不得小于‎20厘米，每级台阶的两端点在坡面上（见图）．‎ ‎①分别求出前三级台阶的长度（精确到厘米）；‎ ‎②这种台阶不能一直铺到山脚，为什么？‎ 上山方向 长度 高度 ‎（3）在山坡上的‎700米高度（点D）处恰好有一小块平地，可以用来建造索道站．索道的起点选择在山脚水平线上的点E处，（米）．假设索道DE可近似地看成一段以E为顶点、开口向上的抛物线，解析式为．试求索道的最大悬空高度．‎ ‎[解析] （1）∵是山坡线AB上任意一点，‎ ‎∴，， ‎ ‎∴， ‎ ‎∵，∴＝4，∴ ‎ ‎（2）在山坡线AB上，，‎ ‎①令，得 ；令，得 ‎∴第一级台阶的长度为（百米）（厘米） ‎ 同理，令、，可得、‎ ‎∴第二级台阶的长度为（百米）（厘米） ‎ 第三级台阶的长度为（百米）（厘米） ‎ ‎②取点，又取，则 ‎∵‎ ‎∴这种台阶不能从山顶一直铺到点B，从而就不能一直铺到山脚 ‎ ‎（注：事实上这种台阶从山顶开始最多只能铺到‎700米高度，共500级．从‎100米高度到‎700米高度都不能铺设这种台阶．解题时取点具有开放性）‎ ‎②另解：连接任意一段台阶的两端点P、Q，如图 ‎∵这种台阶的长度不小于它的高度 ‎∴‎ 当其中有一级台阶的长大于它的高时，‎ ‎ ‎ 在题设图中，作于H 则，又第一级台阶的长大于它的高 ‎∴这种台阶不能从山顶一直铺到点B，从而就不能一直铺到山脚 ‎ 上山方向 ‎（3）‎ ‎、、、‎ 由图可知，只有当索道在BC上方时，索道的悬空高度才有可能取最大值 索道在BC上方时，悬空高度 ‎ ‎ 当时，‎ ‎∴索道的最大悬空高度为米． ‎ ‎5、如图14，抛物线E：交x轴于A、B两点，‎ 交y轴于M点。抛物线E关于y轴对称的抛物线F交x轴于 C、D两点。‎ ‎⑴求F的解析式；‎ ‎⑵在x轴上方的抛物线F或E上是否存在一点N，使以A、C N、M为顶点的四边形是平行四边形。若存在，求点N坐标；‎ 若不存在，请说明理由；‎ ‎⑶若将抛物线E的解析式改为，试探索问题⑵。‎ ‎[解析] 当y=0时，，解得x1=－3，x2=－1，‎ ‎∴A、B点坐标分别为（－3，0）、（－1，0）‎ 当x＝0时，y＝3，∴M点坐标为（0，3），A、B、M三点关于y轴得对称点分别是D、C、M，∴D、C坐标为（3，0）、（1，0）‎ 设F的解析式为 ‎∴a＝1，b＝－4‎ ‎∴F的解析式为 ‎（2）存在。假设MN∥AC，∴N点的纵坐标为3。‎ 若在抛物线F上，当y=3时，，则x1=0，x2=4‎ ‎∴N点坐标为(4，3)，∴MN=4，‎ 由(1)可求AC=4，∴MN=AC，∴四边形ACNM为平行四边形。‎ 根据抛物线F和E关于y轴对称，故N点坐标为(4，3)或(－4，3)‎ ‎(3) 存在。假设MN∥AC，∴N点的纵坐标为c。设y＝0，∴‎ ‎∴，‎ ‎∴A点坐标为(，0)，B点坐标为(，0)‎ ‎∴C点坐标为(，0)，∴AC=‎ 在抛物线E上，当y=c时，，x1=0，x2=‎ ‎∴N点坐标为(，0)‎ NM=0－()=，∴NM=AC，∴四边形ACMN为平行四边形。‎ 根据抛物线F和E关于y轴对称，故N点坐标为(，c)或(，c)。‎ ‎6、（2006山东烟台）如图，已知抛物线L1: y=x2-4的图像与x有交于A、C两点 ‎（1）若抛物线l2与l1关于x轴对称，求l2的解析式；‎ ‎（2）若点B是抛物线l1上的一动点（B不与A、C重合），以AC为对角线，A、B、C三点为顶点的平行四边形的第四个顶点定为D，求证：点D在l2上；‎ ‎（3）探索：当点B分别位于l1在x轴上、下两部分的图像上时，平行四边形ABCD的面积是否存在最大值和最小值？若存在，判断它是何种特殊平行四边形，并求出它的面积；若不存在，请说明理由。‎ ‎[解析] （1）设l2的解析式为y=a(x-h)2+k ‎∵l2与x轴的交点A(-2,0),C(2,0),顶点坐标是(0，-4),l1与l2关于x轴对称，‎ ‎∴l2过A(-2,0),C(2,0),顶点坐标是（0，4）‎ ‎∴y=ax2+4‎ ‎ ∴0=‎4a+4 得 a=-1‎ ‎∴l2的解析式为y=-x2+4‎ ‎(2)设B(x1 ,y1)‎ ‎ ∵点B在l1上 ‎ ∴B(x1 ,x12-4) ‎ ‎ ∵四边形ABCD是平行四边形，A、C关于O对称 ‎ ∴B、D关于O对称 ‎ ∴D(-x1 ,-x12+4).‎ ‎ 将D(-x1 ,-x12+4)的坐标代入l2：y=-x2+4‎ ‎ ∴左边=右边 ‎ ∴点D在l2上.‎ ‎(3)设平行四边形ABCD的面积为S,则 ‎ S=2*S△ABC =AC*|y1|=4|y1|‎ ‎ a.当点B在x轴上方时，y1＞0‎ ‎ ∴S=4y1 ,它是关于y1的正比例函数且S随y1的增大而增大，‎ ‎ ∴S既无最大值也无最小值 ‎ b.当点B在x轴下方时，-4≤y1＜0‎ ‎ ∴S=-4y1 ,它是关于y1的正比例函数且S随y1的增大而减小，‎ ‎ ∴当y1 =-4时，S由最大值16，但他没有最小值 ‎ 此时B(0,-4)在y轴上，它的对称点D也在y轴上. ‎ ‎ ∴AC⊥BD ‎ ∴平行四边形ABCD是菱形 ‎ 此时S最大=16.‎ ‎7、（2006吉林长春）某厂生产一种零件，每个成本为40元，销售单价为60元。该厂为了鼓励客户购买，决定当一次购买零件超过100个时，多购买一个，全部零件的销售单价均降低0.02元，但不能低于51元。‎ ‎（1）当一次购买多少个零件时，销售单价恰为51元？ ‎ ‎（2）设一次购买零件x个时，销售单价为y元，求y与x的函数关系式。‎ ‎（3）当客户一次购买500个零件时，该厂获得的利润是多少？当客户一次购买1000个零碎件时，利润又是多少？（利润 = 售价－成本）‎ ‎[解析]‎ ‎（1）设当一次购买x个零件时，销售单价为51元，则 ‎（x－100）×0.02 = 60－51，‎ 解得 x = 550。‎ 答：当一次购买550个零件时，销售单价为51元。 ‎ ‎（2）当0＜x≤100时， y = 60；‎ 当100＜x≤550时， y = 62－0.02x；‎ 当x＞550时， y = 51。 ‎ ‎（3）当x = 500时，利润为 ‎（62－0.02×500）×500－40×500 = 6000（元）。‎ 当x = 1000时，利润为1000×（51－40）= 11000（元）。‎ 答：当一次购买500个零件时，该厂获得利润为6000元；当一次购买1000个零件时，该厂获得利润11000元。 ‎ ‎8、（2006吉林长春）如图，在平面直角坐标系中，两个函数的图象交于点A。动点P从点O开始沿OA方向以每秒1个单位的速度运动，作PQ∥x轴交直线BC于点Q，以PQ为一边向下作正方形PQMN，设它与△OAB重叠部分的面积为S。‎ ‎（1）求点A的坐标。‎ ‎（2）试求出点P在线段OA上运动时，S与运动时间t（秒）的关系式。‎ ‎（3）在（2）的条件下，S是否有最大值？若有，求出t为何值时，S有最大值，并求出最大值；若没有，请说明理由。‎ ‎（4）若点P经过点A后继续按原方向、原速度运动，当正方形PQMN与△OAB重叠部分面积最大时，运动时间t满足的条件是____________。‎ ‎[解析]‎ ‎（1）由 可得 ‎ ∴A（4，4）。 ‎ ‎（2）点P在y = x上，OP = t，‎ 则点P坐标为 点Q的纵坐标为，并且点Q在上。‎ ‎∴，‎ 即点Q坐标为。‎ ‎。 ‎ 当时，。‎ 当，‎ ‎ ‎ 当点P到达A点时，，‎ 当时，‎ ‎ ‎ ‎ 。‎ ‎（3）有最大值，最大值应在中，‎ 当时，S的最大值为12。 ‎ ‎（4）。 ‎ ‎9、（2006临安）如图，△OAB是边长为的等边三角形，其中O是坐标原点，顶点B在轴正方向上，将△OAB 折叠，使点A落在边OB上，记为A′，折痕为EF.‎ ‎（1）当A′E//轴时，求点A′和E的坐标；‎ ‎（2）当A′E//轴，且抛物线经过点A′和E时，求抛物线与轴的交点的坐标；‎ （3） 当点A′在OB上运动，但不与点O、B重合时，能否使△A′EF成为直角三角形？若能，请求出此时点A′的坐标；若不能，请你说明理由.‎ ‎[解析]（1）由已知可得∠A，OE=60o , A，E=AE 由A′E//轴,得△OA，E是直角三角形，‎ 设A，的坐标为（0，b）‎ AE=A，E=,OE=2b 所以b=1，A，、E的坐标分别是（0，1）与（，1） ‎ （2） 因为A，、E在抛物线上，所以 所以，函数关系式为 由得 与x轴的两个交点坐标分别是（，0）与（，0）‎ （2） 不可能使△A′EF成为直角三角形。‎ ‎∵∠FA，E=∠FAE=60o,若△A′EF成为直角三角形,只能是∠A，EF=90o或∠A，FE=90o 若∠A，EF=90o,利用对称性,则∠AEF=90o, A，、E、A三点共线，O与A重合，与已知矛盾；‎ 同理若∠A，FE=90o也不可能 所以不能使△A′EF成为直角三角形。 ‎