- 2021-05-10 发布 |
- 37.5 KB |
- 96页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
中考数学试题分类全集04 101一次函数
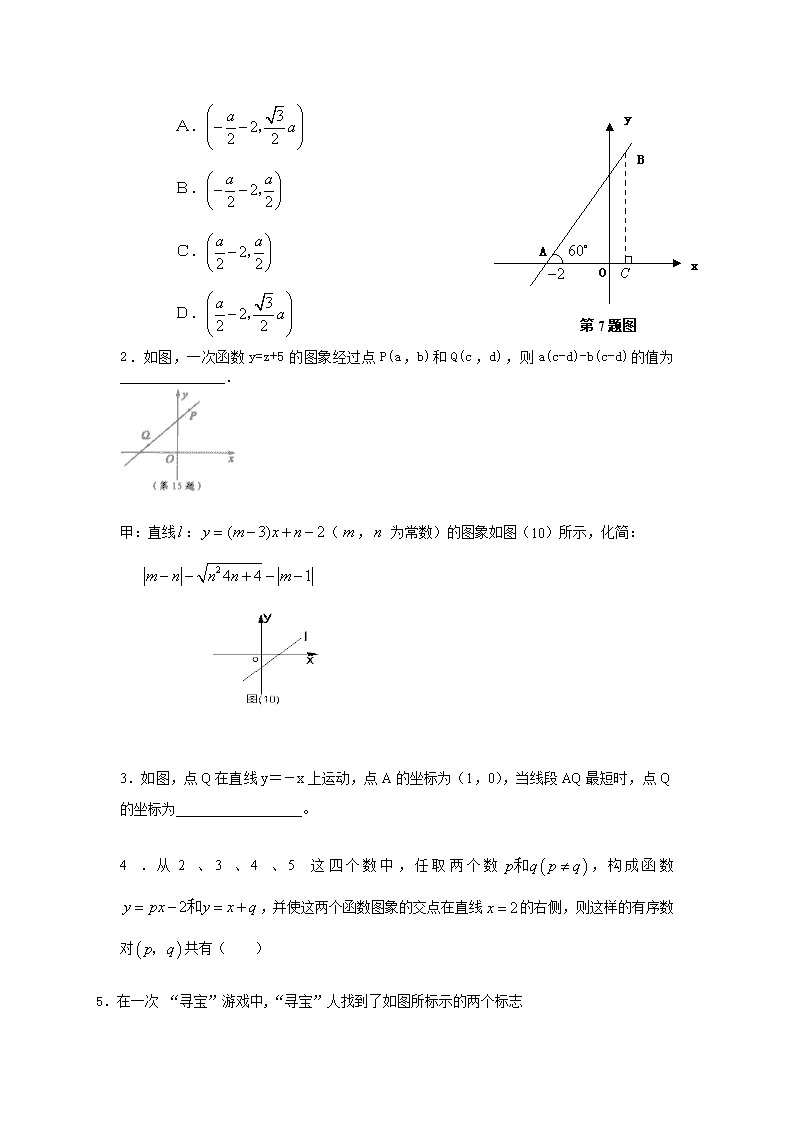
(一) 1.直线l1:y=k1x+b与直线l2:y=k2x+c在同一平面直角坐标系中的图象如图所示,则关于x的不等式k1x+b<k2x+c的解集为( ). A、x>1 B、x<1 C、x>-2 D、x<-2 O 1 x y (第05题图) -2 y=k2x+c y=k1x+b 2.(2010四川乐山)已知一次函数y=kx+b,当0≤x≤2时,对应的函数值y的取值范围是-2≤y≤4,则kb的值为( ) A. 12 B. -6 C. -6或-12 D. 6或1 3.已知整数x满足-5≤x≤5,y1=x+1,y2=-2x+4,对任意一个x,m都取y1,y2中的较小值,则m的最大值是 A.1 B.2 C.24 D.-9 4.已知直线,,的图象如图所示,若无论取何值,总取、、中的最小值,则的最大值为 。 5.已知a、b、c为非零实数,且满足 = = = k ,则一次函数y= kx+(1+k)的图象一定经过 ( ) A. 第一、二、三象限 B.第二、四象限 C. 第一象限 D.第二象限 (二) 1.如图,平面直角坐标系中,直线与轴的夹角为,且点的坐标为,点在轴的上方,设,那么点的坐标为 C O B x y A 第7题图 A. B. C. D. 2.如图,一次函数y=z+5的图象经过点P(a,b)和Q(c,d),则a(c-d)-b(c-d)的值为_______________. 甲:直线:(, 为常数)的图象如图(10)所示,化简: 3.如图,点Q在直线y=-x上运动,点A的坐标为(1,0),当线段AQ最短时,点Q的坐标为__________________。 4.从2、3、4、5这四个数中,任取两个数,构成函数,并使这两个函数图象的交点在直线的右侧,则这样的有序数对共有( ) 5.在一次 “寻宝”游戏中,“寻宝”人找到了如图所标示的两个标志 点A、B,A、B两点到“宝藏”点的距离都是,则 “宝藏”点的坐标是 (10题图) A. B. C.或 D.或 6.如图,点A、B、C、D在一次函数的图象上,它们的横坐标依次为-1、1、2,分别过这些点作x轴与y轴的垂线,则图中阴影部分的面积这和是 ( ) A. B. C. D. 12.在平面直角坐标系中,A点的坐标为,C点的坐标为。 (1)如图1,若直线AB∥OC,点D是线段OC的中点,点P在射线AB上运动,当△OPD是腰长为5的等腰三角形时,直接写出点P的坐标; (2)如图2,若直线AB与OC不平行,AB所在直线上是否存在点P,使△OPC是直角三角形,且∠OPC=90º,若有这样的点P,求出它的坐标,若没有,请简要说明理由。 12、①解:(3,4) (2,4) (8,4) …………………(每个点2分) ②设点P的坐标为(a,-a+4),过点P作PH⊥OC于点H ∵ ∠OPC=90° ∴△OPH∽△PCH ∴ 即=OH.CH……(2分) ∴ ∴ ……(2分) ∴(1,3) (8,-4) …(1分) 25.(本题满分10分) Q P (1)∵, ∴,. ∴,.…………………1分 点,点分别在轴,轴的正半轴上, ∴A(1,0),B(0,). ……………2分 (2)由(1),得AC=4,,. ∴. ∴△ABC为直角三角形,. …………………………………………4分 设CP=t,过P作PQ⊥CA于Q,由△CPQ∽△CBO,易得PQ=. ∴S= ==-t(0≤t<). …………………………7分 (说明:不写t的范围不扣分) (3)存在,满足条件的的有两个. , ………………………………………………………………………8分 .…………………………………………………………………10分 28.(本小题满分10分) 如图,在平面直角坐标系中,点,点分别在轴,轴的正半轴上,且满足. (1)求点,点的坐标. (2)若点从点出发,以每秒1个单位的速度沿射线运动,连结.设的面积为,点的运动时间为秒,求与的函数关系式,并写出自变量的取值范围. (3)在(2)的条件下,是否存在点,使以点为顶点的三角形与 相似?若存在,请直接写出点的坐标;若不存在,请说明理由. 28.解:(1) , (1分) , 点,点分别在轴,轴的正半轴上 (2分) (2)求得 (3分) (每个解析式各1分,两个取值范围共1分) (6分) (3);;;(每个1分,计4分) (10分) 注:本卷中所有题目,若由其它方法得出正确结论,酌情给分. 16.如图, 在已建立直角坐标系的4×4正方形方格纸中,△是格点 三角形(三角形的三个顶点都是小正方形的顶点), 若以格点、 、为顶点的三角形与△相似(全等除外),则格点的坐标 是 ▲ . O 1 1 2 3 2 3 4 4 (第16题) 图7 图8 19. 图7中外接圆的圆心坐标是 . 图7 图8 19. 图7中外接圆的圆心坐标是 . 26.(12分)如图,已知一次函数的图象与轴,轴分别相交于两点,点在上以每秒1个单位的速度从点向点运动,同时点在线段上以同样的速度从点向点运动,运动时间用(单位:秒)表示. (1)求的长; (2)当为何值时,与相似?并直接写出此时点的坐标; (3)的面积是否有最大值?若有,此时为何值?若没有,请说明理由. 图5 18.如图5,在平面直角坐标系中,点P是第一象限直线上的点,点A,O是坐标原点,△PAO的面积为 ⑴求与的函数关系式 ⑵当时,求的值 26.(12分)如图,已知一次函数的图象与轴,轴分别相交于两点,点在上以每秒1个单位的速度从点向点运动,同时点在线段上以同样的速度从点向点运动,运动时间用(单位:秒)表示. (1)求的长; (2)当为何值时,与相似?并直接写出此时点的坐标; (3)的面积是否有最大值?若有,此时为何值?若没有,请说明理由. O A B C P x y (第25题图) 25.(12分)如图,A、B分别为x轴和y轴正半轴上的点。OA、OB的长分别是方程x2-14x+48=0的两根(OA>OB),直线BC平分∠ABO交x轴于C点,P为BC上一动点,P点以每秒1个单位的速度从B点开始沿BC方向移动。 (1)设△APB和△OPB的面积分别为S1、S2,求S1∶S2的值; (2)求直线BC的解析式; (3)设PA-PO=m,P点的移动时间为t。 ①当0<t≤时,试求出m的取值范围; ②当t>时,你认为m的取值范围如何(只要求写出结论)? 24.如图,已知A(8,0),B(0,6),两个动点P、Q同时在△OAB 的边上按逆时针方向(→O→A→B→O→)运动,开始时点P在点B位置,点Q在点O位置,点P的运动速度为每秒2个单位,点Q的运动速度为每秒1个单位. (1)在前3秒内,求△OPQ的最大面积; (2)在前10秒内,求P、Q两点之间的最小距离,并求此时点P、Q的坐标; (3)在前15秒内,探究PQ平行于△OAB一边的情况,并求平行时点P、Q的坐标. 24.(1)∵,,∴,,. 在前3秒内,点P在OB上、点Q在OA上, 设经过t秒,点P、Q位置如图. 则,. ∴△OPQ 的面积,(2分) 当时,. (2分) (2)在前10秒内,点P从B开始,经过点O、点A,最后到达AB上,经过的总路程为20;点Q从O开始,经过点A,最后也到达AB上,经过的总路程为10.其中P、Q两点在某一位置重合,最小距离为0. 设经过t秒,点Q被点P“追及”(两点重合),则,∴. ∴在前10秒内,P、Q两点的最小距离为0,点P、Q的相应坐标为.(4分) (3)①设,则点P在OB上、点Q在OA上, ,. 若,则, ∴,解得. 此时,,.(2分) ②设,则点P、Q都在OA上,不存在PQ平行于△OAB一边的情况. ③设,则点P在AB上、点Q在OA上, ,. 若,则, ∴,解得. 此时,,.(2分) ④设,则点P、Q都在AB上,不存在PQ平行于△OAB一边的情况. ⑤设,则点P在OB上、点Q在AB上, ,. 若,则, ∴,解得. 此时,,.(2分) 26、如图,在平面直角坐标系中,两个函数的图象交于点A。动点P从点O开始沿OA方向以每秒1个单位的速度运动,作PQ∥x轴交直线BC于点Q,以PQ为一边向下作正方形PQMN,设它与△OAB重叠部分的面积为S。 (1)求点A的坐标。(2分) (2)试求出点P在线段OA上运动时,S与运动时间t(秒)的关系式。(4分) (3)在(2)的条件下,S是否有最大值?若有,求出t为何值时,S有最大值,并求出最大值;若没有,请说明理由。(2分) (4分)若点P经过点A后继续按原方向、原速度运动,当正方形PQMN与△OAB重叠部分面积最大时,运动时间t满足的条件是____________。(2分) 26、(1)由 可得 ∴A(4,4)。 (2分) (2)点P在y = x上,OP = t, 则点P坐标为 点Q的纵坐标为,并且点Q在上。 ∴, 即点Q坐标为。 。 (4分) 当时,。 当, (5分) 当点P到达A点时,, 当时, (6分) 。 (3)有最大值,最大值应在中, 当时,S的最大值为12。 (8分) (4)。 (10分) y=- x+2 图12 y=x O x y 25.如图12,P是y轴上一动点,是否 存在平行于y轴的直线x=t,使它与直线 y=x和直线分别交于点D、E (E在D的上方),且△PDE为等腰直角三 角形。若存在,求t的值及点P的坐标; 若不存在,请说明原因。 25.解:存在。 方法一:当x=t时,y=x=t、当x=t时,。 ∴E点的坐标为(t,),D点坐标为(t,t)。……………………2分 ∵E在D的上方,∴,且t<。……………3分 ∵△PDE为等腰直角三角形,∴PE=DE或PD=DE或PE=PD。………………4分 若t>0,PE=DE时,。 ∴。∴P点坐标为(0,)。………………………………5分 若t>0,PD=DE时,, ∴。∴P点坐标为(0,)。………………………………………………6分 若t>0,PE=PD时,即DE为斜边,∴。………………………7分 ∴,∴DE的中点的坐标为(t,), ∴P点坐标为(0,)。………………………………………………………8分 若t<0,PE=PD时,由已知得DE=-t,, t=4>0(不符合题意,舍去),此时直线x=t不存在。………………………10分 若t<0,PE=PD时,即DE为斜边时,由已知得DE=-2t, ,…………………………………………………………………11分 ∴。∴P点坐标为(0,0)…………………………………12分 综上所述:当t=时,△PDE为等腰直角三角形,此时P点坐标为(0,)或 (0,);当时,△PDE为等腰直角三角形,此时P点坐标为(0,);当t=-4时,△PDE为等腰直角三角形,此时P点坐标为(0,0)。 方法二:设直线交y轴于点A,交直线y=x于点B,过B做BM垂直于y轴,垂足为M,交DE于点N。∵x=t平行于y轴,∴MN=。…1分 ∵ 解得 ∴B点坐标为(,), ∴BM=…………………………………………………………………………2分 当x=0时,,∴A点坐标为(0,2),∴OA=2。…………3分 ∵△PDE为等腰直角三角形,∴PE=DE或PD=DE或PE=PD。………………4分 y=- x+2 图4 y=x O x y N D E M A B 如图4,若t>0,PE=DE和PD=DE时,∴PE=t,PD=t,∵DE∥OA, ∴△BDE∽△BOA,∴………5分 ∴ ∴t=。 当t=时,。 ∴P点坐标为(0,)或(0,)。…6分 若t>0,PD=PE时,即DE为斜边,∴DE=2MN=2t。 M B A y=- x+2 图5 y=x O x y N D E ∵DE∥OA,∴△BDE∽△BOA∴…7分 ∴,∴MN=t=, DE的中点的纵坐标为。 ∴P点的坐标为(0,)………………8分 如图5,若t<0,PE=DE或PD=DE时, ∵DE∥OA, ∴△BDE∽△BOA∴…………9分 DE=-4(不符合题意,舍去),此时直线x=t不存在。…………………10分 若t<0,PE=PD时,即DE为斜边,∴DE=2MN=-2t。 ∵DE∥OA,∴△BDE∽△BOA∴……………………………11分 ∴,∴MN=4,∴t=-4,。 ∴P点坐标为(0,0)…………………………………………………………12分 综上所述:当t=时,△PDE为等腰直角三角形,此时P点坐标为(0,)或 (0,);当时,△PDE为等腰直角三角形,此时P点坐标为(0,);当t=-4时,△PDE为等腰直角三角形,此时P点坐标为(0,0)。 26.(本题满分12分) 如图,已知直线的函数表达式为,且与轴,轴分别交于两点,动点从点开始在线段上以每秒2个单位长度的速度向点移动,同时动点从点开始在线段上以每秒1个单位长度的速度向点移动,设点移动的时间为秒. (1)求出点的坐标; (2)当为何值时,与相似? O P A Q B y x (3)求出(2)中当与相似时,线段所在直线的函数表达式. 26.解:(1)由, 令,得; 令,得. 1分 的坐标分别是. 2分 (2)由,,得. 当移动的时间为时,,. 3分 ,当时 , 4分 (秒). 5分 ,当时, , . 6分 (秒). 7分 秒或秒,经检验,它们都符合题意,此时与相似. 8分 (3)当秒时,, , ,,. 9分 线段所在直线的函数表达式为. 10分 当时,,,,. 设点的坐标为,则有, . 当时,, 的坐标为. 11分 设的表达式为, 则,,的表达式为. 12分 24.(本题14分) 如图,平面直角坐标系中,直线AB与轴,轴分别交于A(3,0),B(0,)两点, ,点C为线段AB上的一动点,过点C作CD⊥轴于点D. (1)求直线AB的解析式; (2)若S梯形OBCD=,求点C的坐标; (3)在第一象限内是否存在点P,使得以P,O,B为顶点的 三角形与△OBA相似.若存在,请求出所有符合条件 的点P的坐标;若不存在,请说明理由. 24.(本题14分) (1)直线AB解析式为:y=x+. ……………(3分) (2)方法一:设点C坐标为(x,x+),那么OD=x,CD=x+. ∴==. ………(2分) 由题意: =,解得(舍去) ………(2分) ∴ C(2,) ………(1分) 方法二:∵ ,=,∴.…(2分) 由OA=OB,得∠BAO=30°,AD=CD. ∴ =CD×AD==.可得CD=. ………(2分) ∴ AD=1,OD=2.∴C(2,). ………(1分) (3)当∠OBP=Rt∠时,如图 ①若△BOP∽△OBA,则∠BOP=∠BAO=30°,BP=OB=3, ∴(3,). ……(2分) ②若△BPO∽△OBA,则∠BPO=∠BAO=30°,OP=OB=1. ∴(1,). …………(1分) 当∠OPB=Rt∠时 ③ 过点P作OP⊥BC于点P(如图),此时△PBO∽△OBA,∠BOP=∠BAO=30° 过点P作PM⊥OA于点M. 方法一: 在Rt△PBO中,BP=OB=,OP=BP=. ∵ 在Rt△PMO中,∠OPM=30°, ∴ OM=OP=;PM=OM=.∴(,). ……(1分) 方法二:设P(x ,x+),得OM=x ,PM=x+ 由∠BOP=∠BAO,得∠POM=∠ABO. ∵tan∠POM=== ,tan∠ABOC==. ∴x+=x,解得x=.此时,(,). ……(1分) ④若△POB∽△OBA(如图),则∠OBP=∠BAO=30°,∠POM=30°. ∴ PM=OM=. ∴ (,)(由对称性也可得到点的坐标).…………(2分) 当∠OPB=Rt∠时,点P在x轴上,不符合要求. 综合得,符合条件的点有四个,分别是: (3,),(1,),(,),(,). 注:四个点中,求得一个P点坐标给2分,两个给3分,三个给4分,四个给6分. 26.(12分)如图,已知一次函数的图象与轴,轴分别相交于两点,点在上以每秒1个单位的速度从点向点运动,同时点在线段上以同样的速度从点向点运动,运动时间用(单位:秒)表示. (1)求的长; (2)当为何值时,与相似?并直接写出此时点的坐标; (3)的面积是否有最大值?若有,此时为何值?若没有,请说明理由. 24、(14分)如图,一次函数y=ax+b的图象与反比例函数y=k/x的图象交于A、B、两点,与x轴交于点C,与y轴交于点D,已知OA= ,tan∠AOC=1/3,点B的坐标为(m,-2)。 (1)求反比例函数的解析式 (2)求一次函数的解析式 (3)在y轴上存在一点P,是的△PDC与△ODC相似, 请你求出P点的坐标。 y x A C O D B 24.(10分)如图,一次函数y=ax+b的图象与反比例函数y= 的图象交于A、B两点,与x轴交于点C,与y轴交于点D, 已知OA=,点B的坐标为(m,-2),tan∠AOC=. (1)求反比例函数的解析式; (2)求一次函数的解析式; (3)在y轴上存在一点P,使△PDC与△CDO相似,求P点的坐标. 24.(本题满分10分) (1)过点作⊥轴,垂足为. y x A C O D B P E 点的坐标为(3,1).………………………2分 点在双曲线上,,. 双曲线的解析式 为. ………………………………………………………3分 (2)点在双曲线上, . 点的坐标 为. ………………………………………………………4分 一次函数的解析式 为. …………………………………………………7分 (3)两点在直线上,的坐标分别是. ,. ………………………………………8分 过点作,垂足为点. , 又, 点坐标为. ……………………………………………………10分 y x P B D A O C 22.如图,一次函数的图象与反比例函数的 图象交于点P,点P在第一象限.PA⊥x轴于点A,PB⊥y 轴于点B.一次函数的图象分别交轴、轴于点C、D, 且S△PBD=4,. (1)求点D的坐标; (2)求一次函数与反比例函数的解析式; (3)根据图象写出当时,一次函数的值大于反比例 函数的值的的取值范围. 22.解:(1)在中,令得 ∴点D的坐标为(0,2)………2分 (2)∵ AP∥OD ∴Rt△PAC ∽ Rt△DOC…………………………………1分 ∵ ∴ ∴AP=6…………………………2分 又∵BD= ∴由S△PBD=4可得BP=2…………………………3分 ∴P(2,6) …………4分 把P(2,6)分别代入与可得 一次函数解析式为:y=2x+2…………………………………………………5分 反比例函数解析式为:……………………………………………… 27.(本小题满分10分) 如图,将一块直角三角形纸板的直角顶点放在处,两直角边分别与轴平行, 纸板的另两个顶点恰好是直线与双曲线的交点. (1)求和的值; (2)设双曲线在之间的部分为,让一把三角尺的直角顶点在上 滑y x O N M C A B P (第27题图) 动,两直角边始终与坐标轴平行,且与线段交于两点,请探究是否存在点使得,写出你的探究过程和结论. 23.(8分)如图,反比例函数y=(x>0)的图象与一次函数y=-x+的图象交于A、B两点,点C的坐标为(1,),连接AC,AC∥y轴. (1)求反比例函数的解析式及点B的坐标; (2)现有一个直角三角板,让它的直角顶点P在反比例函数图象上A、B之间的部分滑动(不与A、B重合),两直角边始终分别平行于x轴、y轴,且与线段AB交于M、N两点,试判断P点在滑动过程中△PMN是否与△CBA总相似?简要说明判断理由. 23.(1)由得,代入反比例函数中,得 ∴反比例函数解析式为: 2分 解方程组由化简得: 所以 5分 (2)无论点在之间怎样滑动,与总能相似.因为两点纵坐标相等,所以轴. 又因为轴,所以为直角三角形. 同时也是直角三角形, 8分 (在理由中只要能说出轴,即可得分.) 24.(本题满分10分) 如图,已知反比例函数的图象与一次函数的图象交于、两点,. (1)求反比例函数和一次函数的关系式; 第24题 (2)在直线上是否存在一点,使∽,若存在,求点坐标;若不存在,请说明理由. x y A B O D C (第19题) 19.如图,一次函数的图象与反比例函数的图象交于两点,直线分别交轴、轴于两点. (1)求上述反比例函数和一次函数的解析式; (2)求的值. 19.解:(1)把,代入,得:. 反比例函数的解析式为. 把,代入得. x y A B O E D C (第19题) 把,;,分别代入 得, 解得, 一次函数的解析式为. (2)过点作轴于点. 点的纵坐标为1,. 由一次函数的解析式为得点的坐标为, . 在和中,,, . . 22.已知:等腰三角形OAB在直角坐标系中的位置如图,点A的坐标为(),点B的坐标为(-6,0). (1)若三角形OAB关于y轴的轴对称图形是三角形O, 请直接写出A、B的对称点的坐标; (2)若将三角形沿x轴向右平移a个单位,此时点A 恰好落在反比例函数的图像上,求a的值; (3)若三角形绕点O按逆时针方向旋转度(). ①当=时点B恰好落在反比例函数的图像上,求k的值. ②问点A、B能否同时落在①中的反比例函数的图像上,若能,求出 的值;若不能,请说明理由. 22.解:(1) ………(每个点坐标写对各得2分)………………………4分 (2) ∵ ∴…1分 ∴ …………………1分 ∴ …………………2分 (3) ① ∵ ∴相应B点的坐标是 …………………………………………………1分 ∴. …………………………………………………………………………1分 ② 能 ………………………………………………………………………………1分 当时,相应,点的坐标分别是, 经经验:它们都在的图像上 ∴ ………………………………………………………………………1分 E D B A x y O C 22.如图,已知正比例函数y = ax(a≠0)的图象与反比例函致(k≠0)的图象的一个交点为A(-1,2-k2),另—个交点为B,且A、B关于原点O对称,D为OB的中点,过点D的线段OB的垂直平分线与x轴、y轴分别交于C、E. (1)写出反比例函数和正比例函数的解析式; (2)试计算△COE的面积是△ODE面积的多少倍. 22.(1)由图知k>0,a>0.∵ 点A(-1,2-k2)在图象上, ∴ 2-k2 =-k,即 k2-k-2 = 0,解得 k = 2(k =-1舍去),得反比例函数为. 此时A(-1,-2),代人y = ax,解得a = 2,∴ 正比例函数为y = 2x. (2)过点B作BF⊥x轴于F.∵ A(-1,-2)与B关于原点对称, ∴ B(1,2),即OF = 1,BF = 2,得 OB =. 由图,易知 Rt△OBF∽Rt△OCD,∴ OB : OC = OF : OD,而OD = OB∕2 =∕2, ∴ OC = OB · OD∕OF = 2.5.由 Rt△COE∽Rt△ODE得 , 所以△COE的面积是△ODE面积的5倍. 24、(14分)如图,一次函数y=ax+b的图象与反比例函数y=k/x的图象交于A、B、两点,与x轴交于点C,与y轴交于点D,已知OA= ,tan∠AOC=1/3,点B的坐标为(m,-2)。 (1)求反比例函数的解析式 (2)求一次函数的解析式 (3)在y轴上存在一点P,是的△PDC与△ODC相似, 请你求出P点的坐标。 y x A C O D B 24.(10分)如图,一次函数y=ax+b的图象与反比例函数y= 的图象交于A、B两点,与x轴交于点C,与y轴交于点D, 已知OA=,点B的坐标为(m,-2),tan∠AOC=. (1)求反比例函数的解析式; (2)求一次函数的解析式; (3)在y轴上存在一点P,使△PDC与△CDO相似,求P点的坐标. 24.(本题满分10分) (1)过点作⊥轴,垂足为. y x A C O D B P E 点的坐标为(3,1).………………………2分 点在双曲线上,,. 双曲线的解析式 为. ………………………………………………………3分 (2)点在双曲线上, . 点的坐标 为. ………………………………………………………4分 一次函数的解析式 为. …………………………………………………7分 (3)两点在直线上,的坐标分别是. ,. ………………………………………8分 过点作,垂足为点. , 又, 点坐标为. ……………………………………………………10分 y x P B D A O C 22.如图,一次函数的图象与反比例函数的 图象交于点P,点P在第一象限.PA⊥x轴于点A,PB⊥y 轴于点B.一次函数的图象分别交轴、轴于点C、D, 且S△PBD=4,. (1)求点D的坐标; (2)求一次函数与反比例函数的解析式; (3)根据图象写出当时,一次函数的值大于反比例 函数的值的的取值范围. 22.解:(1)在中,令得 ∴点D的坐标为(0,2)………2分 (2)∵ AP∥OD ∴Rt△PAC ∽ Rt△DOC…………………………………1分 ∵ ∴ ∴AP=6…………………………2分 又∵BD= ∴由S△PBD=4可得BP=2…………………………3分 ∴P(2,6) …………4分 把P(2,6)分别代入与可得 一次函数解析式为:y=2x+2…………………………………………………5分 反比例函数解析式为:……………………………………………… 27.(本小题满分10分) 如图,将一块直角三角形纸板的直角顶点放在处,两直角边分别与轴平行, 纸板的另两个顶点恰好是直线与双曲线的交点. (1)求和的值; (2)设双曲线在之间的部分为,让一把三角尺的直角顶点在上 滑y x O N M C A B P (第27题图) 动,两直角边始终与坐标轴平行,且与线段交于两点,请探究是否存在点使得,写出你的探究过程和结论. 23.(8分)如图,反比例函数y=(x>0)的图象与一次函数y=-x+的图象交于A、B两点,点C的坐标为(1,),连接AC,AC∥y轴. (1)求反比例函数的解析式及点B的坐标; (2)现有一个直角三角板,让它的直角顶点P在反比例函数图象上A、B之间的部分滑动(不与A、B重合),两直角边始终分别平行于x轴、y轴,且与线段AB交于M、N两点,试判断P点在滑动过程中△PMN是否与△CBA总相似?简要说明判断理由. 23.(1)由得,代入反比例函数中,得 ∴反比例函数解析式为: 2分 解方程组由化简得: 所以 5分 (2)无论点在之间怎样滑动,与总能相似.因为两点纵坐标相等,所以轴. 又因为轴,所以为直角三角形. 同时也是直角三角形, 8分 (在理由中只要能说出轴,即可得分.) 24.(本题满分10分) 如图,已知反比例函数的图象与一次函数的图象交于、两点,. (1)求反比例函数和一次函数的关系式; 第24题 (2)在直线上是否存在一点,使∽,若存在,求点坐标;若不存在,请说明理由. x y A B O D C (第19题) 19.如图,一次函数的图象与反比例函数的图象交于两点,直线分别交轴、轴于两点. (1)求上述反比例函数和一次函数的解析式; (2)求的值. 19.解:(1)把,代入,得:. 反比例函数的解析式为. 把,代入得. x y A B O E D C (第19题) 把,;,分别代入 得, 解得, 一次函数的解析式为. (2)过点作轴于点. 点的纵坐标为1,. 由一次函数的解析式为得点的坐标为, . 在和中,,, . . 22.已知:等腰三角形OAB在直角坐标系中的位置如图,点A的坐标为(),点B的坐标为(-6,0). (1)若三角形OAB关于y轴的轴对称图形是三角形O, 请直接写出A、B的对称点的坐标; (2)若将三角形沿x轴向右平移a个单位,此时点A 恰好落在反比例函数的图像上,求a的值; (3)若三角形绕点O按逆时针方向旋转度(). ①当=时点B恰好落在反比例函数的图像上,求k的值. ②问点A、B能否同时落在①中的反比例函数的图像上,若能,求出 的值;若不能,请说明理由. 22.解:(1) ………(每个点坐标写对各得2分)………………………4分 (2) ∵ ∴…1分 ∴ …………………1分 ∴ …………………2分 (3) ① ∵ ∴相应B点的坐标是 …………………………………………………1分 ∴. …………………………………………………………………………1分 ② 能 ………………………………………………………………………………1分 当时,相应,点的坐标分别是, 经经验:它们都在的图像上 ∴ ………………………………………………………………………1分 E D B A x y O C 22.如图,已知正比例函数y = ax(a≠0)的图象与反比例函致(k≠0)的图象的一个交点为A(-1,2-k2),另—个交点为B,且A、B关于原点O对称,D为OB的中点,过点D的线段OB的垂直平分线与x轴、y轴分别交于C、E. (1)写出反比例函数和正比例函数的解析式; (2)试计算△COE的面积是△ODE面积的多少倍. 22.(1)由图知k>0,a>0.∵ 点A(-1,2-k2)在图象上, ∴ 2-k2 =-k,即 k2-k-2 = 0,解得 k = 2(k =-1舍去),得反比例函数为. 此时A(-1,-2),代人y = ax,解得a = 2,∴ 正比例函数为y = 2x. (2)过点B作BF⊥x轴于F.∵ A(-1,-2)与B关于原点对称, ∴ B(1,2),即OF = 1,BF = 2,得 OB =. 由图,易知 Rt△OBF∽Rt△OCD,∴ OB : OC = OF : OD,而OD = OB∕2 =∕2, ∴ OC = OB · OD∕OF = 2.5.由 Rt△COE∽Rt△ODE得 , 所以△COE的面积是△ODE面积的5倍. (一)等腰三角形 1.一次函数y=x+4分别交x轴、y轴于A、B两点,在x轴上取一点,使△ABC为等腰三角形,则这样的的点C最多有 个. 2.在平面直角坐标系xoy中,已知点P(-2,1)关于y轴的对称点P’,点T (t,0)是x轴上的一个动点,当△P’TO是等腰三角形时,t的值是__________________。 3.如图,点A的坐标是(1,1),若点B在x轴上,且△ABO是 等腰三角形,则点B的坐标不可能是( ). 1 2 -1 y O 1 x A A.(2,0) B.(,0) C.(,0) D.(1,0) 4.在平面直角坐标系xOy中,已知点P(2,2),点Q在y轴上, △PQO是等腰三角形,则满足条件的点Q共有 A.5个 B.4个 C.3个 D.2个 O (第16题图) 6.如图,中,点的坐标为(0,1),点的坐标为(4,3),如果要使与 全等,那么点的坐标是 . 1.如图,在平面直角坐标系xoy中,分别平行x、y轴的两直 线a、b相交于点A(3,4).连接OA,若在直线a上存在点P, 使△AOP是等腰三角形.那么所有满足条件的点P的坐标是 12题图 2、(14分)一次函数过点(1,4),且分别与x轴、y轴交于A、B点,点P(a,0)在x轴正半轴上运动,点Q(0,b)在y轴正半轴上运动,且PQ⊥AB (1)求 的值,并在直角坐标系中画出一次函数的图象; (2)求a、b满足的等量关系式; (3)若△APQ是等腰三角形,求△APQ的面积。 4. (本小题满分12 分) 如图12,直线y=kx-1与x轴、y轴分别交与B、C两点,tan∠OCB=. (1) 求B点的坐标和k的值; (2) 若点A(x,y)是第一象限内的直线y=kx-1上的一个动点.当点A运动过程中,试写出△AOB的面积S与x的函数关系式; (3) 探索: ① 当点A运动到什么位置时,△AOB的面积是; ② 在①成立的情况下,x轴上是否存在一点P,使△POA是等腰三角形.若存在,请写出满足条件的所有P点的坐标;若不存在,请说明理由. 图12 (二)等边三角形 A O P C B x y 1.如图,等边△ABC的顶点A、B的坐标分别为(-,0)、 (0,1),点P(3,a)在第一象限内,且满足2S△ABP=S△ABC, 则a的值为( ) A. B. C. D.2 2.已知边长为的正三角形,两顶点分别在平面直角坐标系的轴、轴的正半轴上滑动,点C在第一象限,连结OC,则OC的长的最大值是 . O y x (A) A1 C 1 1 2 B A2 A3 B3 B2 B1 16题图 5.如图所示,已知:点,,在内依次作等边三角形,使一边在轴上,另一个顶点在边上,作出的等边三角形分别是第1个,第2个,第3个,…,则第个等边三角形的边长等于 . 1.(08河北)(本小题满分8分) l1 l2 x y D O 3 B C A (4,0) 图11 如图11,直线的解析表达式为,且与轴交于点,直线经过点,直线,交于点. (1)求点的坐标; (2)求直线的解析表达式; (3)求的面积; (4)在直线上存在异于点的另一点,使得 与的面积相等,请直接写出点的坐标. 解:(1)由,令,得... (2)设直线的解析表达式为,由图象知:,;,. 直线的解析表达式为. (3)由解得. ,. (4) 2.如图,已知一次函数的图象经过,两点,并且交x轴于点C,交y轴于点D, B D C A O 1 1 (第23题) y x (1)求该一次函数的解析式; (2)求的值; (3)求证:. 2.(1)由,解得,所以 4分 (2),. 在△OCD中,,, ∴. 8分 B D C A O 1 1 (第23题) y x E (3)取点A关于原点的对称点, 则问题转化为求证. 由勾股定理可得, ,,, ∵, ∴△EOB是等腰直角三角形. ∴. ∴. 12分 28.(本小题满分10分) 直线与坐标轴分别交于两点,动点同时从点出发,同时到达点,运动停止.点沿线段 运动,速度为每秒1个单位长度,点沿路线→→运动. (1)直接写出两点的坐标; (2)设点的运动时间为秒,的面积为,求出与之间的函数关系式; x A O Q P B y (3)当时,求出点的坐标,并直接写出以点为顶点的平行四边形的第四个顶点的坐标. 28.(1)A(8,0)B(0,6) 1分 (2) 点由到的时间是(秒) 点的速度是(单位/秒) 1分 当在线段上运动(或0)时, 1分 当在线段上运动(或)时,, 如图,作于点,由,得, 1分 1分 (自变量取值范围写对给1分,否则不给分.) (3) 1分 3分 注:本卷中各题,若有其它正确的解法,可酌情给分. 25.(本题12分)如图,等腰直角三角形纸片ABC中,AC=BC=4,∠ACB=90º,直角边AC在x轴上,B点在第二象限,A(1,0),AB交y轴于E,将纸片过E点折叠使BE与EA所在直线重合,得到折痕EF(F在x轴上),再展开还原沿EF剪开得到四边形BCFE,然后把四边形BCFE从E点开始沿射线EA平移,至B点到达A点停止.设平移时间为t(s),移动速度为每秒1个单位长度,平移中四边形BCFE与△AEF重叠的面积为S. (1)求折痕EF的长; (2)是否存在某一时刻t使平移中直角顶点C经过抛物线的顶点?若存在,求出t值;若不存在,请说明理由; O C x A C1 F1 E1 B1 B F E y (3)直接写出S与t的函数关系式及自变量t的取值范围. 29.(本小题满分12分)如图,在平面直角坐标系中,□ABCO的顶点O在原点,点A的坐标为(-2,0),点B的坐标为(0,2),点C在第一象限. (1)直接写出点C的坐标; (2)将□ABCO绕点O逆时针旋转,使OC落在y轴的正半轴上,如图②,得□DEFG(点D与点O重合).FG与边AB、x轴分别交于点Q、点P.设此时旋转前后两个平行四边形重叠部分的面积为S0,求S0的值; A (第29题图) B C (D) O E F Q P G x y (3)若将(2)中得到的□DEFG沿x轴正方向平移,在移动的过程中,设动点D的坐标为(t,0),□DEFG与□ABCO重叠部分的面积为S.写出S与t(0<t≤2)的函数关系式.(直接写出结果) 29.解:(1)C(2,2); (2)∵A(-2,0),B(0,2) ∴OA=OB=2 ∴∠BAO=∠ABO=45° ∵□EFGD由□ABCO旋转而成 ∴DG=OA=2,∠G=∠BAO=45° ∵□EFGD ∴FG∥DE ∴∠FPA=∠EDA=90° 在Rt△POG中,OP=OG·sin45°= ∵∠AQP=90°-∠BAO=45° ∴PQ=AP=OA-OP=2- A 图③ B C D O E F N P G x y M K A B C D O E F P G x y 图② M Q N A 图① B C D O E F N P G x y M A 图④ B C D O E F N P G x y M K H S0=(PQ+OB)·OP=(2-+2)·=2-1 (3) 当□DEFG运动到点F在AB上是,如图①,t=2-2 <1>当0<t≤2-2时,如图②,S=-t2+t+2-1 <2>当2-2<t≤时,如图③,S=-t2+4-3 <3>当<t≤2时,如图④,S=-t+4-2 11.在平面直角坐标系中,□ABCD的顶点A、B、D 的坐标分别是(0,0),(5,0),(2,3),则顶点C的 坐标是--------------------------------( ) A.(3,7) B.(5,3) C.(7,3) D.(8,2) .(04)如图11, Rt △OAC是一张放在平面直角坐标系中的直角三角形纸片,点O与原点重合,点A在x轴上,点C在y轴上,OC=,∠CAO=30º.将Rt △OAC折叠,使 OC边落在AC边上,点O与点D重合,折痕为CE. ⑴求折痕CE所在直线的解析式; ⑵求点D的坐标 ⑶设点M为直线CE上的一点,过点M作AC的平行线,交y轴于点N,是否存在这样的点M,使得以M、N、D、C为顶点的四边形是平行四边形?若存在,请求出符合条件的点M的坐标;若不存在,请说明理由. 21.(本小题满分8分)如图,直线y=x+1与双曲线交于A、B两点,其中A点在第一象限.C为x轴正半轴上一点,且S△ABC=3. (1)求A、B、C三点的坐标; A O C x y B (第21题图) (2)在坐标平面内,是否存在点P,使以A、B、C、P为顶点的四边形为平行四边形?若存在,请直接写出点P的坐标,若不存在,请说明理由. 26.(04)(14分)已知,是 边上的中线,分别以所在直线为轴,轴建立直角坐标系(如图). (1)在所在直线上找出一点,使四边形为平行四边形,画出这个平行四边形,并简要叙述其过程; (2)求直线的函数关系式; (第26题) (3)直线上是否存在点,使为等腰三角形?若存在,求点的坐标;若不存在,说明理由. 26.(14分) (1)(4分) 正确画出平行四边形 (2分) 叙述画图过程合理 (4分) 方法一:在直线上取一点,使 连结 (1分) 所以四边形是所画的平行四边形 (2分) 方法二:过画,交直线于 连结 (1分) 所以四边形是所画的平行四边形 (2分) (2)(4分) 是边上的中线 (2分) 设直线的函数关系式:,得 解得 (3分) 直线的函数关系式: (4分) (3)(6分)设 (2分) 分三种情况: ① 解得 (3分) ② 解得 (4分) ③ 解得 ,这时点在上,构不成三角形,舍去. (5分) 综上所述,在直线上存在四点,即,,,,符合题意 (6分) 注:观察图形,能直接得出两点坐标即和可得2分 (一) 3.(本小题满分12分) 如图,在平面直角坐标系中,直线与交于点,分别交轴于点和点,点是直线上的一个动点. (1)求点的坐标. (2)当为等腰三角形时,求点的坐标. (3)在直线上是否存在点,使得以点为顶点的四边形是平行四边形?如果存在,直线写出的值;如果不存在,请说明理由. A y x D C O B 3.解:(1)在中,当时,, ,点的坐标为. 1分 在中,当时,,点的坐标为(4,0). 2分 由题意,得解得 点的坐标为. 3分 A y x y x D2 图(1) 图(2) D1 C D4 D3 M2 M1 O B B O C A D1 D2 E1 E2 M4 (2)当为等腰三角形时,有以下三种情况,如图(1).设动点的坐标为. 由(1),得,. ①当时,过点作轴,垂足为点,则. . ,点的坐标为. 4分 ②当时,过点作轴,垂足为点,则. ,, . 解,得(舍去).此时,. 点的坐标为. 6分 ③当,或时,同理可得. 9分 由此可得点的坐标分别为. 评分说明:符合条件的点有4个,正确求出1个点的坐标得1分,2个点的坐标得3分,3个点的坐标得5分,4个点的坐标得满分;与所求点的顺序无关. (3)存在.以点为顶点的四边形是平行四边形有以下三种情形,如图(2). ①当四边形为平行四边形时,. 10分 ②当四边形为平行四边形时,. 11分 ③当四边形为平行四边形时,. 12分 28.(本小题满分14分)如图,在直角坐标系中,矩形的顶点与坐标原点重合,顶点在坐标轴上,,.动点从点出发,以的速度沿轴匀速向点运动,到达点即停止.设点运动的时间为. (1)过点作对角线的垂线,垂足为点.求的长与时间的函数关系式,并写出自变量的取值范围; (2)在点运动过程中,当点关于直线的对称点恰好落在对角线上时,求此时直线的函数解析式; (3)探索:以三点为顶点的的面积能否达到矩形面积的?请说明理由. y x B C P O A T (第28题图) 28.解:(1)在矩形中,,, .……………………1分 ,. ,即,.……3分 当点运动到点时即停止运动,此时的最大值为. 所以,的取值范围是. 4分 y x B C P O A T (第28题答图2) 2 1 (2)当点关于直线的对称点恰好在对角线上时,三点应在一条直线上(如答图2).……………………5分 ,. , . .点的坐标为.…………6分 设直线的函数解析式为.将点和点代入解析式,得解这个方程组,得 此时直线的函数解析式是. 8分 y x B C P O A T (第28题答图3) E (3)由(2)知,当时,三点在一条直线上,此时点 不构成三角形. 故分两种情况: (i)当时,点位于的内部(如答图3). 过点作,垂足为点,由 可得. . 10分 若,则应有,即. 此时,,所以该方程无实数根. 所以,当时,以为顶点的的面积不能达到矩形面积的. 11分 (ii)当时,点位于的外部.(如答图4) 此时. 12分 若,则应有,即. 解这个方程,得,(舍去). 由于,. 而此时,所以也不符合题意,故舍去. 所以,当时,以为顶点的的面积也不能达到矩形面积的. 综上所述,以为顶点的的面积不能达到矩形面积的. --------14分 25.(本题满分12分) 如图①,OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在轴的正半轴上,点C在轴的正半轴上,OA=5,OC=4. (1)在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,求D、E两点的坐标; (2)如图②,若AE上有一动点P(不与A、E重合)自A点沿AE方向向E点匀速运动,运动的速度为每秒1个单位长度,设运动的时间为秒,过P点作ED的平行线交AD于点M,过点M作AE的平行线交DE于点N.求四边形PMNE的面积S与时间之间的函数关系式;当取何值时,S有最大值?最大值是多少? (3)在(2)的条件下,当为何值时,以A、M、E为顶点的三角形为等腰三角形,并求出相应时刻点M的坐标. 图① E O D C B A 图② O A E D C B P M N · 25.解:(1)依题意可知,折痕AD是四边形OAED的对称轴, ∴在中, ∴ ∴ ∴点坐标为………………………………………………………(2分) 在中, 又∵ ∴ 解得: ∴点坐标为………………………………………………………(3分) (2)如图①∵∥ ∴ ∴ 又知 ∴ 又∵ 而显然四边形为矩形 ∴…………………(5分)∴ 又∵ ∴当时,有最大值(面积单位)…………………(6分) (3)(i)若(如图①) 在中,,∴为的中点 又∵∥ , ∴为的中点 ∴ ∴ ∴ 又∵与是关于对称的两点 ∴ , ∴当时(),为等腰三角形 此时点坐标为………………………………………………(9分) (ii)若(如图②) 在中, ∵∥ ,∴,∴ ∴ ∴ 同理可知: , ∴当时(),此时点坐标为 综合(i)、(ii)可知:或时,以A、M、E为顶点的三角形为等腰三角形,相应M点的坐标为或………………………………………(12分) O x y (第24题) C B E D 24.如图,四边形是一张放在平面直角坐标系中的矩形纸片,点在轴上,点在轴上,将边折叠,使点落在边的点处.已知折叠,且. (1)判断与是否相似?请说明理由; (2)求直线与轴交点的坐标; (3)是否存在过点的直线,使直线、直线与轴所围成的三角形和直线、直线与轴所围成的三角形相似?如果存在,请直接写出其解析式并画出相应的直线;如果不存在,请说明理由. O x y (第24题图1) C B E D 3 1 2 A 24.解:(1)与相似. 理由如下: 由折叠知,, , 又, . (2),设, 则. 由勾股定理得. . (第24题图2) O x y C B E D P M G l N A F 由(1),得, , . 在中,, ,解得. ,点的坐标为, 点的坐标为, 设直线的解析式为, 解得 ,则点的坐标为. (3)满足条件的直线有2条:, . 如图2:准确画出两条直线. 28.(本小题满分10分) 如图,平面上一点从点出发,沿射线方向以每秒1个单位长度的速度作匀速运动,在运动过程中,以为对角线的矩形的边长;过点且垂直于射线的直线与点同时出发,且与点沿相同的方向、以相同的速度运动. (1)在点运动过程中,试判断与轴的位置关系,并说明理由. (2)设点与直线都运动了秒,求此时的矩形与直线在运动过程中所扫过的区域的重叠部分的面积(用含的代数式表示). x y O l B P M A 28.解:(1)轴. 1分 理由:中,,. 2分 设交于点,交轴于点,矩形的对角线互相平分且相等,则, ,过点作轴于,则,,,,轴. 3分 (2)设在运动过程中与射线交于点,过点且垂直于射线的直线交于点,过点且垂直于射线的直线交于点,则. ,,,,. 4分 ①当,即时,. 6分 ②当,即时,设直线交于,交于,则,,, . 8分 ③当,即时,, ………………………………………………10分 24.(本小题满分6分)推理运算 如图,在直角坐标系中,直线与轴,轴分别交于两点,以 为边在第二象限内作矩形,使. (1)求点,点的坐标,并求边的长; x y O A B C D H (2)过点作轴,垂足为,求证:; (3)求点的坐标. 24.(1),, 在中,. (2分) (2)由,, ,又, . (4分) (3), ,即, ,. . (6分) 22. (本题满分12分) (1)S1 = S2 证明:如图10,∵ FE⊥轴,FG⊥轴,∠BAD = 90°, ∴ 四边形AEFG是矩形 . ∴ AE = GF,EF = AG . ∴ S△AEF = S△AFG ,同理S△ABC = S△ACD . ∴ S△ABC-S△AEF = S△ACD-S△AFG . 即S1 = S2 . (2)∵FG∥CD , ∴ △AFG ∽ △ACD . ∴ . ∴ FG = CD, AG =AD . ∵ CD = BA = 6, AD = BC = 8 , ∴ FG = 3,AG = 4 . ∴ F(4,3)。 (3)解法一:∵ △A′E′F′是由△AEF沿直线AC平移得到的 , ∴ E′A′= E A = 3,E′F′= E F = 4 .① 如图11-1 ∵ 点E′到轴的距离与到轴的距离比是5∶4 , 若点E′在第一象限 , 图11-1 ∴设E′(4, 5)且 > 0 , 延长E′A′交轴于M ,得A′M = 5-3, AM = 4. ∵ ∠E′=∠A′M A = 90°, ∠E′A′F′=∠ M A′A , ∴ △ E′A′F′∽△ M A′A ,得 . ∴ . ∴ = ,E′( 6, ) . 图11-2 ② 如图11-2 ∵ 点E′到轴的距离与到轴的距离比是5∶4 , 若点E′在第二象限,∴设E′(-4, 5)且 > 0, 得NA = 4, A′N = 3 - 5, 同理得△A′F′E′∽ △A′AN . ∴ , . ∴ a = , ∴ E′(, ) . 图11-3 ③ 如图11-3 ∵ 点E′到轴的距离与到轴的距离比是5∶4 , 若点E′在第三象限,∴设E′( -4,- 5 )且 > 0. 延长E′F′交轴于点P,得AP = 5, P F′= 4 - 4 . 同理得△A′E′F′∽△A P F′ ,得, .∴ = (不合舍去). ∴ 在第三象限不存在点E′. ④ 点E′不可能在第四象限 . ∴ 存在满足条件的E′坐标分别是( 6, ) 、(, ) . 图11-4 解法二:如图11-4,∵△A′E′F′是由△AEF沿直线AC平移得到的,且A′、F′两点始终在直线AC上, ∴ 点E′在过点E(0,3)且与直线AC平行的直线l上移动. ∵ 直线AC的解析式是, ∴ 直线l的解析式是 . 根据题意满足条件的点E′的坐标设为(4, 5)或( -4,5)或( -4,-5),其中 > 0 . ∵点E′在直线l上 , ∴ 或 或 解得(不合舍去). ∴ E′(6, )或E′(, ). ∴ 存在满足条件的E′坐标分别是( 6 , ) 、(, ) . 解法三: ∵ △A′E′F′是由△AEF沿直线AC平移得到的,且A′、F′两点始终在直线AC上 , ∴ 点E′在过点E(0,3)且与直线AC平行的直线l上移动 . ∵ 直线AC的解析式是 , ∴ 直线L的解析式是. 设点E′为(, ) ∵ 点E′到轴的距离与到轴的距离比是5︰4 ,∴ . ① 当、为同号时,得 解得 ∴ E′(6, 7.5). ② 当、为异号时,得 解得 ∴ E′(, ). ∴存在满足条件的E′坐标分别是( 6, ) 、( , ) . 26.如图,在平面直角坐标系中,直线(b>0)分别交x轴、y轴于A、B两点,以OA、OB为边作矩形OACB,D为BC的中点.以M(4,0),N(8,0)为斜边端点作等腰直角三角形PMN,点P在第一象限,设矩形OACB与△PMN重叠部分的面积为S. (1)求点P的坐标; (2)当b值由小到大变化时,求S与b的函数关系式; (3)若在直线(b>0)上存在点Q,使∠OQM等于90°,请直接写出b的取值范围; A B C M N D P O y x (第26题图) (4)在b值的变化过程中,若△PCD为等腰三角形,请直接写出所有符合条件的b值. 24.(本题14分) 如图1,在平面直角坐标系中,已知点,点在正半轴上,且.动点在线段上从点向点以每秒个单位的速度运动,设运动时间为秒.在轴上取两点作等边. (1)求直线的解析式; (2)求等边的边长(用的代数式表示),并求出当等边的顶点运动到与原点重合时的值; (3)如果取的中点,以为边在内部作如图2所示的矩形,点在线段上.设等边和矩形重叠部分的面积为,请求出当秒时与的函数关系式,并求出的最大值. (图1) (图2) 24.(本题14分) 解:(1)直线的解析式为:. (2)方法一,,,, ,, 是等边三角形,, ,. 方法二,如图1,过分别作轴于,轴于, (图1) 可求得, , (图2) , 当点与点重合时, , . , (图3) . (3)①当时,见图2. 设交于点, 重叠部分为直角梯形, 作于. ,, , , , , , , . 随的增大而增大, 当时,. ②当时,见图3. 设交于点, 交于点,交于点, 重叠部分为五边形. 方法一,作于,, , , . 方法二,由题意可得,,,, 再计算 , . (图4) ,当时,有最大值,. ③当时,,即与重合, 设交于点,交于点,重叠部 分为等腰梯形,见图4. , 综上所述:当时,; 当时,; 当时,. , 的最大值是. 27.(本题满分12分) 如图,在平面直角坐标系中,已知矩形的边分别在轴上和轴上,线段的长分别是一元二次方程的两个根,且;点从点开始沿边匀速移动,点从点开始沿边匀速移动.如果点,点同时出发,它们移动的速度相同,设,设的面积为. (1)求与的函数关系式; (2)连结矩形的对角线,当为何值时,以为顶点的三角形与相似; (3)当的面积最大时,将沿所在直线翻折后得到,试判断点是否在矩形的对角线上,请说明理由. 23.(本题满分12分) 如图,平面直角坐标系中,四边形为矩形,点的坐标分别为,动点分别从同时出发,以每秒1个单位的速度运动.其中,点沿向终点运动,点沿向终点运动,过点作,交于,连结,已知动点运动了秒. (1)点的坐标为( , )(用含的代数式表示); (2)试求面积的表达式,并求出面积的最大值及相应的值; (3)当为何值时,是一个等腰三角形?简要说明理由. N B A M P C O (第23题图) 23.(本小题满分12分) 解:(1)由题意可知,,, 点坐标为. 2分 (2)设的面积为,在中,,边上的高为,其中. 3分 . 5分 的最大值为,此时. 7分 (3)延长交于,则有. N B A M P C O (第23题图) Q ①若, . , .……………………………………9分 ②若,则, . 10分 ③若,则. , 在中,. ,. 11分 综上所述,,或,或. (第15题) 15.如图,把矩形纸片放入平面直角坐标系中,使,分别落在轴,轴上,连结,将纸片沿折叠,使点落在点的位置.若,,则点的坐标为____________. 26、已知,如图,在直角坐标系中,矩形OABC的对角线AC所在直线解析式为 (l)在x轴上存在这样的点M,使AMAB为等腰三角形,求出所有符合要求的点M的坐 标;(2)动点P从点C开始在线段CO上以每秒个单位长度的速度向点O移动,同时,动点 Q从点O开始在线段OA上以每秒1个单位长度的速度向点A移动.设P、Q移动的时间为t秒. ①是否存在这样的时刻2,使△OPQ与ABCP相似,并说明理由; ②设△BPQ的面积为S,求S与t间的函数关系式,并求出t为何值时,S有最小值. 22.(本题满分14分)如图,在平面直角坐标系中,四边形OABC为矩形,点A、B的坐标分别为(4,0)、(4,3),动点M、N分别从点O、B同时出发,以每秒1个单位的速度运动,其中点M沿OA向终点A运动,点N沿BC向终点C运动,过点N作NP⊥BC,交AC于点P,连结MP,当两动点运动了t秒时。 (1)P点的坐标为( , )(用含t的代数式表示); (2)记△MPA的面积为S,求S与t的函数关系式(0<t<4); (3)当t= 秒时,S有最大值,最大值是 ; (4)若点Q在y轴上,当S有最大值且△QAN为等腰三角形是,求直线AQ的解析式。 O C N M P B(4,3) A(4,0) y x 24.将一矩形纸片放在平面直角坐标系中,,,.动点 从点出发以每秒1个单位长的速度沿向终点运动,运动秒时,动点从点出发以相等的速度沿向终点运动.当其中一点到达终点时,另一点也停止运动.设点的运动时间为(秒). (1)用含的代数式表示; (2)当时,如图1,将沿翻折,点恰好落在边上的点处,求点的坐标; (3)连结,将沿翻折,得到,如图2.问:与能否平行?与能否垂直?若能,求出相应的值;若不能,说明理由. 图1 O P A x B D C Q y (第24题图) 图2 O P A x B C Q y E 24.(本题满分14分) 解:(1),. 图1 O P A x B D C Q y 图2 O P A x B C Q y 图3 O F A x B C y E Q P (2)当时,过点作,交于,如图1, 则,, ,. (3)①能与平行. 若,如图2,则, 即,,而, . ②不能与垂直. 若,延长交于,如图3, 则. . . 又,, , ,而, 不存在. O (第24题图) (A) D C D x y 5.(本题满分12分)如图,在平面直角坐标系xoy中,已知矩形ABCD的边AB、AD分别在x轴、y轴上,点A与坐标原点重合,且AB=2,AD=1。 操作:将矩形ABCD折叠,使点A落在边DC上。 探究:(1)我们发现折痕所在的直线与矩形的两边一定相交,那么相交的情形有几种?请你画出每种情形的图形;(只要用矩形草稿纸动手折一折你会有发现的!) (2)当折痕所在的直线与矩形的边OD相交于点E,与边OB相交于点F时,设直线的解析式为y=kx+b。 ①求b与k的函数关系式; ②求折痕EF的长(用含k的代数式表示),并写出k的取值范围。 6. (04)将一矩形纸片OABC放在直角坐标系中,O为原点,C在轴上,OA=6,OC=10. ⑴如图⑴,在OA上取一点E,将△EOC沿EC折叠,使O点落在AB边上的D点,求E点的坐标; 第29题图(1) B C D E A ⑵如图⑵,在OA、OC边上选取适当的点E′、F,将△E′OF沿E′F折叠,使O点落在AB边上的D′点,过D′作D′G∥A′O交E′F于T点,交OC′于G点,求证:TG=A′E′ ⑶在⑵的条件下,设T(,)①探求:与之间的函数关系式.②指出变量的取值范围. 第29题图(2)2 T C' F' E' B' D' A' G ⑷如图⑶,如果将矩形OABC变为平行四边形OA"B"C",使O C"=10,O C"边上的高等于6,其它条件均不变,探求:这时T(,)的坐标与之间是否仍然满足⑶中所得的函数关系,若满足,请说明理由;若不满足,写出你认为正确的函数关系式. D" 第29题图(3) A" E" T' F" G' C" B" 7.已知在矩形ABCD中,AB=4,BC=,O为BC上一点,BO=,如图所示,以BC所在直线为x轴,O为坐标原点建立平面直角坐标系,M为线段OC上的一点. (1)若点M的坐标为(1,0),如图①,以OM为一边作等腰△OMP,使点P在矩形ABCD的一边上,则符合条件的等腰三角形有几个?请直接写出所有符合条件的点P的坐标; (2)若将(1)中的点M的坐标改为(4,0),其它条件不变,如图②,那么符合条件的等腰三角形有几个?求出所有符合条件的点P的坐标; (3)若将(1)中的点M的坐标改为(5,0),其它条件不变,如图③,请直接写出符合条件的等腰三角形有几个.(不必求出点P的坐标) 第24题图 24.解:(1)符合条件的等腰△OMP只有1个.点P的坐标为(,4) ……2分 (2)符合条件的等腰△OMP有4个. …………………………………………3分 如图①,在△OP1M中,OP1=OM=4, 在Rt△OBP1中,BO=, BP1=== ∴P1(-,) ……………………………………………………………………5分 在Rt△OMP2中,OP2=OM=4,∴P2(0,4) 在△OMP3中,MP3=OP3, ∴点P3在OM的垂直平分线上,∵OM=4,∴P3(2,4) 在Rt△OMP4中,OM=MP4=4,∴P4(4,4) …………………………………9分 (3)若M(5,0),则符合条件的等腰三角形有7个. …………………………12分 点P的位置如图②所示 24.(本题(1)~(3)小题满分12分,(4)小题为附加题另外附加2分) 如图①,正方形 ABCD中,点A、B的坐标分别为(0,10),(8,4),点C在第一象限.动点P在正方形 ABCD的边上,从点A出发沿A→B→C→D匀速运动,同时动点Q以相同速度在x轴上运动,当P点到D点时,两点同时停止运动,设运动的时间为t秒. (1) 当P点在边AB上运动时,点Q的横坐标(长度单位)关于运动时间t(秒)的函数图象如图②所示,请写出点Q开始运动时的坐标及点P运动速度; (2) 求正方形边长及顶点C的坐标; (第24题图①) (第24题图②) (3) 在(1)中当t为何值时,△OPQ的面积最大,并求此时P点的坐标. (1) 附加题:(如果有时间,还可以继续 解答下面问题,祝你成功!) 如果点P、Q保持原速度速度不 变,当点P沿A→B→C→D匀 速运动时,OP与PQ能否相等, 若能,写出所有符合条件的t的 值;若不能,请说明理由. 24.解:(1)(1,0) ----------------------------------------------------------------------------------1分 点P运动速度每秒钟1个单位长度.----------------------------------------------3分 (2) 过点作BF⊥y轴于点,⊥轴于点,则=8,. ∴. 在Rt△AFB中,.-----------------------------------------------5分 过点作⊥轴于点,与的延长线交于点. ∵ ∴△ABF≌△BCH. ∴. ∴. ∴所求C点的坐标为(14,12).------------7分 (3) 过点P作PM⊥y轴于点M,PN⊥轴于点N, 则△APM∽△ABF. ∴. . ∴. ∴. 设△OPQ的面积为(平方单位) ∴(0≤≤10) --------------------10分 说明:未注明自变量的取值范围不扣分. ∵<0 ∴当时, △OPQ的面积最大.------------------11分 此时P的坐标为(,) . ---------------------------------------------------12分 (4) 当 或时, OP与PQ相等.-----------------------------------------14分 对一个加1分,不需写求解过程. 2.(本题10分) 如图,平面直角坐标系中有一个边长为2的 正方形,M为OB的中点,将△沿直线AM对折,使O点落在处,连结,过点作于N. A C O B M N D x y (1)写出点A、B、C的坐标; (2)判断△与△是否相似,若是,请给出证明; (3)求点的坐标. 2. (1)∵OA=OB=2 A C O B M N D x y 1 2 3 ∴ …3分 (2)△∽△ …4分 证:∵四边形是正方形 ∴ 又⊥ ∴ ∴ 又根据对称性质可知: 于D点 ∴在Rt△ODM中, 在Rt△AOM中, ∴ ∴△∽△ …6分 (3)∵M是OB的中点 ∴ ∴在Rt△中, 又∵OD是Rt△斜边上的高 ∴ ∴ ……8分 又∵△∽△ ∴ ∴ ∴ ………10分 27.(14分)在直角坐标系中,O为坐标原点,点A的坐标为(2,2),点C是线段OA上的一个动点(不运动至O,A两点),过点C作CD⊥x轴,垂足为D,以CD为边作如图所示的正方形CDEF.连接AF并延长交x轴的正半轴于点B,连接OF. (1)猜想OD和DE之间的数量关系,并说明理由; (2)设OD=t,求OB的长(用含t的代数式表示); (3)若点B在E的右侧时,△BFE与△OFE能否相似?若能,请你求出此时经过O,A,B三点的抛物线解析式;若不能,请说明理由. O B A C F E D x y 第27题图 24. 如图,边长为1的正方形OABC的顶点O为坐标原点,点A在x轴的正半轴上,点C在y轴的正半轴上.动点D在线段BC上移动(不与B,C重合),连接OD,过点D作DE⊥OD,交边AB于点E,连接OE.记CD的长为t. (1) 当t=时,求直线DE的函数表达式; (2) 如果记梯形COEB的面积为S,那么是否存在S的最大值?若存在,请求出这个最大值及此时t的值;若不存在,请说明理由; (3) 当OD2+DE 2的算术平方根取最小值时, 求点E的坐标. 24. 解:(1)易知△CDO∽△BED, 所以,即,得BE=,则点E 的坐标为E(1,).……………………………(2分) 设直线DE的一次函数表达式为y=kx+b,直线经过两点D(,1)和E(1,),代入y=kx+b得,,故所求直线DE的函数表达式为y=.…………………………(2分) (注:用其它三角形相似的方法求函数表达式,参照上述解法给分) (2) 存在S的最大值.……………………………………………………………1分 求最大值:易知△COD∽△BDE,所以,即,BE=t-t2, 1分 ×1×(1+t-t2).……………………………………1分 故当t=时,S有最大值.………………………………………………2分 (3) 在Rt△OED中,OD2+DE 2=OE2,OD2+DE 2的算术平方根取最小值,也就是斜边OE取最小值.……………………………………………………………1分 当斜边OE取最小值且一直角边OA为定值时,另一直角边AE达到最小值,1分 于是△OEA的面积达到最小值,…………………………………………1分 此时,梯形COEB的面积达到最大值.………………………………………1分 由(2)知,当t=时,梯形COEB的面积达到最大值,故所求点E的坐标是 (1,).…………………………………………………………………1分 注:(3)小题的另一种解法:=,猜想当t=时,取最小值(其值为).……………………………………………1分 运用计算器可以验证猜想是正确的,………………………………………………3分 此时点E的坐标是(1,).………………………………………………1分 22.(本小题12分)如图,边长为4的正方形OABC的顶点O为坐标原点,点A在x轴的正半轴上,点C在y轴的正半轴上.动点D在线段BC上移动(不与B,C重合),连接OD,过点D作DE⊥OD,交边AB于点E,连接OE. (1)当CD=1时,求点E的坐标; (2)如果设CD=t,梯形COEB的面积为S,那么是否存在S的最大值?若存在,请求出这个最大值及此时t的值;若不存在,请说明理由. 22.(本小题12分) 解:(1) 正方形OABC中,因为ED⊥OD,即∠ODE =90° 所以∠CDO+∠EDB=90°,即∠COD=90°-∠CDO,而 ∠EDB =90°-∠CDO, 所以∠COD =∠EDB 又因为∠OCD=∠DBE=90° 所以△CDO∽△BED, 所以,即,得BE=, 则: 因此点E的坐标为(4,). (2) 存在S的最大值. 由△CDO∽△BED, 所以,即,BE=t-t2, ×4×(4+t-t2). 故当t=2时,S有最大值10. 16.如图,正方形的边长为10,点E在CB的延长线上,,点P在边CD上运动(C、D两点除外),EP与AB相交于点F,若,四边形的面积为,则关于的函数关系式是 . P D C B F A E 12.如图,在平面直角坐标系中,OABC是正方形,点A的坐标是(4,0),点P为边AB上一点,∠CPB=60 °,沿CP折叠正方形,折叠后,点B落在平面内点B’处,则B’点的坐标为( ). A、(2,) B、(,) C、(2,) D、(,) A B C P 60° B’ y O x (第12题图) y x O C1 B2 A2 C3 B1 A3 B3 A1 C2 (第16题图) 16.正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图所示的方式放置.点A1,A2,A3,…和点C1,C2,C3,…分别 在直线(k>0)和x轴上, 已知点B1(1,1),B2(3,2), 则Bn的坐标是______________. 15.如图所示,直线y=x+1与y轴相交于点A1,以OA1为边作正方形OA1B1C1,记作第一个正方形;然后延长C1B1与直线y=x+1相交于点A2,再以C1A2为边作正方形C1A2B2C2,记作第二个正方形;同样延长C2B2与直线y=x+1相交于点A3,再以C2A3为边作正方形C2A3B3C3,记作第三个正方形;…依此类推,则第n个正方形的边长为________________. A1 A2 A3 A4 B1 B2 B3 B4 x y=x+1 O C1 C2 C3 C4 (第15题图) y 26.(04)如图,四边形是一张放在平面直角坐标系中的正方形纸片.点与坐标原点重合,点在轴上,点在轴上,,点为的中点,点的坐标为 ,过点且平行于轴的直线与交于点.现将纸片折叠,使顶点落在上,并与上的点重合,折痕为,点为折痕与轴的交点. (1)求点的坐标; (2)求折痕所在直线的解析式; (3)设点为直线上的点,是否存在这样的点,使得以为顶点的三角形为等腰三角形,若存在,请直接写出点的坐标;若不存在,请说明理由. (第26题图) 26.解:(1)四边形是正方形,,为中点, 轴,,且 而, (2分) , (5分) (2) , (7分) 设直线的解析式: 折痕所在直线解析式: (10分) (3), (14分) 27.(本题 10分) 如图,在平面直角坐标系中,点O是坐标原点,四边形AOCB是梯形,AB∥OC,点A的坐标为(0,8),点C的坐标为(10,0),OB=OC. (1)求点B的坐标; (2)点P从C点出发,沿线段CO以5个单位/秒的速度向终点O匀速运动,过点P作PH⊥OB,垂足为H,设△HBP的面积为S(S≠0),点P的运动时间为t秒,求S与t之间的函数关系式(直接写出自变量t的取值范围); (3)在(2)的条件下,过点P作PM∥CB交线段AB于点M,过点M作MR⊥OC,垂足为R,线段MR分别交直线PH、OB于点E、G,点F为线段PM的中点,连接EF,当t为何值时,? 22.(本题满分9分)将两块大小一样含30°角的直角三角板,叠放在一起,使得它们的斜边 AB重合,直角边不重合,已知AB=8,BC=AD=4,AC与BD相交于点E,连结CD. (1)填空:如图9,AC= ,BD= ;四边形ABCD是 梯形. (2)请写出图9中所有的相似三角形(不含全等三角形). (3)如图10,若以AB所在直线为轴,过点A垂直于AB的直线为轴建立如图10的平面直角坐标系,保持ΔABD不动,将ΔABC向轴的正方向平移到ΔFGH的位置,FH与BD相交于点P,设AF=t,ΔFBP面积为S,求S与t之间的函数关系式,并写出t的取值值范围. D C B A E 图9 E D C H F G B A P y x 图10 10 22.解:(1),,…………………………1分 等腰;…………………………2分 (2)共有9对相似三角形.(写对3-5对得1分,写对6-8对得2分,写对9对得3分) ①△DCE、△ABE与△ACD或△BDC两两相似,分别是:△DCE∽△ABE,△DCE∽△ACD,△DCE∽△BDC,△ABE∽△ACD,△ABE∽△BDC;(有5对) ②△ABD∽△EAD,△ABD∽△EBC;(有2对) ③△BAC∽△EAD,△BAC∽△EBC;(有2对) 所以,一共有9对相似三角形.…………………………………………5分 K (3)由题意知,FP∥AE, ∴ ∠1=∠PFB, 又∵ ∠1=∠2=30°, ∴ ∠PFB=∠2=30°, ∴ FP=BP.…………………………6分 过点P作PK⊥FB于点K,则. ∵ AF=t,AB=8, ∴ FB=8-t,. 在Rt△BPK中,. ……………………7分 ∴ △FBP的面积, ∴ S与t之间的函数关系式为: ,或. …………………………………8分 t的取值范围为:. …………………………………………………………9分 24.如图1所示,直角梯形OABC的顶点A、C分别在y轴正半轴与轴负半轴上.过点B、C作直线.将直线平移,平移后的直线与轴交于点D,与轴交于点E. (1)将直线向右平移,设平移距离CD为(t0),直角梯形OABC被直线扫过的面积(图中阴影部份)为,关于的函数图象如图2所示, OM为线段,MN为抛物线的一部分,NQ为射线,N点横坐标为4. ①求梯形上底AB的长及直角梯形OABC的面积; ②当时,求S关于的函数解析式; (2)在第(1)题的条件下,当直线向左或向右平移时(包括与直线BC重合),在直线AB上是否存在点P,使为等腰直角三角形?若存在,请直接写出所有满足条件的点P的坐标;若不存在,请说明理由. 24.解: (1)① ……………………………………………………………………………2分 ,,S梯形OABC=12 ……………………………………………2分 ②当时, 直角梯形OABC被直线扫过的面积=直角梯形OABC面积-直角三角开DOE面积 …………………………………………4分 (2) 存在 ……………………………………………………………………………………1分 …(每个点对各得1分)……5分 对于第(2)题我们提供如下详细解答(评分无此要求).下面提供参考解法二: ① 以点D为直角顶点,作轴 设.(图示阴影) ,在上面二图中分别可得到点的生标为P(-12,4)、P(-4,4) E点在0点与A点之间不可能; ② 以点E为直角顶点 同理在②二图中分别可得点的生标为P(-,4)、P(8,4)E点在0点下方不可能. ③ 以点P为直角顶点 同理在③二图中分别可得点的生标为P(-4,4)(与①情形二重合舍去)、P(4,4), E点在A点下方不可能. 综上可得点的生标共5个解,分别为P(-12,4)、P(-4,4)、P(-,4)、 P(8,4)、P(4,4). 下面提供参考解法二: 以直角进行分类进行讨论(分三类): 第一类如上解法⑴中所示图 ,直线的中垂线方程:,令得.由已知可得即化简得解得 ; 第二类如上解法②中所示图 ,直线的方程:,令得.由已知可得即化简得解之得 , 第三类如上解法③中所示图 ,直线的方程:,令得.由已知可得即解得 (与重合舍去). 综上可得点的生标共5个解,分别为P(-12,4)、P(-4,4)、P(-,4)、 P(8,4)、P(4,4). 事实上,我们可以得到更一般的结论: 如果得出设,则P点的情形如下 直角分类情形 ; 26.(12分)如图,梯形ABCD中,AD∥BC,AB⊥BC,已知AD=8,BC=12,AB=4.动点E从点B出发,沿射线BA以每秒3个单位的速度移动;同时动点F从点A出发,在线段AD上以每秒2个单位的速度向点D移动.当点F与点D重合时,E 、F两点同时停止移动.设点E移动时间为t秒. (1)求当t为何值时,三点C、E、F共线? (2)设顺次连结四点B、C、F、E所得封闭图形的面积为S,求出S与t之间的函数关系(要求写出t的取值范围);并求当S取最大值时tan∠BEF的值. (3)求当t为何值时,以B、E、F为顶点的三角形是等腰三角形? 25.(本小题10分)如图所示,在平面直角坐标中,四边形OABC是等腰梯形,CB∥OA,OA=7,AB=4,∠COA=60°,点P为x轴上的—个动点,点P不与点0、点A重合.连结CP,过点P作PD交AB于点D. (1)求点B的坐标; (2)当点P运动什么位置时,△OCP为等腰三角形,求这时点P的坐标; (3)当点P运动什么位置时,使得∠CPD=∠OAB,且,求这时点P的坐标. O y P C B D A x y O P C B D A x Q 25.(本小题10分) (1)过B作BQ⊥OA于Q则∠COA=∠BAQ=60° 在Rt△BQA中, QB=ABSin60°= ∴OQ=OA-QA=5 ∴B(5,) D O y P C B A x P (2)若点P在x正半轴上 ∵∠COA=60°,△OCP为等腰三角形 ∴△OCP是等边三角形 ∴OP=OC=CP=4 ∴P(4,0) 若点P在x负半轴上 ∵∠COA=60° ∴∠COP=120° ∴△OCP为顶角120°的等腰三角形 ∴OP=OC=4 ∴P(-4,0) ∴点P的坐标为(4,0)或(-4,0) (3)∵∠CPD=∠OAB=∠COP=60° O y P C B D A x ∴∠OPC+∠DPA=120° 又∵∠PDA+∠DPA=120° ∴∠OPC=∠PDA ∵∠OCP=∠A=60° ∴△COP∽△PAD ∴ ∵,AB=4 O y P C B D A x ∴BD= ∴AD= 即 ∴ 得OP=1或6 x ∴P点坐标为(1,0)或(6,0) 25.(本小题满分6分) 小明在研究苏教版《有趣的坐标系》后,得到启发,针对正六边形OABCDE,自己设计了一个坐标系如图,该坐标系以O为原点,直线OA为轴,直线OE为轴,以正六边形OABCDE的边长为一个单位长。坐标系中的任意一点P用一有序实数对()来表示,我们称这个有序实数对()为点P的坐标。坐标系中点的坐标的确定方法如下: (ⅰ)轴上点M的坐标为(),其中为M点在轴上表示的实数; (ⅱ)轴上点N的坐标为(),其中为N点在)轴上表示的实数; (ⅲ)不在、轴上的点Q的坐标为(),其中为过点Q且与轴平行的直线与轴的交点在轴上表示的实数,为过点Q且与轴平行的直线与轴的交点在轴上表示的实数。 则:(1)分别写出点A、B、C的坐标 (2)标出点M(2,3)的位置; (3)若点为射线OD上任一点,求与所满足的关系式。 。 28.(本题10分) 如图,梯形在平面直角坐标系中,上底平行于轴,下底交轴于点,点(4,),点,,. (1)求直线的解析式; (2)若点的坐标为,动点从出发,以1个单位/秒的速度沿着边向点运动(点可以与点或点重合),求的面积()随动点的运动时间秒变化的函数关系式(写出自变量的取值范围); (3)在(2)的条件下,当秒时,点停止运动,此时直线与轴交于点.另一动点开始从出发,以1个单位/秒的速度沿着梯形的各边运动一周,即由到,然后由到,再由到,最后由回到(点可以与梯形的各顶点重合).设动点的运动时间为秒,点为直线上任意一点(点不与点重合),在点的整个运动过程中,求出所有能使与相等的的值. (第28题图) (第28题备用图) 24.已知:在四边形中,,分别是上的点, 且.设四边形的面积为,. (1)如图1,当四边形为正方形时, ①求关于的函数解析式,并求的最小值; ②在图2中画出①中函数的草图,并估计时的近似值(精确到0.01); (2)如图3,当四边形为菱形,且时,四边形的面积是否存在最小值?若存在,求出最小值;若不存在,请说明理由. 方格边长0.1 第24题图2 第24题图1 第24题图3 24.(1)①解:在中,, , 则 第24题图2 方格边长0.1 . 3分 当时,. 4分 0 0.3 0.5 0.7 1 0.58 0.5 0.58 1 ②列表: 在直角坐标系中描点、画图(图2中粗线). 6分 (注:作图时,不列对应值表不扣分) 观察函数的图象,可知当时,和. 7分 验证:当时,;当时,. 从而取.同理取. 8分 (2)四边形的面积存在最小值. 理由如下: 由条件,易证,. 9分 第24题图3 作于,作且交的延长线于. ,则,又在中, , .同理得. , . 11分 又,. 当时,四边形的面积存在最小值. 12分 25、如图,正方形ABCD的边长为5cm,Rt△EFG中,∠G=90°,FG=4cm,EG=3cm,且点B、F、C、G在直线上,△EFG由F、C重合的位置开始,以1cm/秒的速度沿直线按箭头所表示的方向作匀速直线运动. (1)当△EFG运动时,求点E分别运动到CD上和AB上的时间; (2)设x(秒)后,△EFG与正方形ABCD重合部分的面积为y(cm),求y与x的函数关系式; (3)在下面的直角坐标系中,画出0≤x≤2时(2)中函数的大致图象;如果以O为圆心的圆与该图象交于点P(x,),与x轴交于点A、B(A在B的左侧),求∠PAB的度数. 26、如图:正方形ABCO的边长为3,过A点作直线AD交x轴于D点,且D点的坐标为(4,0),线段AD上有一动点,以每秒一个单位长度的速度移动。 (1)求直线AD的解析式; (2)若动点从A点开始沿AD方向运动2.5秒时到达的位置为点P,求经过B、O、P三点的抛物线的解析式; (3)若动点从A点开始沿AD方向运动2.5秒时到达的位置为点P1,过P1作P1E⊥x轴,垂足为E,设四边形BCEP1的面积为S,请问S是否有最大值?若有,请求出来;若没有,请说明理由。 2.在平面直角坐标系中,已知点A(0,2),B(,0),C(0,),D(,0),则以这四个点为顶点的四边形是( ) A.矩形 B.菱形 C.正方形 D.梯形 A.1个 B.2个 C.3个 D.4个 1.如图,当四边形的周长最小时, . y x P(a,0) N(a+2,0) A(1,-3) (4题图) B(4,-1) O A B C 第10题 D E · · O G · F x y 2.如图,已知在直角梯形AOBC中,AC∥OB,CB⊥OB,OB=18,BC=12,AC=9,对角线OC、AB交于点D,点E、F、G分别是CD、BD、BC的中点.以O为原点,直线OB为x轴建立平面直角坐标系,则G、E、D、F四个点中与点A在同一反比例函数图象上的是() A.点G B.点E C.点D D.点F 5.已知直线(n是不为零的自然数)。当n=1时,直线与x轴和y轴分别交于点A1和B1,设△A1OB1(其中O是平面直角坐标系的原点)的面积为S1;当n=2时,直线与x轴和y轴分别交于点A2和B2,设△A2OB2的面积为S2,…, 依此类推,直线与x轴和y轴分别交于点,设的面积为. (1) 求设△A1OB1的面积S1; (2) 求的值. 6.(2010年顺义)如图,直线:平行于直线,且与直线:相交于点.(1)求直线、的解析式; (2)直线与y轴交于点A.一动点从点A出发,先沿平行于x轴的方向运动,到达直线上的点处后,改为垂直于x轴的方向运动,到达直线上的点处后,再沿平行于x轴的方向运动,到达直线上的点处后,又改为垂直于x轴的方向运动,到达直线上的点处后,仍沿平行于x轴的方向运动,…… 照此规律运动,动点依次经过点,,,,,,…,,,… ①求点,,,的坐标; ②请你通过归纳得出点、的坐标;并求当动点到达处时,运动的总路径的长. 解:(1)由题意,得 解得 ∴直线的解析式为 . ………………………………… 1分 ∵点在直线上, ∴. ∴. ∴直线的解析式为 . ……………………………… 2分 (2)① A点坐标为 (0,1), 则点的纵坐标为1,设, ∴. ∴. ∴点的坐标为 . ………………………………………… 3分[来源:学§科§网] 则点的横坐标为1,设 ∴. ∴点的坐标为 . ………………………………………… 4分 同理,可得 ,. ……………………………… 6分 ②经过归纳得 ,. ……………… 7分 当动点到达处时,运动的总路径的长为点的横纵坐标之和再减去1, 即 . ……………………………………… 8分查看更多