- 2021-05-10 发布 |
- 37.5 KB |
- 9页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
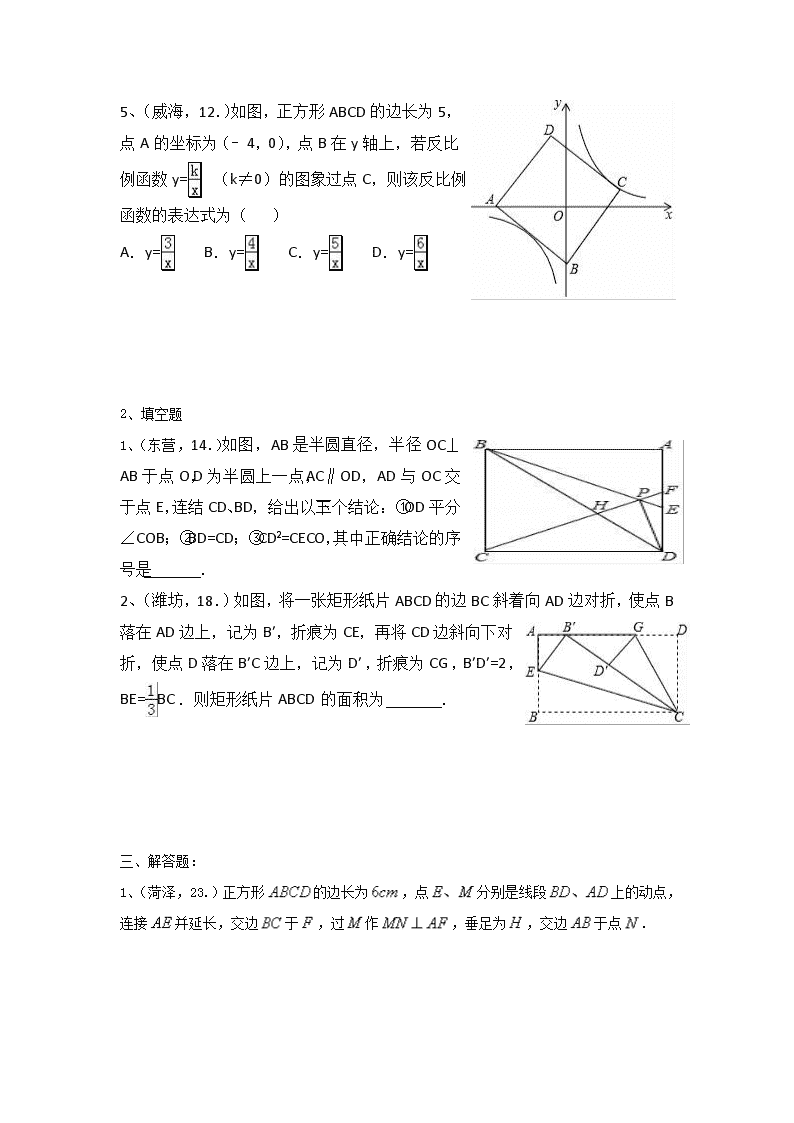
2017山东数学中考真题分类汇编几何综合大题
2017山东数学中考真命题分类会哦变——几何综合大题 一、 选择题: 1、(德州,11.)如图放置的两个正方形,大正方形ABCD边长为a,小正方形CEFG边长为b(a>b),M在BC边上,且BM=b,连接AM,MF,MF交CG于点P,将△ABM绕点A旋转至△ADN,将△MEF绕点F旋转至△NGF,给出以下五个结论:①∠MAD=∠AND;②CP=b﹣;③△ABM≌△NGF;④S四边形AMFN=a2+b2;⑤A,M,P,D四点共圆,其中正确的个数是( ) A.2 B.3 C.4 D.5 2、(东营,10.)如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连接BD、DP,BD与CF相交于点H,给出下列结论: ①BE=2AE;②△DFP∽△BPH;③△PFD∽△PDB;④DP2=PHPC 其中正确的是( ) A.①②③④ B.②③ C.①②④ D.①③④ 3、(泰安,19.)如图,四边形ABCD是平行四边形,点E是边CD上一点,且BC=EC,CF⊥BE交AB于点F,P是EB延长线上一点,下列结论: ①BE平分∠CBF;②CF平分∠DCB;③BC=FB;④PF=PC,[来#%源:^~中教网&]其中正确结论的个数为( ) [来@源%:中~教网#^]A.1 B.2 C.3 D.4 4、(威海,10.)如图,在▱ABCD中,∠DAB的平分线交CD于点E,交BC的延长线于点G,∠ABC的平分线交CD于点F,交AD的延长线于点H,AG与BH交于点O,连接BE,下列结论错误的是( ) A.BO=OH B.DF=CE C.DH=CG D.AB=AE 5、(威海,12.)如图,正方形ABCD的边长为5,点A的坐标为(﹣4,0),点B在y轴上,若反比例函数y=(k≠0)的图象过点C,则该反比例函数的表达式为( ) A.y= B.y= C.y= D.y= 2、 填空题 1、(东营,14.)如图,AB是半圆直径,半径OC⊥AB于点O,D为半圆上一点,AC∥OD,AD与OC交于点E,连结CD、BD,给出以下三个结论:①OD平分∠COB;②BD=CD;③CD2=CECO,其中正确结论的序号是 . 2、(潍坊,18.)如图,将一张矩形纸片ABCD的边BC斜着向AD边对折,使点B落在AD边上,记为B′,折痕为CE,再将CD边斜向下对折,使点D落在B′C边上,记为D′,折痕为CG,B′D′=2,BE=BC.则矩形纸片ABCD的面积为 . 三、解答题: 1、(菏泽,23.)正方形的边长为,点分别是线段上的动点,连接并延长,交边于,过作,垂足为,交边于点. (1)如图1,若点与点重合,求证:; (2)如图2,若点从点出发,以的速度沿向点运动,同时点从点出发,以的速度沿向点运动,运动时间为. ①设,求关于t的函数表达式; ②当时,连接,求的长. 2、(德州,23.)如图1,在矩形纸片ABCD中,AB=3cm,AD=5cm,折叠纸片使B点落在边AD上的E处,折痕为PQ,过点E作EF∥AB交PQ于F,连接BF. (1)求证:四边形BFEP为菱形; (2)当点E在AD边上移动时,折痕的端点P、Q也随之移动; ①当点Q与点C重合时(如图2),求菱形BFEP的边长; ②若限定P、Q分别在边BA、BC上移动,求出点E在边AD上移动的最大距离. 3、(临沂,25.(11分))数学课上,张老师出示了问题:如图1,AC,BD是四边形ABCD的对角线,若∠ACB=∠ACD=∠ABD=∠ADB=60°,则线段BC,CD,AC三者之间有何等量关系?[中国&%@教育^出版~网] 经过思考,小明展示了一种正确的思路:如图2,延长CB到E,使BE=CD,连接AE,证得△ABE≌△ADC,从而容易证明△ACE是等边三角形,故AC=CE,所以AC=BC+CD. 小亮展示了另一种正确的思路:如图3,将△ABC绕着点A逆时针旋转60°,使AB与AD重合,从而容易证明△ACF是等边三角形,故AC=CF,所以AC=BC+CD. 在此基础上,同学们作了进一步的研究: (1)小颖提出:如图4,如果把“∠ACB=∠ACD=∠ABD=∠ADB=60°”改为“∠ACB=∠ACD=∠ABD=∠ADB=45°”,其它条件不变,那么线段BC,CD,AC三者之间有何等量关系?针对小颖提出的问题,请你写出结论,并给出证明. (2)小华提出:如图5,如果把“∠ACB=∠ACD=∠ABD=∠ADB=60°”改为“∠ACB=∠ACD=∠ABD=∠ADB=α”,其它条件不变,那么线段BC,CD,AC三者之间有何等量关系?针对小华提出的问题,请你写出结论,不用证明. 4、(青岛,24.)(本小题满分12分) [来源:中国#%&教育出*@版网] 已知:Rt△EFP和矩形ABCD如图①摆放(点P与点B重合),点F,B(P),C在同一条直线上,AB=EF=6cm,BC=FP=8cm,∠EFP=90°。如图②,△EFP从图①的位置出发,沿BC方向匀速运动,速度为1cm/s;EP与AB交于点G.同时,点Q从点C出发,沿CD方向匀速运动,速度为1cm/s。过Q作QM⊥BD,垂足为H,交AD于M,连接AF,PQ,当点Q停止运动时,△EFP也停止运动.设运动时间为t(s)(0<t<6),解答下列问题: (1)当 t 为何值时,PQ∥BD? (2)设五边形 AFPQM 的面积为 y(cm2),求 y 与 t 之间的函数关系式; (3)在运动过程中,是否存在某一时刻 t,使? 若存在,求出 t 的值;若不存在,请说明理由; (4) 在运动过程中,是否存在某一时刻 t,使点M在PG的垂直平分线上? 若存在,求出 t 的值;若不存在,请说明理由. 5、(日照,21.)阅读材料: 在平面直角坐标系xOy中,点P(x0,y0)到直线Ax+By+C=0的距离公式为:d=. 例如:求点P0(0,0)到直线4x+3y﹣3=0的距离. 解:由直线4x+3y﹣3=0知,A=4,B=3,C=﹣3, ∴点P0(0,0)到直线4x+3y﹣3=0的距离为d==. 根据以上材料,解决下列问题: 问题1:点P1(3,4)到直线y=﹣x+的距离为 ; 问题2:已知:⊙C是以点C(2,1)为圆心,1为半径的圆,⊙C与直线y=﹣x+b相切,求实数b的值; 问题3:如图,设点P为问题2中⊙C上的任意一点,点A,B为直线3x+4y+5=0上的两点,且AB=2,请求出S△ABP的最大值和最小值. [中国^教&育*出@版~网] 6、(威海,24.) 如图,四边形ABCD为一个矩形纸片,AB=3,BC=2,动点P自D点出发沿DC方向运动至C点后停止,△ADP以直线AP为轴翻折,点D落在点D1的位置,设DP=x,△AD1P与原纸片重叠部分的面积为y. (1)当x为何值时,直线AD1过点C? (2)当x为何值时,直线AD1过BC的中点E? (3)求出y与x的函数表达式. 7、(潍坊,24.)边长为6的等边△ABC中,点D、E分别在AC、BC边上,DE∥AB,EC=2[来*源%:z#zstep&.co^m] (1)如图1,将△DEC沿射线方向平移,得到△D′E′C′,边D′E′与AC的交点为M,边C′D′与∠ACC′的角平分线交于点N,当CC′多大时,四边形MCND′为菱形?并说明理由. (2)如图2,将△DEC绕点C旋转∠α(0°<α<360°),得到△D′E′C,连接AD′、BE′.边D′E′的中点为P. ①在旋转过程中,AD′和BE′有怎样的数量关系?并说明理由; ②连接AP,当AP最大时,求AD′的值.(结果保留根号) [来~%#源:*&中教网] 8、(烟台23.(10分))【操作发现】 (1)如图1,△ABC为等边三角形,现将三角板中的60°角与∠ACB重合,再将三角板绕点C按顺时针方向旋转(旋转角大于0°且小于30°),旋转后三角板的一直角边与AB交于点D,在三角板斜边上取一点F,使CF=CD,线段AB上取点E,使∠DCE=30°,连接AF,EF. ①求∠EAF的度数; ②DE与EF相等吗?请说明理由; 【类比探究】 (2)如图2,△ABC为等腰直角三角形,∠ACB=90°,先将三角板的90°角与∠ACB重合,再将三角板绕点C按顺时针方向旋转(旋转角大于0°且小于45°),旋转后三角板的一直角边与AB交于点D,在三角板另一直角边上取一点F,使CF=CD,线段AB上取点E,使∠DCE=45°,连接AF,EF,请直接写出探究结果: ①求∠EAF的度数; ②线段AE,ED,DB之间的数量关系. 9、(淄博23.)如图,将矩形纸片ABCD沿直线MN折叠,顶点B恰好与CD边上的动点P重合(点P不与点C,D重合),折痕为MN,点M,N分别在边AD,BC上,连接MB,MP,BP,BP与MN相交于点F. (1)求证:△BFN∽△BCP; (2)①在图2中,作出经过M,D,P三点的⊙O(要求保留作图痕迹,不写作法); ②设AB=4,随着点P在CD上的运动,若①中的⊙O恰好与BM,BC同时相切,求此时DP的长. (图1) (图2) (图3) (第23题图) [来^源~:中&#教网%] [来@源:zzstep%.com&#^] (2014•广州10.(3分))如图,四边形ABCD、CEFG都是正方形,点G在线段CD上,连接BG、DE,DE和FG相交于点O,设AB=a,CG=b(a>b).下列结论:①△BCG≌△DCE;②BG⊥DE;③=;④(a﹣b)2•S△EFO=b2•S△DGO.其中结论正确的个数是( ) A. 4个 B. 3个 C. 2个 D. 1个 考点: 相似三角形的判定与性质;全等三角形的判定与性质;正方形的性质. 分析: 由四边形ABCD和四边形CEFG是正方形,根据正方形的性质,即可得BC=DC,CG=CE,∠BCD=∠ECG=90°,则可根据SAS证得①△BCG≌△DCE;然后根据全等三角形的对应角相等,求得∠CDE+∠DGH=90°,则可得②BH⊥DE.由△DGF与△DCE相似即可判定③错误,由△GOD与△FOE相似即可求得④. 解答: 证明:①∵四边形ABCD和四边形CEFG是正方形, ∴BC=DC,CG=CE,∠BCD=∠ECG=90°, ∴∠BCG=∠DCE, 在△BCG和△DCE中, , ∴△BCG≌△DCE(SAS), ②∵△BCG≌△DCE, ∴∠CBG=∠CDE, 又∠CBG+∠BGC=90°, ∴∠CDE+∠DGH=90°, ∴∠DHG=90°, ∴BH⊥DE; ③∵四边形GCEF是正方形, ∴GF∥CE, ∴=, ∴=是错误的. ④∵DC∥EF, ∴∠GDO=∠OEF, ∵∠GOD=∠FOE, ∴△OGD∽△OFE, ∴=()2=()2=, ∴(a﹣b)2•S△EFO=b2•S△DGO.故应选B 点评: 此题考查了正方形的性质,全等三角形的判定与性质,相似三角形的判定和性质,直角三角形的判定和性质.查看更多