2011中考专题复习之函数的几何应用
一、选择题
1. (2011•安顺)正方形 ABCD 边长为 1,E、F、G、H 分别为边 AB、BC、CD、DA 上的
点,且 AE=BF=CG=DH.设小正方形 EFGH 的面积为 y,AE=x.则 y 关于 x 的函数图象大
致是( )
A、 B、
C、 D、
考点:二次函数综合题。
分析:由已知得 BE=CF=DG=AH=1﹣x,根据 y=S 正方形 ABCD﹣S△AEH﹣S△BEF﹣S△CFG﹣S△DGH,
求函数关系式,判断函数图象.
解答:解:依题意,得 y=S 正方形 ABCD﹣S△AEH﹣S△BEF﹣S△CFG﹣S△DGH
=1﹣4× (1﹣x)x=2x2﹣2x+1,
即 y=2x2﹣2x+1(0≤x≤1),
抛物线开口向上,对称轴为 x= ,
故选 C.
点评:本题考查了二次函数的综合运用.关键是根据题意,列出函数关系式,判断图形的自
变量取值范围,开口方向及对称轴.
二、填空题
1. (2011 山东日照,16,4 分)正方形 ABCD 的边长为 4,M、N 分别是 BC、CD 上的两
个动点,且始终保持 AM⊥MN.当 BM= 2 时,四边形 ABCN 的面积最大.
考点:二次函数的最值;正方形的性质;相似三角形的判定与性质。
专题:应用题。
分析:设 BM=x,则 MC=﹣4x,当 AM⊥MN 时,利用互余关系可证△ABM∽△MCN,利
用相似比求 CN,根据梯形的面积公式表示四边形 ABCN 的面积,用二次函数的性质求面积
的最大值.
解答:解:设 BM=x,则 MC=﹣4x,
∵∠AMN=90°,
∴∠AMB=90°﹣∠NMC=∠MNC,
∴△ABM∽△MCN,则
CN
BM
MC
AB ,即
CN
x
x
4
4 ,
解得 CN=
4
)4( xx ,
∴S 四边形 ABCN=
2
1 ×4×[4+
4
)4( xx ]=﹣
2
1 x2+2x+8,
∵﹣
2
1 <0,
∴当 x=
)2
1(2
2
=2 时,S 四边形 ABCN 最大.
故答案为:2.
点评:本题考查了二次函数的性质的运用.关键是根据已知条件判断相似三角形,利用相似
比求函数关系式.
三、解答题
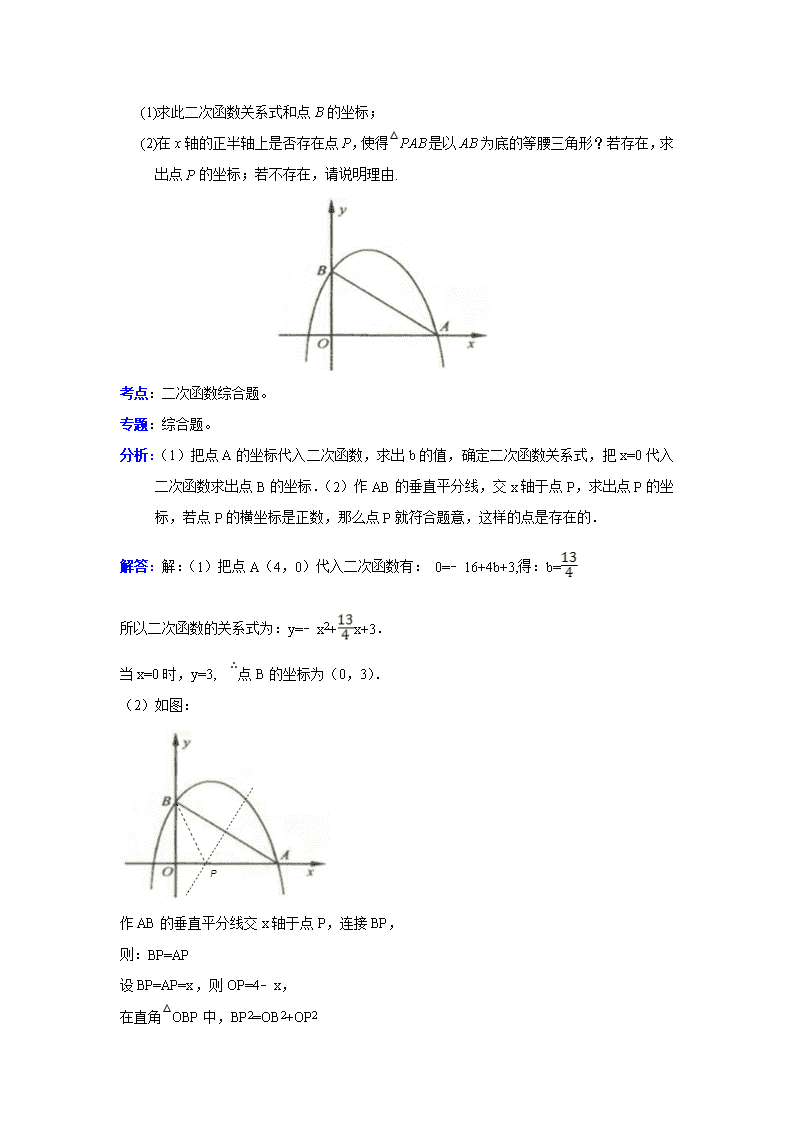
1. (2011 江苏淮安,26,10 分)如图,已知二次函数 y= -x2+bx+3 的图象与 x 轴的一个交
点为 A(4,0),与 y 轴交于点 B.
(1)求此二次函数关系式和点 B 的坐标;
(2)在 x 轴的正半轴上是否存在点 P,使得△PAB 是以 AB 为底的等腰三角形?若存在,
求出点 P 的坐标;若不存在,请说明理由.
考点:二次函数综合题。
专题:综合题。
分析:(1)把点 A 的坐标代入二次函数,求出 b 的值,确定二次函数关系式,把 x=0 代入
二次函数求出点 B 的坐标.(2)作 AB 的垂直平分线,交 x 轴于点 P,求出点 P 的坐
标,若点 P 的横坐标是正数,那么点 P 就符合题意,这样的点是存在的.
解答:解:(1)把点 A(4,0)代入二次函数有: 0=﹣16+4b+3,得:b=
所以二次函数的关系式为:y=﹣x2+ x+3.
当 x=0 时,y=3, ∴点 B 的坐标为(0,3).
(2)如图:
作 AB 的垂直平分线交 x 轴于点 P,连接 BP,
则:BP=AP
设 BP=AP=x,则 OP=4﹣x,
在直角△OBP 中,BP2=OB2+OP2
即:x2=32+(4﹣x)2, 解得:x= ,∴OP=4﹣ =
所以点 P 的坐标为:( ,0)
点评:本题考查的是二次函数的综合题,(1)根据二次函数的概念求出抛物线的解析式及点
B 的坐标.(2)根据等腰三角形的性质,利用勾股定理求出点 P 的坐标.
2. (2011 江苏淮安,28,12 分)如图,在 Rt△ABC 中,∠C=90°,AC=8,BC=6,点 P 在
AB 上,AP=2.点 E、F 同时从点 P 出发,分别沿 PA、PB 以每秒 1 个单位长度的速度向
点 A、B 匀速运动,点 E 到达点 A 后立即以原速度沿 AB 向点 B 运动,点 F 运动到点 B
时停止,点 E 也随之停止.在点 E、F 运动过程中,以 EF 为边作正方形 EFGH,使它与
△ABC 在线段 AB 的同侧,设 E、F 运动的时间为 t 秒(t>0),正方形 EFGH 与△ABC
重叠部分面积为 S.
(1)当 t=1 时,正方形 EFGH 的边长是 ;当 t=3 时,正方形 EFGH 的边长
是 ;
(2)当 0<t≤2 时,求 S 与 t 的函数关系式;
(3)直接答出:在整个运动过程中.......,当 t 为何值时,S 最大?最大面积是多少?
考点:相似三角形的判定与性质;二次函数的最值;勾股定理;正方形的性质。
专题:计算题;几何动点问题;分类讨论。
分析:(1)当时 t=1 时,可得,EP=1,PF=1,EF=2 即为正方形 EFGH 的边长;当 t=3 时,
PE=1,PF=3,即 EF=4;
(2)正方形 EFGH 与△ABC 重叠部分的形状,依次为正方形、五边形和梯形;可分
三段分别解答:①当 0<t≤ 时;②当 <t≤ 时;③当 <t≤2 时;依次求 S
与 t 的函数关系式;
(3)当 t=5 时,面积最大;
解答:解:(1)当时 t=1 时,则 PE=1,PF=1,∴正方形 EFGH 的边长是 2;当 t=3 时,PE=1,
PF=3,∴正方形 EFGH 的边长是 4;
(2):①当 0<t≤ 时, S 与 t 的函数关系式是 y=2t×2t=4t2;
②当 <t≤ 时, S 与 t 的函数关系式是: y=4t2﹣ [2t﹣ (2﹣t)]× [2t﹣ (2﹣t)] =
﹣ t2+11t﹣3;
③当 <t≤2 时; S 与 t 的函数关系式是 y= (t+2)× (t+2)﹣ (2﹣t)(2﹣t)=3t;
(3)当 t=5 时,最大面积是: S=16﹣ × × = ;
点评:本题考查了动点函数问题,其中应用到了相似形、正方形及勾股定理的性质,锻炼了
学生运用综合知识解答题目的能力.
3. (2011 江苏连云港,25,10 分)如图,抛物线 21
2y x x a 与 x 轴交于 A,B 两点,
与 y 轴交于点 C,其顶点在直线 y=-2x 上.
(1)求 a 的值;
(2)求 A,B 两点的坐标;
(3)以 AC,CB 为一组邻边作□ABCD,则点 D 关于 x 轴的对称点 D´是否在该抛物线上?请说
明理由.
考点:二次函数综合题。
分析:(1)根据二次函数的顶点坐标的求法得出顶点坐标,再代入一次函数即可求出 a 的值;
(2)根据二次函数解析式求出与 x 轴的交点坐标即是 A,B 两点的坐标;
(3)根据平行四边形的性质得出 D 点的坐标,即可得出 D′点的坐标,即可得出答案.
解答:解:(1)∵抛物线 y= x2﹣x+a 其顶点在直线 y=﹣2x 上.
∴抛物线 y= x2﹣x+a= (x2﹣2x)+a= (x﹣1)2﹣ +a,
∴顶点坐标为:(1,﹣ +a),∴y=﹣2x,﹣ +a=﹣2,∴a=﹣ ;
(2)二次函数解析式为:y= x2﹣x﹣ ,
∵抛物线 y= x2﹣x﹣ 与 x 轴交于点 A,B,∴0= x2﹣x﹣ ,整理得:x2﹣2x﹣3=0,解得:
x=﹣1 或 3, A(﹣1,0),B(3,0);
(3)作出平行四边形 ACBD,作 DE⊥AB,
∵二次函数解析式为:y= x2﹣x﹣ ,∴图象与 y 轴交点坐标为:(0,﹣ ),∴CO= ,∴DE= ,
∵∠CAO=∠DBE,∠DEB=∠AOC,∴△AOC≌△BDE,∵AO=1,∴BE=1, D 点的坐标
为:(2, ),
∴点 D 关于 x 轴的对称点 D′坐标为:(2,﹣ ),
代入解析式 y= x2﹣x﹣ ,左边=﹣ ,右边= ×4﹣2﹣ =﹣ ,∴D′点在函数图象上.
点评:此题主要考查了二次函数的综合应用以及平行四边形的性质,根据平行四边形的性质
得出 D 点的坐标是解决问题的关键.
4. (2011 江苏苏州,29,10 分)巳知二次函数 y=a(x2-6x+8)(a>0)的图象与 x 轴分别
交于点 A、B,与 y 轴交于点 C.点 D 是抛物线的顶点.
(1)如图①.连接 AC,将△OAC 沿直线 AC 翻折,若点 O 的对应点 0'恰好落在该抛物线
的 对称轴上,求实数 a 的值;
(2)如图②,在正方形 EFGH 中,点 E、F 的坐标分别是(4,4)、(4,3),边 HG 位于边
EF 的 右侧.小林同学经过探索后发现了一个正确的命题:“若点 P 是边 EH 或边 HG 上的任
意一点,则四条线段 PA、PB、PC、PD 不能与任何一个平行四边形的四条边对应相等 (即
这四条线段不能构成平行四边形).“若点 P 是边 EF 或边 FG 上的任意一点,刚才的结论是
否也成立?请你积极探索,并写出探索过程;
(3)如图②,当点 P 在抛物线对称轴上时,设点 P 的纵坐标 l 是大于 3 的常数,试问:是
否存在一个正数阿 a,使得四条线段 PA、PB、PC、PD 与一个平行四边形的四条边对应相
等 (即这四条线段能构成平行四边形)?请说明理由.
考点:二次函数综合题.
分析:(1)本题需先求出抛物线与 x 轴交点坐标和对称轴,再根据∠OAC=60°得出 AO,从
而求出 a.
(2)本题需先分两种情况进行讨论,当 P 是 EF 上任意一点时,可得 PC>PB,从而得出
PB≠PA,PB≠PC,PB≠PD,即可求出线段 PA、PB、PC、PD 不能构成平行四边形.
(3)本题需先得出 PA=PB,再由 PC=PD,列出关于 t 与 a 的方程,从而得出 a 的值,即可
求出答案.
解答:解:(1)令 y=0,由
2( 6 8) 0a x x 解得 1 22, 4x x ;
令 x=0,解得 y=8a.
∴点 A、B、C 的坐标分别是(2,0)、(4,0)、(0,8a),
该抛物线对称轴为直线 x=3.
∴OA=2.
如图①,时抛物线与 x 轴交点为 M,则 AM=1.
由题意得: 2O A OA .
∴ 2O A AM ,∴∠O’AM=60°.
∴ 3 2 3OC AO ,即8 2 3a .∴
3
4a
.
(2)若点 P 是边 EF 或边 FG 上的任意一点,结论同样成立.
(Ⅰ)如图②,设点 P 是边 EF 上的任意一点 (不与点 E 重合),连接 PM.
∵点 E(4,4)、F(4,3)与点 B(4,0)在一直线上,点 C 在 y 轴上,
∴PB<4,PC≥4,∴PC>PB.
又 PD>PM>PB,PA>PM>PB,
∴PB≠PA,PB≠PC,PB≠PD.
∴此时线段 PA、PB、PC、PD 不能构成平行四边形.
(Ⅱ)设 P 是边 FG 上的任意一点(不与点 G 重合),
∵点 F 的坐标是(4,3),点 G 的坐标是(5,3).
∴FB=3, 10GB ,∴3≤PB< 10 .
∵PC≥4,∴PC>PB.
(3)存在一个正数 a,使得线段 PA、PB、PC 能构成一个平行四边形.
如图③,∵点 A、B 时抛物线与 x 轴交点,点 P 在抛物线对称轴上,
∴PA=PB.
∴当 PC=PD 时,线段 PA、PB、PC 能构成一个平行四边形.
BA
y
O
(图②)
xD
C
E
F G
H
M
BA
y
O
(图③)
xD
C
E
F G
H
P
∵点 C 的坐标是(0,8a),点 D 的坐标是(3,-a).
点 P 的坐标是(3,t),
∴PC2=32+(t-8a) 2,PD2= (t+a) 2.
整理得 7a2-2ta+1=0,∴Δ=4t2-28.
∵t 是一个常数且 t>3,∴Δ=4t2-28>0
∴方程 7a2-2ta+1=0 有两个不相等的实数根
2 22 4 28 7
14 7
t t t ta
.
显然
2 7 07
t ta
,满足题意.
∵当 t 是一个大于 3 的常数,存在一个正数
2 7
7
t ta
,使得线段 PA、PB、PC 能
构成一个平行四边形.
点评:本题主要考查了二次函数的综合问题,在解题时要注意运用数形结合和分类讨论,把
二次函数的图象与性质和平行四边形的判定相结合是本题的关键.
5. (2011•江苏宿迁,27,12)如图,在边长为 2 的正方形 ABCD 中,P 为 AB 的中点,Q
为边 CD 上一动点,设 DQ=t(0≤t≤2),线段 PQ 的垂直平分线分别交边 AD、BC 于点 M、
N,过 Q 作 QE⊥AB 于点 E,过 M 作 MF⊥BC 于点 F.
(1)当 t≠1 时,求证:△PEQ≌△NFM;
(2)顺次连接 P、M、Q、N,设四边形 PMQN 的面积为 S,求出 S 与自变量 t 之间的函数
关系式,并求 S 的最小值.
考点:正方形的性质;二次函数的最值;全等三角形的判定与性质;线段垂直平分线的性质;
勾股定理。
专题:代数几何综合题。
分析:(1)由四边形 ABCD 是正方形得到∠A=∠B=∠D=90°,AD=AB,又由∠EQP=∠FMN,
而证得;
(2)由点 P 是边 AB 的中点,AB=2,DQ=AE=t,又由勾股定理求得 PQ,由△PEQ≌△NFM
得到 PQ 的值,又 PQ⊥MN 求得面积 S,由 t 范围得到 S 的最小值.
解答:证明:(1)∵四边形 ABCD 是正方形,
∴∠A=∠B=∠D=90°,AD=AB,
∵QE⊥AB,MF⊥BC,
∴∠AEQ=∠MFB=90°,
∴四边形 ABFM、AEQD 都是矩形,
∴MF=AB,QE=AD,MF⊥QE,
又∵PQ⊥MN,
∴∠EQP=∠FMN,
又∵∠QEP=∠MFN=90°,
∴△PEQ≌△NFM;
(2)∵点 P 是边 AB 的中点,AB=2,DQ=AE=t
∴PA=1,PE=1-t,QE=2
由勾股定理,得 PQ= 22 PEQE = 4)1( 2 t
∵△PEQ≌△NFM
∴MN=PQ= 4)1( 2 t
又∵PQ⊥MN
∴S= MNPQ
2
1 = 4)1(2
1 2 t =
2
1 t2-t+
2
5
∵0≤t≤2
∴当 t=1 时,S 最小值=2.
综上:S=
2
1 t2-t+
2
5 ,S 的最小值为 2.
点评:本题考查了正方形的性质,(1)由四边形 ABCD 是正方形得到∠A=∠B=∠D=90°,
AD=AB,又由∠EQP=∠FMN,而证得;(2)由勾股定理求得 PQ,由△PEQ≌△NFM 得到
PQ 的值,又 PQ⊥MN 求得面积 S,由 t 范围得到答案.
6.(2011•江苏徐州,28,12)如图,已知二次函数 y=x2+bx+c 的图象与 x 轴交于 A,B 两点,
与 y 轴交于点 P,顶点为 C(1,﹣2).
(1)求此函数的关系式;
(2)作点 C 关于 x 轴的对称点 D,顺次连接 A,C,B,D.若在抛物线上存在点 E,使直
线 PE 将四边形 ABCD 分成面积相等的两个四边形,求点 E 的坐标;
(3)在(2)的条件下,抛物线上是否存在一点 F,使得△PEF 是以 P 为直角顶点的直角三
角形?若存在,求出点 F 的坐标及△PEF 的面积;若不存在,请说明理由.
考点:二次函数综合题。
专题:代数几何综合题。
分析:(1)将顶点坐标 C(1,﹣2)代入 y=x2+bx+c 即可求得此二次函数的关系式;
(2)先求出直线 PM 的解析式,然后与二次函数联立即可解得点 E 的坐标;
(3)根据三角形相似的性质先求出 GP=GF,求出 F 点的坐标,进而求得△PEF 的面积.
解答:解(1)∵y=x2+bx+c 的顶点为(1,﹣2).
∴y=(x﹣1)2﹣2,y=x2﹣2x﹣1;
(2)连结 CD 交 AB 于点 M,
根据轴对称性可知 MA=MB,MC=MD,AB⊥CD,
所以四边形 ACBD 是菱形,
过点 M 的任意一条直线都把菱形 ACBD 的面积平分,
所以直线 PM 平分菱形 ACBD 的面积
因为 y= 2x 2x 1 与 y 相交于点 P(0,-1), 顶点为点 C(1,-2)
所以点 M 的坐标为(1,0)
设直线 PM 的解析式为 y=kx+b
则 1=b
0=k b
,解之得 k=1
b= 1
所以直线 PM 的解析式为 y=x-1
解方程组 2
y=x 1.
y=x 2x 1
,得 x=0
y= 1
或 x=3
y=2
所以点 E 的坐标为(3,2).
(3)过点 P 作直线 PQ⊥PM,则直线 PQ 的表达式为 y=-x-1
解方程组 2
y= x 1.
y=x 2x 1
,得 x=0
y= 1
或 x=1
y= 2
所以直线 PQ 与抛物线的交点 F 是抛物线的顶点 C(1,-2).
所以 PE= 2 2(3 0) (2 1) 3 3 ,PC= 2 2(1 0) ( 2 1) 2
所以△PEF 的面积为 1 33 3 2= 62 2
点评:本题是二次函数的综合题,其中涉及的到的知识点有抛物线的公式的求法及三角形的
相似等知识点,是各地中考的热点和难点,解题时注意数形结合等数学思想的运用,同学们
要加强训练,属于中档题.
7. (2011 南昌,25,10 分)如图所示,抛物线 m:y=ax2+b(a<0,b>0)与 x 轴于点 A、
B(点 A 在点 B 的左侧),与 y 轴交于点 C.将抛物线 m 绕点 B 旋转 180°,得到新的抛
物线 n,它的顶点为 C1,与 x 轴的另一个交点为 A1.
(1)当 a=﹣1,b=1 时,求抛物线 n 的解析式;
(2)四边形 AC1A1C 是什么特殊四边形,请写出结果并说明理由;
(3)若四边形 AC1A1C 为矩形,请求出 a,b 应满足的关系式.
考点:二次函数综合题.
专题:代数几何综合题.
分析:(1)根据 a=﹣1,b=1 得出抛物线 m 的解析式,再利用 C 与 C1 关于点 B 中心对
称,得出二次函数的顶点坐标,即可得出答案;
(2)利用两组对边分别相等的四边形是平行四边形即可证明;
(3)利用矩形性质得出要使平行四边形 AC1A1C 是矩形,必须满足 AB=BC,即可求出.
解答:解:(1)当 a=﹣1,b=1 时,抛物线 m 的解析式为:y=﹣x2+1.
令 x=0,得:y=1.∴C(0,1).令 y=0,得:x=±1.∴A(﹣1,0),B(1,0),
∵C 与 C1 关于点 B 中心对称,∴抛物线 n 的解析式为:y=(x﹣2)2﹣1=x2﹣4x+3;
(2)四边形 AC1A1C 是平行四边形.
理由:∵C 与 C1、A 与 A1 都关于点 B 中心对称,∴AB=BA1,BC=BC1,∴四边形 AC1A1C
是平行四边形.
(3)令 x=0,得:y=b.∴C(0,b).令 y=0,得:ax2+b=0,∴
a
by ,∴
0,
a
bA ,
0,
a
bB ,
a
bAB 2 ,
a
bbOBOCBC 222 .要使平行四边形 AC1A1C
是矩形,必须满足 AB=BC,∴
a
bba
b 22 ,∴
a
bba
b
24 ,∴ab=-3.∴a、
b 应满足关系式 ab=-3.
点评:此题主要考查了平行四边形的性质以及矩形的性质和点的坐标关于一点中心对称的性
质,灵活应用平行四边形的性质是解决问题的关键.
8. (2011 内蒙古呼和浩特,25,12)已知抛物线 y1=x2+4x+1 的图象向上平移 m 个单位(m
>0)得到的新抛物线过点(1,8).
(1)求 m 的值,并将平移后的抛物线解析式写成 y2=a(x-h)2+k 的形式;
(2)将平移后的抛物线在 x 轴下方的部分沿 x 轴翻折到 x 轴上方,与平移后的抛物线没有
变化的部分构成一个新的图象.请写出这个图象对应的函数 y 的解析式,并在所给的平面直
角坐标系中直接画出简图,同时写出该函数在-3<x≤ 3
2
时对应的函数值 y 的取值范围;
(3)设一次函数 y3=nx+3(n≠0),问是否存在正整数 n 使得(2)中函数的函数值 y=y3 时,
对应的 x 的值为-1<x<0,若存在,求出 n 的值;若不存在,说明理由.
考点:二次函数综合题.
分 析 :( 1 ) 根 据 抛 物 线 y1=x2+4x+1 的 图 象 向 上 平 移 m 个 单 位 , 可 得
y2=x2+4x+1+m,再利用又点(1,8)在图象上,求出 m 即可;
(2)根据函数解析式画出图象,即可得出函数大小分界点;
(3)根据当 y=y3 且对应的-1<x<0 时,x2+4x+3=nx+3,得出 n 取值范围即可
得出答案.
解答:解:(1)由题意可得 y2=x2+4x+1+m,
又点(1,8)在图象上,
∴8=1+4×1+1+m,
∴m=2,
∴y2=(x+2)2-1;
(2)当 3<x≤ 3
2
时,0<y≤-1;
(3)不存在,
理由:当 y=y3 且对应的-1<x<0 时,x2+4x+3=nx+3,
∴x1=0,x2=n-4,
且-1<n-4<0 得 3<n<4,
∴不存在正整数 n 满足条件.
点评:此题主要考查了二次函数的综合应用以及图象交点求法,二次函数的综合应用是初中
阶段的重点题型特别注意利用数形结合是这部分考查的重点也是难点同学们应重点掌握.
9.(2011•宁夏,26,10 分)在等腰△ABC 中,AB=AC=5,BC=6.动点 M、N 分别在两腰
AB、AC 上(M 不与 A、B 重合,N 不与 A、C 重合),且 MN∥BC.将△AMN 沿 MN 所
在的直线折叠,使点 A 的对应点为 P.
(1)当 MN 为何值时,点 P 恰好落在 BC 上?
(2)当 MN=x,△MNP 与等腰△ABC 重叠部分的面积为 y,试写出 y 与 x 的函数关系式.当
x 为何值时,y 的值最大,最大值是多少?
考点:翻折变换(折叠问题);二次函数的最值;等腰三角形的性质;相似三角形的判定与
性质。
分析:(1)首先连接 AP,交 MN 于 O,由 MN∥BC.将△AMN 沿 MN 所在的直线折叠,
使点 A 的对应点为 P,即可得△AMN∽△ABC,
2
1
AP
AO
BC
MN ,则可求得当 MN 为何值
时,点 P 恰好落在 BC 上;
(2)此题需要分为当 AO≤
2
1 AD 时与当 AO>
2
1 AD 时去分析,首先由△AMN∽△ABC,
求得各线段的长,然后求△MNP 与等腰△ABC 重叠部分的面积,即可得关于 x 的二次函数,
根据二次函数求最值的方法,即可求得答案.
解答:解:(1)连接 AP,交 MN 于 O,
∵将△AMN 沿 MN 所在的直线折叠,使点 A 的对应点为 P,
∴OA=OP,AP⊥MN,AN=PN,AM=PM,
∵MN∥BC,
∴△AMN∽△ABC,AO⊥MN,
∴
2
1
AP
AO
BC
MN ,
∵BC=6,
∴MN=3,
∴当 MN=3 时,点 P 恰好落在 BC 上;
(3)过点 A 作 AD⊥BC 于 D,交 MN 于 O,
∵MN∥BC,
∴AO⊥MN,
∴△AMN∽△ABC,
∴
AD
AO
BC
MN ,
∵AB=AC=5,BC=6,AD⊥BC,
∴∠ADB=90°,BD=
2
1 BC=3,
∴AD=4,
∴
46
AOx ,
∴AO=
3
2 x,
∴S△AMN=
2
1 MN•AO=
2
1 •x•
3
2 x=
3
1 x2,
当 AO≤
2
1 AD 时,
根据题意得:S△PMN=S△AMN,
∴△MNP 与等腰△ABC 重叠部分的面积为 S△AMN,
∴y=
3
1 x2,
∴当 AO=
2
1 AD 时,即 MN=
2
1 BC=3 时,y 最小,最小值为 3;
当 AO>
2
1 AD 时,
连接 AP 交 MN 于 O,
则 AO⊥MN,
∵MN∥BC,
∴AP⊥BC,△AMN∽△ABC,△PEF∽△PMN∽△AMN,
∴
AD
AO
BC
MN ,
PO
PD
MN
EF ,
即:
46
AOx ,
AO
PD
x
EF ,
∴AO=
3
2 x,
∴
AO
ADAO
x
EF 2 ,
∴EF=2x﹣6,OD=AD﹣AO=4﹣
3
2 x,
∴y=S 梯形 MNFE=
2
1 (EF+MN)•OD=
2
1 ×(2x﹣6+x)×(4﹣
3
2 x)=﹣(x﹣4)2+4,
∴当 x=4 时,y 有最大值,最大值为 4,
综上所述:当 x=4 时,y 的值最大,最大值是 4.
点评:此题考查了相似三角形的判定与性质,二次函数的最值问题等知识.解题的关键是方
程思想、分类讨论思想与数形结合思想的应用.
10. (2011 山东日照,24,10 分)如图,抛物线 y=ax2+bx(a>0)与双曲线 y=
x
k 相交于点
A,B.已知点 B 的坐标为(﹣2,﹣2),点 A 在第一象限内,且 tan∠AOx=4.过点 A 作直
线 AC∥x 轴,交抛物线于另一点 C.
(1)求双曲线和抛物线的解析式;
(2)计算△ABC 的面积;
(3)在抛物线上是否存在点 D,使△ABD 的面积等于△ABC 的面积.若存在,请你写出
点 D 的坐标;若不存在,请你说明理由.
考点:二次函数综合题。
专题:代数几何综合题。
分析:(1)根据已知条件可以推出 A 点的坐标,把 A、B 两点的坐标代入抛物线解析式和
双曲线解析式,即可得出 a、b、k 的值,就可以确定双曲线和抛物线的解析式了;
(2)根据 A、B 抛物线解析式,可以确定 C 点的坐标,即可去顶 AC 和 AC 边上的高的长
度,就可以计算出△ABC 的面积了;
(3)根据题意画出图形,根据 A、B 两点坐标出去直线 AB 相应的一次函数结合 C 点的坐
标,CD∥AB,得出直线 CD 相应的一次函数,然后结合 D 点也在抛物线上,解方程组,求
D 点坐标
解答:解:(1)把点 B(﹣2,﹣2)的坐标,代入 y=
x
k ,
得:﹣2=
2
k ,∴k=4.
即双曲线的解析式为:y=
x
4 .(2 分)
设 A 点的坐标为(m,n).∵A 点在双曲线上,∴mn=4.①
又∵tan∠AOx=4,∴
n
m =4,即 m=4n.②
又①,②,得:n2=1,∴n=±1.
∵A 点在第一象限,∴n=1,m=4,∴A 点的坐标为(1,4)
把 A、B 点的坐标代入 y=ax2+bx,得:
ba
ba
242
4 解得 a=1,b=3;
∴抛物线的解析式为:y=x2+3x;(4 分)
(2)∵AC∥x 轴,∴点 C 的纵坐标 y=4,
代入 y=x2+3x,得方程 x2+3x﹣4=0,解得 x1=﹣4,x2=1(舍去).
∴C 点的坐标为(﹣4,4),且 AC=5,(6 分)
又△ABC 的高为 6,∴△ABC 的面积=
2
1 ×5×6=15;(7 分)
(3)存在 D 点使△ABD 的面积等于△ABC 的面积.
过点 C 作 CD∥AB 交抛物线于另一点 D.
因为直线 AB 相应的一次函数是:y=2x+2,且 C 点的坐标为(﹣4,4),CD∥AB,
所以直线 CD 相应的一次函数是:y=2x+12.(9 分)
解方程组
122
32
xy
xxy 得
18
3
y
x 所以点 D 的坐标是(3,18)(10 分)
点评:本题是二次函数的综合题型,其中涉及的到大知识点根据点的坐标求抛物线解析式和
双曲线解析式以及三角形的面积求法.关键在于根据点的坐标和相关的知识点求抛物线解析
式,曲线解析式和直线解析式.
11. (2011 山西,26,14 分)如图,在平面直角坐标系中,四边形 OABC 是平行四边形,
直线 l 经过 O、C 两点,点 A 的坐标为(8,0),点 B 的坐标为(11,4),动点 P 在
线段 OA 上从点 O 出发以每秒 1 个单位的速度向点 A 运动,同时动点 Q 从点 A 出发以
每秒 2 个单位的速度沿 A B C 的方向向点 C 运动,过点 P 作 PM 垂直于 x 轴,与折
线 O—C—B 相交于点 M,当 P、Q 两点中有一点到达终点时,另一点也随之停止运动,
设点 P、Q 运动的时间为 t 秒(t > 0),△MPQ 的面积为 S.
(1)点 C 的坐标为____________,直线 l 的解析式为_____________;
(2)试求点 Q 与点 M 相遇前 S 与 t 的函数关系式,并写出相应的 t 的取值范围.
(3)试求题(2)中当 t 为何值时,S 的值最大,并求出 S 的最大值.
(4)随着 P、Q 两点的运动,当点 M 在线段 BC 上运动时,设 PM 的延长线与直线 l
相交于点 N.试探究:当 t 为何值时,△QMN 为等腰三角形?请直接写出 t 的值.
考点:二次函数,一次函数,三角形面积,最值,分类讨论
专题:压轴题
分析:⑴由题意不难得出点 C 的坐标为(3,4).因为直线 l 经过 O、C 两点,所以设其
解析式为 y kx ,将点 C(3,4)代入,解得 4
3k ,所以直线 l 的解析式为 4
3y x .
⑵求 S 与 t 的函数关系式,关键是确定 MP 及点 Q 到 MP 的距离.根据题意,得 OP=
t, AQ=2t, 根据动点的运动过程,需分三种情况来讨论.
1 当 0<t≤ 5
2
时; 如图第 26 题(2)图 1,由题意可证△AEQ∽△ODC,得 6
5
tAE ,
8
5EQ t .∴Q 点的坐标是( 68 5
t , 8
5
t ).∴ 6 18 85 5PE t t t .
∴ 21 1 4 1 2 1682 2 3 5 15 3S MP PE t t t t
.
②当 5
2
<t≤3 时; 如图第 26 题(2)图 2,∵BQ=2t-5,∴OF=11-(2t-5)=16-2t.
∴Q 点的坐标是(16-2t,4).∴PF=16-2t-t=16-3t.
∴ 21 1 4 3216 3 22 2 3 3S MP PF t t t t .
③当 3<t<16
3
时,如图第 26 题(2)图 3,当点 Q 与点 M 相遇时,16-2t=t,解得 16
3t .
当 3<t<16
3
时,如图 3,MQ=16-2t-t=16-3t,MP=4.
∴ 1 1 4 16 3 6 322 2S MP MQ t t
⑶根据题(2)中 S 与 t 的函数关系,先分别求出①当 0<t≤ 5
2
时;②当 5
2
<t≤3 时;③
当 3<t<16
3
时, t 为何值时,S 的值最大,并求出 S 的最大值.最后综合上述各情况判断
得出 t 为何值时, S 的最大值.
①当 0<t≤ 5
2
时, 222 16 2 1602015 3 15 3S t t t .
∵a= 2
15
>0,抛物线开口向上,对称轴为直线 x=-20,
∴当 0<t≤ 5
2
时,S 随 t 的增大而增大.
∴当 t= 5
2
时,S 有最大值,最大值为 85
6
.
②当 5
2
<t≤3 时,
2
2 32 8 1282 23 3 9S t t t
.
∵a=-2<0.抛物线开口向下,
∴当 8
3t 时,S 有最大值,最大值为128
9
.
③当 3<t<16
3
时, 6 32S t ,∵k=-6<0,∴S 随 t 的增大而减小.
又∵当 t=3 时,S=14.当 t=16
3
时,S=0,∴0<S<14.
综上所述,当 8
3t 时,S 有最大值,最大值为128
9
.
⑷如图第 26 图(4),当 NM=MQ 时,即 416 3 43t t ,△QMN 为等腰三角形.
解答:(1)(3,4); xy 3
4 .
(2)根据题意,得 OP= t,AQ=2 t,分三种情况讨论:
①当 0
0 时,抛物线开口向上,对称轴为直线 t =-20,
当 0< t ≤
2
5 时,S 随 t 的增大而增大,∴当 t=
2
5 时,S 有最大值.最大值为
6
85 .
②当
2
5 < t≤3 时,
9
128
3
8-t2-3
322-
2
2
ttS ,∵a=-2<0,抛物线开口向下,
∴当 t=
3
8 时,S 有最大值,最大值为
9
128 .
③当 3< t <
3
16 时,S = -6t+32,∵k=-6<0,∴S 随着 t 的增大而减小,又∵当 t=3
时,S=14,当 t=
3
16 时,S=0,所以 00,a 为常数),并经过点(2a,2a),点 D(0,2a)为一定
点.
(1)求含有常数 a 的抛物线的解析式;
(2)设点 P 是抛物线任意一点,过 P 作 PH⊥x 轴,垂足是 H,求证:PD = PH;
(3)设过原点 O 的直线 l 与抛物线在第一象限相交于 A、B 两点,若 DA=2DB,且 S△ABD = 4 2,
求 a 的值.
考点:二次函数综合题.
分析:(1)根据抛物线的图象假设出解析式为 y=kx2+a,将经过点(2a,2a),代入求出即可;
(2)根据勾股定理得出 PD2=DG2+PG2,进而求出 PD=PH;
(3)利用(2)中结论得出 BE=DB,AF=DA,即可得出 B 是 OA 的中点,进而得出 S△OBD=S△ABD=4
,即可得出 a 的值.
答案:24.解:(1)设抛物线的解析式为 y=kx2+a
∵点 D(2a,2a)在抛物线上,
4a2k+a = 2a ∴k = 1
4a
(24 题图)
(24 题图)
∴抛物线的解析式为 y= 1
4a
x2+a
(2)设抛物线上一点 P(x,y),过 P 作 PH⊥x 轴,PG⊥y 轴,在 Rt△GDP 中,
由勾股定理得:PD2=DG2+PG2=(y–2a)2+x2 =y2 – 4ay+4a2+x2
∵y= 1
4a
x2+a ∴x2 = 4a (y– a)= 4ay– 4a2
∴PD 2= y2– 4ay+4a2 +4ay– 4a2= y2 =PH2
∴PD = PH
(3)过 B 点 BE ⊥ x 轴,AF⊥x 轴.
由(2)的结论:BE=DB AF=DA
∵DA=2DB ∴AF=2BE ∴AO = 2BO
∴B 是 OA 的中点,
∴C 是 OD 的中点,
连结 BC
∴BC= DA
2
= AF
2
= BE = DB
过 B 作 BR⊥y 轴,
∵BR⊥CD ∴CR=DR,OR= a + a
2
= 3a
2
,
∴B 点的纵坐标是3a
2
,又点 B 在抛物线上,
∴3a
2
= 1
4a
x2+a ∴x2 =2a2
∵x>0 ∴x = 2a
∴B ( 2a,3a
2
)
AO = 2OB, ∴S△ABD=S△OBD = 4 2
所以,1
22a 2a= 4 2
∴a2= 4 ∵a>0 ∴a = 2
点评:此题主要考查了二次函数的综合应用以及勾股定理的应用,二次函数的综合应用是初
中阶段的重点题型特别注意利用数形结合是这部分考查的重点也是难点同学们应重点掌握.
44. (2011 四川雅安,25,12 分)如图,已知二次函数 y=ax2+2x+c(a>0)图象的顶点 M 在
反比例函数 3y x
上,且与 x 轴交于 AB 两点.
(1)若二次函数的对称轴为 1
2x ,试求 a,c 的值;
(2)在(1)的条件下求 AB 的长;
(3)若二次函数的对称轴与 x 轴的交点为 N,当 NO+MN 取最小值时,试求二次函数的解
析式.
考点:二次函数综合题。
分析:(1)根据对称轴 x=﹣
2
b
a
= 1
2
,求得二次函数 y=ax2+2x+c(a>0)中的 a,再
根据顶点在反比例函数 3y x
上,求出 c 即可;
(2)求得抛物线与 x 轴的交点坐标,再用点 B 的横坐标减去点 A 的横坐标即可.
(3)可用含有 a 的式子表示点 M、N 的坐标,即求出 a 的值,再求得解析式.
解答:解:(1)∵二次函数的对称轴为 1
2x ,
∴﹣
2
b
a
=﹣ 1
2
,
解得 a=2,
∵二次函数 y=ax2+2x+c(a>0)图象的顶点 M 在反比例函数 3y x
上,
∴顶点为( 1
2
,c 1
2
),
∴ 1
2
(c 1
2
)=﹣3,
解得 c=﹣11
2
,
∴二次函数的解析式为 y=2x2+2x﹣ 11
2
;
(2)∵二次函数的解析式为 y=2x2+2x﹣11
2
;
∴令 y=0,2x2+2x﹣11
2
=0;
解得 x= 1 2 3
2
.
∴AB= 1 2 3
2
1 2 3
2
=2 3 ;
(3)根据对称轴 x=﹣ 1
a
,当 x=﹣ 1
a
时,y=﹣3a,
∴NO+MN= 1
a
+3a=
23 1a
a
,
要使 NO+MN 最小,则 3a2+1 最小即可,
即 3a2=1 时,a= 3
3
,
∴此时二次函数的解析式为 y= 3
3
x2+2x+3 3 .
点评:本题是二次函数的综合题,其中涉及到的知识点有最值问题和两点之间的距离等知识
点,是各地中考的热点和难点,解题时注意数形结合等数学思想的运用,同学们要加强训练,
属于中档题.
45. 如图,抛物线与 x 轴交于 A( 1x ,0)、B( 2x ,0)两点,且 1 2x x ,与 y 轴交于点 0, 4C ,
其中 1 2x x, 是方程 2 4 12 0x x 的两个根.
(1)求抛物线的解析式;
(2)点 M 是线段 AB 上的一个动点,过点 M 作 MN ∥ BC ,交 AC 于点 N ,连接CM ,
当 CMN△ 的面积最大时,求点 M 的坐标;
(3)点 4,D k 在(1)中抛物线上,点 E 为抛物线上一动点,在 x 轴上是否存在点 F ,
使以 A D E F、 、 、 为顶点的四边形是平行四边形,如果存在,求出所有满足条件的点 F 的
坐标,若不存在,请说明理由.
考点:二次函数综合题.
分析:(1)根据一元二次方程解法得出 A,B 两点的坐标,再利用交点式求出二次函数解析
式;
(2)首先判定△MNA∽△ABC.得出
AB
AM
CO
NH ,进而得出函数的最值;
(3)分别根据当 AF 为平行四边形的边时,AF 平行且等于 DE 与当 AF 为平行四边形
的对角线时,分析得出符合要求的答案.
解答:解:(1)∵ 2 4 12 0x x ,∴ 1 2x , 2 6x . ∴ ( 2,0)A , (6,0)B .
又∵抛物线过点 A 、 B 、C ,故设抛物线的解析式为 ( 2)( 6)y a x x ,
将点C 的坐标代入,求得 1
3a 。
y
x
O
B
M
N
C
A
28 题图
∴抛物线的解析式为 21 4 43 3y x x .
(2)设点 M 的坐标为( m ,0),过点 N 作 NH x 轴于点 H (如图(1))。
∵点 A 的坐标为( 2 ,0),点 B 的坐标为(6,0),
∴ 8AB , 2AM m .
∵MN∥BC,∴△AMN∽△ABC .
∴ NH AM
CO AB
,∴ 2
4 8
NH m ,∴ 2
2
mNH .
∴ NHAMCOAMSSS AMNACMACM
2
1
2
1
△△△
21 2 1( 2)(4 ) 32 2 4
mm m m .
21 ( 2) 44 m 。
∴当 2m 时, CMNS△ 有最大值 4。
此时,点 M 的坐标为(2,0).
(3)∵点 D (4, k )在抛物线 21 4 43 3y x x 上,
∴当 4x 时, 4k ,
∴点 D 的坐标是(4, 4 )。
①如图(2),当 AF 为平行四边形的边时, AF DE ,
∵ D (4, 4 ),∴ 4DE .
∴ 1( 6,0)F , 2 (2,0)F .
②如图(3),当 AF 为平行四边形的对角线时,设 ( ,0)F n ,
则平行四边形的对称中心为( 2
2
n ,0).
∴ E 的坐标为( 6n ,4)。
把 E
( 6n ,4)代入 21 4 43 3y x x ,得 2 16 36 0n n .
解得 8 2 7n .
3 (8 2 7,0)F , 4 (8 2 7,0)F .
点评:此题主要考查了二次函数的综合应用,二次函数的综合应用是初中阶段的重点题型特
别注意利用数形结合是这部分考查的重点也是难点同学们应重点掌握.
46.(2011 四川眉山,26,11 分)如图,在直角坐标系中,已知点 A(0,1),B(﹣4,4),
y
x
O
B
M
N
C
A
图(1)
H
y
x
O
B
2F
E
A
图(2)
1F
D
y
xO B
3F
E
A
图(3)
E
D
4F
E
将点 B 绕点 A 顺时针方向 90°得到点 C;顶点在坐标原点的拋物线经过点 B.
(1)求抛物线的解析式和点 C 的坐标;
(2)抛物线上一动点 P,设点 P 到 x 轴的距离为 d1,点 P 到点 A 的距离为 d2,试说明 d2=d1+1;
(3)在(2)的条件下,请探究当点 P 位于何处时,△PAC 的周长有最小值,并求出△PAC
的周长的最小值.
考点:二次函数综合题。
专题:综合题。
分析:(1)设抛物线的解析式:y=ax2,把 B(﹣4,4)代入即可得到 a 的值;过点 B 作 BE⊥y
轴于 E,过点 C 作 CD⊥y 轴于 D,易证 Rt△BAE≌Rt△ACD,得到 AD=BE=4,CD=AE=OE
﹣OA=4﹣1=3,即可得到 C 点坐标(3,5);
(2)设 P 点坐标为(a,b),过 P 作 PF⊥y 轴于 F,PH⊥x 轴于 H,则有 d1=
4
1 a2,又 AF=OF
﹣OA=PH﹣OA=d1﹣1=
4
1 a2﹣1,PF=a,在 Rt△PAF 中,利用勾股定理得到 PA=d2=
4
1 a2+1,
即有结论 d2=d1+1;
(3)△PAC 的周长=PC+PA+5,由(2)得到△PAC 的周长=PC+PH+6,要使 PC+PH 最小,
则 C、P、H 三点共线,P 点坐标为(3,
4
9 ),此时 PC+PH=5,得到△PAC 的周长的最小值
=5+6=11.
解答:解:(1)设抛物线的解析式:y=ax2,
∵拋物线经过点 B(﹣4,4),
∴4=a•42,解得 a=
4
1 ,
所以抛物线的解析式为:y=
4
1 x2;
过 点 B 作 BE⊥y 轴 于 E , 过 点 C 作 CD⊥y 轴 于 D , 如 图 ,
∵点 B 绕点 A 顺时针方向 90°得到点 C,
∴Rt△BAE≌Rt△ACD,
∴AD=BE=4,CD=AE=OE﹣OA=4﹣1=3,
∴OD=AD+OA=5,
∴C 点坐标为(3,5);
(2)设 P 点坐标为(a,b),过 P 作 PF⊥y 轴于 F,PH⊥x 轴于 H,如图,
∵点 P 在抛物线 y=
4
1 x2 上,
∴b=
4
1 a2,
∴d1=
4
1 a2,
∵AF=OF﹣OA=PH﹣OA=d1﹣1=
4
1 a2﹣1,PF=a,
在 Rt△PAF 中,PA=d2= 22222 )24
1( aaPFAF =
4
1 a2+1,
∴d2=d1+1;
(3)由(1)得 AC=5,
∴△PAC 的周长=PC+PA+5
=PC+PH+6,
要使 PC+PH 最小,则 C、P、H 三点共线,
∴此时 P 点的横坐标为 3,把 x=3 代入 y=
4
1 x2,得到 y=
4
9 ,
即 P 点坐标为(3,
4
9 ),此时 PC+PH=5,
∴△PAC 的周长的最小值=5+6=11.
点评:本题考查了点在抛物线上,点的横纵坐标满足二次函数的解析式和顶点在原点的二次
函数的解析式为:y=ax2;也考查了旋转的性质、勾股定理以及两点之间线段最短..
47. (2011•乐山)已知顶点为 A(1,5)的抛物线 y=ax2+bx+c 经过点 B(5,1).
(1)求抛物线的解析式;
(2)如图(1),设 C,D 分别是 x 轴、y 轴上的两个动点,求四边形 ABCD 的周长;
(3)在(2)中,当四边形 ABCD 的周长最小时,作直线 CD.设点 P(x,y)(x>0)是
直线 y=x 上的一个动点,Q 是 OP 的中点,以 PQ 为斜边按图(2)所示构造等腰直角三角
形 PRQ.
①当△PBR 与直线 CD 有公共点时,求 x 的取值范围;
②在①的条件下,记△PQR 与△COD 的公共部分的面积为 S.求 S 关于 x 的函数关系式,
并求 S 的最大值.
考点:二次函数综合题。
专题:综合题。
分析:(1)可设顶点式,将顶点为 A(1,5),点 B(5,1)代入求出抛物线的解析式;
(2)线段 AB 的长是确定的,由于点 C,D 是两个动点,所以 BC,CD,DA 的长是不
确定的,只能用 4 2 +BC+CD+DA 表示四边形的周长;
(3)作 B 关于 x 轴对称点 B′,A 关于 y 轴对称点 A′,连接 A′B′,与 x 轴,y 轴交于 C、
D 点,此时四边形 ABCD 周长最小,求出 CD 的解析式,求出 CD 与直线 y=x 的交点坐标,
得到△PQR 与直线 y=x 有公共点时 x 的取值范围,以及公共部分的面积 S 与 x 之间的函数
关系式.
解答:解:(1)∵抛物线的顶点为 A(1,5),
∴设抛物线的解析式为 y=a(x﹣1)2+5,
将点 B(5,1)代入,得 a(5﹣1)2+5=1,
解得 a=﹣ 1
4
,
∴y=﹣ 1
4 x2+ 1
2 x+19
4
;
(2)四边形 ABCD 的周长为 AB+BC+CD+DA,
其中 AB=4 2 ,因为 C,D 是 x 轴与 y 轴上的动点,所以 BC,CD,DA 的长不是确定
的,
故四边形 ABCD 的周长表示为:4 2 +BC+CD+DA.
(3)①点 B 关于 x 轴的对称点 B′(5,﹣1),点 A 关于 y 轴的对称点 A′(﹣1,5),连
接 A′B′,与 x 轴,y 轴交于 C,D 点,
∴CD 的解析式为:y=﹣x+4,
联立 4y x
y x
,
得: 2
2
x
y
,
∵点 P 在 y=x 上,点 Q 是 OP 的中点,
∴要使等腰直角三角形与直线 CD 有公共点,则 2≤x≤4.
故 x 的取值范围是:2≤x≤4.
②如图:
点 E(2,2),当 EP=EQ 时,x﹣2=2﹣ 1
2 x,得:x= 8
3
,
当 2≤x≤ 8
3
时,S= 1
2 PR•RQ﹣ 1
2 EP2= 1
2
(x﹣ 1
2 x)•(x﹣ 1
2 x)﹣ 1
2 • 2 (x﹣2)• 2
(x﹣2),
S=﹣ 7
8 x2+4x﹣4,
当 x=16
7
时,S 最大= 4
7
.
当 8
3 ≤x≤4 时,S= 1
2 EQ2= 1
2 • 2 (2﹣ 1
2 x)• 2 (2﹣ 1
2 x),
S= 1
4
(x﹣4)2,
当 x= 8
3
时,S 最大= 4
9
.
故 S 的最大值为: 4
7
.
点评:本题考查的是二次函数的综合题,(1)利用顶点式求出二次函数的解析式,(2)确定
四边形的周长,(3)根据对称性求出 CD 的解析式,然后求出 x 的取值范围和 S 与 x 的函数
关系.
48. (2011 福建福州,22,14 分)已知,如图,二次函数 y=ax2+2ax﹣3a(a≠0)图象的顶
点为 H,与 x 轴交于 A.B 两点(B 在 A 点右侧),点 H.B 关于直线 l: 3 33y= x+ 对称.
(1)求 A.B 两点坐标,并证明点 A 在直线 l 上;
(2)求二次函数解析式;
(3)过点 B 作直线 BK∥AH 交直线 l 于 K 点,M.N 分别为直线 AH 和直线 l 上的两个动点,
连接 HN、NM、MK,求 HN+NM+MK 和的最小值.
考点:二次函数综合题;解二元一次方程组;待定系数法求二次函数解析式;抛物线与 x
轴的交点;图象法求一元二次方程的近似根;勾股定理.
分析:(1)求出方程 ax2+2ax﹣3a=0(a≠0),即可得到 A 点坐标和 B 点坐标;把 A 的坐标代
入直线 l 即可判断 A 是否在直线上;
(2)根据点 H.B 关于过 A 点的直线 l: 3 33y= x+ 对称,得出 AH=AB=4,过顶点 H 作
HC⊥AB 交 AB 于 C 点,求出 AC 和 HC 的长,得出顶点 H 的坐标,代入二次函数解析式,
求出 a,即可得到二次函数解析式;
(3)解方程组
3 33
3 3
y= x+
y= x-
,即可求出 K 的坐标,根据点 H.B 关于直线 AK 对称,得
出 HN+MN 的最小值是 MB,过点 K 作直线 AH 的对称点 Q,连接 QK,交直线 AH 于 E,得
到 BM+MK 的最小值是 BQ,即 BQ 的长是 HN+NM+MK 的最小值,由勾股定理得 QB=8,
即可得出答案.
解答:解:(1)依题意,得 ax2+2ax﹣3a=0(a≠0),
解得 x1=﹣3,x2=1,
∵B 点在 A 点右侧,
∴A 点坐标为(﹣3,0),B 点坐标为(1,0),
答:A.B 两点坐标分别是(﹣3,0),(1,0).
证明:∵直线 l: 3 33y= x+ ,当 x=﹣3 时, 3 3 03y= -3 + =( ) ,
∴点 A 在直线 l 上.
(2)解:∵点 H.B 关于过 A 点的直线 l: 3 33y= x+ 对称,
∴AH=AB=4,
过顶点 H 作 HC⊥AB 交 AB 于 C 点,
则 AC= 1
2 AB=2,HC= 2 3 ,
∴顶点 H 1 2 3- , ,代入二次函数解析式,解得 3
2a=- .
∴二次函数解析式为 23 3 332 2y=- x - x+ ,
答:二次函数解析式为 23 3 332 2y=- x - x+ .
(3)解:直线 AH 的解析式为 3 3 3y= x+ ,
直线 BK 的解析式为 3 3y= x- ,
由 3 3 3
3 3
y= x+
y= x-
,解得
3
2 3
x=
y=
,即 3 2 3K , ,则 BK=4.
∵点 H.B 关于直线 AK 对称,
∴HN+MN 的最小值是 MB,KD=KE= 2 3 ,
过点 K 作直线 AH 的对称点 Q,连接 QK,交直线 AH 于 E,
则 QM=MK,QE=EK= 2 3 ,AE⊥QK,
∴BM+MK 的最小值是 BQ,即 BQ 的长是 HN+NM+MK 的最小值,
∵BK∥AH,
∴∠BKQ=∠HEQ=90°,
由勾股定理得 QB=8,
∴HN+NM+MK 的最小值为 8,
答 HN+NM+MK 和的最小值是 8.
点评:本题主要考查对勾股定理,解二元一次方程组,二次函数与一元二次方程,二次函数
与 X 轴的交点,用待定系数法求二次函数的解析式等知识点的理解和掌握,综合运用这些
性质进行计算是解此题的关键,此题是一个综合性比较强的题目,有一定的难度.
49. 2011 福建龙岩,24,13 分)如图,已知抛物线 24
9y x bx c 与 x 轴相交于 A、B 两
点,其对称轴为直线 x=2,且与 x 轴交于点 D,AO=1.
(1)填空:b= .c= ,点 B 的坐标为( , ):
(2)若线段 BC 的垂直平分线 EF 交 BC 于点 E,交 x 轴于点 F.求 FC 的长;
(3)探究:在抛物线的对称轴上是否存在点 P,使⊙P 与 x 轴、直线 BC 都相切?若存在,
请求出点 P 的坐标;若不存在,请说明理由.
考点:二次函数综合题;解二元一次方程组;二次函数图象上点的坐标特征;待定系数
法求二次函数解析式;线段垂直平分线的性质;勾股定理.
分析:(1)根据对称轴和 OA=1 求出 A、B 的坐标,代入解析式求出 b、c 即可;
(2)求出 C(2,4)求得 E 的坐标为(3.5,2)和直线 BC 的表达式为 4 30
3 3y x ,设
直线 EF 的表达式为 y=kx+b,根据 EF 为 BC 的中垂线求出 3
4k 和 5
8b 推出直线 EF 的表
达式为 3 5
4 8y x ,令 y=0,得 5
6x 即可求出答案;
(3)作∠OBC 的平分线交 DC 于点 P,设 P(2,a),则 P 到 x 轴的距离等于 P 到直线 BC
的距离(用到点到直线的距离公式)求出 a 即可.
解答:(1)解:∵抛物线 24
9y x bx c 与 x 轴相交于 A、B 两点,其对称轴为直线
x=2,且与 x 轴交于点 D,AO=1,
∴A(﹣1,0),B(5,0),
代入解析式得:
28
9
40 9
b
b c
,解得:b=16
9
,c= 20
9
,
故答案为 16
9
, 20
9
,5,0.
(2)解:由(1)求得 2 24 16 20 4 ( 2) 49 9 9 9y x x x ,
∴C(2,4)
∵E 为 BC 的中点,由中点坐标公式求得 E 的坐标为(3.5,2),
直线 BC 的表达式为 4 30
3 3y x ,
整理得 4x+3y﹣20=0
设直线 EF 的表达式为 y=kx+b,
∵EF 为 BC 的中垂线,∴EF⊥BC,∴ 3
4k ,
把 E(3.5,2)代入求得 5
8b ,∴直线 EF 的表达式为 3 5
4 8y x ,
在 3 5
4 8y x 中,令 y=0,得 5
6x ,∴F( 5
6
,0),
∴FC=FB= 5 255 6 6
,答:FC 的长是 25
6
.
(3)解:存在,
作∠OBC 的平分线交 DC 于点 P,则 P 满足条件,
设 P(2,a),则 P 到 x 轴的距离等于 P 到直线 BC 的距离(用到点到直线的距离公式),
∴
2 2
4 2 3 20 3 12
54 3
a aa
,∴5|a|=|3a﹣12|,
∴5a=3a﹣12 或 5a=﹣3a+12,解得 a=﹣6 或 a= 3
2
,∴P(2,﹣6)或 P(2, 3
2
),
答:在抛物线的对称轴上存在点 P,使⊙P 与 x 轴、直线 BC 都相切,点 P 的坐标是(2,﹣
6),(2, 3
2
).
点评:本题主要考查对解二元一次方程组,二次函数图象上点的坐标特征,用待定系数
法求二次函数的解析式,勾股定理,线段的垂直平分线定理等知识点的理解和掌握,熟练地
运用这些性质进行计算是解此题的关键.
50.(2010 福建泉州,26,14 分)如图 1,在第一象限内,直线 y=mx 与过点 B(0,1)且
平行于 x 轴的直线 l 相交于点 A,半径为 r 的⊙Q 与直线 y=mx、x 轴分别相切于点 T、E,
且与直线 l 分别交于不同的 M、N 两点.
(1)当点 A 的坐标为( 3
3
,p)时,
①填空:p= 1 ,m= 3 ,∠AOE= 60° .
②如图 2,连接 QT、QE,QE 交 MN 于点 F,当 r=2 时,试说明:以 T、M、E、N 为顶点
的四边形是等腰梯形;
(2)在图 1 中,连接 EQ 并延长交⊙Q 于点 D,试探索:对 m、r 的不同取值,经过 M、D、
N 三点的抛物线 y=ax2+bx+c,a 的值会变化吗?若不变,求出 a 的值;若变化.请说明理由.
考点二次函数综合题;一次函数综合题;等边三角形的判定与性质;平行四边形的判定与性
质;等腰梯形的判定;切线的性质;解直角三角形。
分析(1)由点 A( 3
3
,p)在直线 l 上,得到 p=1;点 A 在直线 y=mx 上,得到 m= 3 ;
在 Rt△OBA 中,OB=1,AB= 3
3
,OA= 2 3
3
,得到∠AOE=60°;
(2)连接 TM,ME,EN,ON,根据切线的性质得到 QE⊥x 轴,QT⊥OT,由 QE⊥MN,
得到 MF=NF,而 r=2,EF=1,则四边形 QNEM 为平行四边形,即 QN∥ME;同时有△QEN
为等边三角形,则∠NQE=60°,∠QNF=30°;在四边形 OEQT 中,∠QTO=∠QEO=90°,
∠TOE=60°,可求出∠TQE=120°,于是有∠TQE+∠NQE=120°+60°=180°,即 T、Q、N 三
点共线,得到 TN 为直径;得到∠TMN=90°,得到 TN∥ME,所以∠MTN=60°=∠TNE,得
到以 T、M、E、N 为顶点的四边形是等腰梯形;
(3)连 DM,ME,根据垂径定理和圆周定理的推论得到∠DME=90°,DM 垂直平分 MN,
所以 Rt△MFD∽Rt△EFM,得到 MF2=EF•FD,设 D(h,k),(h>0,k=2r),则过 M、D、
N 三点的抛物线的解析式为:y=a(x﹣h)2+k,令 y=1,得到 x1=h﹣ 1 k
a
,x2=h+ 1 k
a
,
则 MF= 1
2
MN= 1 k
a
,得到( 1 k
a
)2=1•(k﹣1),解得 a=﹣1.
解答解:(1)∵点 A 的坐标为( 3
3
,p),点 A 在直线 l 上,
∴p=1,即点 A 坐标为( 3
3
,1);
而点 A 在直线 y=mx 上,
∴1= 3
3 m,解得 m= 3 ;
在 Rt△OBA 中,OB=1,AB= 3
3
,
∴OA= 2 3
3
,
∴∠AOB=30°,
∴∠AOE=60°.
故答案为 1, 3 ,60°;
(2)连接 TM,ME,EN,ON,
如图,
∵OE 和 OP 是⊙Q 的切线,
∴QE⊥x 轴,QT⊥OT,即∠QTA=90°,
而 l∥x 轴,
∴QE⊥MN,
∴MF=NF,
又∵当 r=2,EF=1,
∴QF=2﹣1=1,
∴四边形 QNEM 为平行四边形,即 QN∥ME,
∴NQ=NE,即△QEN 为等边三角形,
∴∠NQE=60°,∠QNF=30°,
在四边形 OEQT 中,∠QTO=∠QEO=90°,∠TOE=60°,
∴∠TQE=360°﹣90°﹣90°﹣60°=120°,
∴∠TQE+∠NQE=120°+60°=180°,
∴T、Q、N 三点共线,即 TN 为直径,
∴∠TMN=90°,
∴TN∥ME,
∴∠MTN=60°=∠TNE,
∴以 T、M、E、N 为顶点的四边形是等腰梯形;
(3)对 m、r 的不同取值,经过 M、D、N 三点的抛物线 y=ax2+bx+c,a 的值不会变化.理
由如下:
连 DM,ME,如图,
∵DM 为直径,
∴∠DME=90°,
而 DM 垂直平分 MN,
∴Rt△MFD∽Rt△EFM,
∴MF2=EF•FD,
设 D(h,k),(h>0,k=2r),则过 M、D、N 三点的抛物线的解析式为:y=a(x﹣h)2+k,
又∵M、N 的纵坐标都为 1,
当 y=1,a(x﹣h)2+k=1,解得 x1=h﹣ 1 k
a
,x2=h+ 1 k
a
,
∴MN=2 1 k
a
,
∴MF= 1
2
MN= 1 k
a
,
∴( 1 k
a
)2=1•(k﹣1),
∵k>1,
∴1 k
a
=k﹣1,
∴a=﹣1.
点评本题考查了抛物线的顶点式:y=a(x﹣h)2+k,其中顶点坐标为(h,k);也考查了等
腰梯形的判定和三角形相似的判定与性质以及垂径定理.
51. (2011 福建省三明市,22,12 分)如图,抛物线 y=ax2﹣4ax+c(a≠0)经过 A(0,﹣1),
B(5,0)两点,点 P 是抛物线上的一个动点,且位于直线 AB 的下方(不与 A,B 重合),
过点 P 作直线 PQ⊥x 轴,交 AB 于点 Q,设点 P 的横坐标为 m.
(1)求 a,c 的值;
(2)设 PQ 的长为 S,求 S 与 m 的函数关系式,写出 m 的取值范围;
(3)以 PQ 为直径的圆与抛物线的对称轴 l 有哪些位置关系?并写出对应的 m 取值范围.(不
必写过程)
考点:二次函数综合题。
分析:(1)利用待定系数法把点 A、B 的坐标代入抛物线表达式解二元一次方程组即可;
(2)先求出直线 AB 的解析式,然后分别求出点 P 与点 Q 的坐标,则 PQ 的长度 S 就等于
点 Q 的纵坐标减去点 P 的纵坐标,然后整理即可;
(3)根据直线与圆的位置关系有相离、相切与相交共三种情况,又点 P 可以在对称轴左边
也可以在对称轴右边,进行讨论列式求解即可.
解答:解:∵抛物线 y=ax2﹣4ax+c 过 A(0,﹣1),B(5,0)
∴ 1
25 20 0
c
a a c
,
解得:
1
5
1
a
c
,
故 ac 的值分别为 1
5
,﹣1,
抛物线的解析式是 y= 1
5 x2﹣ 4
5 x﹣1;
(2)∵直线 AB 经过 A(0,﹣1),B(5,0),
∴直线 AB 的解析式为 y= 1
5 x﹣1,
由(1)知抛物线的解析式为:y= 1
5 x2﹣ 4
5 x﹣1,
∵点 P 的横坐标为 m,点 P 在抛物线上,点 Q 在直线 AB 上,PQ⊥x 轴,
∴P(m, 1
5 m2﹣ 4
5 m﹣1),Q(m, 1
5 m﹣1),
∴S=PQ=( 1
5 m﹣1)﹣( 1
5 m2﹣ 4
5 m﹣1),
即 S=﹣ 1
5 m2+m(0<m<5);
(3)抛物线的对称轴 l 为:x=2,
以 PQ 为直径的圆与抛物线的对称轴 l 的位置关系有:
相离、相切、相交三种关系
相离时:|m﹣2|> 1
2
(﹣ 1
5 m2+m),
解得 0<m<15 145
2
或 5 105
2
<m<5;
相切时:|m﹣2|= 1
2
(﹣ 1
5 m2+m),
解得 m=15 145
2
或 m= 5 105
2
;
相交时:|m﹣2|< 1
2
(﹣ 1
5 m2+m),
解得15 145
2
<m< 5 105
2
.
点评:本题考查了待定系数法,直线与二次函数相交的问题,直线与圆的位置关系,综合性
较强,对同学们的能力要求较高,(3)中要注意分点 P 有在对称轴左边与右边的两种情况,
容易漏解而导致出错.
52.(2011 甘肃兰州,28,12 分)如图所示,在平面直角坐标系 xoy 中,正方形 OABC 的边
长为 2cm,点 A、C 分别在 y 轴的负半轴和 x 轴的正半轴上,抛物线 2y ax bx c 经过点
A、B 和 D(4, 2
3
).
(1)求抛物线的表达式.
(2)如果点 P 由点 A 出发沿 AB 边以 2cm/s 的速度向点 B 运动,同时点 Q 由点 B 出发,沿
BC 边以 1cm/s 的速度向点 C 运动,当其中一点到达终点时,另一点也随之停止运动。设 S=PQ2
(cm2).
①试求出 S 与运动时间 t 之间的函数关系式,并写出 t 的取值范围;
②当 S 取 5
4
时,在抛物线上是否存在点 R,使得以点 P、B、Q、R 为顶点的四边形是平行
四边形?如果存在,求出 R 点的坐标;如果不存在,请说明理由.
(3)在抛物线的对称轴上求点 M,使得 M 到 D、A 的距离之差最大,求出点 M 的坐标.
x
y
A
O
B
P Q
C
D
考点:二次函数综合题;待定系数法求一次函数解析式;二次函数图象上点的坐标特征;
待定系数法求二次函数解析式;勾股定理;平行四边形的性质.
分析:(1)设抛物线的解析式是 y=ax2+bx+c,求出 A、B、D 的坐标代入即可;(2)①
由勾股定理即可求出,②假设存在点 R,可构成以 P、B、R、Q 为顶点的平行四边形,求出
P、Q 的坐标,再分为三种情况:A、B、C 即可根据平行四边形的性质求出 R 的坐标.(3)
A 关于抛物线的对称轴的对称点为 B,过 B、D 的直线与抛物线的对称轴的交点为所求 M,
求出直线 BD 的解析式,把抛物线的对称轴 x=1 代入即可求出 M 的坐标.
解答:(1)解:设抛物线的解析式是 y=ax2+bx+c,
当 x=0 时,y=﹣2,
∴点 A 的坐标是(0,﹣2),
∵正方形的边长 2,
∴B 的坐标(2,﹣2),把 A(0,﹣2),B(2,﹣2),D(4,﹣ 2
3
)代入得:
2
4 2 2
c
a b c
且
4 2 2
216 4 3
a b c
a b c
,
解得 a= 1
6
,b=﹣ 1
3
,c=﹣2
∴抛物线的解析式为: 21 1 26 3y x x ,
答:抛物线的解析式为: 21 1 26 3y x x .
(2)解:①由图象知:PB=2﹣2t,BQ=t,
∴S=PQ2=PB2+BQ2,
=(2﹣2t)2+t2,
即 S=5t2﹣8t+4(0≤t≤1).
答:S 与运动时间 t 之间的函数关系式是 S=5t2﹣8t+4,t 的取值范围是 0≤t≤1.
②解:假设存在点 R,可构成以 P、B、R、Q 为顶点的平行四边形.
∵S=5t2﹣8t+4(0≤t≤1),
∴当 S= 5
4
时,5t2﹣8t+4= 5
4
,得 20t2﹣32t+11=0,
解得 t= 1
2
,t= 11
10
(不合题意,舍去),
此时点 P 的坐标为(1,﹣2),Q 点的坐标为(2,﹣ 3
2
)
若 R 点存在,分情况讨论:
【A】假设 R 在 BQ 的右边,这时 QR=PB,RQ∥PB,则 R 的横坐标为 3,R 的纵坐标为﹣ 3
2
,
即 R(3,﹣ 3
2
),代入 21 1 26 3y x x ,左右两边相等,
∴这时存在 R(3,﹣ 3
2
)满足题意;
【B】假设 R 在 BQ 的左边,这时 PR=QB,PR∥QB,
则:R 的横坐标为 1,纵坐标为﹣ 3
2
,即(1,﹣ 3
2
),
代入 21 1 26 3y x x ,左右两边不相等,R 不在抛物线上;
【C】假设 R 在 PB 的下方,这时 PR=QB,PR∥QB,则:R(1,﹣ 5
2
)代入, 21 1 26 3y x x
左右不相等,∴R 不在抛物线上.
综上所述,存点一点 R(3,﹣ 3
2
)满足题意.
答:存在,R 点的坐标是(3,﹣ 3
2
).
(3)解:如图,M′B=M′A,
∵A 关于抛物线的对称轴的对称点为 B,过 B、D 的直线与抛物线的对称轴的交点为所求 M,
设直线 BD 的解析式是 y=kx+b,把 B、D 的坐标代入得:
2 2
24 3
k b
k b
,
解得:k= 2
3
,b=﹣10
3
,∴y= 2
3 x﹣10
3
,抛物线 21 1 26 3y x x 的对称轴是 x=1,
把 x=1 代入得: 8
3y ∴M 的坐标为(1, 8
3
);
答:M 的坐标为(1, 8
3
).
点评:本题主要考查了用待定系数法求一次函数和二次函数的解析式,勾股定理,平行
四边形的性质,二次函数图象上点的坐标特征等知识点,解此题的关键是综合运用这些知识
进行计算.此题综合性强,是一道难度较大的题目.
53. (2011 广东省茂名,25,8 分)如图,在平面直角坐标系 xoy 中,已知抛物线经过点 A
(0,4),B(1,0),C(5,0),抛物线对称轴 l 与 x 轴相交于点 M.
(1)求抛物线的解析式和对称轴;
(2)设点 P 为抛物线(x>5)上的一点,若以 A、O、M、P 为顶点的四边形四条边的长度
为四个连续的正整数,请你直接写出点 P 的坐标;
(3)连接 AC.探索:在直线 AC 下方的抛物线上是否存在一点 N,使△NAC 的面积最大?
若存在,请你求出点 N 的坐标;若不存在,请你说明理由.
考点:二次函数综合题。
分析:(1)抛物线经过点 A(0,4),B(1,0),C(5,0),可利用两点式法设抛物线的解
析式为 y=a(x﹣1)(x﹣5),代入 A(0,4)即可求得函数的解析式,则可求得抛物线的对
称轴;
(2)由已知,可求得 P(6,4),由题意可知以 A、O、M、P 为顶点的四边形有两条边 AO=4、
OM=3,又知点 P 的坐标中 x>5,所以 MP>2,AP>2;因此以 1、2、3、4 为边或以 2、3、
4、5 为边都不符合题意,所以四条边的长只能是 3、4、5、6 的一种情况,则分析求解即可
求得答案;
(3)在直线 AC 的下方的抛物线上存在点 N,使△NAC 面积最大.设 N 点的横坐标为 t,
此时点 N(t, 4
5
t2﹣ 24
5
t+4)(0<t<5),再求得直线 AC 的解析式,即可求得 NG 的长与
△ACN 的面积,由二次函数最大值的问题即可求得答案.
解答:解:(1)根据已知条件可设抛物线的解析式为 y=a(x﹣1)(x﹣5),
把点 A(0,4)代入上式得:a= 4
5
,
∴y= 4
5
(x﹣1)(x﹣5)= 4
5
x2﹣ 24
5
x+4= 4
5
(x﹣3)2﹣16
5
,
∴抛物线的对称轴是:x=3;
(2)由已知,可求得 P(6,4),
由题意可知以 A、O、M、P 为顶点的四边形有两条边 AO=4、OM=3,
又∵点 P 的坐标中 x>5,
∴MP>2,AP>2;
∴以 1、2、3、4 为边或以 2、3、4、5 为边都不符合题意,
∴四条边的长只能是 3、4、5、6 的一种情况,
在 Rt△AOM 中, 2 2 2 24 3 5AM OA OM
∵抛物线对称轴过点 M,
∴在抛物线 x>5 的图象上有关于点 A 的对称点与 M 的距离为 5,
即 PM=5,此时点 P 横坐标为 6,即 AP=6;
故以 A、O、M、P 为顶点的四边形的四条边长度分别是四个连续的正整数 3、4、5、6 成立,
即 P(6,4);
(3)在直线 AC 的下方的抛物线上存在点 N,使△NAC 面积最大.
设 N 点的横坐标为 t,此时点 N(t, 4
5
t2﹣ 24
5
t+4)(0<t<5),
过点 N 作 NG∥y 轴交 AC 于 G;由点 A(0,4)和点 C(5,0)可求出直线 AC 的解析式为:
y=﹣ 4
5
x+4;
把 x=t 代入得:y=﹣ 4
5
x+4,则 G(t,﹣ 4
5
t+4),
此时:NG=﹣ 4
5
x+4﹣( 4
5
t2﹣ 24
5
t+4)=﹣ 4
5
t2+ 20
5
t,
∴S△ACN= 1
2
NG•OC= 1
2
(﹣ 4
5
t2+ 20
5
t)×5=﹣2t2+10t=﹣2(t﹣ 5
2
)2+ 25
2
,
∴当 t= 5
2
时,△CAN 面积的最大值为 25
2
,
由 t= 5
2
,得:y= 4
5
t2﹣ 24
5
t+4=﹣3,
∴N( 5
2
,﹣3).
点评:此题考查了待定系数法求二次函数的解析式,勾股定理以及三角形面积的最大值问
题.此题综合性很强,难度很大,解题的关键是方程思想与数形结合思想的应用.
54. (2011 福建省漳州市,26,14 分)如图 1,抛物线 y=mx2﹣11mx+24m (m<0)与 x 轴
交于 B、C 两点(点 B 在点 C 的左侧),抛物线另有一点 A 在第一象限内,且∠BAC=90°.
(1)填空:OB= 3 ,OC= 8 ;
(2)连接 OA,将△OAC 沿 x 轴翻折后得△ODC,当四边形 OACD 是菱形时,求此时抛物
线的解析式;
(3)如图 2,设垂直于 x 轴的直线 l:x=n 与(2)中所求的抛物线交于点 M,与 CD 交于点
N,若直线 l 沿 x 轴方向左右平移,且交点 M 始终位于抛物线上 A、C 两点之间时,试探究:
当 n 为何值时,四边形 AMCN 的面积取得最大值,并求出这个最大值.
考点:二次函数综合题。
分析:(1)根据二次函数与 x 轴交点坐标求法,解一元二次方程即可得出;
(2)利用菱形性质得出 AD⊥OC,进而得出△ACE∽△BAE,即可得出 A 点坐标,进而求
出二次函数解析式;
(3)首先求出过 C、D 两点的坐标的直线 CD 的解析式,进而利用 S 四边形 AMCN=S△AMN+S△CMN
求出即可.
解答:解:(1)∵抛物线 y=mx2﹣11mx+24m (m<0)与 x 轴交于 B、C 两点(点 B 在点 C
的左侧),
∴抛物线与 x 轴的交点坐标为:0=mx2﹣11mx+24m,
解得:x1=3,x2=8,
∴OB=3,OC=8 (4 分);
(2)连接 OD,交 OC 于点 E,
∵四边形 OACD 是菱形,
∴AD⊥OC,OE=EC= 1
2 ×8=4,
∴BE=4﹣3=1,
又∵∠BAC=90°,
∴△ACE∽△BAE,
∴ AE CE
BE AE
,
∴AE2=BE•CE=1×4,
∴AE=2,…(6 分)
∴点 A 的坐标为 (4,2)…(7 分)
把点 A 的坐标 (4,2)代入抛物线 y=mx2﹣11mx+24m,得 m=﹣ 1
2
∴抛物线的解析式为 y=﹣ 1
2 x2+11
2 x﹣12; …(9 分)
(3)∵直线 x=n 与抛物线交于点 M,
∴点 M 的坐标为 (n,﹣ 1
2 n2+11
2 n﹣12),
由(2)知,点 D 的坐标为(4,﹣2),
则 C、D 两点的坐标求直线 CD 的解析式为 y= 1
2 x﹣4,
∴点 N 的坐标为 (n, 1
2 n﹣4),
∴MN=(﹣ 1
2 n2+11
2 n﹣12)﹣( 1
2 n﹣4)=﹣ 1
2 n2+5n﹣8,…(11 分)
∴S 四边形 AMCN=S△AMN+S△CMN= 1
2 MN•CE= 1
2
(﹣ 1
2 n2+5n﹣8)×4
=﹣(n﹣5)2+9 (13 分)
∴当 n=5 时,S 四边形 AMCN=9. (14 分)
点评:此题主要考查了二次函数与坐标轴交点坐标求法以及菱形性质和四边形面积求法等知
识,根据已知得出△ACE∽△BAE 是解决问题的关键.
55. (2011 广州,24,14 分)已知关于 x 的二次函数 y=ax2+bx+c(a>0)的图象经过点 C(0,1),
且与 x 轴交于不同的两点 A、B,点 A 的坐标是(1,0)
(1)求 c 的值;
(2)求 a 的取值范围;
(3)该二次函数的图象与直线 y=1 交于 C、D 两点,设 A、B、C、D 四点构成的四边
形的对角线相交于点 P,记△PCD 的面积为 S1,△PAB 的面积为 S2,当 00)的图象经过点 C(0,1),
且与 x 轴交于不同的两点 A、B,点 A 的坐标是(1,0)
(1)求 c 的值;
(2)求 a 的取值范围;
(3)该二次函数的图象与直线 y=1 交于 C、D 两点,设 A、B、C、D 四点构成的四边
形的对角线相交于点 P,记△PCD 的面积为 S1,△PAB 的面积为 S2,当 00)的图象经过点 C(0,1),
且与 x 轴交于不同的两点 A、B,点 A 的坐标是(1,0)
(1)求 c 的值;
(2)求 a 的取值范围;
(3)该二次函数的图象与直线 y=1 交于 C、D 两点,设 A、B、C、D 四点构成的四边
形的对角线相交于点 P,记△PCD 的面积为 S1,△PAB 的面积为 S2,当 00).(1)ΔABC 中边 BC 上高 AD=
((2)当 x= 时,PQ 恰好落
在边 BC 上(如图 1);(3)当 PQ 在Δ
ABC 外部时(如图 2),求 y 关于 x 的
函数关系式(注明 x 的取值范围),并
求出 x 为何值时 y 最大,最大值是多
少?
解:(1) 4AD ;··················································································· 2 分
(2) 2.4x (或12
5
);·················································································· 6 分
(3)设 BC 分别交 MP NQ, 于 E F, ,则四边形 MEFN 为矩形.
设 ME NF h , AD 交 MN 于G (如图 2)
GD NF h , 4AG h .
MN BC ∥ ,
A B
H
O
Q P
y
x
M
C
A B
H
O
Q
P
y
x
M
C
E
A
B C
M N
P Q
D
G
E F
AMN ABC△ ∽△ .
MN AG
BC AD
,即 4
6 4
x h
2 43h x .······················································· 8 分
y MN NF 2 43x x
22 4 (2.4 6)3 x x x .············································································10 分
配方得: 22 ( 3) 63y x .·········································································11 分
当 3x 时, y 有最大值,最大值是 6.
22. (宜昌)如图 1,已知四边形 OABC 中的三个顶点坐标为 O(0,0),A(0,n),C(m,0).动
点 P 从点 O 出发依次沿线段 OA,AB,BC 向点 C 移动,设移动路程为 z,△OPC 的面
积 S 随着 z 的变化而
变化的图象如图 2
所示.m,n 是常数,
m>1,n>0.(1)请
你确定 n 的值和点 B
的坐标;(2)当动点
P 是经过点 O,C 的
抛物线 y=ax 2 +bx
+c 的顶点,且在双曲线 y= 11
5x
上时,求这时四边形 OABC 的面积.
.解:(1) 从图中可知,当 P 从 O 向 A 运动时,△POC 的面积 S= 1
2
mz, z 由 0 逐步增
大到 2,则 S 由 0 逐步增大到 m,故 OA=2,n=2 . (1 分)
同理,AB=1,故点 B 的坐标是(1,2).(2 分)
(2)解法一:
∵抛物线 y=ax 2 +bx+c 经过点 O(0,0),C(m ,0),∴c=0,b=-am,(3 分)
∴抛物线为 y=ax 2 -amx,顶点坐标为(
2
m ,-1
4 am2).(4 分)
如图 1,设经过点 O,C,P 的抛物线为 l.
当 P 在 OA 上运动时,O,P 都在 y 轴上,
这时 P,O,C 三点不可能同在一条抛物线上,
∴这时抛物线 l 不存在, 故不存在 m 的值..①
(25 题图 1)
当点 P 与 C 重合时,双曲线 y= 11
5x
不可能经过 P,
故也不存在 m 的值.②(5 分)
(说明:①②任做对一处评 1 分,两处全对也只评一分)
当 P 在 AB 上运动时,即当 02,与 x 0 =
2
m ≤1 不合,舍去.(6 分)
③
容易求得直线 BC 的解析式是: 2 2
1 1
my xm m
,(7 分)
当 P 在 BC 上运动,设 P 的坐标为 (x 0 ,y 0 ),当 P 是顶点时 x 0 =
2
m ,
故得 y 0 = 0
2 2
1 1
mxm m
=
1
m
m
,顶点 P 为(
2
m ,
1
m
m ),
∵1< x 0 =
2
m 2,又∵P 在双曲线 y= 11
5x
上,
于是,
2
m ×
1
m
m
=11
5
,化简后得 5m 2 -22m+22=0,
解得 1
22 2 11
10m , 2
22 2 11
10m ,(8 分)
2 11 2, 22 2 11 20, 2
22 2 11 2,10m
与题意 2
查看更多