中考数学专题之数形结合
中考数学专题 数形结合
知识梳理
数形结合是把抽象的数学语言与直观的图形结合起来思索,使抽象思维和形象思维相结合,通过“以形助数”或“以数解形”可使复杂问题简单化,抽象的数学问题直观化、生动化,能够变抽象思维为形象思维,有助于把握数学问题的本质.另外,由于使用了数形结合的方法,很多问题便迎刃而解,且解法简捷,从而起到优化计算的目的.
华罗庚先生曾指出:“数与形本是相倚依,焉能分作两边飞;数缺形时少直觉,形少数时难入微;数形结合百般好,隔裂分家万事休.”这充分说明了数形结合数学学习中的重要性,是中考数学的一个最重要数学思想.
典型例题
一、在数与式中的应用
【例1】实数、b在数轴上的位置如图所示,化简=_________.
【分析】 由数轴上,b的位置可以得到<0,b>0且
3 B.k=3 C.k<3 D.无法确定
【分析】 如果根据b2-4c的符号来判别解的情况,本题将无从入手,可将原方程变形为x2+bx+c=k,从而理解成是两个函数的交点问题,即,由图象可知只要y=k<3就一定定与抛物线有两个不同的交点,所以答案选C.
【解】C
三、在函数中的应用
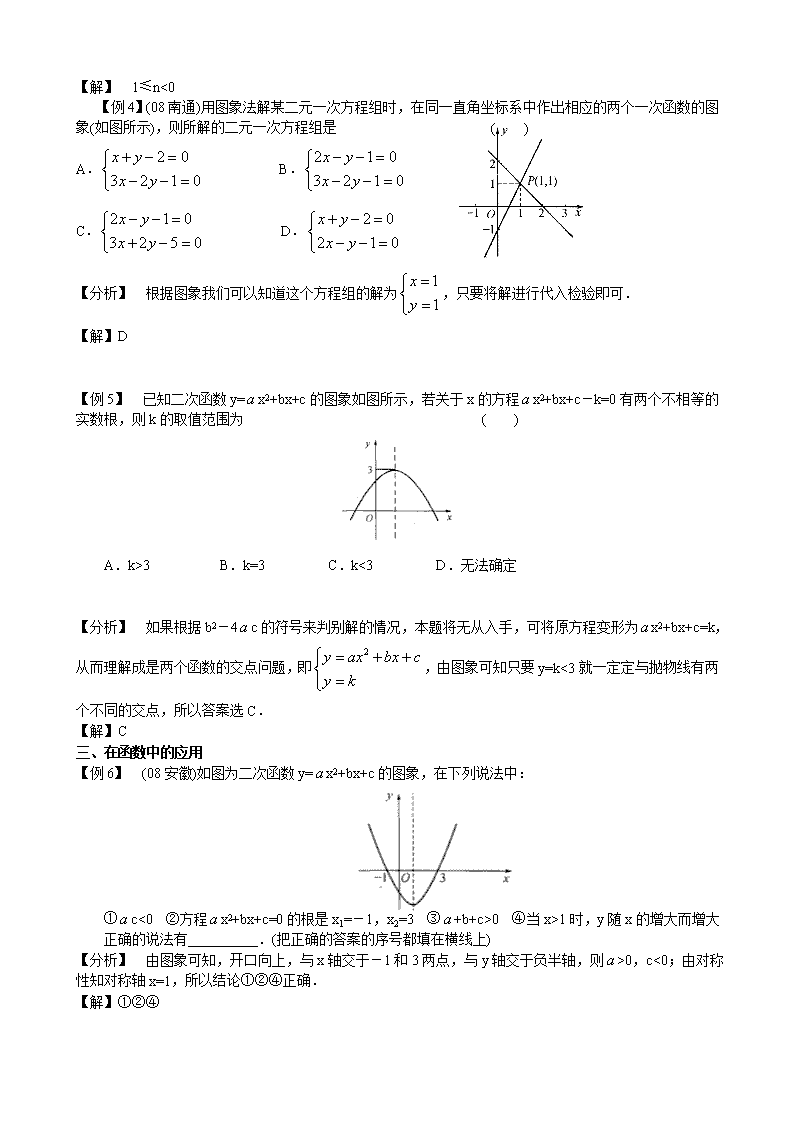
【例6】 (08安徽)如图为二次函数y=x2+bx+c的图象,在下列说法中:
①c<0 ②方程x2+bx+c=0的根是x1=-1,x2=3 ③+b+c>0 ④当x>1时,y随x的增大而增大
正确的说法有__________.(把正确的答案的序号都填在横线上)
【分析】 由图象可知,开口向上,与x轴交于-1和3两点,与y轴交于负半轴,则>0,c<0;由对称性知对称轴x=1,所以结论①②④正确.
【解】①②④
【例7】某跳水运动员进行10米跳台跳水训练时,身体(看成一点)在空中的运动路线如图所示,为经过原点O的一条抛物线(图中标出的数据为已知条件).要跳某个规定动作时,正常情况下,该运动员在空中的最高处距水面米,入水处距池边的距离为4米,同时,运动员在距水面高度为5米以前,必须完成规定的翻腾动作,并调整好入水姿势,否则就会出现失误,
(1)求这条抛物线的解析式;
(2)在某次试跳中,测得运动员在空中运动路线是如图抛物线,且运动员在空中调整好入水姿势时,距池边的水平距离为3导米,问此次跳水会不会失误?并通过计算说明理由.
【分析】(1)在给出的直角坐标系中,要确定抛物线的解析式,就要确定抛物线上三个点的坐标,如起跳点O(0,0),入水点(2,-10),最高点的纵点标为.
(2)求出抛物线的解析式后,要判断此次跳水会不会失误,
就是要看当该运动员在距池边水平距离为米,时,
该运动员距水面高度与5米的关系.
【解】(1)在给定的直角坐标系下,设最高点为A,入水点为B,抛物线的解析式为y=x2+bx+c,由图可知,O,B两点的坐标依次为(0,0)(2,-10),且顶点A的纵坐标为,则,解得或 抛物线的对称轴在y轴右侧,.又抛物线开口向下,,
,c=0,.
(2)当运动员在空中距池边距离为米时,即时,,此时运动员距水面高为.因此,试跳会出现失误.
四、在概率统计中的应用
【例8】(05江西)某报社为了解读者对本社一种报纸四个版面的喜欢情况,对读者作了一次问卷调查,要求读者选出自己最喜欢的一个版面,将所得数据整理后绘制成了如图所示的条形统计图:
(1)请写出从条形统计图中获得的一条信息;
(2)请根据条形统计图中的数据补全扇形统计图,并说明这两幅统计图各有什么特点;
(3)请你根据上述数据,对该报社提出一条合理的建议.
【分析】观察条形统计图可以计算出调查总人数,画扇形统计图需计算出第一版、第二版的百分比和圆心角,分别为,,建议可从不足的方面提出.
【解】(1)参加调查的人数为5000人;
(2)如图所示:条形统计图能清楚地表示出喜欢各版
面的读者人数.扇形统计图能清楚地表示出喜欢各版面的
读者人数占所调查的总人数的百分比.
(3)如:建议改进第二版的内容,提高文章质量,内容更贴近生活,形式更活泼些.
综合训练
1.“数轴上的点并不都表示有理数,如图中数轴上的点P所表示的数是”,这种说明问题的方式体现的数学思想方法叫做( )
A.代入法 B.数形结合 C.换元法 D.分类讨论
2.(08大连)如图,两温度计读数分别为我国某地今年2月份某天的最低气温与最高气温,那么这天的最高气温比最低气温高 ( )
A.5℃ B.7℃ C.12℃ D.-12℃
3.某人从A地向B地打长途电话6分钟,按通话时间收费,3分钟以内收费2.4元,此后每加1分钟加收1元,则表示电话费y(元)与通话时间(分)之间的关系的图象正确的是( )
4.若M,N,三点都在函数(k<0)的图象上,则y1,y2,y3的大小关系为( )
A.y2>y3>y1 B.y2>y1>y3 C.y3>y1>y2 D.y3>y2>y1
5.关于x的一元二次方程x2-x-n=0没有实数根,则抛物线y=x2-x-n的顶点在
A.第一象限 B.第二象限 C.第三象限 D.第四象限( )
6.(08临沂)若不等式组的解集为x<0,则的取值范围为 ( )
A.>0 B.=0 C.>4 D.=4
7.(08镇江)福娃们在一起探讨研究下面的题目:
函数y=x2-x+m(m为常数)的图象如图所示,如果x=时,y<0;那么x=-1时,函数值( )
下面是福娃们的讨论,请你解答该题.
贝贝:我注意到当x=0时,y=m>0.
晶晶:我发现图象的对称轴为x=
欢欢:我判断出x1<m D.y=m
8.如图,在平面直角坐标系中,∠AOB=150°,OA=OB=2,则点A、B的坐标分别是_________和_________.
9.在边长为的正方形中,挖掉一个边长为b的小正方形(>b)如图1,把余下的部分剪拼成一个矩形如图2,通过计算两个图形(阴影部分)的面积,验证了一个等式,则这个等式是_______________.
10.(08绍兴)如图,已知函数y=x+b和y=x+3的图象交点为P,则不等式x+b>x+3的解集为
__________.
11.方程组的解是__________.
12.(08广州)如图,为实数、b在数轴上的位置,化简.
13.(02南京)(1)阅读下面材料:点A、B在数轴上分别表示实数、b,A、B两点之间的距离表示为.当A、B两点中有一点在原点时,
不妨设点A在原点,如图1,;
当A、B两点都不在原点时,
①如图2,点A、B都在原点的右边;
②如图3,点A、B都在原点的左边,;
③如图4,点A、B在原点的两边,.
(2)回答下列问题:
①数轴上表示2和5的两点之间的距离是_______,数轴上表示-2和-5的两点之间的距离是_______,数轴上表示1和-3的两点之间的距离是________;
②数轴上表示x和-1的两点A和B之间的距离是_________,如果,那么x为__________;
③当代数式取最小值时,相应的x的取值范围是____________.
14.(08苏州)某厂生产一种产品,图①是该厂第一季度三个月产量的统计图,图②是这三个月的产量与第一季度总产量的比例分布统计图,统计员在制作图①、图②时漏填了部分数据.
根据上述信息,回答下列问题:
(1)该厂第一季度_________月份的产量最高.(2)该厂一月份产量占第一季度总产量的_______%.
(3)该厂质检科从第一季度的产品中随机抽样,抽检结果发现样品的合格率为98%.请你估计:该厂第一季度大约生产了多少件合格的产品?(写出解答过程)
15.(08恩施)如图所示,C为线段BD上一动点,分别过点B、D作AB⊥BD,ED⊥BD,连接AC、EC.已知AB=5,DE=1,BD=8;设CD=x.
(1)用含x的代数式表示AC+CE的长;
(2)请问点C满足什么条件时,AC+CE的值最小?
(3)根据(2)中的规律和结论,请构图求出代数式的最小值.
16.如图,已知抛物线与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,3)。
(1)求抛物线的解析式;
(2)设抛物线的顶点为D,在其对称轴的右侧的抛物线上是否存在点P,使得△PDC是等腰三角形?若存在,求出符合条件的点P的坐标;若不存在,请说明理由;
(3)若点M是抛物线上一点,以B、C、D、M为顶点的四边形是直角梯形,试求出点M的坐标.
综合训练参考答案
1.B 2.C 3.C 4.B 5.A 6.B 7.C
8. (2,0) 9.2-b2=(+b)(-b)
10.x>1 11.(0,-1)
12.原式=--b-(b-)=-2b
13.①3 3 4 ② 1或-3 ③-l≤x≤2
14.(1)三 (2)30 (3)(1900-38%)×98%=4900
15.(1)
(2)当A、C、E三点共线时,AC+CE的值最小
(3)如下图所示,作BD=12,过点B作AB⊥BD,过点D作ED⊥BD,使AB=2,ED=3,连结AE交BD于点C.AE的长即为代数式的最小值.
过点A作AF∥BD交ED的延长线于点F,得矩形ABDF,则AB=DF=2,AF=BD=12.所以即的最小值为13.
16.(1) 抛物线与y轴交于点C(0,3),设抛物线解析式为y=x2+bx+3(≠0)
根据题意,得,
解得,
· 抛物线的解析式为y=-x2+2x+3.
(2)存在. 由y=-x2+2x+3得,D点坐标为(1,4),对称轴为x=1.
①若以CD为底边,则PD=PC,设P点坐标为(x,y),根据勾股定理,
得x2+(3-y) 2=(x-1) 2+(4-y) 2,即y=4-x.又P点(x,y)在抛物线上,
4-x=-x2+2x+3,即x2-3x+1=0. 解得,因<1,应舍去.
,即点P坐标为.
②若以CD为一腰,因为点P在对称轴右侧的抛物线上,由抛物线对称性知,点P与点C关于直线x=1对称,此时点P坐标为(2,3).
符合条件的点P坐标为或(2,3).
(3)由B(3,0),C(0,3),D(1,4),根据勾股定理,得CB=,CD=,BD=.
CB2+CD2=BD2=20,∠BCD=90°,
设对称轴交x轴于点E,过C作CM⊥DE,交抛物线于点M,垂足为F,
在Rt△DCF中,
CF=DF=1,∠CDF=45°,
由抛物线对称性可知,∠CDM=2×45°=90°,点坐标M为(2,3),
DM∥BC,
四边形BCDM为直角梯形,
由∠BCD=90°及题意可知,以BC为一底时,顶点M在抛物线上的直角梯形只有上述一种情况;以CD为一底或以BD为一底,且顶点M在抛物线上的直角梯形均不存在.
综上所述,符合条件的点M的坐标为(2,3)坐标.