- 2021-05-10 发布 |
- 37.5 KB |
- 9页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
中考数学模拟试卷含答案
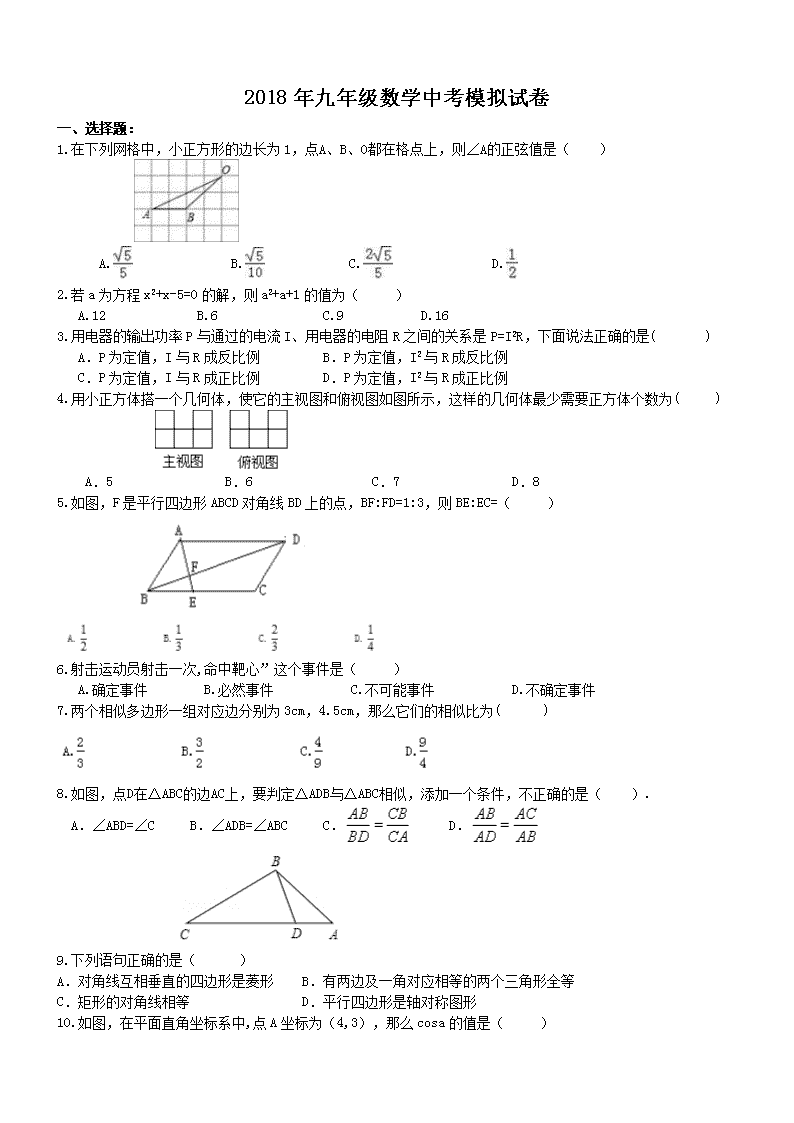
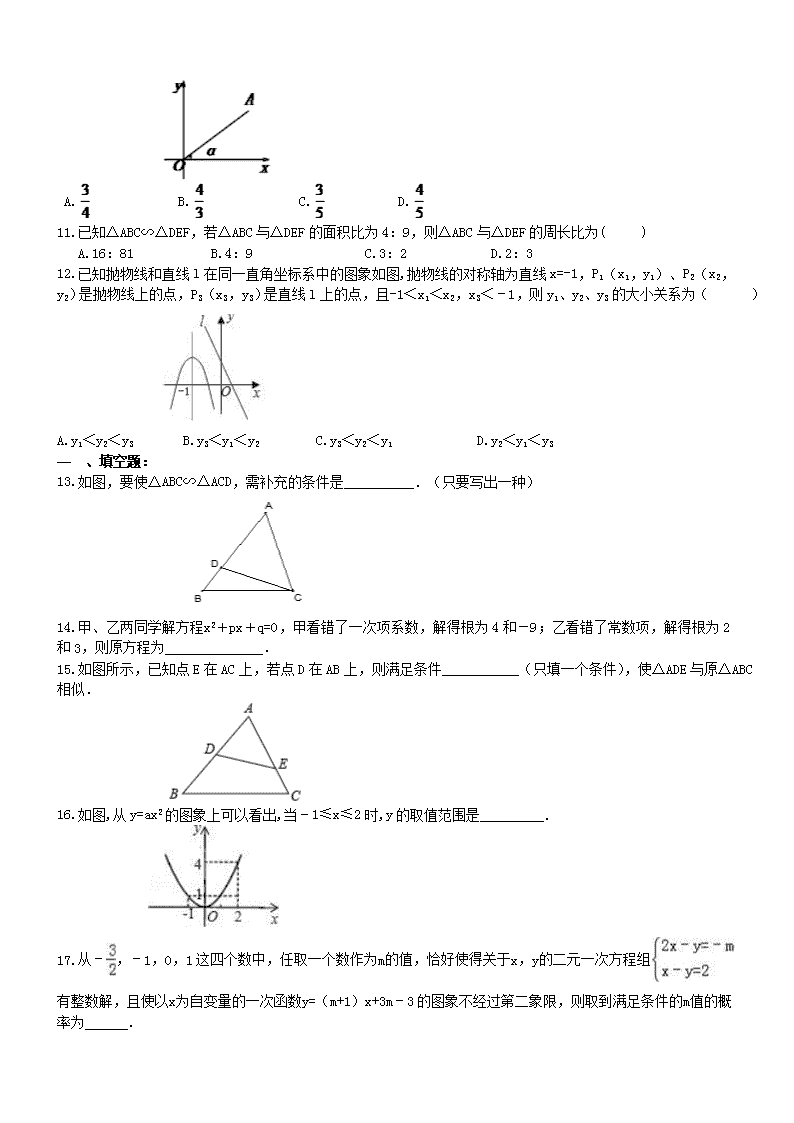
2018年九年级数学中考模拟试卷 一、选择题: 在下列网格中,小正方形的边长为1,点A、B、O都在格点上,则∠A的正弦值是( ) A. B. C. D. 若a为方程x2+x-5=0的解,则a2+a+1的值为( ) A.12 B.6 C.9 D.162 用电器的输出功率P与通过的电流I、用电器的电阻R之间的关系是P=I2R,下面说法正确的是( ) A.P为定值,I与R成反比例 B.P为定值,I2与R成反比例 C.P为定值,I与R成正比例 D.P为定值,I2与R成正比例 用小正方体搭一个几何体,使它的主视图和俯视图如图所示,这样的几何体最少需要正方体个数为( ) A.5 B.6 C.7 D.8 如图,F是平行四边形ABCD对角线BD上的点,BF:FD=1:3,则BE:EC=( ) 射击运动员射击一次,命中靶心”这个事件是( ) A.确定事件 B.必然事件 C.不可能事件 D.不确定事件 两个相似多边形一组对应边分别为3cm,4.5cm,那么它们的相似比为( ) 如图,点D在△ABC的边AC上,要判定△ADB与△ABC相似,添加一个条件,不正确的是( ). A.∠ABD=∠C B.∠ADB=∠ABC C. D. 下列语句正确的是( ) A.对角线互相垂直的四边形是菱形 B.有两边及一角对应相等的两个三角形全等 C.矩形的对角线相等 D.平行四边形是轴对称图形 如图,在平面直角坐标系中,点A坐标为(4,3),那么cosa的值是( ) A. B. C. D. 已知△ABC∽△DEF,若△ABC与△DEF的面积比为4:9,则△ABC与△DEF的周长比为( ) A.16:81 B.4:9 C.3:2 D.2:3 已知抛物线和直线l在同一直角坐标系中的图象如图,抛物线的对称轴为直线x=-1,P1(x1,y1)、P2(x2,y2)是抛物线上的点,P3(x3,y3)是直线l上的点,且-1<x1<x2,x3<﹣1,则y1、y2、y3的大小关系为( ) A.y1<y2<y3 B.y3<y1<y2 C.y3<y2<y1 D.y2<y1<y3 一 、填空题: 如图,要使ΔABC∽ΔACD,需补充的条件是 .(只要写出一种) 甲、乙两同学解方程x2+px+q=0,甲看错了一次项系数,解得根为4和-9;乙看错了常数项,解得根为2和3,则原方程为______________. 如图所示,已知点E在AC上,若点D在AB上,则满足条件 (只填一个条件),使△ADE与原△ABC相似. 如图,从y=ax2的图象上可以看出,当﹣1≤x≤2时,y的取值范围是 . 从﹣,﹣1,0,1这四个数中,任取一个数作为m的值,恰好使得关于x,y的二元一次方程组有整数解,且使以x为自变量的一次函数y=(m+1)x+3m﹣3的图象不经过第二象限,则取到满足条件的m值的概率为 . 已知点P在一次函数y=kx+b(k,b为常数,且k<0,b>0)的图象上,将点P向左平移1个单位,再向上平移2个单位得到点Q,点Q也在该函数y=kx+b的图象上. (1)k的值是 ; (2)如图,该一次函数的图象分别与x轴、y轴交于A,B两点,且与反比例函数y=图象交于C,D两点(点C在第二象限内),过点C作CE⊥x轴于点E,记S1为四边形CEOB的面积,S2为△OAB的面积,若=,则b的值是 . 二、解答题: 解方程:2x2﹣3x﹣1=0. 如图,Rt△ABC中,∠C=90°,AB=10,AC=8,E是AC上一点,AE=5,ED⊥AB于D. (1)求证:△ACB∽△ADE; (2)求AD的长度. 某学校对教室采用药薰消毒法进行消毒.已知药物燃烧时,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例,药物燃烧后,y与x成反比例(如图所示),现测得药物8min燃毕,此时室内空气中每立方米的含药量为6mg,请你根据题中所提供的信息,解答下列问题. (1)药物燃烧时y关于x的函数关系式为________,自变量x的取值范围是________;药物燃烧后y与x的函数关系式为________. (2)研究表明,当空气中每立方米的含药量低于1.6mg时学生可以进教室,那么从消毒开始,至少多少分钟后学生才能回到教室? (3)研究表明,当空气中每立方米的含药量不低于3mg且持续时间不低于10min时, 才能有效杀灭空气中的病菌, 那么此次消毒是否有效?为什么? 为响应国家的“一带一路”经济发展战略,树立品牌意识,我市质检部门对A、B、C、D四个厂家生产的同种型号的零件共2000件进行合格率检测,通过检测得出C厂家的合格率为95%,并根据检测数据绘制了如图1、图2两幅不完整的统计图. (1)抽查D厂家的零件为 件,扇形统计图中D厂家对应的圆心角为 ; (2)抽查C厂家的合格零件为 件,并将图1补充完整; (3)通过计算说明合格率排在前两名的是哪两个厂家; (4)若要从A、B、C、D四个厂家中,随机抽取两个厂家参加德国工业产品博览会,请用“列表法”或“画树形图”的方法求出(3)中两个厂家同时被选中的概率. 如图,某中学数学活动小组在学习了“利用三角函数测高”后.选定测量小河对岸一幢建筑物BC的高度.他们先在斜坡上的D处,测得建筑物顶的仰角为30°.且D离地面的高度DE=5m.坡底EA=10m,然后在A处测得建筑物顶B的仰角是50°,点E,A,C在同一水平线上,求建筑物BC的高.(结果保留整数) 随着铁路运量的不断增长,重庆火车北站越来越拥挤,为了满足铁路交通的快速发展,该火车站从去年开始启动了扩建工程,其中某项工程,甲队单独完成所需时间比乙队单独完成所需时间多5个月,并且两队单独完成所需时间的乘积恰好等于两队单独完成所需时间之和的6倍。 (1)求甲、乙队单独完成这项工程各需几个月? (2)若甲队每月的施工费为100万元,乙队每月的施工费比甲队多50万元,在保证工程质量的前提下,为了缩短工期,拟安排甲、乙两队分工合作完成这项工程。在完成这项工程中,甲队施工时间是乙队施工时间的2倍,那么,甲队最多施工几个月才能使工程款不超过1500万元?(甲、乙两队的施工时间按月取整数) 二、综合题: (1)如图1,正方形ABCD和CEFG的边长分别为m、n,用含m、n的代数式表示△AEG的面积。 (2)如图2,正方形ABCD和CEFG的边长分别为m、n,用含m、n的代数式表示△DBF的面积。 (3)如图,正方形ABCD、正方形CEFG和正方形MNHF的位置如图所示,点G在线段AN上,已知正方形CEFG的边长为6,则△AEN的面积为 (请直接写出结果,不需要过程) 如图,在平面直角坐标系中,O为原点,平行四边形ABCD的边BC在x轴上,D点在y轴上,C点坐标为(2,0),BC=6,∠BCD=60°,点E是AB上一点,AE=3EB,⊙P过D,O,C三点,抛物线y=ax2+bx+c过点D,B,C三点. (1)求抛物线的解析式; (2)求证:ED是⊙P的切线; (3)若将△ADE绕点D逆时针旋转90°,E点的对应点E′会落在抛物线y=ax2+bx+c上吗?请说明理由; (4)若点M为此抛物线的顶点,平面上是否存在点N,使得以点B,D,M,N为顶点的四边形为平行四边形?若存在,请直接写出点N的坐标;若不存在,请说明理由. 参考答案 1.A 2.B 3.B 4.C 5.A 6.D 7.A 8.C 9.C 10.D 11.D 12.D 13.略 14.答案为:x2-5x-36=0 15.答案为:∠B=∠AED; 16.答案为:0≤y≤4. 17.答案为:0.5 18.解:(1)设点P的坐标为(m,n),则点Q的坐标为(m﹣1,n+2), 依题意得:,解得:k=﹣2.故答案为:﹣2. (2)∵BO⊥x轴,CE⊥x轴,∴BO∥CE,∴△AOB∽△AEC. 又∵=,∴==. 令一次函数y=﹣2x+b中x=0,则y=b,∴BO=b; 令一次函数y=﹣2x+b中y=0,则0=﹣2x+b,解得:x=,即AO=. ∵△AOB∽△AEC,且=,∴. ∴AE=AO=b,CE=BO=b,OE=AE﹣AO=b. ∵OE•CE=|﹣4|=4,即b2=4,解得:b=3,或b=﹣3(舍去).故答案为:3. 19.解:2x2﹣3x﹣1=0,a=2,b=﹣3,c=﹣1,∴△=9+8=17,∴x=,x1=,x2=. 20.1)证明:∵DE⊥AB,∠C=90°,∴∠EDA=∠C=90°,∵∠A=∠A,∴△ACB∽△ADE; (2)解:∵△ACB∽△ADE,∴=,∴=,∴AD=4. 21.解:(1)y=0.45x,0≤x≤8,y=48x-1;(2)30分钟;(3)有效(此次消毒时间可持续12分钟). 22.解:(1)D厂的零件比例=1﹣20%﹣20%﹣35%=25%, D厂的零件数=2000×25%=500件;D厂家对应的圆心角为360°×25%=90°; (2)C厂的零件数=2000×20%=400件,C厂的合格零件数=400×95%=380件, 如图: (3)A厂家合格率=630÷(2000×35%)=90%,B厂家合格率=370÷(2000×20%)=92.5%, C厂家合格率=95%,D厂家合格率470÷500=94%,合格率排在前两名的是C、D两个厂家; (4)根据题意画树形图如下: 共有12种情况,选中C、D的有2种,则P(选中C、D)==. 23.解:过点D作DM⊥BC于点M,DN⊥AC于点N,如图所示: 则四边形DMCN是矩形,DH=EC,DE=HC,设建筑物BC的高度为xm,则BH=(x﹣5)m, 在Rt△DHB中,∠BDH=30°,∴DH=(x﹣5),AC=EC﹣EA=(x﹣5)﹣10, 在Rt△ACB中,∠BAC=50°,tan∠BAC=,∴x=tan50°•[(x﹣5)], 解得:x≈21,答:建筑物BC的高约为21m. 24.解:(1) 设乙队单独完成这项工程需x个月,则甲队单独完成这项工程需x+5个月, 根据题意,得,即, 解得(不合题意,舍去)。∴。 答:甲队单独完成这项工程需15个月,乙队单独完成这项工程需10个月。 (2)设甲队的施工时间为y个月,则乙队的施工时间为个月, 根据题意,得, 解得。 答:甲队最多施工12个月才能使工程款不超过1500万元。 25.答案为:(1)0.5n2;(2)0.5m2;(3)36. 26.解:(1)∵C(2,0),BC=6,∴B(﹣4,0), 在Rt△OCD中,∵tan∠OCD=,∴OD=2tan60°=2,∴D(0,2), 21cnjy.com 设抛物线的解析式为y=a(x+4)(x﹣2), 把D(0,2)代入得a4(﹣2)=2,解得a=﹣, ∴抛物线的解析式为y=﹣(x+4)(x﹣2)=﹣x2﹣x+2; (2)在Rt△OCD中,CD=2OC=4,∵四边形ABCD为平行四边形, ∴AB=CD=4,AB∥CD,∠A=∠BCD=60°,AD=BC=6, ∵AE=3BE,∴AE=3,∴=,==,∴=, 而∠DAE=∠DCB, ∴△AED∽△COD, ∴∠ADE=∠CDO, 而∠ADE+∠ODE=90°∴∠CDO+∠ODE=90°,∴CD⊥DE, ∵∠DOC=90°,∴CD为⊙P的直径,∴ED是⊙P的切线; (3)E点的对应点E′不会落在抛物线y=ax2+bx+c上.理由如下: ∵△AED∽△COD,∴=,即=,解得DE=3, ∵∠CDE=90°,DE>DC, ∴△ADE绕点D逆时针旋转90°,E点的对应点E′在射线DC上, 而点C、D在抛物线上,∴点E′不能在抛物线上; (4)存在. ∵y=﹣x2﹣x+2=﹣(x+1)2+ ∴M(﹣1,), 而B(﹣4,0),D(0,2),如图2,当BM为平行四边形BDMN的对角线时,点D向左平移4个单位,再向下平移2个单位得到点B,则点M(﹣1,)向左平移4个单位,再向下平移2个单位得到点N1(﹣5,); 【来源:21·世纪·教育·网】 当DM为平行四边形BDMN的对角线时,点B向右平移3个单位,再向上平移个单位得到点M,则点D(0,2)向右平移3个单位,再向上平移个单位得到点N2(3,) 【出处:21教育名师】 当BD为平行四边形BDMN的对角线时,点M向左平移3个单位,再向下平移个单位得到点B,则点D(0,2)向右平移3个单位,再向下平移个单位得到点N3(﹣3,﹣),综上所述,点N的坐标为(﹣5,)、(3,)、(﹣3,﹣). 查看更多