中考复习专题相似三角形一线三等角

中考复习专题相似三角形一线三等角

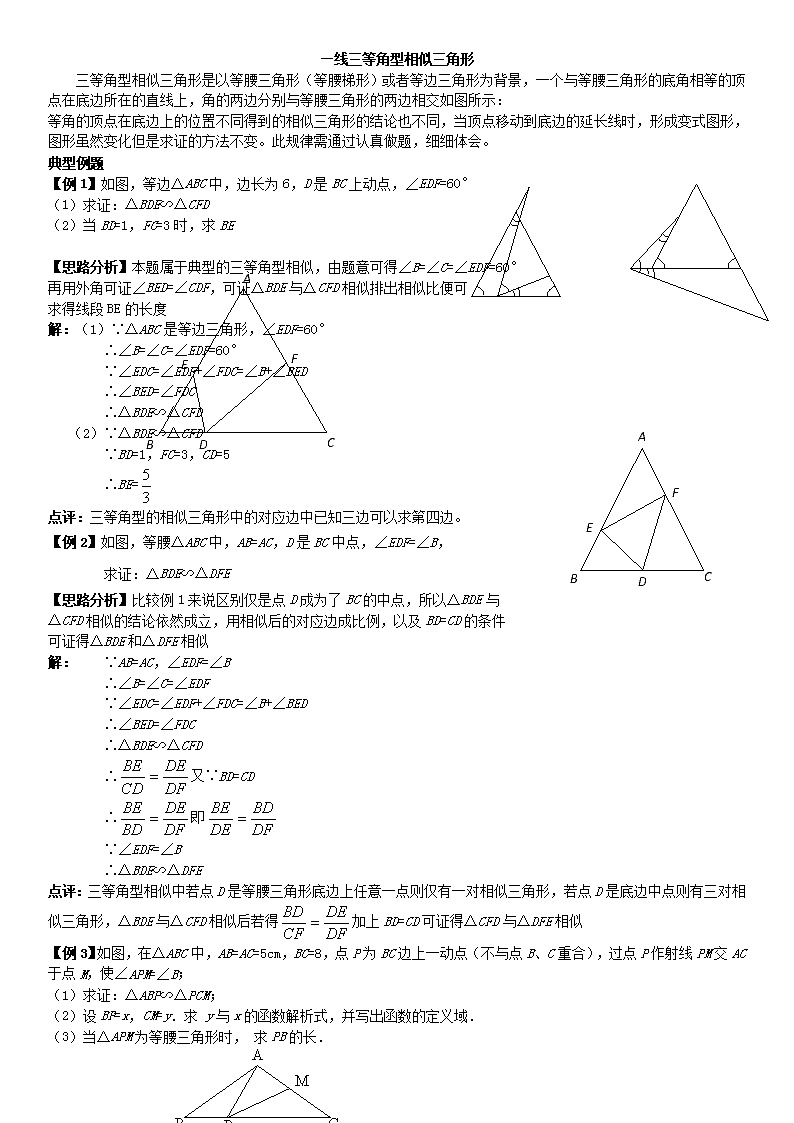
‎—线三等角型相似三角形 三等角型相似三角形是以等腰三角形（等腰梯形）或者等边三角形为背景，一个与等腰三角形的底角相等的顶点在底边所在的直线上，角的两边分别与等腰三角形的两边相交如图所示：‎ 等角的顶点在底边上的位置不同得到的相似三角形的结论也不同，当顶点移动到底边的延长线时，形成变式图形，图形虽然变化但是求证的方法不变。此规律需通过认真做题，细细体会。‎ 典型例题 ‎【例1】如图，等边△ABC中，边长为6，D是BC上动点，∠EDF=60°‎ ‎（1）求证：△BDE∽△CFD ‎（2）当BD=1，FC=3时，求BE ‎ C A D B E F ‎【思路分析】本题属于典型的三等角型相似，由题意可得∠B=∠C=∠EDF=60°‎ 再用外角可证∠BED=∠CDF，可证△BDE与△CFD相似排出相似比便可 求得线段BE的长度 解：（1）∵△ABC是等边三角形，∠EDF=60°‎ ‎∴∠B=∠C=∠EDF=60°‎ ‎∵∠EDC=∠EDF+∠FDC=∠B+∠BED ‎∴∠BED=∠FDC C D E A B F ‎∴△BDE∽△CFD ‎（2）∵△BDE∽△CFD ‎∵BD=1，FC=3，CD=5‎ ‎∴BE=‎ 点评：三等角型的相似三角形中的对应边中已知三边可以求第四边。‎ ‎【例2】如图，等腰△ABC中，AB=AC，D是BC中点，∠EDF=∠B，‎ 求证：△BDE∽△DFE ‎【思路分析】比较例1来说区别仅是点D成为了BC的中点，所以△BDE与 ‎△CFD相似的结论依然成立，用相似后的对应边成比例，以及BD=CD的条件 可证得△BDE和△DFE相似 解： ∵AB=AC，∠EDF=∠B ‎∴∠B=∠C=∠EDF ‎∵∠EDC=∠EDF+∠FDC=∠B+∠BED ‎∴∠BED=∠FDC ‎∴△BDE∽△CFD ‎ ∴又∵BD=CD ‎∴即 ‎ ∵∠EDF=∠B ‎∴△BDE∽△DFE 点评：三等角型相似中若点D是等腰三角形底边上任意一点则仅有一对相似三角形，若点D是底边中点则有三对相似三角形，△BDE与△CFD相似后若得加上BD=CD可证得△CFD与△DFE相似 ‎【例3】如图，在△ABC中，AB=AC=5cm，BC=8，点P为BC边上一动点（不与点B、C重合），过点P作射线PM交AC于点M，使∠APM=∠B；‎ ‎（1）求证：△ABP∽△PCM；‎ ‎（2）设BP=x，CM=y．求 y与x的函数解析式，并写出函数的定义域．‎ ‎（3）当△APM为等腰三角形时， 求PB的长．‎ A B P C M ‎【思路分析】第（1）（2）小题都是用常规的三等角型相似的方法。对△APM 进行等腰三角形的分类讨论时，可将条件转化成与△ABP∽△PCM相关的结论 A B C P M 解：（1）∵AB=AC，∠APM=∠B∴∠APM=∠B=∠C ‎∵∠APC=∠APM+∠MPC=∠B+∠BAP ‎∴∠BAP=∠MPC ‎∴△ABP∽△PCM ‎（2）∵BP=x，CM=y，CP=8-x A B C P M ‎∵‎ ‎（3）当AP=PM时 ‎∵∴PC=AB=5‎ ‎∴BP=3‎ 当AP=AM时 ‎∵∠APM=∠B=∠C ‎∴∠PAM=∠BAC即点P与点B重合 ‎∴P不与点B、C重合 ‎∴舍去 当MP=AM时 ‎∴∠MAP=∠MPA ‎∴△MAP∽△ABC ‎∴即 ‎∴BP=‎ 点评：等腰三角形分类讨论需要灵活应用，可采用的方法添底边上的高，将等腰的条件进行转化，三等角型相似这类问题中可将等腰的条件转化至△ABP和△PCM中简化运算。‎ ‎【例4】（1）在中，，，点、分别在射线、上（点不与点、点重合），且保持.‎ ‎①若点在线段上（如图10），且，求线段的长；‎ ‎②若，，求与之间的函数关系式，并写出函数的 ‎ 定义域；‎ ‎（2）正方形的边长为（如图12），点、分别在直线、上（点不与点、点重合），且保持.‎ 当时，写出线段的长（不需要计算过程，请直接写出结果）.‎ A B C D 图12‎ A B C P Q A B C 备用图 ‎【思路分析】‎ 本例与前几例的区别在于与等腰三角形底角相等的角的顶点不仅在线段上还可以运动至线段的延长线上，这类变式问题是上海中考中最常见的，虽然图形改变，但是方法不变，依旧是原来的两个三角形相似列出比例式后求解。当等腰三角形变式为正方形时，依然沿用刚才的方法便可破解此类问题。‎ 解：（1）∵，，‎ 又∵，∴.‎ A B C 备用图 P Q ‎∴，.‎ ‎（2）若点在线段上，由（1）知.‎ 又∵，，∴ ，即.‎ 故所求的函数关系式为，.‎ 若点在线段的延长线上，如图11.‎ 又∵，‎ ‎∴ ，即 .‎ ‎（2）当点在线段上，，或.‎ 当点在线段的延长线上，则点在线段的延长线上，.‎ 当点在线段的延长线上，则点在线段的延长线上，.‎ 点评：此题是典型的图形变式题，记住口诀：“图形改变，方法不变”。动点在线段上时，通过哪两个三角形相似求解，当动点在线段的延长线上时，还是找原来的两个三角形，多数情况下这两个三角形还是相似的，还是可以沿用原来的方法求解。‎ 强化训练：‎ 1. 如图，在△ABC中，，，是边上的一个动点，点在边上，且．‎ ‎(1) 求证：△ABD∽△DCE；‎ ‎(2) 如果，，求与的函数解析式，并写出自变量的定义域；‎ ‎(3) 当点是的中点时，试说明△ADE是什么三角形，并说明理由．‎ A B C D E 2. 已知：如图，在△ABC中，，，点D在边AB上，，点E在边BC上．又点F在边AC上，且．‎ ‎(1) 求证：△FCE∽△EBD；‎ ‎(2) 当点D在线段AB上运动时，是否有可能使．‎ 如果有可能，那么求出BD的长．如果不可能请说明理由．‎ A B C D E F C P E A B D 3. 如图，在△ABC中，AB=AC=5，BC=6，P是BC上一点，且BP=2，将一个大小与∠B相等的角的顶点放在P ‎ 点，然后将这个角绕P点转动，使角的两边始终分别与AB、AC相交，交点为D、E。‎ ‎（1）求证△BPD∽△CEP ‎（2）是否存在这样的位置，△PDE为直角三角形？‎ 若存在，求出BD的长；若不存在，说明理由。‎ 1. 如图，在△ABC中，AB=AC=5，BC=6，P是BC上的一个动点(与B、C不重合)，PE⊥AB与E，PF⊥BC交AC与F，设PC=x，记PE=，PF=‎ ‎（1）分别求、关于x的函数关系式 ‎（2）△PEF能为直角三角形吗?若能，求出CP的长，若不能，请说明理由。‎ C P E A B F 2. 如图，在△ABC中，AB=AC=5，BC=6，P是BC上的一个动点(与B、C不重合)，PE⊥AB与E，PF⊥BC交AC与F，设PC=x，△PEF的面积为y ‎（1）写出图中的相似三角形不必证明；‎ C P E A B F ‎（2）求y与x的函数关系式，并写出x的取值范围；‎ ‎（3）若△PEF为等腰三角形，求PC的长。‎ 3. 已知在等腰三角形中，，是的中点， 是上的动点（不与、重合），连结，过点作射线，使，射线交射线于点，交射线于点.‎ ‎（1）求证：∽；‎ ‎（2）设.‎ ‎①用含的代数式表示；‎ ‎②求关于的函数解析式，并写出的定义域.‎ 4. 已知在梯形ABCD中，AD∥BC，AD＜BC，且AD＝5，AB＝DC＝2．‎ ‎（1）如图8，P为AD上的一点，满足∠BPC＝∠A．‎ ‎①求证；△ABP∽△DPC ‎②求AP的长．‎ ‎（2）如果点P在AD边上移动（点P与点A、D不重合），且满足∠BPE＝∠A，PE交直线BC于点E，同时交直线DC于点Q，那么 ‎①当点Q在线段DC的延长线上时，设AP＝x，CQ＝y，求y关于x的函数解析式，并写出函数的定义域；‎ ‎②当CE＝1时，写出AP的长（不必写出解题过程）．‎ C D A B P 5. 已知：如图，直角梯形ABCD中，AD∥BC，，，，，AM∥DC，E、F分别是线段AD、AM上的动点（点E与A、D不重合）且，设 ‎（1）求证：；‎ ‎（2）求与的函数关系式并写出定义域；‎ ‎（3）若点E在边AD上移动时， 为等腰三角形，求的值；‎ A E F D B M C 1. 已知在梯形ABCD中，AD∥BC，AD＜BC，且BC =6，AB=DC=4，点E是AB的中点．‎ ‎ （1）如图，P为BC上的一点，且BP=2．求证：△BEP∽△CPD；‎ ‎ （2）如果点P在BC边上移动（点P与点B、C不重合），且满足∠EPF=∠C，PF交直线CD于点F，同时交直线AD于点M，那么 ‎ ①当点F在线段CD的延长线上时，设BP=，DF=，求关于的函数解析式，并写出函数的定义域；②当时，求BP的长．‎ E D C B A ‎（备用图）‎ E D C B A P ‎（第25题图）‎ 2. 如图，在梯形ABCD中，AD//BC，AB=CD=BC=4，AD=2．点M为边BC的中点，以M为顶点作∠EMF=∠B，射线ME交边AB于点E，射线MF交边CD于点F，连结EF．‎ ‎（1）指出图中所有与△BEM相似的三角形，并加以证明；‎ ‎（2）设BE=x，CF=y，求y关于x的函数解析式，并写出定义域；‎ A B C D M E F 答案：‎ 1. 解：（1）∵AB=AC∴∠B=∠C ‎∵∠ADC=∠ADE+∠CDE=∠B+∠BAD∴∠BAD=∠CDE∴△ABD∽△DCE ‎（2）∵△ABD∽△DCE∴‎ ‎（3）∵，是的中点∴AD⊥BC∴∠DAE+∠ADE=90°∵‎ ‎∴△ADE是直角三角形 2. 解：（1）∵AB=AC∴∠B=∠C ‎∵∠BED+∠DEF=∠C+∠EFC=90°又∵∴∠BED=∠EFC ‎∴△FCE∽△EBD ‎（2）∵BD=x，BE=，‎ ‎∵△FCE∽△EBD∴若∴∴‎ ‎∴∴BD不存在 3. 解：（1）∵AB=AC∴∠B=∠C C P E A B D H ‎∵∠DPC=∠DPE+∠EPC=∠B+∠BDP∴∠EPC =∠BDP ∴△ABD∽△DCE C P E A B D H ‎（2）∵∠DPE=∠B90°‎ 若∠PDE=90°，在Rt△ABH和Rt△PDE中 ‎ ∴cos∠ABH=cos∠DPE=∴‎ ‎∵PC=4 ∴‎ 若∠PED=90°在Rt△ABH和Rt△PDE中 ‎ ∴cos∠ABH=cos∠PED=∴‎ ‎∵PC=4 ∴（舍去）‎ C P E A B F H 综上所述，BD的长为 1. 解：（1）、 ‎ ‎（2）∵∠FPE=∠B90°‎ 若∠PFE=90°，在Rt△ABH和Rt△PFE中 ‎ ∴cos∠ABH=cos∠FPE=∴∴∴‎ C P E A B F H 若∠PEF=90°，在Rt△ABH和Rt△PFE中 ‎ ∴cos∠ABH=cos∠FPE=‎ 2. 解：（1）△PEB∽△EPC C P E A B F G H M ‎（2）∵PC=x∴，，‎ 即 ‎（3）当PE=PF时，△EPC≌△PEB，PC=BE=x，∴‎ 当PE=EF时，，cos∠EPH=cosB，∴‎ 当FE=PF时，， cos∠FPM=cosB，∴‎ 综上所述，PC的长分别为、、‎ 3. 解：（1）∵,∴∵‎ 又,∴∽ ‎ ‎（2）①∵∽，∴‎ ‎∵是的中点，，∴，又 ∵‎ ‎∴当点在线段的延长线上时，，∴ ‎ 当点在线段上时，，∴‎ ‎②过点作DG∥AB,交于点 ‎ ‎∴当点在线段的延长线上时，∴，∴∴‎ 当点在线段上时，∴，∴ ∴ ‎ 1. 解：（1）①证明：∵ ∠ABP＝180°－∠A－∠APB，∠DPC＝180°－∠BPC－∠APB，‎ ‎∠BPC＝∠A，∴ ∠ABP＝∠DPC．‎ ‎∵ 在梯形ABCD中，AD∥BC，AB＝CD，∴ ∠A＝∠D．∴ △ABP∽△DPC．‎ ‎②解：设AP＝x，则DP＝5－x，由△ABP∽△DPC，得，即 解得x1＝1，x2＝4，则AP的长为1或4．‎ ‎（2）①解：类似（1）①，易得△ABP∽△DPQ，∴ ‎ C D A B P Q E 即，得，1＜x＜4．‎ ‎②AP＝2或AP＝3－．‎ 2. 证明：（1）过点M作交于G ‎∵AD//BC，AB//MG ∴AG=BM=6‎ ‎∵AD=12 ∴AG=GD∴≌∴AM=DM ‎(2) ∵ ∴∴‎ ‎∴定义域为：‎ ‎(3) ∵∴EM≠FM ‎∴若为等腰三角形，则EF=EM或EF=FM ‎① 当EF=EM时,12-=10∴=2‎ ‎②当EF=FM时∵∴AE=EM∴∴‎ 3. 证明：（1）∵在梯形ABCD中，AD∥BC，AB=DC，∴∠B=∠C ‎ BE=2,BP=2,CP=4,CD=4，∴，∴△BEP∽△CPD ‎ ‎(2)①又∠EPF=∠C=∠B，∴‎ ‎∴△BEP∽△CPF，∴∴‎ ‎②当点F在线段CD的延长线上时 ‎∠FDM=∠C=∠B， ，∴△BEP∽△DMF ‎ 又，∴，Δ＜0，∴此方程无实数根，‎ 故当点F在线段CD的延长线上时，不存在点P使 当点F在线段CD上时，同理△BEP∽△DMF ‎，∴，又∴△BEP∽△CPF∴，∴‎ ‎∴，∴，解得 ，‎ 由于不合题意舍去，∴，即BP=1‎ 所以当时，BP的长为1．‎ 1. 解：（1）△CMF∽△BEM，△MEF∽△BEM．‎ 证明如下：在梯形ABCD中，∵AD∥BC，AB=CD，∴∠B=∠C．‎ 又∵∠EMF+∠FMC=∠B+∠BEM，∠EMF=∠B，∴∠FMC=∠BEM．‎ ‎∴△CMF∽△BEM． ∴． ‎ 又∵CM=BM，∴．∵∠EMF=∠B，∴△MEF∽△BEM．‎ ‎（2）∵△CMF∽△BEM，∴．‎ ‎∵BM=CM=2，∴．∴所求函数的解析式为，（）‎