- 2021-05-10 发布 |
- 37.5 KB |
- 15页


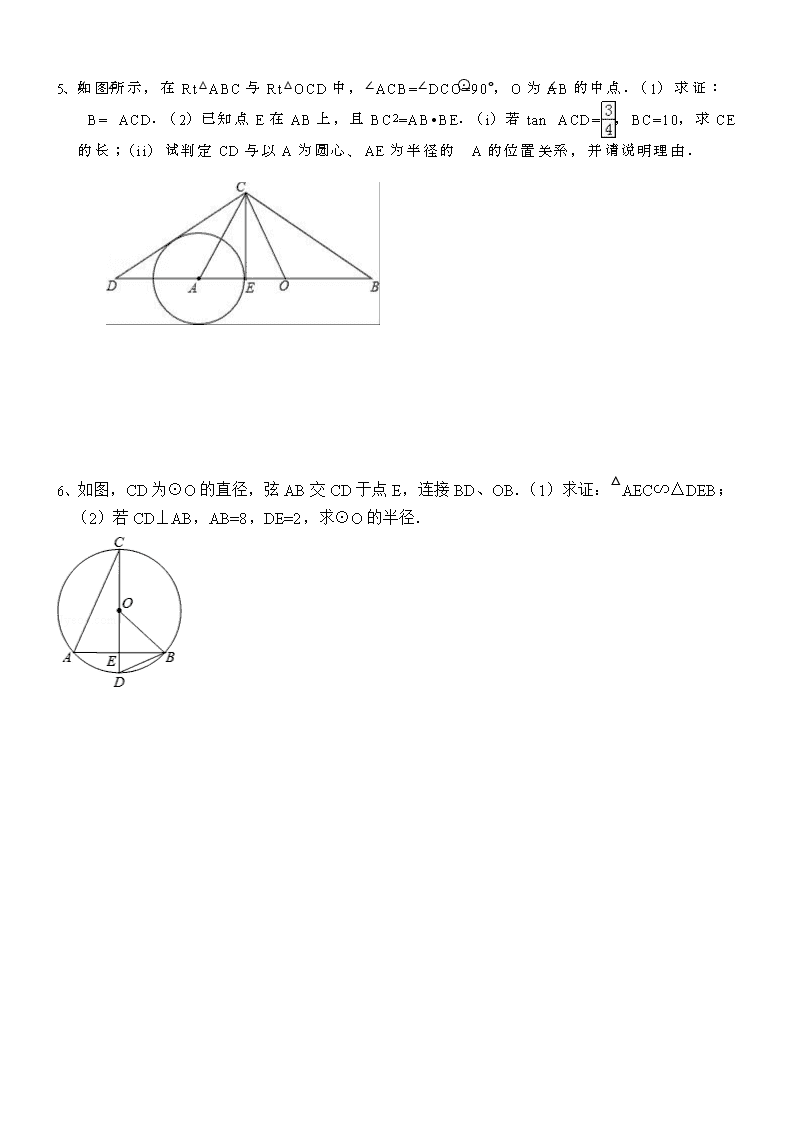
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
中考数学圆习题
中考数学圆习题 1、如图,AB是⊙O的弦,BC切⊙O于点B,AD⊥BC,垂足为D,OA是⊙O的半径,且OA=3. (1)求证:AB平分∠OAD;(2)若点E是优弧上一点,且∠AEB=60°,求扇形OAB的面积.(计算结果保留π) 2、如图,在Rt△ABC中,∠ACB=90°,以BC为直径的⊙O交AB于点D,E是AC的中点,OE交CD于点F.(1)若∠BCD=36°,BC=10,求BD的长;(2)判断直线DE与⊙O的位置关系,并说明理由;(3)求证:2CE2=AB•EF. 3、在等腰△ABC中,AC=BC,以BC为直径的⊙O分别与AB,AC相交于点D,E,过点D作DF⊥AC,垂足为 点F.(1)求证:DF是⊙O的切线;(2)分别延长CB,FD,相交于点G,∠A=60°,⊙O的半径为6,求阴影部分的面积. 4、如图,已知⊙O是△ABC的外接圆,AD是⊙O的直径,且BD=BC,延长AD到E,且有∠EBD=∠CAB. (1)求证:BE是⊙O的切线;(2)若BC=,AC=5,求圆的直径AD及切线BE的长. 5、如图所示,在Rt△ABC与Rt△OCD中,∠ACB=∠DCO=90°,O为AB的中点.(1)求证:∠B=∠ACD.(2)已知点E在AB上,且BC2=AB•BE.(i)若tan∠ACD=,BC=10,求CE的长;(ii)试判定CD与以A为圆心、AE为半径的⊙A的位置关系,并请说明理由. 6、如图,CD为⊙O的直径,弦AB交CD于点E,连接BD、OB.(1)求证:△AEC∽△DEB; (2)若CD⊥AB,AB=8,DE=2,求⊙O的半径. 7、如图,△ABC是⊙O的内接三角形,AB为直径,过点B的切线与AC的延长线交于点D,E是BD中点,连接CE.(1)求证:CE是⊙O的切线;(2)若AC=4,BC=2,求BD和CE的长. 8、如图,AB是⊙O的直径,C是⊙O上的一点,直线MN经过点C,过点A作直线MN的垂线,垂足为点D,且∠BAC=∠CAD.(1)求证:直线MN是⊙O的切线;(2)若CD=3,∠CAD=30°,求⊙O的半径. 9、如图,OA,OD是⊙O半径,过A作⊙O的切线,交∠AOD的平分线于点C,连接CD,延长AO交⊙O于点E,交CD的延长线于点B(1)求证:直线CD是⊙O的切线;(2)如果D点是BC的中点,⊙O的半径为3cm,求的长度(结果保留π) 10、在平面直角坐标中,△ABC三个顶点坐标为A(﹣,0)、B(,0)、C(0,3). (1)求△ABC内切圆⊙D的半径.(2)过点E(0,﹣1)的直线与⊙D相切于点F(点F在第一象限),求直线EF的解析式.(3)以(2)为条件,P为直线EF上一点,以P为圆心,以2为半径作⊙P.若⊙P上存在一点到△ABC三个顶点的距离相等,求此时圆心P的坐标. 11、如图,四边形ABCD内接于⊙O,对角线AC为⊙O的直径,过点C作AC的垂线交AD的延长线于点E,点F为CE的中点,连接DB,DC,DF. (1)求∠CDE的度数;(2)求证:DF是⊙O的切线;(3)若AC=2DE,求tan∠ABD的值. 12、如图,P为正方形ABCD的边BC上一动点(P与B、C不重合),连接AP,过点B作BQ⊥AP交CD于 点Q,将△BQC沿BQ所在的直线对折得到△BQC′,延长QC′交BA的延长线于点M.(1)试探究AP与BQ的数量关系,并证明你的结论;(2)当AB=3,BP=2PC,求QM的长;(3)当BP=m,PC=n时,求AM的长. 13、已知如图,以Rt△ABC的AC边为直径作⊙O交斜边AB于点E,连接EO并延长交BC的延长线于点D,点F为BC的中点,连接EF.(1)求证:EF是⊙O的切线;(2)若⊙O的半径为3,∠EAC=60°,求AD的长. 14、如图,AB是⊙O的直径,点C、D为半圆O的三等分点,过点C作CE⊥AD,交AD的延长线于点E. (1)求证:CE是⊙O的切线;(2)判断四边形AOCD是否为菱形?并说明理由. 15、如图,在直角坐标系中,⊙M经过原点O(0,0),点A(,0)与点B(0,﹣),点D在劣弧上,连接BD交x轴于点C,且∠COD=∠CBO.(1)求⊙M的半径;(2)求证:BD平分∠ABO;(3)在线段BD的延长线上找一点E,使得直线AE恰好为⊙M的切线,求此时点E的坐标. 16、如图,已知△ABC内接于⊙O,且AB=AC,直径AD交BC于点E,F是OE上的一点,使CF∥BD. (1)求证:BE=CE;(2)试判断四边形BFCD的形状,并说明理由;(3)若BC=8,AD=10,求CD的长. 17、如图,已知⊙O的直径为AB,AC⊥AB于点A,BC与⊙O相交于点D,在AC上取一点E,使得ED=EA. (1)求证:ED是⊙O的切线.(2)当OA=3,AE=4时,求BC的长度. 18、如图,E是长方形ABCD的边AB上的点,EF⊥DE交BC于点F;(1)求证:△ADE∽△BEF;(2)设H是ED上一点,以EH为直径作⊙O,DF与⊙O相切于点G,若DH=OH=3,求图中阴影部分的面积(结果保留到小数点后面第一位,≈1.73,π≈3.14). 19、如图,点A是⊙O上一点,OA⊥AB,且OA=1,AB=,OB交⊙O于点D,作AC⊥OB,垂足为M,并交⊙O于点C,连接BC.(1)求证:BC是⊙O的切线;(2)过点B作BP⊥OB,交OA的延长线于点P,连接PD,求sin∠BPD的值. 中考数学圆习题答案 1、(1)证明:连接OB,如图所示:∵BC切⊙O于点B, ∴OB⊥BC,∵AD⊥BC,∴AD∥OB,∴∠DAB=∠OBA, ∵OA=OB,∴∠OAB=∠OBA,∴∠DAB=∠OAB, ∴AB平分∠OAD; (2)解:∵点E是优弧上一点,且∠AEB=60°, ∴∠AOB=2∠AEB=120°,∴扇形OAB的面积==3π. 2、解:(1)∵BC是直径,∴∠BDC=90°, 在Rt△BCD中,∵BC=10,∠BCD=36°,∴BD=BC•sin36°=10•sin36°≈5.9. (2)连接OD.∵AE=EC,OB=OC,∴OE∥AB,∵CD⊥AB, ∴OE⊥CD,∵OD=OC,∴∠DOE=∠COE,在△EOD和△EOC中, ∴△EOD≌△EOC,∴∠EDO=∠ECO=90°,∴OD⊥DE, ∴DE是⊙O的切线. (3)∵OE⊥CD,∴DF=CF,∵AE=EC,∴AD=2EF, ∵∠CAD=∠CAB,∠ADC=∠ACB=90°,∴△ACD∽△ABC, ∴AC2=AD•AB,∵AC=2CE,∴4CE2=2EF•AB,∴2CE2=EF•AB. 3、⑴连接OD,CD,∵BC是⊙O的直径∴∠BDC=90°即CD⊥AB ∵AC=BC∴CD平分AB,即点D是AB的中点 又∵点O是BC的中点 ∴OD∥AC 又∵DF⊥AC∴DF⊥OD 又∵OD是⊙O的半径 ∴DF是⊙O的切线 (2)∠A=600,AC=BC ∴∠OBD=∠A=600 ∵OD=OB ∴△BOD为等边三角形 ∴∠BOD=600 ∵⊙O的半径为6 ∴OD=6 ∵DF是⊙O的切线 ∴∠ODG=900 ∴tan600= 即:DG=tan600·OD= ∴S阴影=S△ODG-S扇形BOD = = = 4、解:如图,连接OB,∵BD=BC,∴∠CAB=∠BAD,∵∠EBD=∠CAB, ∴∠BAD=∠EBD,∵AD是⊙O的直径,∴∠ABD=90°,OA=BO, ∴∠BAD=∠ABO,∴∠EBD=∠ABO, ∴∠OBE=∠EBD+∠OBD=∠ABD+∠OBD=∠ABD=90°,∵点B在⊙O上, ∴BE是⊙O的切线, (2)如图2,设圆的半径为R,连接CD,∵AD为⊙O的直径,∴∠ACCD=90°, ∵BC=BD,∴OB⊥CD,∴OB∥AC,∵OA=OD,∴OF=AC=, ∵四边形ACBD是圆内接四边形,∴∠BDE=∠ACB, ∵∠DBE=∠ACB, ∴△DBE∽△CAB, ∴, ∴, ∴DE=, ∵∠OBE=∠OFD=90°,∴DF∥BE,∴,∴,∵R>0,∴R=3, ∴AB== ∵=, ∴BE=. 5、解:(1)∵∠ACB=∠DCO=90°,∴∠ACB﹣∠ACO=∠DCO﹣∠ACO, 即∠ACD=∠OCB,又∵点O是AB的中点,∴OC=OB,∴∠OCB=∠B, ∴∠ACD=∠B, (2)(i)∵BC2=AB•BE,∴=,∵∠B=∠B,∴△ABC∽△CBE, ∴∠ACB=∠CEB=90°,∵∠ACD=∠B, ∴tan∠ACD=tan∠B=, 设BE=4x,CE=3x,由勾股定理可知:BE2+CE2=BC2, ∴(4x)2+(3x)2=100,∴解得x=2,∴CE=6; (ii)过点A作AF⊥CD于点F,∵∠CEB=90°, ∴∠B+∠ECB=90°,∵∠ACE+∠ECB=90°,∴∠B=∠ACE, ∵∠ACD=∠B,∴∠ACD=∠ACE,∴CA平分∠DCE, ∵AF⊥CE,AE⊥CE,∴AF=AE,∴直线CD与⊙A相切. 6、(1)证明:∵∠AEC=∠DEB,∠ACE=∠DBE,∴△AEC∽△DEB. (2)解:设⊙O的半径为r,则CE=2r﹣2.∵CD⊥AB,AB=8, ∴AE=BE=AB=4.∵△AEC∽△DEB,∴,即, 解得:r=5. 7、(1)证明:连接OC,如图所示:∵BD是⊙O的切线, ∴∠CBE=∠A,∠ABD=90°,∵AB是⊙O的直径, ∴∠ACB=90°,∴∠ACO+∠BCO=90°,∠BCD=90°, ∵E是BD中点,∴CE=BD=BE,∴∠BCE=∠CBE=∠A, ∵OA=OC,∴∠ACO=∠A,∴∠ACO=∠BCE, ∴∠BCE+∠BCO=90°,即∠OCE=90°,CE⊥OC, ∴CE是⊙O的切线; (2)解:∵∠ACB=90°,∴AB===2, ∵tanA====,∴BD=AB=,∴CE=BD=. 8、(1)证明:连接OC,因为OA=OC,所以∠BAC=∠ACO. 因为AC平分∠BAD,所以∠BAC=∠CAD,故∠ACO=∠CAD. 所以OC∥AD,又已知AD丄MN,所以OC丄MN, 所以,直线MN是⊙O的切线; (2)解:已知AB是⊙O的直径,则∠ACB=90°,又AD丄MN, 则∠ADC=90°.因为CD=3,∠CAD=30°, 所以AD=3,AB=6 在Rt△ABC和Rt△ACD中,∠BAC=∠CAD, 所以Rt△ABC∽Rt△ACD,则, 则AB=4,所以⊙O的半径为2. 9、(1)证明:∵AC是⊙O切线,∴OA⊥AC,∴∠OAC=90°,∵CO平分∠AOD, ∴∠AOC=∠COD,在△AOC和△DOC中, ,∴△AOC≌△DOC,∴∠ODC=∠OAC=90°,∴OD⊥CD,∴直线CD是⊙O的切线. (2)∵OD⊥BC,DC=DB,∴OC=OB,∴∠OCD=∠B=∠ACO,∵∠B+∠ACB=90°,∴∠B=30°,∠DOE=60°, ∴的长==π. 10、解:(1)连接BD,∵B(,0),C(0,3),∴OB=,OC=3, ∴tan∠CBO==,∴∠CBO=60°∵点D是△ABC的内心, ∴BD平分∠CBO,∴∠DBO=30°,∴tan∠DBO=, ∴OD=1,∴△ABC内切圆⊙D的半径为1; (2)连接DF,过点F作FG⊥y轴于点G,∵E(0,﹣1) ∴OE=1,DE=2,∵直线EF与⊙D相切,∴∠DFE=90°,DF=1, ∴sin∠DEF=,∴∠DEF=30°,∴∠GDF=60°,∴在Rt△DGF中, ∠DFG=30°,∴DG=,由勾股定理可求得:GF=,∴F(,), 设直线EF的解析式为:y=kx+b, ∴,∴直线EF的解析式为:y=x﹣1; (3)∵⊙P上存在一点到△ABC三个顶点的距离相等, ∴该点必为△ABC外接圆的圆心,由(1)可知:△ABC是等边三角形, ∴△ABC外接圆的圆心为点D∴DP=2, 设直线EF与x轴交于点H,∴令y=0代入y=x﹣1, ∴x=,∴H(,0),∴FH=, 当P在x轴上方时,过点P1作P1M⊥x轴于M, 由勾股定理可求得:P1F=3,∴P1H=P1F+FH=, ∵∠DEF=∠HP1M=30°,∴HM=P1H=,P1M=5, ∴OM=2,∴P1(2,5), 当P在x轴下方时,过点P2作P2N⊥x轴于点N, 由勾股定理可求得:P2F=3,∴P2H=P2F﹣FH=, ∴∠DEF=30°∴∠OHE=60°∴sin∠OHE=, ∴P2N=4,令y=﹣4代入y=x﹣1,∴x=﹣, ∴P2(﹣,﹣4), 综上所述,若⊙P上存在一点到△ABC三个顶点的距离相等,此时圆心P的坐标为(2,5)或(﹣,﹣4). 11、(1)解:∵对角线AC为⊙O的直径, ∴∠ADC=90°,∴∠EDC=90°; (2)证明:连接DO,∵∠EDC=90°,F是EC的中点,∴DF=FC, ∴∠FDC=∠FCD,∵OD=OC,∴∠OCD=∠ODC,∵∠OCF=90°, ∴∠ODF=∠ODC+∠FDC=∠OCD+∠DCF=90°,∴DF是⊙O的切线; (3)解:如图所示:可得∠ABD=∠ACD∵∠E+∠DCE=90°,∠DCA+∠DCE=90°, ∴∠DCA=∠E,又∵∠ADC=∠CDE=90°,∴△CDE∽△ADC, ∴=,∴DC2=ADDE∵AC=2DE,∴设DE=x,则AC=2x, 则AC2﹣AD2=ADDE,(2x)2﹣AD2=ADx, 整理得:AD2+ADx﹣20x2=0,解得:AD=4x或﹣4.5x(负数舍去), 则DC==2x,故tan∠ABD=tan∠ACD===2. 12、解:(1)AP=BQ.理由:∵四边形ABCD是正方形,∴AB=BC,∠ABC=∠C=90°, ∴∠ABQ+∠CBQ=90°.∵BQ⊥AP,∴∠PAB+∠QBA=90°,∴∠PAB=∠CBQ. 在△PBA和△QCB中, ,∴△PBA≌△QCB,∴AP=BQ; (2)过点Q作QH⊥AB于H,如图.∵四边形ABCD是正方形, ∴QH=BC=AB=3.∵BP=2PC,∴BP=2,PC=1, ∴BQ=AP===, ∴BH===2.∵四边形ABCD是正方形,∴DC∥AB,∴∠CQB=∠QBA. 由折叠可得∠C′QB=∠CQB,∴∠QBA=∠C′QB,∴MQ=MB.设QM=x,则有MB=x,MH=x﹣2. 在Rt△MHQ中,根据勾股定理可得x2=(x﹣2)2+32,解得x=.∴QM的长为; (3)过点Q作QH⊥AB于H,如图.∵四边形ABCD是正方形,BP=m,PC=n, ∴QH=BC=AB=m+n.∴BQ2=AP2=AB2+PB2,∴BH2=BQ2﹣QH2=AB2+PB2﹣AB2=PB2,∴BH=PB=m. 设QM=x,则有MB=QM=x,MH=x﹣m.在Rt△MHQ中,根据勾股定理可得x2=(x﹣m)2+(m+n)2, 解得x=m+n+,∴AM=MB﹣AB=m+n+﹣m﹣n=.∴AM的长为. 13、证明:(1)如图1,连接FO,∵F为BC的中点,AO=CO, ∴OF∥AB,∵AC是⊙O的直径,∴CE⊥AE,∵OF∥AB, ∴OF⊥CE,∴OF所在直线垂直平分CE,∴FC=FE,OE=OC, ∴∠FEC=∠FCE,∠0EC=∠0CE,∵∠ACB=90°, 即:∠0CE+∠FCE=90°,∴∠0EC+∠FEC=90°,即:∠FEO=90°, ∴FE为⊙O的切线; (2)如图2,∵⊙O的半径为3,∴AO=CO=EO=3,∵∠EAC=60°,OA=OE, ∴∠EOA=60°,∴∠COD=∠EOA=60°,∵在Rt△OCD中,∠COD=60°,OC=3, ∴CD=,∵在Rt△ACD中,∠ACD=90°,CD=,AC=6,∴AD=. 14、解:(1)连接AC,∵点CD是半圆O的三等分点,∴==,∴∠DAC=∠CAB, ∵OA=OC,∴∠CAB=∠OCA,∴∠DAC=∠OCA,∴AE∥OC ∴∠OCE=∠E,∵CE⊥AD,∴∠OCE=90°,∴OC⊥CE,∴CE是⊙O的切线; (2)四边形AOCD为菱形.理由是:∵=,∴∠DCA=∠CAB, ∴CD∥OA,又∵AE∥OC,∴四边形AOCD是平行四边形,∵OA=OC, ∴平行四边形AOCD是菱形. 15、解:(1)∵点A(,0)与点B(0,﹣),∴OA=,OB=, ∴AB==2,∵∠AOB=90°,∴AB是直径,∴⊙M的半径为:; (2)∵∠COD=∠CBO,∠COD=∠CBA,∴∠CBO=∠CBA,即BD平分∠ABO; (3)如图,过点A作AE⊥AB,垂足为A,交BD的延长线于点E,过点E作EF⊥OA于点F,即AE是切线, ∵在Rt△AOB中,tan∠OAB===,∴∠OAB=30°, ∴∠ABO=90°﹣∠OAB=60°,∴∠ABC=∠OBC=∠ABO=30°,∴OC=OB•tan30°=×=, ∴AC=OA﹣OC=,∴∠ACE=∠ABC+∠OAB=60°,∴∠EAC=60°, ∴△ACE是等边三角形,∴AE=AC=,∴AF=AE=,EF=AE=,∴OF=OA﹣AF=, ∴点E的坐标为:(,). 16、 1)证明:∵AD是直径, ∴∠ABD=∠ACD=90°, 在Rt△ABD和Rt△ACD中, ,∴Rt△ABD≌Rt△ACD,∴∠BAD=∠CAD,∵AB=AC,∴BE=CE; (2)四边形BFCD是菱形. 证明:∵AD是直径,AB=AC,∴AD⊥BC,BE=CE,∵CF∥BD,∴∠FCE=∠DBE, 在△BED和△CEF中 ,∴△BED≌△CEF,∴CF=BD,∴四边形BFCD是平行四边形, ∵∠BAD=∠CAD,∴BD=CD,∴四边形BFCD是菱形; (3)解:∵AD是直径,AD⊥BC,BE=CE,∴CE2=DE•AE,设DE=x,∵BC=8,AD=10, ∴42=x(10﹣x),解得:x=2或x=8(舍去)在Rt△CED中,CD===2. 17、(1)证明:如图,连接OD.∵AC⊥AB,∴∠BAC=90°,即∠OAE=90°. 在△AOE与△DOE中, ,∴△AOE≌△DOE(SSS), ∴∠OAE=∠ODE=90°,即OD⊥ED.又∵OD是⊙O的半径, ∴ED是⊙O的切线; (2)解:如图,在△OAE中,∠OAE=90°,OA=3,AE=4, ∴由勾股定理易求OE=5.∵AB是直径,∴∠ADB=90°,即AD⊥BC. 又∵由(1)知,△AOE≌△DOE,∴∠AEO=∠DEO, 又∵AE=DE,∴OE⊥AD,∴OE∥BC,∴==. BC=2OE=10,即BC的长度是10. 18、(1)证明:∵四边形ABCD是矩形,∴∠A=∠B=90°.∵EF⊥DE, ∴∠DEF=90°.∴∠AED=90°﹣∠BEF=∠EFB. ∵∠A=∠B,∠AED=∠EFB,∴△ADE∽△BEF. (2)解:∵DF与⊙O相切于点G,∴OG⊥DG.∴∠DGO=90°. ∵DH=OH=OG,∴sin∠ODG==.∴∠ODG=30°.∴∠GOE=120°. ∴S扇形OEG==3π. 在Rt△DGO中,cos∠ODG===.∴DG=3.在Rt△DEF中, tan∠EDF===.∴EF=3.∴S△DEF=DE•EF=×9×3=, S△DGO=DG•GO=×3×3=.∴S阴影=S△DEF﹣S△DGO﹣S扇形OEG=﹣﹣3π=.9﹣3π ≈9×1.73﹣3×3.14=6.15≈6.2 ∴图中阴影部分的面积约为6.2. 19、(1)证明:连结OC,如图,∵AC⊥OB,∴AM=CM, ∴OB为线段AC的垂直平分线,∴BA=BC, 在△OAB和△OCB中 ,∴△OAB≌△OCB,∴∠OAB=∠OCB, ∵OA⊥AB,∴∠OAB=90°,∴∠OCB=90°,∴OC⊥BC,∴BC是⊙O的切线; (2)解:在Rt△OAB中,OA=1,AB=,∴OB==2,∴∠ABO=30°,∠AOB=60°, ∵PB⊥OB,∴∠PBO=90°,在Rt△PBO中,OB=2,∠BPO=30°,∴PB=OB=2, 在Rt△PBD中,BD=OB﹣OD=2﹣1=1,PB=2,∴PD==, ∴sin∠BPD===.查看更多