- 2021-05-10 发布 |
- 37.5 KB |
- 8页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
◇中考数学中等难度题训练2√
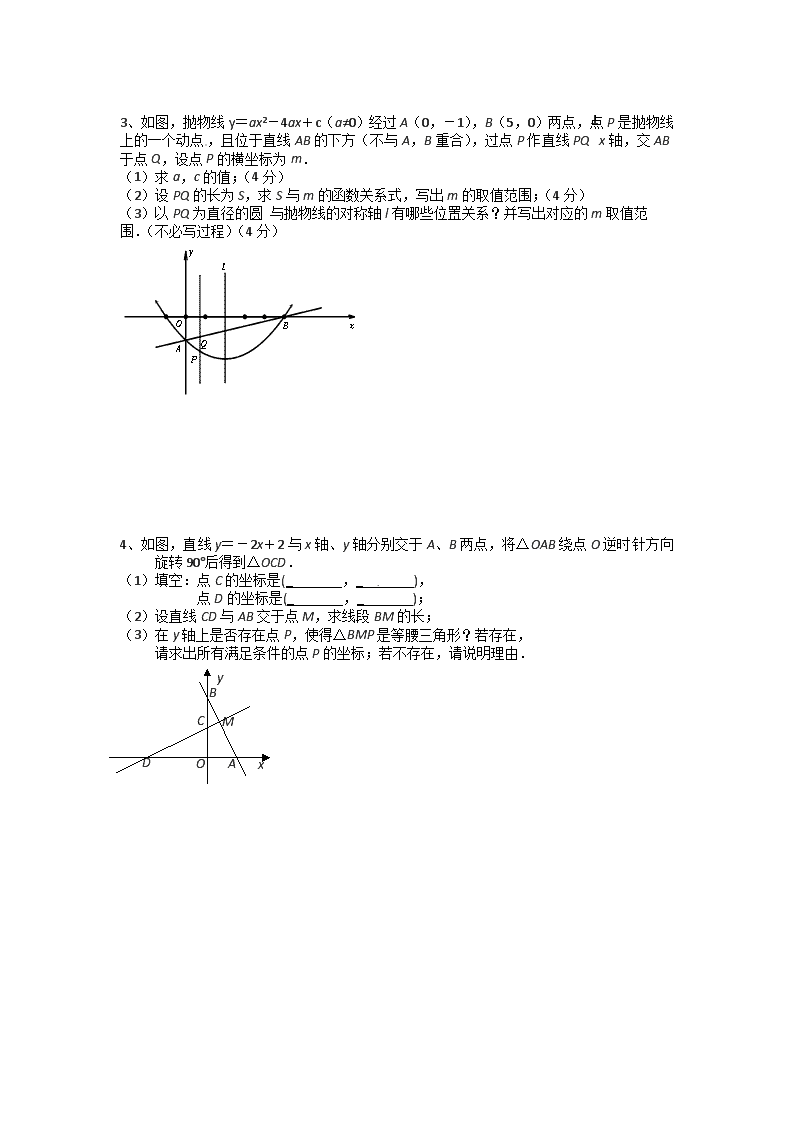
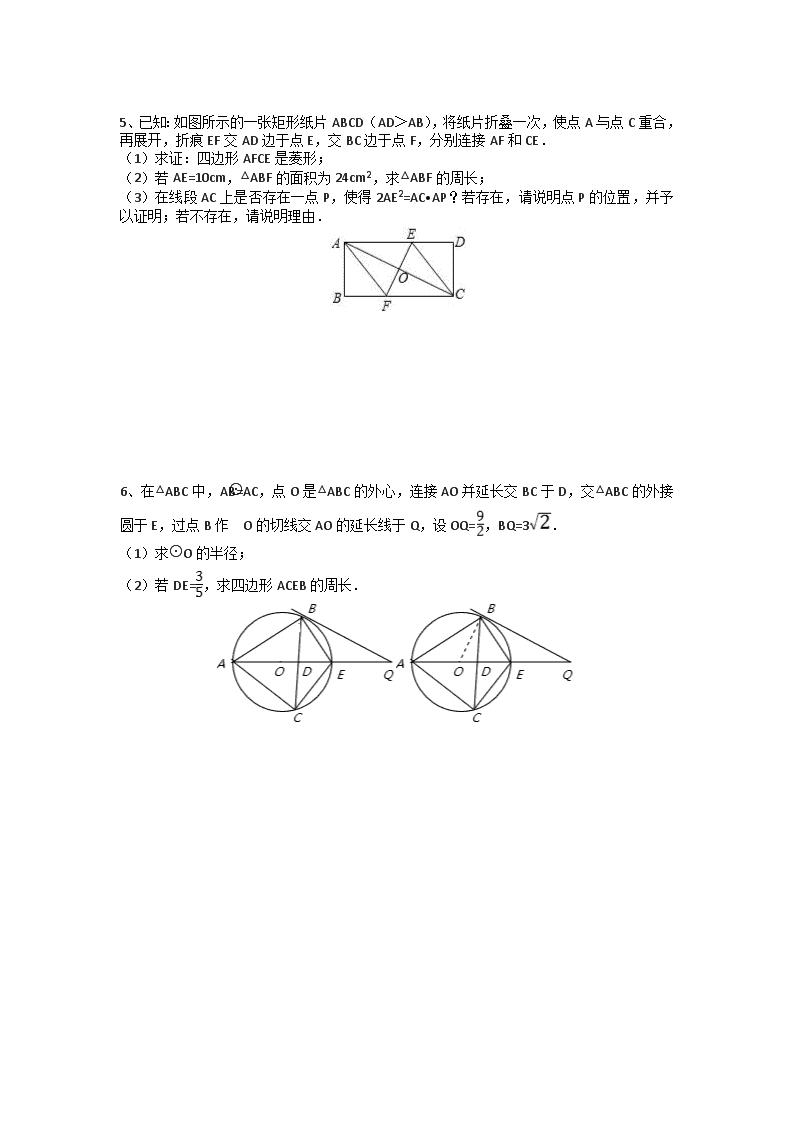
中等难度题训练2 1、(1)操作发现:如图1,在矩形ABCD中,E是BC的中点,将△ABE沿AE折叠后得到△AFE,点F在矩形ABCD内部,延长AF交CD于点G.猜想线段GF与GC有何数量关系?并证明你的结论. (2)类比探究: 如图2,将(1)中的矩形ABCD改为平行四边形,其它条件不变,(1)中的结论是否仍然成立?请说明理由. A B E F G C D C E D F B A G 2、已知抛物线的对称轴为直线,且与x轴交于A、B两点.与y轴交于点C.其中AI(1,0),C(0,). (1)(3分)求抛物线的解析式; (2)若点P在抛物线上运动(点P异于点A). ①(4分)如图l.当△PBC面积与△ABC面积相等时.求点P的坐标; ②(5分)如图2.当∠PCB=∠BCA时,求直线CP的解析式。 3、如图,抛物线y=ax2-4ax+c(a≠0)经过A(0,-1),B(5,0)两点,点P是抛物线上的一个动点,且位于直线AB的下方(不与A,B重合),过点P作直线PQ⊥x轴,交AB于点Q,设点P的横坐标为m. (1)求a,c的值;(4分) (2)设PQ的长为S,求S与m的函数关系式,写出m的取值范围;(4分) (3)以PQ为直径的圆 与抛物线的对称轴l有哪些位置关系?并写出对应的m取值范围.(不必写过程)(4分) 4、如图,直线y=-2x+2与x轴、y轴分别交于A、B两点,将△OAB绕点O逆时针方向旋转90°后得到△OCD. (1)填空:点C的坐标是(_ ,_ ), 点D的坐标是(_ ,_ ); (2)设直线CD与AB交于点M,求线段BM的长; (3)在y轴上是否存在点P,使得△BMP是等腰三角形?若存在, 请求出所有满足条件的点P的坐标;若不存在,请说明理由. A O D C M B y x 5、已知:如图所示的一张矩形纸片ABCD(AD>AB),将纸片折叠一次,使点A与点C重合,再展开,折痕EF交AD边于点E,交BC边于点F,分别连接AF和CE. (1)求证:四边形AFCE是菱形; (2)若AE=10cm,△ABF的面积为24cm2,求△ABF的周长; (3)在线段AC上是否存在一点P,使得2AE2=AC•AP?若存在,请说明点P的位置,并予以证明;若不存在,请说明理由. 6、在△ABC中,AB=AC,点O是△ABC的外心,连接AO并延长交BC于D,交△ABC的外接圆于E,过点B作⊙O的切线交AO的延长线于Q,设OQ=,BQ=3. (1)求⊙O的半径; (2)若DE=,求四边形ACEB的周长. 中等难度题训练2 1、(1)操作发现:如图1,在矩形ABCD中,E是BC的中点,将△ABE沿AE折叠后得到△AFE,点F在矩形ABCD内部,延长AF交CD于点G.猜想线段GF与GC有何数量关系?并证明你的结论. (2)类比探究: 如图2,将(1)中的矩形ABCD改为平行四边形,其它条件不变,(1)中的结论是否仍然成立?请说明理由. A B E F G C D C E D F B A G 【答案】(1)连接FC, A B E F G C D 1 2 3 4 由折叠知:BE=EF ∠AFE=∠B=90° ∴∠EFG=∠C=90° ∵E是BC的中点,∴BE=CE ∴CE=EF ∴∠1=∠2 ∵∠EFG=∠C ∴∠3=∠4 ∴FG=CG C E D F B A G 1 2 3 4 (2)连接CF, 由折叠知:BE=EF ∠AFE=∠B ∵E是BC的中点,∴BE=CE ∴CE=EF ∴∠1=∠2 又∵∠AFE+∠EFG=180° ∠B+∠ECG=180° ∴∠EFG=∠ECG ∴∠3=∠4 ∴FG=CG 2、已知抛物线的对称轴为直线,且与x轴交于A、B两点.与y轴交于点C.其中AI(1,0),C(0,). (1)(3分)求抛物线的解析式; (2)若点P在抛物线上运动(点P异于点A). ①(4分)如图l.当△PBC面积与△ABC面积相等时.求点P的坐标; ②(5分)如图2.当∠PCB=∠BCA时,求直线CP的解析式。 解:(1)由题意,得,解得 ∴抛物线的解析式为。 (2)①令,解得 ∴B(3, 0) 当点P在x轴上方时,如图1, 过点A作直线BC的平行线交抛物线于点P, 易求直线BC的解析式为, ∴设直线AP的解析式为, ∵直线AP过点A(1,0),代入求得。 ∴直线AP的解析式为 解方程组,得 ∴点 当点P在x轴下方时,如图1 设直线交y轴于点, 把直线BC向下平移2个单位,交抛物线于点, 得直线的解析式为, 解方程组,得 ∴ 综上所述,点P的坐标为:, ②∵ ∴OB=OC,∴∠OCB=∠OBC=45°设直线CP的解析式为 如图2,延长CP交x轴于点Q,设∠OCA=α,则∠ACB=45°α ∵∠PCB=∠BCA ∴∠PCB=45°α ∴∠OQC=∠OBC-∠PCB=45°-(45°α)=α ∴∠OCA=∠OQC 又∵∠AOC=∠COQ=90° ∴Rt△AOC∽Rt△COQ ∴,∴,∴OQ=9,∴ ∵直线CP过点,∴ ∴ ∴直线CP的解析式为。 3、如图,抛物线y=ax2-4ax+c(a≠0)经过A(0,-1),B(5,0)两点,点P是抛物线上的一个动点,且位于直线AB的下方(不与A,B重合),过点P作直线PQ⊥x轴,交AB于点Q,设点P的横坐标为m. (1)求a,c的值;(4分) (2)设PQ的长为S,求S与m的函数关系式,写出m的取值范围;(4分) (3)以PQ为直径的圆 与抛物线的对称轴l有哪些位置关系?并写出对应的m取值范围.(不必写过程)(4分) 解:∵抛物线y=ax2-4ax+c过A(0,-1),B(5,0) ∴ 解得: (2)∵直线AB经过A(0,-1),B(5,0)∴直线AB的解析式为y=x -1 由(1)知抛物线的解析式为:y=x2-x-1 ∵点P的横坐标为m,点P在抛物线上,点Q在直线AB上,PQ⊥x轴 ∴P(m,m 2-m-1),Q(m,m -1)∴S=PQ=(m -1)-(m 2-m-1) 即S=-m 2+m (0<m<5) (3)抛物线的对称轴l为:x=2 以PQ为直径的圆与抛物线的对称轴l的位置关系有: 相离、相切、相交三种关系 相离时:0<m<或 <m<5; 相切时:m= m=; 相交时:<m< 4、如图,直线y=-2x+2与x轴、y轴分别交于A、B两点,将△OAB绕点O逆时针方向旋转90°后得到△OCD. (1)填空:点C的坐标是(_ ,_ ), 点D的坐标是(_ ,_ ); (2)设直线CD与AB交于点M,求线段BM的长; A O D C M B y x (3)在y轴上是否存在点P,使得△BMP是等腰三角形?若存在, 请求出所有满足条件的点P的坐标;若不存在,请说明理由. 解:(1)点C的坐标是(0,1),点D的坐标是(-2,0) (2)方法一:由(1)可知CD= =,BC=1 又∠1=∠5,∠4=∠3 ∴△BMC∽△DOC ∴= 即=∴B M= 方法二:设直线CD的解析式为y=kx+b A O D C M B y x P1 · · P2 1 5 由(1)得 解得 ∴直线CD的解析式为y= x+1 又∠1=∠5,∠BCM=∠DCO ∴△BMC∽△DOC ∴= 即= ∴BM= ∵ ∴ ∴M的坐标为(,) A O D C M B y x P3 · E 过点M作ME⊥y轴于点E,则ME=,BE= ∴BM= = (3)存在 分两种情况讨论: ① 以BM为腰时 ∵BM=,又点P在y轴上,且BP=BM 此时满足条件的点P有两个,它们是P1 (0,2+)、P2 (0,2-) A O D C M B y x P4 · F 过点M作ME⊥y轴于点E,∵∠BMC=90°, 则△BME∽△BCM ∴= ∴BE== 又∵BM=BP ∴PE=BE= ∴BP= ∴OP=2-= 此时满足条件的点P有一个,它是P3 (0,) ② 以BM为底时,作BM的垂直平分线,分别交y轴、BM于点P、F, 由(2)得∠BMC=90°,∴PF∥CM ∵F是BM的中点,∴BP=BC=∴OP= 此时满足条件的点P有一个,它是P4 (0,) 综上,符合条件的点P有四个:P1 (0,2+)、P2 (0,2-)、P3 (0,)、P4 (0,) 5、已知:如图所示的一张矩形纸片ABCD(AD>AB),将纸片折叠一次,使点A与点C重合,再展开,折痕EF交AD边于点E,交BC边于点F,分别连接AF和CE. (1)求证:四边形AFCE是菱形; (2)若AE=10cm,△ABF的面积为24cm2,求△ABF的周长; (3)在线段AC上是否存在一点P,使得2AE2=AC•AP?若存在,请说明点P的位置,并予以证明;若不存在,请说明理由. 解答:(1)证明:由题意可知OA=OC,EF⊥AO, ∵AD∥BC, ∴∠AEO=∠CFO,∠EAO=∠FCO,∴△AOE≌△COF,∴AE=CF,又AE∥CF,∴四边形AECF是平行四边形, ∵AC⊥EF,∴四边形AECF是菱形; (2)∵四边形AECF是菱形,∴AF=AE=10cm, 设AB=a,BF=b, ∵△ABF的面积为24cm2,∴a2+b2=100,ab=48,∴(a+b)2=196, ∴a+b=14或a+b=﹣14(不合题意,舍去),∴△ABF的周长为14+10=24cm; (3)存在,过点E作AD的垂线,交AC于点P,点P就是符合条件的点; 证明:∵∠AEP=∠AOE=90°,∠EAO=∠EAP, ∴△AOE∽△AEP,∴=,∴AE2=AO•AP, ∵四边形AECF是菱形, ∴AO=AC, ∴AE2=AC•AP, ∴2AE2=AC•AP. 6、在△ABC中,AB=AC,点O是△ABC的外心,连接AO并延长交BC于D,交△ABC的外接圆于E,过点B作⊙O的切线交AO的延长线于Q,设OQ=,BQ=3. (1)求⊙O的半径; (2)若DE=,求四边形ACEB的周长. 解:(1)连接OB. ∵BQ与⊙O相切, ∴∠OBQ=90° ∴OB===.故半径是:; (2)∵AB=AC,O是△ABC的内心. ∴=,=∴AB=AC,BE=CE∴BC⊥AE ∵OE=OB=,∴OD=OE﹣DE=﹣= ∴在直角△ODB中,BD2=OB2﹣OD2=()2﹣()2== 在直角△BDE中,BE=== ∴CE=BE= ∵AE是直径.∴∠ABE=90° ∴在直角△ABE中,AE=2OB=2×=3,AB===.∴AC=AB=. ∴四边形ACEB的周长是:AB+AC+CE+BE=+++=.查看更多