丽水市中考模拟卷

丽水市中考模拟卷

丽水市数学中考模拟卷 一、选择题(本题有10小题,每小题3分,共30分)‎ ‎1. 在数0，，，-1中，其中最小的数是【 】‎ A. 0 B. C. D. -1‎ ‎2. 计算结果正确的是【 】‎ A. B. C. D. ‎ ‎3. 如图是由五个相同的小立方块搭成的几何体，则它的俯视图是【 】‎ ‎4．设a＜b,则下列式子不正确的是【 】‎ ‎ A．a＋3＜b＋3 B．a－2＜b－2 C．-5a＜-5b D．3a＜3b ‎ ‎5. 化简的结果是【 】‎ A. B. C. D. ‎ ‎6. 一个多边形的每个外角均为60°，则这个多边形是【 】‎ A. 四边形 B. 五边形 C. 六边形 D. 七边形 ‎7. 在中秋节来临之前，学校食堂推荐了A，B，C三种不同口味的月饼，对全校师生爱吃哪种口味的月饼作调查，以决定最终的采购。下面的统计量中，最值得关注的是【 】‎ A. 方差 B. 众数 C. 中位数 D. 平均数 第 8 题图 ‎8. 如图，在直角三角形ABC中，∠BAC=90°，作AD⊥BC于点D，则下列用线段比表示的值中，错误的是【 】‎ A. B. C. D. ‎ 第 10 题图 ‎9. 若反比例函数的图象经过点（2，－1），则该反比例函数的图象在【 】‎ A. 第一、二象限 B. 第一、三象限 C. 第二、三象限 D. 第二、四象限 ‎10. 如图，⊙O的直径AB=10，E在⊙O内，且OE=4，则过E点所有弦中，‎ 长度为整数的条数为【 】‎ A．4 B．6 C．8 D．10‎ 二、填空题 (本题有6小题,每小题4分,共24分)‎ ‎11. 分解因式： .‎ ‎12．一个不透明的袋子中装有1个红球，2个白球和3个蓝球，它们除颜色外其余都相同。现随机从袋中摸出一个球，颜色是蓝色的概率是 .‎ ‎13．写出一个解集为x>1的一元一次不等式：___________.‎ ‎14. 如图，已知线段AB与线段BE的夹角为150°，与线段AD的夹角为100°，‎ 若要使BE∥AD，需将线段AD绕点A顺时针旋转__________度。‎ 第16题图 ‎15. 如图，四边形ABCD是菱形，∠DAB=50°，对角线AC，BD相交于点O，DH⊥AB于H，连接OH，则∠DHO=　____　度．‎ 第15题图 第14题图 ‎16. 如图，平行四边形AOBC中，对角线交于点E，双曲线（k＞0）经过A，E两点，若 平行四边形AOBC的面积为18，则k=　________　．‎ 三、解答题（本题有8小题,第17～19题每题6分,第20、21题每题8分,第22、23题每题10 分,第24题12分,共66分,各小题都必须写出解答过程）‎ ‎17． 计算:.‎ 18． 先化简，再求值：，其中.‎ ‎19.如图，已知△ABC，∠C=Rt∠，AC0等，答案不唯一 14. 110°‎ ‎15. 25 16. 6‎ 简答题：‎ ‎17.解 。‎ ‎18.解 化简：‎ ‎ 代入得，原式。‎ ‎19. 解：（1）到点C，B距离相等的点在BC的垂直平分线上，所以利用尺规作出BC的垂直平分线。（需留下作图痕迹）‎ ‎（2） ∵，‎ DE垂直平分BC，‎ ‎∴。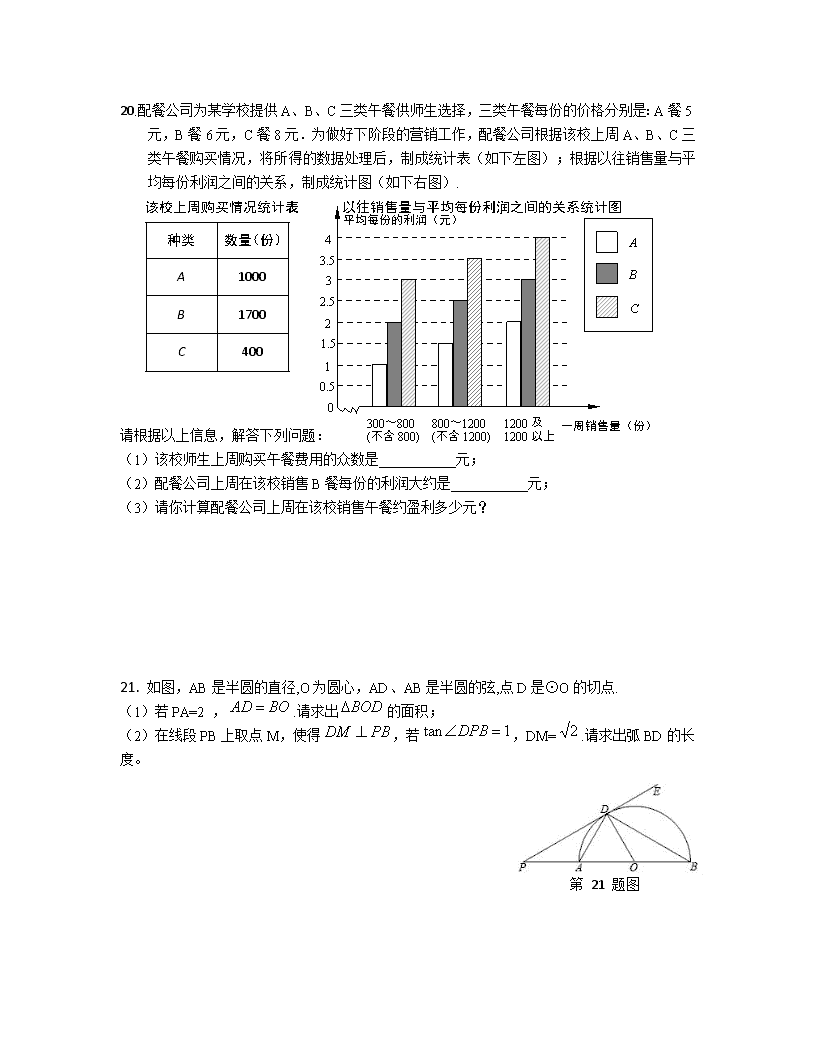‎ ‎∴‎ ‎（2）‎ ‎（1）‎ ‎20.解：‎ （1） ‎∵出现次数最多的是B餐，‎ ‎ ∴该校师生上周购买午餐费用的众数是6元，故答案为6；‎ ‎（2）因为上周在该校销售B餐1700份，由直方图得配餐公司上周在该校销售B餐每份的利润大约是3元；‎ ‎（3）1.5×500+3×800+3×200=750+2400+600=3750（元）．‎ ‎ 答：配餐公司上周在该校销售午餐约盈利3750元．‎ ‎21.（1）解：∵是半圆的直径，点是⊙O的切点.‎ ‎ ∴‎ ‎ ∵ ‎ ‎ ∴ 是正三角形 ‎ ∴ ，‎ ‎ ∴ ‎ ‎ ∵ ，，‎ ‎ ∴ ‎ ‎ ∴的面积是。‎ ‎（2）解：∵点D是是⊙O的切点 .‎ ‎ ∴‎ ‎ ∵ ‎ ‎ ∴ ，‎ ‎ ∴ ‎ ‎ ∵ ‎ ‎ ‎ ‎ ∴弧BD的长度是 ‎22.解：‎ ‎（1）快车的速度120千米/小时；慢车的速度80千米/小时；A、B两站间的距离1200千米。‎ ‎（2）由（120－80）×（15－11）=160得点Q的坐标为（15，720）。‎ 设直线PQ的解析式为，由P（11，880），Q（15，720）得 ‎，解得。∴直线PQ的解析式为。‎ ‎ 设直线QH的解析式为，由Q（15，720），H（21，0）得 ‎ ，解得。∴直线QH的解析式为。‎ ‎ ∴快车从B 返回 A站时，y与x之间的函数关系式为。‎ （3） 出发5小时或7小时或小时，两车相距200千米。‎ ‎23.解：（1）由题意结合图形可得点M坐标为（7，7），点E坐标为（14，0），‎ 设抛物线解析式为：y=ax2+bx，则，解得：，‎ 故抛物线解析式为：y=﹣x2+2x。‎ ‎（2）设A（x，0），则B（14﹣x，0），C（14﹣x，﹣x2+2x），D（x，﹣x2+2x），‎ ‎ 故“脚手架”总长AD+DC+CB=（﹣x2+2x）+（14﹣2x）+（﹣x2+2x）=﹣x2+2x+14=‎ ‎ ﹣（x﹣）2+17.5，‎ ‎ ∵此二次函数的图象开口向下，‎ ‎ ∴当x=3.5米时，L有最大值，最大值为17.5米．‎ ‎24.解：‎ ‎（1）当点P运动时，这两个正方形的面积之和不是定值．‎ 设AP=x，则PB=8﹣x，‎ 根据题意得这两个正方形面积之和=x2+（8﹣x）2=2x2﹣16x+64=2（x﹣4）2+32，‎ 所以当x=4时，这两个正方形面积之和有最小值，最小值为32．‎ ‎（2）存在两个面积始终相等的三角形，它们是△APK与△DFK．‎ 依题意画出图形，如答图2所示．‎ 设AP=a，则PB=BF=8﹣a．‎ ‎∵PE∥BF，‎ ‎∴，即，‎ ‎∴PK=，‎ ‎∴DK=PD﹣PK=a﹣=，‎ ‎∴S△APK=PK•PA=••a=，‎ S△DFK=DK•EF=•（8﹣a）=，‎ ‎∴S△APK=S△DFK．‎ ‎（3）当点P从点A出发，沿A→B→C→D的线路，向点D运动时，不妨设点Q在DA边上，‎ 若点P在点A，点Q在点D，此时PQ的中点O即为DA边的中点；‎ 若点Q在DA边上，且不在点D，则点P在AB上，且不在点A．‎ 此时在Rt△APQ中，O为PQ的中点，所以AO=PQ=4．‎ 所以点O在以A为圆心，半径为4，圆心角为90°的圆弧上．‎ PQ的中点O所经过的路径是三段半径为4，圆心角为90°的圆弧，如答图3所示：‎ 所以PQ的中点O所经过的路径的长为：×2π×4=6π．‎ ‎（4）点O所经过的路径长为3，OM+OB的最小值为．‎ 如答图4﹣1，分别过点G、O、H作AB的垂线，垂足分别为点R、S、T，则四边形GRTH为梯形．‎ ‎∵点O为中点，‎ ‎∴OS=（GR+HT）=（AP+PB）=4，即OS为定值．‎ ‎∴点O的运动路径在与AB距离为4的平行线上．‎ ‎∵MN=6，点P在线段MN上运动，且点O为GH中点，‎ ‎∴点O的运动路径为线段XY，XY=MN=3，XY∥AB且平行线之间距离为4，点X与点A、点Y与点B之间的水平距离均为2.5．‎ 如答图4﹣2，作点M关于直线XY的对称点M′，连接BM′，与XY交于点O．‎ 由轴对称性质可知，此时OM+OB=BM′最小．‎ 在Rt△BMM′中，MM′=2×4=8，BM=7，由勾股定理得：BM′==．‎ ‎∴OM+OB的最小值为．‎