中考数学压轴题专题复习——圆的综合

中考数学压轴题专题复习——圆的综合

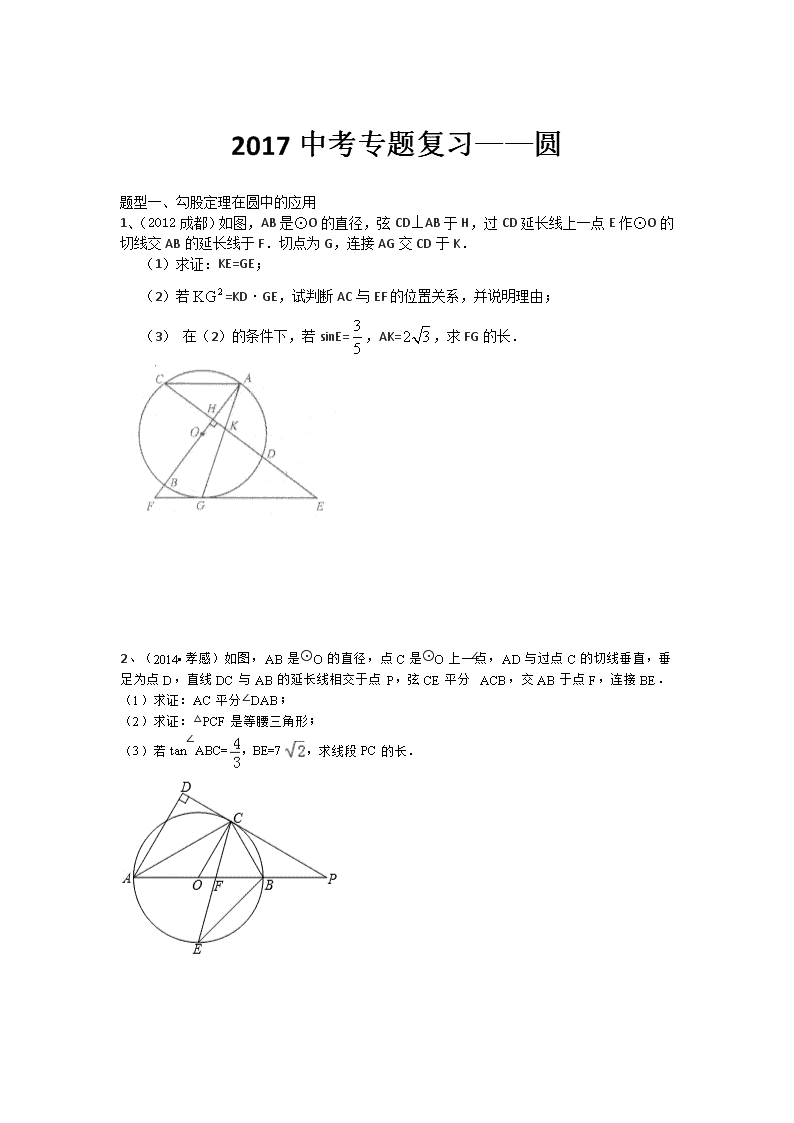
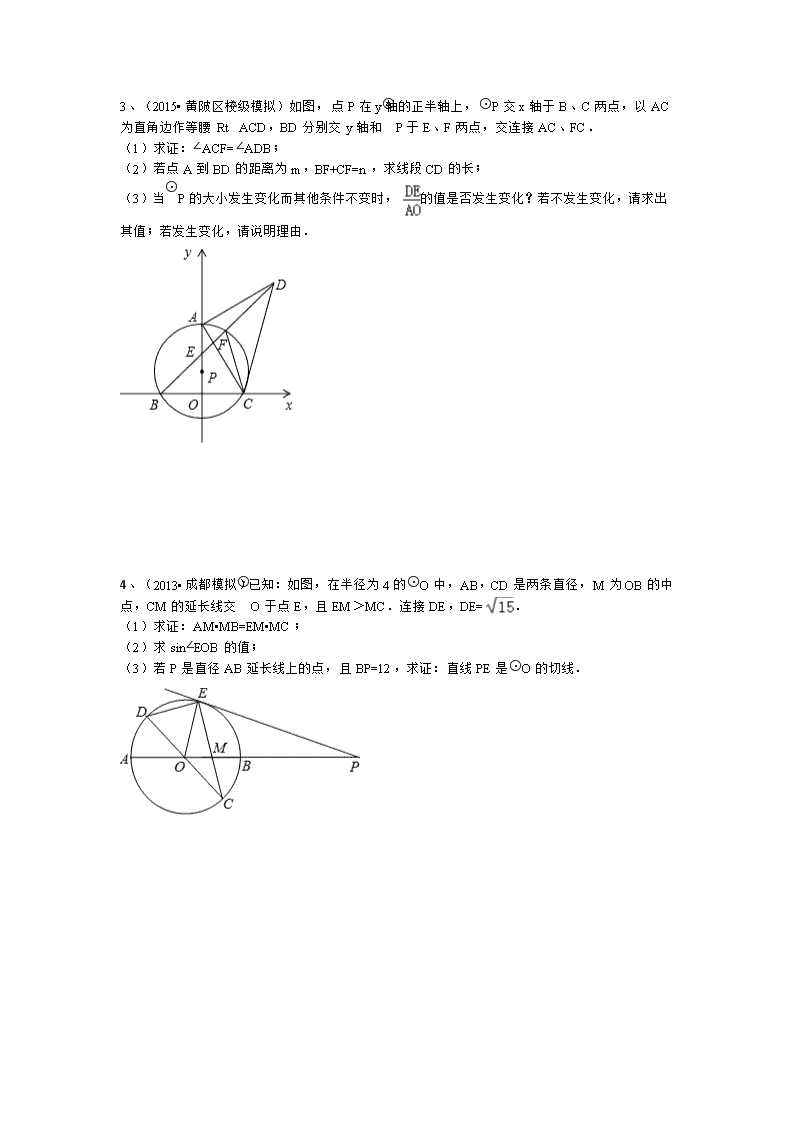
‎2017中考专题复习——圆 题型一、勾股定理在圆中的应用 ‎1、（2012成都）如图，AB是⊙O的直径，弦CD⊥AB于H，过CD延长线上一点E作⊙O的切线交AB的延长线于F．切点为G，连接AG交CD于K．‎ ‎ （1）求证：KE=GE；‎ ‎ （2）若=KD·GE，试判断AC与EF的位置关系，并说明理由；‎ ‎ （3） 在（2）的条件下，若sinE=，AK=，求FG的长．‎ ‎2、（2014•孝感）如图，AB是⊙O的直径，点C是⊙O上一点，AD与过点C的切线垂直，垂足为点D，直线DC与AB的延长线相交于点P，弦CE平分∠ACB，交AB于点F，连接BE．‎ ‎（1）求证：AC平分∠DAB；‎ ‎（2）求证：△PCF是等腰三角形；‎ ‎（3）若tan∠ABC=，BE=7，求线段PC的长．‎ ‎3、（2015•黄陂区校级模拟）如图，点P在y轴的正半轴上，⊙P交x轴于B、C两点，以AC为直角边作等腰Rt△ACD，BD分别交y轴和⊙P于E、F两点，交连接AC、FC．‎ ‎（1）求证：∠ACF=∠ADB；‎ ‎（2）若点A到BD的距离为m，BF+CF=n，求线段CD的长；‎ ‎（3）当⊙P的大小发生变化而其他条件不变时，的值是否发生变化？若不发生变化，请求出其值；若发生变化，请说明理由．‎ ‎4、（2013•成都模拟）已知：如图，在半径为4的⊙O中，AB，CD是两条直径，M为OB的中点，CM的延长线交⊙O于点E，且EM＞MC．连接DE，DE=．‎ ‎（1）求证：AM•MB=EM•MC；‎ ‎（2）求sin∠EOB的值；‎ ‎（3）若P是直径AB延长线上的点，且BP=12，求证：直线PE是⊙O的切线．‎ ‎5、（2012•杭州）如图，AE切⊙O于点E，AT交⊙O于点M，N，线段OE交AT于点C，OB⊥AT于点B，已知∠EAT=30°，AE=3，MN=2．‎ ‎（1）求∠COB的度数；‎ ‎（2）求⊙O的半径R；‎ ‎（3）点F在⊙O上（是劣弧），且EF=5，把△OBC经过平移、旋转和相似变换后，使它的两个顶点分别与点E，F重合．在EF的同一侧，这样的三角形共有多少个？你能在其中找出另一个顶点在⊙O上的三角形吗？请在图中画出这个三角形，并求出这个三角形与△OBC的周长之比．‎ ‎6、（2011•潍坊）如图，AB是半径O的直径，AB=2．射线AM、BN为半圆O的切线．在AM上取一点D，连接BD交半圆于点C，连接AC．过O点作BC的垂线OE，垂足为点E，与BN相交于点F．过D点作半圆O的切线DP，切点为P，与BN相交于点Q．‎ ‎（1）求证：△ABC∽△OFB；‎ ‎（2）当△ABD与△BFO的面枳相等时，求BQ的长；‎ ‎（3）求证：当D在AM上移动时（A点除外），点Q始终是线段BF的中点．‎ 专题二、三角函数在圆中的应用 ‎1、（2014成都）如图，在⊙的内接△ABC中，∠ACB=90°，AC=2BC，过C作AB的垂线交⊙O于另一点D，垂足为E.设P是上异于A,C的一个动点，射线AP交于点F，连接PC与PD，PD交AB于点G.‎ ‎（1）求证：△PAC∽△PDF；‎ ‎（2）若AB=5，=，求PD的长；‎ ‎（3）在点P运动过程中，设，，求与之间的函数关系式.（不要求写出的取值范围）‎ ‎，‎ ‎2、（2012•襄阳）如图，PB为⊙O的切线，B为切点，直线PO交⊙于点E、F，过点B作PO的垂线BA，垂足为点D，交⊙O于点A，延长AO与⊙O交于点C，连接BC，AF．‎ ‎（1）求证：直线PA为⊙O的切线；‎ ‎（2）试探究线段EF、OD、OP之间的等量关系，并加以证明；‎ ‎（3）若BC=6，tan∠F=，求cos∠ACB的值和线段PE的长．‎ ‎　‎ ‎3、（2014•武侯区校级自主招生）如图，⊙O与直线PC相切于点C，直径AB∥PC，PA交⊙O于D，BP交⊙O于E，DE交PC于F．‎ ‎（1）求证：PF2=EF•FD；‎ ‎（2）当tan∠APB=，tan∠ABE=，AP=时，求PF的长；‎ ‎（3）在（2）条件下，连接BD，判断△ADB是什么三角形？并证明你的结论．‎ ‎4、（2014•盘锦）如图，△ABC中，∠C=90°，点G是线段AC上的一动点（点G不与A、C重合），以AG为直径的⊙O交AB于点D，直线EF垂直平分BD，垂足为F，EF交BC于点E，连结DE．‎ ‎（1）求证：DE是⊙O的切线；‎ ‎（2）若cosA=，AB=8，AG=2，求BE的长；‎ ‎（3）若cosA=，AB=8，直接写出线段BE的取值范围．‎ 专题三、相似三角形与圆的综合应用 ‎1、（2010）已知：如图，内接于，为直径，弦于，是的中点，连结并延长交的延长线于点，连结，分别交、于点、．‎ ‎ （1）求证：是的外心；‎ ‎ （2）若,求的长；‎ ‎ （3）求证：．‎ ‎2、（2014•镇江）如图，⊙O的直径AC与弦BD相交于点F，点E是DB延长线上的一点，∠EAB=∠ADB．‎ ‎（1）求证：EA是⊙O的切线；‎ ‎（2）已知点B是EF的中点，求证：以A、B、C为顶点的三角形与△AEF相似；‎ ‎（3）已知AF=4，CF=2．在（2）条件下，求AE的长．‎ ‎3、（2013•桂林）如图，在△ABC中，∠C=90°，∠BAC的平分线AD交BC于D，过点D作DE⊥AD交AB于E，以AE为直径作⊙O．‎ ‎（1）求证：点D在⊙O上；‎ ‎（2）求证：BC是⊙O的切线；‎ ‎（3）若AC=6，BC=8，求△BDE的面积．‎ ‎4、（2012•泰州）如图，已知直线l与⊙O相离，OA⊥l于点A，OA=5．OA与⊙O相交于点P，AB与⊙O相切于点B，BP的延长线交直线l于点C．‎ ‎（1）试判断线段AB与AC的数量关系，并说明理由；‎ ‎（2）若PC=2，求⊙O的半径和线段PB的长；‎ ‎（3）若在⊙O上存在点Q，使△QAC是以AC为底边的等腰三角形，求⊙O的半径r的取值范围．‎ ‎5、（2012•德阳）如图，已知点C是以AB为直径的⊙O上一点，CH⊥AB于点H，过点B作⊙O的切线交直线AC于点D，点E为CH的中点，连接AE并延长交BD于点F，直线CF交AB的延长线于G．‎ ‎（1）求证：AE•FD=AF•EC；‎ ‎（2）求证：FC=FB；‎ ‎（3）若FB=FE=2，求⊙O的半径r的长．‎ ‎6、如图，在Rt△ABC中，∠B=90°，它的内切圆分别与三角形的三边切于点D,E,F，连接AD与内切圆相交于点P，连接PC,PE,PF,FD,ED，且PC⊥PF。‎ （1） 求证：△PFD∽△PDC；‎ （2） ‎7、（2012•十堰）如图1，⊙O是△ABC的外接圆，AB是直径，OD∥AC，且∠CBD=∠BAC，OD交⊙O于点E．‎ ‎（1）求证：BD是⊙O的切线；‎ ‎（2）若点E为线段OD的中点，证明：以O、A、C、E为顶点的四边形是菱形；‎ ‎（3）作CF⊥AB于点F，连接AD交CF于点G（如图2），求的值．‎ ‎　‎ ‎8、（2004•武汉）已知：如图，直线y=kx+3（k＞0）交x轴于B点，交y轴于A点，以A为圆心，AB为半径作⊙A交x轴于另一点D，交y轴于E、F两点，交直线AB于C点，连接BE、CE，∠CBD的平分线交CE于I点．‎ ‎（1）求证：BE=IE；‎ ‎（2）若AI⊥CE，设Q为弧BF上一点，连接DQ交y轴于T，连接BQ并延长交y轴于G点，求AT•AG的值；‎ ‎（3）设P为线段AB上的一个动点（异于A、B），连接PD交y轴于M点，过P、M、B三点作⊙O1交y轴于另一点N．设⊙O1的半径为R，当时，给出下列两个结论：①MN的长度不变；②的值不变，其中有且只有一个结论是正确的，请你判断哪一个结论正确，证明正确的结论并求出其值．‎ 专题四、圆中的面积问题 ‎1、（2013）如图，⊙的半径，四边形内接圆⊙，于点，为延长线上的一点，且.‎ ‎（1）试判断与⊙的位置关系，并说明理由：‎ ‎（2）若，，求的长；‎ ‎（3）在（2）的条件下，求四边形的面积.‎ ‎2、（2013•钦州）如图，在Rt△ABC中，∠A=90°，O是BC边上一点，以O为圆心的半圆与AB边相切于点D，与AC、BC边分别交于点E、F、G，连接OD，已知BD=2，AE=3，tan∠BOD=．‎ ‎（1）求⊙O的半径OD；‎ ‎（2）求证：AE是⊙O的切线；‎ ‎（3）求图中两部分阴影面积的和．‎ ‎3、如图，圆O的直径为5，在圆O上位于直径AB的异侧有定点C和动点P，已知BC : CA＝4 : 3，点P在半圆弧AB上运动（不与A、B两点重合），过C作CP的垂线CD交PB的延长线于D点．‎ ‎（1）求证：AC·CD＝PC·BC；‎ ‎（2）当点P运动到AB弧中点时，求CD的长；‎ ‎（3）当点P运动到什么位置时，△PCD的面积最大？并求这个最大面积S．‎ ‎4、（四川省成都市2009）如图，Rt△ABC内接于⊙O，AC＝BC，∠BAC的平分线AD与⊙O交于点D，与BC交于点E，延长BD，与AC的延长线交于点F，连结CD，G是CD的中点，连结OG．‎ ‎（1）判断OG与CD的位置关系，写出你的结论并证明；‎ ‎（2）求证：AE＝BF；‎ ‎（3）若OG·DE＝3(2－)，求⊙O的面积．‎ ‎5、如图，⊙O的半径为1，点P是⊙O上一点，弦AB垂直平分线段OP，点D是弧 上的任一点（与端点A、B不重合），DE⊥AB于点E，以D为圆心、DE长为半径作⊙D，分别过点A、B作⊙D的切线，两条切线相交于点C．‎ ‎（1）求弦AB的长； ‎ ‎（2）判断∠ACB是否为定值，若是，求出∠ACB的大小；否则，请说明理由；‎ ‎（3）记△ABC的面积为S，若＝，求△ABC的周长．‎ ‎6、如图，等圆⊙O1和⊙O2相交于A、B两点，⊙O1经过⊙O2的圆心，顺次连接A、O1、B、O2．‎ ‎（1）求证：四边形AO1BO2是菱形；‎ ‎（2）过直径AC的端点C作⊙O1的切线CE交AB的延长线于E，连接CO2交AE于D，求证：CE＝2O2D；‎ ‎（3）在(2)的条件下，若△AO2D的面积为1，求△BO2D的面积．‎ 专题五、中点在圆中的应用 ‎1、（2011）已知：如图，以矩形ABCD的对角线AC的中点O为圆心，OA长为半径作⊙O，⊙O经过B、D两点，过点B作BK⊥ A C，垂足为K。过D作DH∥KB，DH分别与AC、AB、⊙O及CB的延长线相交于点E、F、G、H．‎ ‎(1)求证：AE=CK；‎ ‎ (2)如果AB=，AD= (为大于零的常数)，求BK的长：‎ ‎(3)若F是EG的中点，且DE=6，求⊙O的半径和GH的长．‎ ‎2、（2014•长沙）如图，以△ABC的一边AB为直径作⊙O，⊙O与BC边的交点恰好为BC的中点D，过点D作⊙O的切线交AC于点E．‎ ‎（1）求证：DE⊥AC；‎ ‎（2）若AB=3DE，求tan∠ACB的值．‎ ‎3、（2014•广安）如图，AB为⊙O的直径，以AB为直角边作Rt△ABC，∠CAB=90°，斜边BC与⊙O交于点D，过点D作⊙O的切线DE交AC于点E，DG⊥AB于点F，交⊙O于点G．‎ ‎（1）求证：E是AC的中点；‎ ‎（2）若AE=3，cos∠ACB=，求弦DG的长．‎ ‎4、（2010•苏州）如图，在等腰梯形ABCD中，AD∥BC．O是CD边的中点，以O为圆心，OC长为半径作圆，交BC边于点E．过E作EH⊥AB，垂足为H．已知⊙O与AB边相切，切点为F．‎ ‎（1）求证：OE∥AB；‎ ‎（2）求证：EH=AB；‎ ‎（3）若，求的值．‎ ‎5、011•广州）如图1，⊙O中AB是直径，C是⊙O上一点，∠ABC=45°，等腰直角三角形DCE中∠DCE是直角，点D在线段AC上．‎ ‎（1）证明：B、C、E三点共线；‎ ‎（2）若M是线段BE的中点，N是线段AD的中点，证明：MN=OM；‎ ‎（3）将△DCE绕点C逆时针旋转α（0°＜α＜90°）后，记为△D1CE1（图2），若M1是线段BE1的中点，N1是线段AD1的中点，M1N1=OM1是否成立？若是，请证明；若不是，说明理由．‎ ‎6、（2011•金华）如图，在平面直角坐标系中，点A（10，0），以OA为直径在第一象限内作半圆C，点B是该半圆周上一动点，连接OB、AB，并延长AB至点D，使DB=AB，过点D作x轴垂线，分别交x轴、直线OB于点E、F，点E为垂足，连接CF．‎ ‎（1）当∠AOB=30°时，求弧AB的长度；‎ ‎（2）当DE=8时，求线段EF的长；‎ ‎（3）在点B运动过程中，是否存在以点E、C、F为顶点的三角形与△AOB相似？若存在，请求出此时点E的坐标；若不存在，请说明理由．‎ ‎/2015中考圆答案 ‎1、（略）‎ ‎2、（2014•孝感）如图，AB是⊙O的直径，点C是⊙O上一点，AD与过点C的切线垂直，垂足为点D，直线DC与AB的延长线相交于点P，弦CE平分∠ACB，交AB于点F，连接BE．‎ ‎（1）求证：AC平分∠DAB；‎ ‎（2）求证：△PCF是等腰三角形；‎ ‎（3）若tan∠ABC=，BE=7，求线段PC的长．‎ 解答：‎ 解：（1）∵PD切⊙O于点C，‎ ‎∴OC⊥PD． ‎ 又∵AD⊥PD，‎ ‎∴OC∥AD．‎ ‎∴∠ACO=∠DAC．‎ 又∵OC=OA，‎ ‎∴∠ACO=∠CAO，‎ ‎∴∠DAC=∠CAO，‎ 即AC平分∠DAB．‎ ‎（2）∵AD⊥PD，‎ ‎∴∠DAC+∠ACD=90°．‎ 又∵AB为⊙O的直径，‎ ‎∴∠ACB=90°．‎ ‎∴∠PCB+∠ACD=90°，‎ ‎∴∠DAC=∠PCB．‎ 又∵∠DAC=∠CAO，‎ ‎∴∠CAO=∠PCB．‎ ‎∵CE平分∠ACB，‎ ‎∴∠ACF=∠BCF，‎ ‎∴∠CAO+∠ACF=∠PCB+∠BCF，‎ ‎∴∠PFC=∠PCF，‎ ‎∴PC=PF，‎ ‎∴△PCF是等腰三角形．‎ ‎（3）连接AE．‎ ‎∵CE平分∠ACB，‎ ‎∴=，‎ ‎∴．‎ ‎∵AB为⊙O的直径，‎ ‎∴∠AEB=90°．‎ 在Rt△ABE中，． ‎ ‎∵∠PAC=∠PCB，∠P=∠P，‎ ‎∴△PAC∽△PCB，‎ ‎∴．‎ 又∵tan∠ABC=，‎ ‎∴，‎ ‎∴．‎ 设PC=4k，PB=3k，则在Rt△POC中，PO=3k+7，OC=7，‎ ‎∵PC2+OC2=OP2，‎ ‎∴（4k）2+72=（3k+7）2，‎ ‎∴k=6 （k=0不合题意，舍去）．‎ ‎∴PC=4k=4×6=24．‎ ‎3、（2015•黄陂区校级模拟）如图，点P在y轴的正半轴上，⊙P交x轴于B、C两点，以AC为直角边作等腰Rt△ACD，BD分别交y轴和⊙P于E、F两点，交连接AC、FC．‎ ‎（1）求证：∠ACF=∠ADB；‎ ‎（2）若点A到BD的距离为m，BF+CF=n，求线段CD的长；‎ ‎（3）当⊙P的大小发生变化而其他条件不变时，的值是否发生变化？若不发生变化，请求出其值；若发生变化，请说明理由．‎ 解答：‎ ‎（1）证明：连接AB，‎ ‎∵OP⊥BC，‎ ‎∴BO=CO，‎ ‎∴AB=AC，‎ 又∵AC=AD，‎ ‎∴AB=AD，‎ ‎∴∠ABD=∠ADB，‎ 又∵∠ABD=∠ACF，‎ ‎∴∠ACF=∠ADB． ‎ ‎（2）解：过点A作AM⊥CF交CF的延长线于M，过点A作AN⊥BF于N，连接AF，‎ 则AN=m，‎ ‎∴∠ANB=∠AMC=90°，‎ 在△ABN和△ACM中 ‎，‎ ‎∴Rt△ABN≌Rt△ACM（AAS）‎ ‎∴BN=CM，AN=AM，‎ 又∵∠ANF=∠AMF=90°，‎ 在Rt△AFN和Rt△AFM中 ‎，‎ ‎∴Rt△AFN≌Rt△AFM（HL），‎ ‎∴NF=MF，‎ ‎∴BF+CF=BN+NF+CM﹣MF，‎ ‎=BN+CM=2BN=n，‎ ‎∴BN=，‎ ‎∴在Rt△ABN中，AB2=BN2+AN2=m2+=m2+，‎ 在Rt△ACD中，CD2=AB2+AC2=2AB2=2m2+，‎ ‎∴CD=． ‎ ‎（3）解：的值不发生变化，‎ 过点D作DH⊥AO于N，过点D作DQ⊥BC于Q， ‎ ‎∵∠DAH+∠OAC=90°，∠DAH+∠ADH=90°，‎ ‎∴∠OAC=∠ADH，‎ 在△DHA和△AOC中 ‎，‎ ‎∴Rt△DHA≌Rt△AOC（AAS），‎ ‎∴DH=AO，AH=OC，‎ 又∵BO=OC，‎ ‎∴HO=AH+AO=OB+DH，‎ 而DH=OQ，HO=DQ，‎ ‎∴DQ=OB+OQ=BQ，‎ ‎∴∠DBQ=45°，‎ 又∵DH∥BC，‎ ‎∴∠HDE=45°，‎ ‎∴△DHE为等腰直角三角形，‎ ‎∴=，‎ ‎∴=．‎ ‎4、（2013•成都模拟）已知：如图，在半径为4的⊙O中，AB，CD是两条直径，M为OB的中点，CM的延长线交⊙O于点E，且EM＞MC．连接DE，DE=．‎ ‎（1）求证：AM•MB=EM•MC；‎ ‎（2）求sin∠EOB的值；‎ ‎（3）若P是直径AB延长线上的点，且BP=12，求证：直线PE是⊙O的切线．‎ 解答：‎ 解：（1）连接AE，BC，‎ ‎∵∠AEC与∠MBC都为所对的圆周角，‎ ‎∴∠AEC=∠MBC，又∠AME=∠BMC（对顶角相等），‎ ‎∴△AME∽△CMB，‎ ‎∴AM：CM=EM：MB，即AM•MB=EM•MC；‎ ‎（2）如图，∵DC为⊙O的直径，‎ ‎∴DE⊥EC，‎ ‎∵DC=8，DE=，‎ ‎∴EC===7，‎ 设EM=x，由于M为OB的中点，‎ ‎∴BM=2，AM=6，‎ ‎∴AM•MB=x•（7﹣x），即6×2=x（7﹣x），‎ 整理得：x2﹣7x+12=0，‎ 解得：x1=3，x2=4，‎ ‎∵EM＞MC，∴EM=4，‎ ‎∵OE=EM=4，‎ ‎∴△OEM为等腰三角形，‎ 过E作EF⊥OM，垂足为F，则OF=OM=1，‎ ‎∴EF===，‎ ‎∴sin∠EOB=；‎ ‎（3）在Rt△EFP中，EF=，PF=FB+BP=3+12=15，‎ 根据勾股定理得：EP===4，‎ 又OE=4，OP=OB+BP=4+12=16，‎ ‎∴OE2+EP2=16+240=256，OP2=256，‎ ‎∴OE2+EP2=OP2，‎ ‎∴∠OEP=90°，‎ 则EP为圆O的切线．‎ ‎5、（2012•杭州）如图，AE切⊙O于点E，AT交⊙O于点M，N，线段OE交AT于点C，OB⊥AT于点B，已知∠EAT=30°，AE=3，MN=2．‎ ‎（1）求∠COB的度数；‎ ‎（2）求⊙O的半径R；‎ ‎（3）点F在⊙O上（是劣弧），且EF=5，把△OBC经过平移、旋转和相似变换后，使它的两个顶点分别与点E，F重合．在EF的同一侧，这样的三角形共有多少个？你能在其中找出另一个顶点在⊙O上的三角形吗？请在图中画出这个三角形，并求出这个三角形与△OBC的周长之比．‎ 解答：‎ 解：（1）∵AE切⊙O于点E，‎ ‎∴AE⊥CE，又OB⊥AT，‎ ‎∴∠AEC=∠CBO=90°，‎ 又∠BCO=∠ACE，‎ ‎∴△AEC∽△OBC，又∠A=30°，‎ ‎∴∠COB=∠A=30°；‎ ‎（2）∵AE=3，∠A=30°，‎ ‎∴在Rt△AEC中，tanA=tan30°=，即EC=AEtan30°=3，‎ ‎∵OB⊥MN，∴B为MN的中点，又MN=2，‎ ‎∴MB=MN=，‎ 连接OM，在△MOB中，OM=R，MB=，‎ ‎∴OB==，‎ 在△COB中，∠BOC=30°，‎ ‎∵cos∠BOC=cos30°==，‎ ‎∴BO=OC，‎ ‎∴OC=OB=，‎ 又OC+EC=OM=R，‎ ‎∴R=+3，‎ 整理得：R2+18R﹣115=0，即（R+23）（R﹣5）=0，‎ 解得：R=﹣23（舍去）或R=5，‎ 则R=5；‎ ‎（3）以EF为斜边，有两种情况，以EF为直角边，有四种情况，所以六种，‎ 画直径FG，连接EG，延长EO与圆交于点D，连接DF，如图所示：‎ ‎∵EF=5，直径ED=10，可得出∠FDE=30°，‎ ‎∴FD=5，‎ 则C△EFD=5+10+5=15+5，‎ 由（2）可得C△COB=3+，‎ ‎∴C△EFD：C△COB=（15+5）：（3+）=5：1．‎ ‎∵EF=5，直径FG=10，可得出∠FGE=30°，‎ ‎∴EG=5，‎ 则C△EFG=5+10+5=15+5，‎ ‎∴C△EFG：C△COB=（15+5）：（3+）=5：1．‎ ‎6、（2011•潍坊）如图，AB是半圆O的直径，AB=2．射线AM、BN为半圆O的切线．在AM上取一点D，连接BD交半圆于点C，连接AC．过O点作BC的垂线OE，垂足为点E，与BN相交于点F．过D点作半圆O的切线DP，切点为P，与BN相交于点Q．‎ ‎（1）求证：△ABC∽△OFB；‎ ‎（2）当△ABD与△BFO的面枳相等时，求BQ的长；‎ ‎（3）求证：当D在AM上移动时（A点除外），点Q始终是线段BF的中点．‎ ‎．‎ 解答：‎ ‎（1）证明：∵AB为直径，‎ ‎∴∠ACB=90°，即：AC⊥BC，‎ 又OE⊥BC，‎ ‎∴OE∥AC，‎ ‎∴∠BAC=∠FOB，‎ ‎∵BN是半圆的切线，‎ ‎∴∠BCA=∠FBO=90°，‎ ‎∴△ABC∽△OFB．‎ ‎（2）解：由△ACB∽△OBF得，∠OFB=∠DBA，∠BCA=∠FBO=90°，‎ ‎∵AM、BN是⊙O的切线，‎ ‎∴∠DAB=∠OBF=90°，‎ ‎∴△ABD∽△BFO，‎ ‎∴当△ABD与△BFO的面积相等时，△ABD≌△BFO，‎ ‎∴AD=OB=1，‎ ‎∵DP切圆O，DA切圆O，‎ ‎∴DP=DA，‎ ‎∵△ABD≌△BFO，‎ ‎∴DA=BO=PO=DP，‎ 又∵∠DAO=∠DPO=90°，‎ ‎∴四边形AOPD是正方形，‎ ‎∴DQ∥AB，‎ ‎∴四边形ABQD是矩形，‎ ‎∴BQ=AD=1；‎ ‎（3）证明：由（2）知，△ABD∽△BFO，‎ ‎∴=，‎ ‎∴BF===，‎ ‎∵DP是半圆O的切线，射线AM、BN为半圆O的切线，‎ ‎∴AD=DP，QB=QP，‎ 过Q点作AM的垂线QK，垂足为K，在Rt△DQK中，‎ DQ2=QK2+DK2，‎ ‎∴（AD+BQ）2=（AD﹣BQ）2+22．‎ ‎∴BQ=，‎ ‎∴BF=2BQ，‎ ‎∴Q为BF的中点．‎ 专题二、三角函数在圆中的应用 ‎1、（2014成都）如图，在圆O的内接ΔABC中，∠ACB=90°，AC=2BC,过C作AB的垂线l交圆O于另一点D，垂足为E，P为弧上异于A、C的一个动点，射线AP交l于点F，连接PC与PD，PD交AB与点C。‎ ‎（1）求证：ΔPAC∽ΔPDF；‎ ‎（2）若AB=5，=，求PD的长；‎ ‎（3）在点P运动过程中，设，tan∠AFD=y，求y与x之间的函数关系式。（不要求写出x的取值范围）‎ 解：（1）同弧所对的圆周角相等∠PAC=∠PDC,∠AFD=∠ABP=∠ACP,∴ΔPAC∽ΔPDF；‎ ‎（2）=且AB为直径；∴ΔAPB为等腰直角三角形；‎ 又∵AB=5，AC=2BC；∴；‎ ‎∴由射影定理可得DE=CE=2，BE=1，AE=4；‎ 又∵∠APB=∠AEF=90°；∴∠AFE=∠ABP=45°；∴FE=AE=4；‎ 由（1）的相似可得,即,∴。‎ ‎（3）如图，过点G作GH┴PB于点H，‎ ‎∵；‎ ‎∴；‎ 又∵=；∴∠HPG=∠CAB；‎ ‎∴‎ ‎∴y与x之间的函数关系式为.‎ ‎2、（2012•襄阳）如图，PB为⊙O的切线，B为切点，直线PO交⊙于点E、F，过点B作PO的垂线BA，垂足为点D，交⊙O于点A，延长AO与⊙O交于点C，连接BC，AF．‎ ‎（1）求证：直线PA为⊙O的切线；‎ ‎（2）试探究线段EF、OD、OP之间的等量关系，并加以证明；‎ ‎（3）若BC=6，tan∠F=，求cos∠ACB的值和线段PE的长．‎ 解答：‎ 解：（1）连接OB，‎ ‎∵PB是⊙O的切线，‎ ‎∴∠PBO=90°，‎ ‎∵OA=OB，BA⊥PO于D，‎ ‎∴AD=BD，∠POA=∠POB，‎ 又∵PO=PO，‎ ‎∴△PAO≌△PBO（SAS），‎ ‎∴∠PAO=∠PBO=90°，‎ ‎∴OA⊥PA，‎ ‎∴直线PA为⊙O的切线．‎ ‎（2）EF2=4OD•OP．‎ 证明：∵∠PAO=∠PDA=90°‎ ‎∴∠OAD+∠AOD=90°，∠OPA+∠AOP=90°，‎ ‎∴∠OAD=∠OPA，‎ ‎∴△OAD∽△OPA，‎ ‎∴=，即OA2=OD•OP，‎ 又∵EF=2OA，‎ ‎∴EF2=4OD•OP．‎ ‎（3）∵OA=OC，AD=BD，BC=6，‎ ‎∴OD=BC=3（三角形中位线定理），‎ 设AD=x，‎ ‎∵tan∠F=，‎ ‎∴FD=2x，OA=OF=2x﹣3，‎ 在Rt△AOD中，由勾股定理，得（2x﹣3）2=x2+32，‎ 解之得，x1=4，x2=0（不合题意，舍去），‎ ‎∴AD=4，OA=2x﹣3=5，‎ ‎∵AC是⊙O直径，‎ ‎∴∠ABC=90°，‎ 又∵AC=2OA=10，BC=6，‎ ‎∴cos∠ACB==．‎ ‎∵OA2=OD•OP，‎ ‎∴3（PE+5）=25，‎ ‎∴PE=．‎ ‎3、（2014•武侯区校级自主招生）如图，⊙O与直线PC相切于点C，直径AB∥PC，PA交⊙O于D，BP交⊙O于E，DE交PC于F．‎ ‎（1）求证：PF2=EF•FD；‎ ‎（2）当tan∠APB=，tan∠ABE=，AP=时，求PF的长；‎ ‎（3）在（2）条件下，连接BD，判断△ADB是什么三角形？并证明你的结论．‎ Rt△．‎ 解答：‎ 解：（1）∵AB∥PC，‎ ‎∴∠BPC=∠ABE=∠ADE．‎ 又∵∠PFE=∠DFP，△PFE∽△DFP，‎ ‎∴PF：EF=DF：PF，PF2=EF•FD．‎ ‎（2）连接AE，‎ ‎∵AB为直径，‎ ‎∴AE⊥BP．‎ ‎∵tan∠APB==，tan∠ABE==，‎ 令AE=a，PE=2a，BE=3a，AP=a=，‎ ‎∴a==AE，PE=，BE=．‎ ‎∵PC为切线，‎ ‎∴PC2=PE•PB=4．‎ ‎∴PC=2．‎ ‎∵FC2=FE•FD=PF2∴PF=FC==1，‎ ‎∴PF=1．‎ ‎（3）△ADB为等腰直角三角形．‎ ‎∵AB为直径，‎ ‎∴∠ADB=90°．‎ ‎∵PE•PB=PA•PD，‎ ‎∴PD=2BD===AD．‎ ‎∴△ADB为等腰Rt△．‎ ‎4、（2014•盘锦）如图，△ABC中，∠C=90°，点G是线段AC上的一动点（点G不与A、C重合），以AG为直径的⊙O交AB于点D，直线EF垂直平分BD，垂足为F，EF交BC于点E，连结DE．‎ ‎（1）求证：DE是⊙O的切线；‎ ‎（2）若cosA=，AB=8，AG=2，求BE的长；‎ ‎（3）若cosA=，AB=8，直接写出线段BE的取值范围．‎ 解答：‎ ‎（1）证明：连接OD，如图，‎ ‎∵△ABC中，∠C=90°，‎ ‎∴∠A+∠B=90°，‎ ‎∵直线EF垂直平分BD，‎ ‎∴ED=EB，‎ ‎∴∠B=∠EDB，‎ ‎∵OA=OD，‎ ‎∴∠A=∠ODA，‎ ‎∴∠ODA+∠EDB=90°，‎ ‎∴∠ODE=90°，‎ ‎∴OD⊥DE，‎ ‎∴DE是⊙O的切线；‎ ‎（2）解：连接GD，‎ ‎∵AG为直径，‎ ‎∴∠ADG=90°，‎ ‎∵cosA=，‎ ‎∴∠A=60°，‎ ‎∴∠AGD=30°，‎ ‎∴AD=AG=，‎ ‎∵AB=8，‎ ‎∴BD=AB﹣AD=8﹣=7，‎ ‎∵直线EF垂直平分BD，‎ ‎∴BF=BD=，‎ 在Rt△BEF中，∠B=30°，‎ ‎∴EF=BF=，‎ ‎∴BE=2EF=7；‎ ‎（3）解：∵cosA=，‎ ‎∴∠A=60°，‎ ‎∴∠B=30°，‎ ‎∴AC=AB=4，‎ 由（2）得AD=AG，‎ BF=（AB﹣AD）=4﹣AG，‎ 在Rt△BEF中，∠B=30°，‎ ‎∴EF=BF，‎ ‎∴BE=2EF=BF=（4﹣AG）=8﹣AG，‎ ‎∵0＜AG＜AC，即0＜AG＜4，‎ ‎∴6＜BE＜8．‎ 专题三、相似三角形与圆的综合应用 ‎1、（略）‎ ‎2、（2014•镇江）如图，⊙O的直径AC与弦BD相交于点F，点E是DB延长线上的一点，∠EAB=∠ADB．‎ ‎（1）求证：EA是⊙O的切线；‎ ‎（2）已知点B是EF的中点，求证：以A、B、C为顶点的三角形与△AEF相似；‎ ‎（3）已知AF=4，CF=2．在（2）条件下，求AE的长．‎ 解答：‎ ‎（1）证明：如图1，连接CD，‎ ‎∵AC是⊙O的直径，‎ ‎∴∠ADC=90°，‎ ‎∴∠ADB+∠EDC=90°，‎ ‎∵∠BAC=∠EDC，∠EAB=∠ADB，‎ ‎∴∠EAC=∠EAB+∠BAC=90°，‎ ‎∴EA是⊙O的切线．‎ ‎（2）证明：如图2，连接BC，‎ ‎∵AC是⊙O的直径，‎ ‎∴∠ABC=90°，‎ ‎∴∠CBA=∠ABC=90°‎ ‎∵B是EF的中点，‎ ‎∴在RT△EAF中，AB=BF，‎ ‎∴∠BAC=∠AFE，‎ ‎∴△EAF∽△CBA．‎ ‎（3）解：∵△EAF∽△CBA，‎ ‎∴=，‎ ‎∵AF=4，CF=2．‎ ‎∴AC=6，EF=2AB，‎ ‎∴=，解得AB=2．‎ ‎∴EF=4，‎ ‎∴AE===4，‎ ‎3、（2013•桂林）如图，在△ABC中，∠C=90°，∠BAC的平分线AD交BC于D，过点D作DE⊥AD交AB于E，以AE为直径作⊙O．‎ ‎（1）求证：点D在⊙O上；‎ ‎（2）求证：BC是⊙O的切线；‎ ‎（3）若AC=6，BC=8，求△BDE的面积．‎ 解答：‎ ‎（1）证明：连接OD，‎ ‎∵△ADE是直角三角形，OA=OE，‎ ‎∴OD=OA=OE，‎ ‎∴点D在⊙O上；‎ ‎（2）证明：∵AD是∠BAC的角平分线，‎ ‎∴∠CAD=∠DAB，‎ ‎∵OD=OA，‎ ‎∴∠OAD=∠ODA，‎ ‎∴∠CAD=∠ODA，‎ ‎∴AC∥OD，‎ ‎∴∠C=∠ODB=90°，‎ ‎∴BC是⊙O的切线；‎ ‎（3）解：在Rt△ACB中，AC=6，BC=8，‎ ‎∴根据勾股定理得：AB=10，‎ 设OD=OA=OE=x，则OB=10﹣x，‎ ‎∵AC∥OD，△ACB∽△ODB，‎ ‎∴==，即=，‎ 解得：x=，‎ ‎∴OD=，BE=10﹣2x=10﹣=，‎ ‎∵=，即=，‎ ‎∴BD=5，‎ 过E作EH⊥BD，‎ ‎∵EH∥OD，‎ ‎∴△BEH∽△BOD，‎ ‎∴=，即=，‎ ‎∴EH=，‎ ‎∴S△BDE=BD•EH=．‎ ‎4、（2012•泰州）如图，已知直线l与⊙O相离，OA⊥l于点A，OA=5．OA与⊙O相交于点P，AB与⊙O相切于点B，BP的延长线交直线l于点C．‎ ‎（1）试判断线段AB与AC的数量关系，并说明理由；‎ ‎（2）若PC=2，求⊙O的半径和线段PB的长；‎ ‎（3）若在⊙O上存在点Q，使△QAC是以AC为底边的等腰三角形，求⊙O的半径r的取值范围．‎ 解答：‎ 解：（1）AB=AC，理由如下：‎ 连接OB．‎ ‎∵AB切⊙O于B，OA⊥AC，‎ ‎∴∠OBA=∠OAC=90°，‎ ‎∴∠OBP+∠ABP=90°，∠ACP+∠APC=90°，‎ ‎∵OP=OB，‎ ‎∴∠OBP=∠OPB，‎ ‎∵∠OPB=∠APC，‎ ‎∴∠ACP=∠ABC，‎ ‎∴AB=AC；‎ ‎（2）延长AP交⊙O于D，连接BD，‎ 设圆半径为r，则OP=OB=r，PA=5﹣r，‎ 则AB2=OA2﹣OB2=52﹣r2，‎ AC2=PC2﹣PA2=﹣（5﹣r）2，‎ ‎∴52﹣r2=﹣（5﹣r）2，‎ 解得：r=3，‎ ‎∴AB=AC=4，‎ ‎∵PD是直径，‎ ‎∴∠PBD=90°=∠PAC，‎ 又∵∠DPB=∠CPA，‎ ‎∴△DPB∽△CPA，‎ ‎∴=，‎ ‎∴=，‎ 解得：PB=．‎ ‎∴⊙O的半径为3，线段PB的长为；‎ ‎（3）作出线段AC的垂直平分线MN，作OE⊥MN，则可以推出OE=AC=AB=‎ 又∵圆O与直线MN有交点，‎ ‎∴OE=≤r，‎ ‎≤2r，‎ ‎25﹣r2≤4r2，‎ r2≥5，‎ ‎∴r≥，‎ 又∵圆O与直线相离，‎ ‎∴r＜5，‎ 即≤r＜5．‎ ‎5、（2012•德阳）如图，已知点C是以AB为直径的⊙O上一点，CH⊥AB于点H，过点B作⊙O的切线交直线AC于点D，点E为CH的中点，连接AE并延长交BD于点F，直线CF交AB的延长线于G．‎ ‎（1）求证：AE•FD=AF•EC；‎ ‎（2）求证：FC=FB；‎ ‎（3）若FB=FE=2，求⊙O的半径r的长．‎ 解答：‎ ‎（1）证明：∵BD是⊙O的切线，‎ ‎∴∠DBA=90°，‎ ‎∵CH⊥AB，‎ ‎∴CH∥BD，‎ ‎∴△AEC∽△AFD，‎ ‎∴=，‎ ‎∴AE•FD=AF•EC．‎ ‎（2）证明：连接OC，BC，‎ ‎∵CH∥BD，‎ ‎∴△AEC∽△AFD，△AHE∽△ABF，‎ ‎∴=，=，‎ ‎∴==，‎ ‎∵CE=EH（E为CH中点），‎ ‎∴BF=DF，‎ ‎∵AB为⊙O的直径，‎ ‎∴∠ACB=∠DCB=90°，‎ ‎∵BF=DF，‎ ‎∴CF=DF=BF（直角三角形斜边上的中线等于斜边的一半），‎ 即CF=BF．‎ ‎（3）解：∵BF=CF=DF（已证），EF=BF=2，‎ ‎∴EF=FC，‎ ‎∴∠FCE=∠FEC，‎ ‎∵∠AHE=∠CHG=90°，‎ ‎∴∠FAH+∠AEH=90°，∠G+∠GCH=90°，‎ ‎∵∠AEH=∠CEF，‎ ‎∴∠G=∠FAG，‎ ‎∴AF=FG，‎ ‎∵FB⊥AG，‎ ‎∴AB=BG，‎ ‎∵BF切⊙O于B，‎ ‎∴∠FBC=∠CAB，‎ ‎∵OC=OA，CF=BF，‎ ‎∴∠FCB=∠FBC，∠OCA=∠OAC，‎ ‎∴∠FCB=∠CAB，‎ ‎∵∠ACB=90°，‎ ‎∴∠ACO+∠BCO=90°，‎ ‎∴∠FCB+∠BCO=90°，‎ 即OC⊥CG，‎ ‎∴CG是⊙O切线，‎ ‎∵GBA是⊙O割线，AB=BG（已证），‎ FB=FE=2，‎ ‎∴由切割线定理得：（2+FG）2=BG×AG=2BG2，‎ 在Rt△BFG中，由勾股定理得：BG2=FG2﹣BF2，‎ ‎∴FG2﹣4FG﹣12=0，‎ 解得：FG=6，FG=﹣2（舍去），‎ 由勾股定理得：‎ AB=BG==4，‎ ‎∴⊙O的半径是2．‎ ‎6、（略）‎ ‎7、（略）‎ ‎8、（2004•武汉）已知：如图，直线y=kx+3（k＞0）交x轴于B点，交y轴于A点，以A为圆心，AB为半径作⊙A交x轴于另一点D，交y轴于E、F两点，交直线AB于C点，连接BE、CE，∠CBD的平分线交CE于I点．‎ ‎（1）求证：BE=IE；‎ ‎（2）若AI⊥CE，设Q为弧BF上一点，连接DQ交y轴于T，连接BQ并延长交y轴于G点，求AT•AG的值；‎ ‎（3）设P为线段AB上的一个动点（异于A、B），连接PD交y轴于M点，过P、M、B三点作⊙O1交y轴于另一点N．设⊙O1的半径为R，当时，给出下列两个结论：①MN的长度不变；②的值不变，其中有且只有一个结论是正确的，请你判断哪一个结论正确，证明正确的结论并求出其值．‎ 解答：‎ ‎（1）证明：∵AE⊥BD，‎ ‎∴弧BE=弧DE．‎ ‎∴∠1=∠2．‎ ‎∵∠3=∠4，∠5=∠2+∠3，∠IBE=∠1+∠4，‎ ‎∴∠5=∠IBE．‎ ‎∴BE=IE．‎ ‎（2）解：连接QC、TB，‎ 则∠6+∠CBQ=90°，‎ 又∠7+∠8=90°，而∠6=∠7，‎ ‎∴∠CBQ=∠8=∠9．‎ ‎∴△ABG∽△ATB．‎ ‎∴AB2=AG•AT．‎ ‎∵AI⊥CE，‎ ‎∴I为CE的中点．‎ ‎∴AE=AC，IE=IC．‎ ‎∴△BEO∽△CBE．‎ ‎∴OE：OB=BE：CE=1：2．‎ 设⊙A的半径为R，‎ 由AB2﹣OA2=BO2，OE=R﹣3，‎ 得R2﹣32=4（R﹣3）2‎ 解得R=5，或R=3（不合题意，舍去）．‎ ‎∴AT•AG=AB2=25．‎ ‎（方法二提示：可连接AD、CD证△BAG∽△TAD）‎ ‎（3）解：②的值不变．‎ 证明：作O1K⊥MN于K，连接O1N、PN、BM，‎ 则MN=2NK，且∠N O1K=∠1，‎ ‎∴==2sin∠NO1K=2sin∠1‎ 由直线y=x+3得OB=OD=4，OM⊥BD，‎ ‎∴∠2=∠3．‎ 又∠2=∠4+∠5，∠3=∠1+∠6，‎ ‎∵∠5=∠6，‎ ‎∴∠1=∠4=∠NO1K，=2sin∠4=2×=．‎ 所以的值不变，其值为．‎ 专题四、圆中的面积问题 ‎1、(1)如图，连接DO并延长交圆于点E，连接AE ‎∵DE是直径，∴∠DAE=90°，‎ ‎∴∠E+∠ADE=90°‎ ‎∵∠PDA=∠ADB=∠E ‎∴∠PDA+∠ADE=90°即PD⊥DO ‎∴PD与圆O相切于点D ‎(2) ∵tan∠ADB=‎ ‎∴可设AH=3k,则DH=4k ‎∵‎ ‎∴PA=‎ ‎∴PH=‎ ‎∴∠P=30°，∠PDH=60°‎ ‎∴∠BDE=30°‎ 连接BE，则∠DBE=90°，DE=2r=50‎ ‎∴BD=DE·cos30°=‎ ‎(3)由（2）知，BH=-4k，∴HC=(-4k)‎ 又∵‎ ‎∴‎ 解得k=‎ ‎∴AC=‎ ‎∴S=‎ ‎28．（1） ‎ ‎（2）M的坐标是（1-，--2）、（1+，-2）、（4，-1）、（2，-3）、（-2，-7）‎ ‎（3）的最大值是/‎ ‎2、（2013•钦州）如图，在Rt△ABC中，∠A=90°，O是BC边上一点，以O为圆心的半圆与AB边相切于点D，与AC、BC边分别交于点E、F、G，连接OD，已知BD=2，AE=3，tan∠BOD=．‎ ‎（1）求⊙O的半径OD；‎ ‎（2）求证：AE是⊙O的切线；‎ ‎（3）求图中两部分阴影面积的和．‎ 解答：‎ 解：（1）∵AB与圆O相切，‎ ‎∴OD⊥AB，‎ 在Rt△BDO中，BD=2，tan∠BOD==，‎ ‎∴OD=3；‎ ‎（2）连接OE，‎ ‎∵AE=OD=3，AE∥OD，‎ ‎∴四边形AEOD为平行四边形，‎ ‎∴AD∥EO，‎ ‎∵DA⊥AE，‎ ‎∴OE⊥AC，‎ 又∵OE为圆的半径，‎ ‎∴AE为圆O的切线；‎ ‎（3）∵OD∥AC，‎ ‎∴=，即=，‎ ‎∴AC=7.5，‎ ‎∴EC=AC﹣AE=7.5﹣3=4.5，‎ ‎∴S阴影=S△BDO+S△OEC﹣S扇形FOD﹣S扇形EOG ‎=×2×3+×3×4.5﹣‎ ‎=3+﹣‎ ‎=．‎ ‎3略 ‎4略 ‎5略 ‎6略 专题五、中点在圆中的应用、‎ ‎1、略 ‎2、（2014•长沙）如图，以△ABC的一边AB为直径作⊙O，⊙O与BC边的交点恰好为BC的中点D，过点D作⊙O的切线交AC于点E．‎ ‎（1）求证：DE⊥AC；‎ ‎（2）若AB=3DE，求tan∠ACB的值．‎ 解答：‎ ‎（1）证明：连接OD，‎ ‎∵D是BC的中点，OA=OB，‎ ‎∴OD是△ABC的中位线，‎ ‎∴OD∥AC，‎ ‎∵DE是⊙O的切线，‎ ‎∴OD⊥DE，‎ ‎∴DE⊥AC；‎ ‎（2）解：连接AD，‎ ‎∵AB是⊙O的直径，‎ ‎∴∠ADB=90°，‎ ‎∵DE⊥AC，‎ ‎∴∠ADC=∠DEC=∠AED=90°，‎ ‎∴∠ADE=∠DCE 在△ADE和△CDE中，‎ ‎∴△CDE∽△DAE，‎ ‎∴，‎ 设tan∠ACB=x，CE=a，则DE=ax，AC=3ax，AE=3ax﹣a，‎ ‎∴，整理得：x2﹣3x+1=0，‎ 解得：x=，‎ ‎∴tan∠ACB=或．‎ ‎（可以看出△ABC分别为锐角、钝角三角形两种情况）‎ ‎3、014•广安）如图，AB为⊙O的直径，以AB为直角边作Rt△ABC，∠CAB=90°，斜边BC与⊙O交于点D，过点D作⊙O的切线DE交AC于点E，DG⊥AB于点F，交⊙O于点G．‎ ‎（1）求证：E是AC的中点；‎ ‎（2）若AE=3，cos∠ACB=，求弦DG的长．‎ 解答：‎ ‎（1）证明：连AD，如图 ‎∵AB为⊙O的直径，∠CAB=90°，‎ ‎∴AC是⊙O的切线，‎ 又∵DE与⊙O相切，‎ ‎∴ED=EA，‎ ‎∴∠EAD=∠EDA，‎ 而∠C=90°﹣∠EAD，∠CDE=90°﹣∠EDA，‎ ‎∴∠C=∠CDE，‎ ‎∴ED=EC，‎ ‎∴EA=EC，‎ 即E为AC的中点；‎ ‎（2）解：由（1）知，E为AC的中点，则AC=2AE=6．‎ ‎∵cos∠ACB=，‎ 设AC=2x，BC=3x，‎ 根据勾股定理，得AB==（3x）2﹣（2x）2=x，‎ ‎∴sin∠ACB=．‎ 连接AD，则∠ADC=90°，‎ ‎∴∠ACB+∠CAD=90°，‎ ‎∵∠CAD+∠DAF=90°，‎ ‎∴∠DAF=∠ACB，‎ 在Rt△ACD中，AD=AC•sin∠ACB=6×=．‎ 在Rt△ADF中，DF=AD•sin∠DAF=AD•sin∠ACB=×=，‎ ‎∴DG=2DF=．‎ ‎4略 ‎5、（2011•广州）如图1，⊙O中AB是直径，C是⊙O上一点，∠ABC=45°，等腰直角三角形DCE中∠DCE是直角，点D在线段AC上．‎ ‎（1）证明：B、C、E三点共线；‎ ‎（2）若M是线段BE的中点，N是线段AD的中点，证明：MN=OM；‎ ‎（3）将△DCE绕点C逆时针旋转α（0°＜α＜90°）后，记为△D1CE1（图2），若M1是线段BE1的中点，N1是线段AD1的中点，M1N1=OM1是否成立？若是，请证明；若不是，说明理由．‎ 解答：‎ ‎（1）证明：∵AB是直径，‎ ‎∴∠BCA=90°，‎ 而等腰直角三角形DCE中∠DCE是直角，‎ ‎∴∠BCA+∠DCE=90°+90°=180°，‎ ‎∴B、C、E三点共线；‎ ‎（2）连接BD，AE，ON，延长BD交AE于F，如图1，‎ ‎∵CB=CA，CD=CE，‎ ‎∴Rt△BCD≌Rt△ACE，‎ ‎∴BD=AE，∠EBD=∠CAE，‎ ‎∴∠CAE+∠ADF=∠CBD+∠BDC=90°，即BF⊥AE，‎ 又∵M是线段BE的中点，N是线段AD的中点，而O为AB的中点，‎ ‎∴ON=BD，OM=AE，ON∥BD，AE∥OM；‎ ‎∴ON=OM，ON⊥OM，即△ONM为等腰直角三角形，‎ ‎∴MN=OM；‎ ‎（3）成立．‎ 理由如下：如图2，连接BD1，AE1，ON1，‎ ‎∵∠ACB﹣∠ACD1=∠D1CE1﹣∠ACD1，‎ ‎∴∠BCD1=∠ACE1，‎ 又∵CB=CA，CD1=CE1，‎ ‎∴△BCD1≌△ACE1，‎ 与（2）同理可证BD1⊥AE1，△ON1M1为等腰直角三角形，‎ 从而有M1N1=OM1．‎ ‎6、　‎ ‎14．（2011•金华）如图，在平面直角坐标系中，点A（10，0），以OA为直径在第一象限内作半圆C，点B是该半圆周上一动点，连接OB、AB，并延长AB至点D，使DB=AB，过点D作x轴垂线，分别交x轴、直线OB于点E、F，点E为垂足，连接CF．‎ ‎（1）当∠AOB=30°时，求弧AB的长度；‎ ‎（2）当DE=8时，求线段EF的长；‎ ‎（3）在点B运动过程中，是否存在以点E、C、F为顶点的三角形与△AOB相似？若存在，请求出此时点E的坐标；若不存在，请说明理由．‎ 解答：‎ 解：（1）连接BC，‎ ‎∵A（10，0），∴OA=10，CA=5，‎ ‎∵∠AOB=30°，‎ ‎∴∠ACB=2∠AOB=60°，‎ ‎∴弧AB的长=；（4分）‎ ‎（2）①若D在第一象限，‎ 连接OD，‎ ‎∵OA是⊙C直径，‎ ‎∴∠OBA=90°，‎ 又∵AB=BD，‎ ‎∴OB是AD的垂直平分线，‎ ‎∴OD=OA=10，‎ 在Rt△ODE中，‎ OE==，‎ ‎∴AE=AO﹣OE=10﹣6=4，‎ 由∠AOB=∠ADE=90°﹣∠OAB，∠OEF=∠DEA，‎ 得△OEF∽△DEA，‎ ‎∴，即，‎ ‎∴EF=3；（4分）‎ ‎②若D在第二象限，‎ 连接OD，‎ ‎∵OA是⊙C直径，‎ ‎∴∠OBA=90°，‎ 又∵AB=BD，‎ ‎∴OB是AD的垂直平分线，‎ ‎∴OD=OA=10，‎ 在Rt△ODE中，‎ OE==，‎ ‎∴AE=AO+OE=10+6=16，‎ 由∠AOB=∠ADE=90°﹣∠OAB，∠OEF=∠DEA，‎ 得△OEF∽△DEA，‎ ‎∴，即=，‎ ‎∴EF=12；‎ ‎∴EF=3或12；‎ ‎（3）设OE=x，‎ ‎①当交点E在O，C之间时，由以点E、C、F为顶点的三角 形与△AOB相似，有∠ECF=∠BOA或∠ECF=∠OAB，‎ 当∠ECF=∠BOA时，此时△OCF为等腰三角形，点E为OC 中点，即OE=，‎ ‎∴E1（，0）；‎ 当∠ECF=∠OAB时，有CE=5﹣x，AE=10﹣x，‎ ‎∴CF∥AB，有CF=，‎ ‎∵△ECF∽△EAD，‎ ‎∴，即，解得：，‎ ‎∴E2（，0）；‎ ‎②当交点E在点C的右侧时，‎ ‎∵∠ECF＞∠BOA，‎ ‎∴要使△ECF与△BAO相似，只能使∠ECF=∠BAO，‎ 连接BE，‎ ‎∵BE为Rt△ADE斜边上的中线，‎ ‎∴BE=AB=BD，‎ ‎∴∠BEA=∠BAO，‎ ‎∴∠BEA=∠ECF，‎ ‎∴CF∥BE，‎ ‎∴，‎ ‎∵∠ECF=∠BAO，∠FEC=∠DEA=90°，‎ ‎∴△CEF∽△AED，‎ ‎∴，‎ 而AD=2BE，‎ ‎∴，‎ 即，解得，＜0（舍去），‎ ‎∴E3（，0）；‎ ‎③当交点E在点O的左侧时，‎ ‎∵∠BOA=∠EOF＞∠ECF．‎ ‎∴要使△ECF与△BAO相似，只能使∠ECF=∠BAO 连接BE，得BE==AB，∠BEA=∠BAO ‎∴∠ECF=∠BEA，‎ ‎∴CF∥BE，‎ ‎∴，‎ 又∵∠ECF=∠BAO，∠FEC=∠DEA=90°，‎ ‎∴△CEF∽△AED，‎ ‎∴，‎ 而AD=2BE，‎ ‎∴，‎ ‎∴，‎ 解得x1=，x2=，‎ ‎∵点E在x轴负半轴上，‎ ‎∴E4（，0），‎ 综上所述：存在以点E、C、F为顶点的三角形与△AOB相似，‎ 此时点E坐标为：E1（，0）、E2（，0）、E3（，0）、E4（，0）．（4分）‎