中考数学复习试卷初三期末复习卷一

中考数学复习试卷初三期末复习卷一

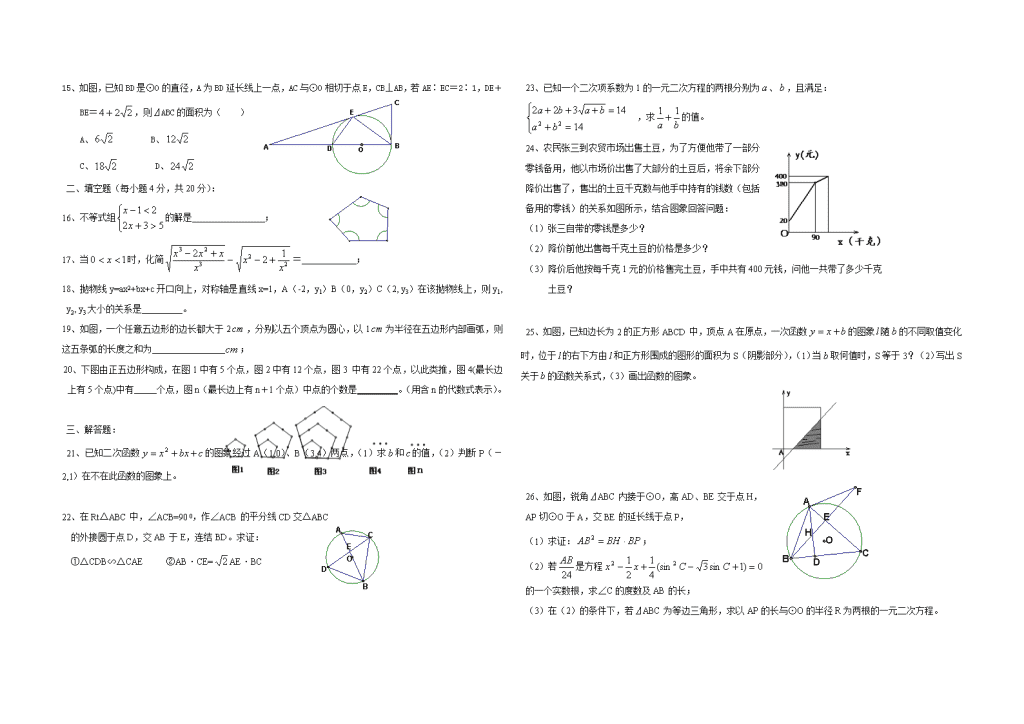
初三期末复习卷（一）‎ 一、选择题（每小题3分，共45分）：‎ ‎1、下列运算正确的是（　　）‎ ‎　A、　　　B、　　C、　D、　‎ ‎2、当前我国的道路交通安全形势十分严峻，据公安部统计，2004年我国交通事故死亡人数为107077人，居世界第一，这个数用科学记数法表示（保留三个有效数字）是（　　）‎ ‎　A、　　　B、　　　C、　　　D、‎ ‎3、如图，在⊿ABC中，D、E分别是AB、AC的中点，‎ 且AB＝10，AC＝8，BC＝12，则DE的长是（　　）‎ ‎　A、5　　　B、4　　　C、9　　　D、6‎ ‎4、已知两圆半径分别为2和7，且两圆相交，则圆心距的取值范围是（　　）‎ ‎　A、　　　B、　　　C、　　　D、‎ ‎5、已知、是方程的两根，则的值是（　　）‎ ‎　A、15　　　　B、－13　　　　C、　　　　D、‎ ‎6、下列命题中，属于假命题的是（　　）‎ ‎　A、函数的图象与轴有公共点 ‎　B、中，S和成正比例 ‎　C、在函数中，当时，随的增大而增大 ‎　D、函数的图象是一条抛物线 ‎7、抛物线是由抛物线经过平移而得到的，则正确的平移是（　　）‎ ‎　A、先向右平移1个单位，再向下平移2个单位 ‎　B、先向左平移1个单位，再向上平移2个单位 ‎　C、先向右平移2个单位，再向下平移1个单位 ‎　D、先向左平移2个单位，再向上平移1个单位 ‎8、已知一次函数的图象经过点P（3,4），则图象一定经过点Q（，）的一次函数是（　　）‎ ‎　A、　　B、　　C、　　D、‎ ‎9、当时，点P（，）在（　　）‎ ‎　A、第一象限　　　B、第二象限　　C、第三象限　　D、第四象限 ‎10、关于的一元二次方程有实数根，则的范围是（　　）‎ ‎　A、　　　B、　　　C、且　　　D、且 ‎11、学生佳佳家距学校有公里路程，她骑自行车以匀速上学，半路上车子坏了，她就以匀速步行到校，共用时间小时，下列能大致表示佳佳距学校（公里）与离家时间（小时）之间关系的图象是（　　）‎ ‎12、某商场推出如下优惠销售方法：（1）一次性购物不超过100元，不享受优惠；（2）一次性购物超过100元但不超过300元，一律九折；（3）一次性购物超过300元，一律八折。陈红两次购物分别付款80元和252元，如果陈红一次购买与上面两次相同的商品，比分两次购买可节约（　　）‎ A、16元　　　　B、79元或72元　　　　C、44元　　　D、16元或44元 ‎13、如图，在⊿ABC中，∠C＝，BC＝12，AB的中 垂线MN交BC于D，连结AD，若，则 AC的长是（　　）‎ ‎　A、6　　　B、9　　　C、12　　　D、15‎ ‎14、直线与坐标轴交于A、B两点，C在坐标轴上，⊿ABC为等腰三角形，则满足条件的点C有（　　）‎ ‎　A、8个　　　B、7个　　　C、5个　　　D、4个 ‎15、如图，已知BD是⊙O的直径，A为BD延长线上一点，AC与⊙O相切于点E，CB⊥AB，若AE∶EC＝2∶1，DE＋BE＝，则⊿ABC的面积为（　　）‎ ‎　　A、　　　　B、　　　　‎ C、　　　　D、‎ 二、填空题（每小题4分，共20分）：‎ ‎16、不等式组的解是　　　　　　　　；‎ ‎17、当时，化简＝　　　　　　；‎ ‎18、抛物线y=ax2+bx+c开口向上，对称轴是直线x=1，A（-2，y1）B（0，y2）C（2, y3）在该抛物线上，则y1, y2, y3大小的关系是_________。‎ ‎19、如图，一个任意五边形的边长都大于2，分别以五个顶点为圆心，以1为半径在五边形内部画弧，则这五条弧的长度之和为　　　　　　　　；‎ ‎20、下图由正五边形构成，在图1中有5个点，图2中有12个点，图3 中有22个点，以此类推，图4(最长边上有5个点)中有 个点，图n（最长边上有n＋1个点）中点的个数是_________。（用含n的代数式表示）。‎ 三、解答题：‎ ‎21、已知二次函数的图象经过A（1,0）、B（3,4）两点，（1）求和的值，（2）判断P（－2,1）在不在此函数的图象上。‎ ‎22、在Rt△ABC中，∠ACB=900，作∠ACB的平分线CD交△ABC 的外接圆于点D，交AB于E，连结BD。求证：‎ ‎①△CDB∽△CAE ②AB·CE=AE·BC ‎23、已知一个二次项系数为1的一元二次方程的两根分别为、，且满足：‎ ‎　，求的值。‎ ‎24、农民张三到农贸市场出售土豆，为了方便他带了一部分 零钱备用，他以市场价出售了大部分的土豆后，将余下部分 降价出售了，售出的土豆千克数与他手中持有的钱数（包括 备用的零钱）的关系如图所示，结合图象回答问题：‎ ‎（1）张三自带的零钱是多少？‎ ‎（2）降价前他出售每千克土豆的价格是多少？‎ ‎（3）降价后他按每千克1元的价格售完土豆，手中共有400元钱，问他一共带了多少千克 土豆？‎ ‎25、如图，已知边长为2的正方形ABCD中，顶点A在原点，一次函数的图象随的不同取值变化时，位于的右下方由和正方形围成的图形的面积为S（阴影部分），（1）当取何值时，S等于3？（2）写出S关于的函数关系式，（3）画出函数的图象。‎ ‎26、如图，锐角⊿ABC内接于⊙O，高AD、BE交于点H，‎ AP切⊙O于A，交BE的延长线于点P，‎ ‎（1）求证：；‎ ‎（2）若是方程 的一个实数根，求∠C的度数及AB的长；‎ ‎（3）在（2）的条件下，若⊿ABC为等边三角形，求以AP的长与⊙O的半径R为两根的一元二次方程。‎ 初三期末复习卷（一）答案 一、选择题（每小题3分，共45分）：‎ ‎ 1－5　CCDBC　　6－10　DABBC　　11－15　DDAAB 二、填空题（每小题4分，共20分）：‎ ‎　　16、　17、 18、 19、 20、35，。‎ 三、解答题：‎ ‎21、解：（1）将点A（1,0）、B（3,4）的坐标分别代入得：‎ ‎　　　　　………………………………………………………2分 ‎　　　　解得：　　…………………………………………………4分 ‎　　　　（2）由（1）知函数解析式为：‎ ‎　　　　把代入解析式得：　……………………6分 ‎　　　　所以点P（－2,1）不在此函数的图象上。………………………………7分 ‎22、证明：（1）∵CD是∠ACB的平分线 ‎∴∠ACE=∠DCB　………………………2分 又∵∠A=∠D ‎∴⊿CDB∽⊿CAE　　………………………4分 ‎（2）∵由（1）知：⊿CDB∽⊿CAE ‎∴ ……………………………5分 连结AD　∵∠ACE＝∠DCB ‎∴AD＝DB　　……………………………………………6分 又∵AB是直径　∴⊿ABD是等腰直角三角形 ‎∴AB＝BD　　…………………………………………………………7分 ‎∴ 即 　　…………………8分 ‎23、解：将方程组变形为：‎ ‎　　……………………………………………………2分 解（1）式得：（舍去）或 ‎∴　　………………………………………………………………………5分 代入（2）得：‎ ‎∴　　……………………………………7分 ‎∴ 　………………………8分 ‎24、解：（1）由图象可知，张三自带零钱是20元；…………3分 ‎　　　（2）因为出售土豆‎90千克，张三共得了360元钱，‎ ‎　　　　　所以降价前张三出售土豆的价格是每千克4元；………………………6分 ‎　　　（3）因为降价出售的土豆共得20元钱，价格是每千克1元，所以张三出售的土豆共 有‎20千克，因此，张三一共带了‎110千克土豆。………………………10分 ‎25、解：（1）因为当直线过原点时，正好是正方形对角线所在直线，这时阴影部分面积为2，‎ ‎　　　　　因此这时直线与轴的交点在轴上方，所以有 ‎　　　　　　　　…………………………………………………………1分 解得：　　…………………………………………………………2分 由题意取 即等于时，阴影部分面积为3。………3分 ‎（2）当≤－2时，S＝0　　……………………………………………………4分 ‎　　　　　　当≤0时，S＝　………………………………………5分 ‎　　　　　　当时，S＝　……………………………………6分 ‎　　　　　　当≥2时，S＝4‎ ‎ 　……………………………………7分 ‎　　　　（3）图像略　　…………………………………………………………10分 ‎26、（1）证明：∵AD⊥BC，BE⊥AC ‎∴∠BAD与∠ABD互余，∠P与∠EAP互余　…………1分 又∵AP是切线 ∴∠ABD=∠EAP ‎∴∠BAD=∠P　………………………………2分 又∵∠ABH公共 ∴⊿ABH∽⊿PBA　………3分 即 即 ………………4分 ‎（2）∵是方程的根 ‎∴⊿＝‎ ‎　　＝≥0　　…………………………………………5分 ‎∴　　∴∠C＝　…………………………………………6分 这时方程为：　…………………………………………7分 将代入可得：‎ ‎∴AB＝6　　………………………………………………………………………10分 ‎（3）∵AB＝6　∴　AD＝　　　　AP＝6‎ ‎∴所求方程为：‎ ‎　　即　　　…………………………12分