中考数学阅读理解专题复习

中考数学阅读理解专题复习

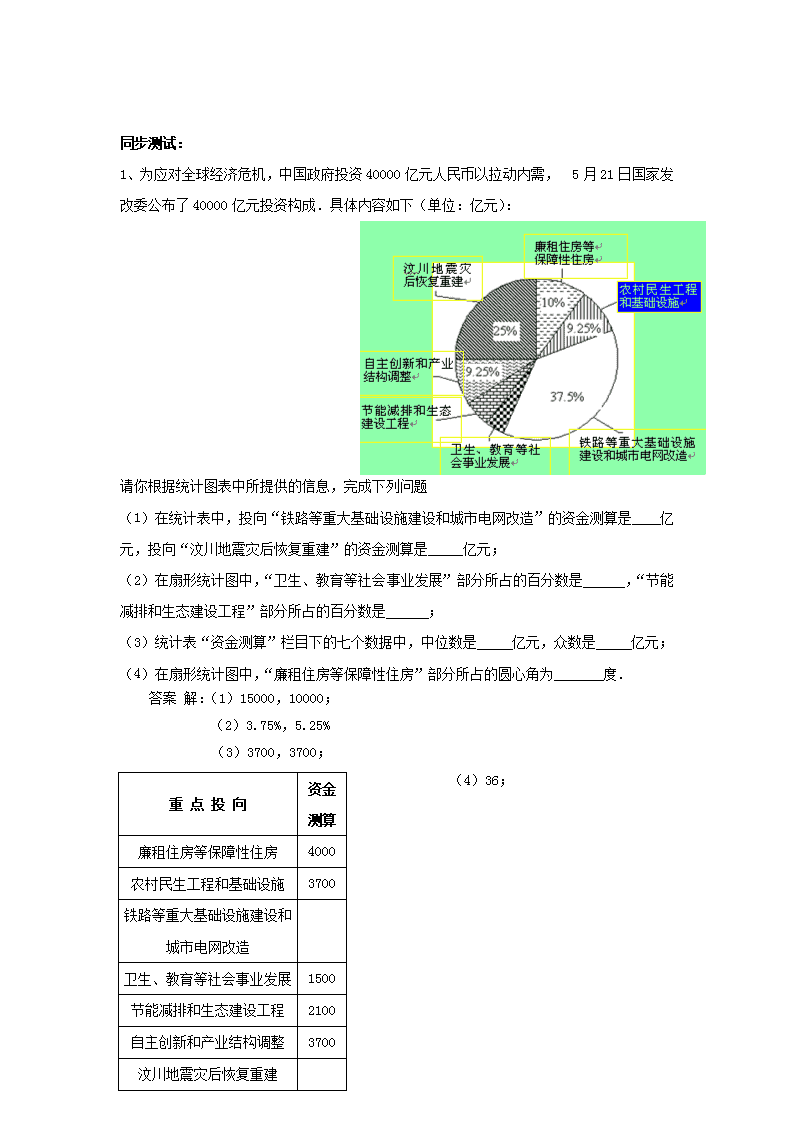
阅读理解 一、阅读给定材料，理解概念公式 例1、宽与长的比是的矩形叫黄金矩形．心理测试表明：黄金矩形令人赏心悦目，它给我们以协调，匀称的美感．现将小波同学在数学活动课中，折叠黄金矩形的方法归纳如下（如图1所示）：‎ A B C D E F M N 图1‎ 第一步：作一个正方形ABCD；‎ 第二步：分别取AD，BC的中点M，N，连接MN；‎ 第三步：以N为圆心，ND长为半径画弧，交BC的延长线于E；‎ 第四步：过E作EF⊥AD，交AD的延长线于F．‎ 请你根据以上作法，证明矩形DCEF为黄金矩形．‎ 证明：在正方形ABCD中，取，‎ ‎∵ N为BC的中点，‎ ‎∴ ． ‎ 在中，‎ ‎． ‎ 又∵ ，‎ ‎∴ ． ‎ ‎∴ ．‎ 故矩形DCEF为黄金矩形． ‎ 同步测试：‎ ‎1、对于任意两个实数对（a，b）和（c，d），规定：当且仅当a＝c且b＝d时， ‎ ‎（a，b）=（c，d）．定义运算“”：（a，b）（c，d）=（ac－bd，ad＋bc）．‎ 若（1，2）（p，q）=（5，0），则p＝ ，q＝ ．(答案：1，–2)‎ ‎2、先阅读下列材料，然后解答问题：‎ 从三张卡片中选两张，有三种不同选法，抽象成数学问题就是从3个元素中选取2个元素组合，记作．‎ 一般地，从个元素中选取个元素组合，记作：‎ 例：从7个元素中选5个元素，共有种不同的选法．‎ 问题：从某学习小组10人中选取3人参加活动，不同的选法共有 种．（答案：120）‎ 二、阅读表格图像，提取有用信息 例2、某饮料厂为了开发新产品，用种果汁原料和种果汁原料试制新型甲、乙两种饮料共‎50千克，设甲种饮料需配制千克，两种饮料的成本总额为元．‎ ‎（1）已知甲种饮料成本每千克4元，乙种饮料成本每千克3元，请你写出与之间的函数关系式．‎ ‎（2）若用‎19千克种果汁原料和‎17.2千克种果汁原料试制甲、乙两种新型饮料，下表是试验的相关数据；‎ 每千克饮料果汁含量 果汁 甲 乙 A ‎0.5千克 ‎0.2千克 B ‎0.3千克 ‎0.4千克 请你列出关于且满足题意的不等式组，求出它的解集，并由此分析如何配制这两种饮料，可使值最小，最小值是多少？‎ 解：（1）依题意得： ‎ ‎（2）依题意得： ‎ 解不等式（1）得： ‎ 解不等式（2）得：‎ 不等式组的解集为 ‎ ‎，是随的增大而增大，且 当甲种饮料取28千克，乙种饮料取22千克时，‎ 成本总额最小，（元） ‎ 同步测试：‎ ‎1、为应对全球经济危机，中国政府投资40000亿元人民币以拉动内需， ‎5月21日国家发改委公布了40000亿元投资构成．具体内容如下（单位：亿元）：‎ 重 点 投 向 资金 测算 廉租住房等保障性住房 ‎4000‎ 农村民生工程和基础设施 ‎3700‎ 铁路等重大基础设施建设和 城市电网改造 卫生、教育等社会事业发展 ‎1500‎ 节能减排和生态建设工程 ‎2100‎ 自主创新和产业结构调整 ‎3700‎ 汶川地震灾后恢复重建 请你根据统计图表中所提供的信息，完成下列问题 ‎（1）在统计表中，投向“铁路等重大基础设施建设和城市电网改造”的资金测算是 亿元，投向“汶川地震灾后恢复重建”的资金测算是 亿元；‎ ‎（2）在扇形统计图中，“卫生、教育等社会事业发展”部分所占的百分数是 ，“节能减排和生态建设工程”部分所占的百分数是 ；‎ ‎（3）统计表“资金测算”栏目下的七个数据中，中位数是 亿元，众数是 亿元；‎ ‎（4）在扇形统计图中，“廉租住房等保障性住房”部分所占的圆心角为 度．‎ 答案 解：（1）15000，10000； ‎ ‎（2）3.75%，5.25% ‎ ‎（3）3700，3700； ‎ ‎（4）36； ‎ 三、阅读例题解法，掌握思路方法 例3、阅读材料：把形如的二次三项式(或其一部分)配成完全平方式的方法叫做配方法. 配方法的基本形式是完全平方公式的逆写，即．‎ 例如：、是的三种不同形式的配方（即“余项”分别是常数项、一次项、二次项——见横线上的部分）．‎ 请根据阅读材料解决下列问题：‎ ‎（1）比照上面的例子，写出三种不同形式的配方；‎ ‎（2）将配方(至少两种形式)；‎ ‎（3）已知，求的值．‎ 解：（1）的配方（略）． ‎ ‎（2）． ‎ ‎（3）‎ ‎=． ‎ 从而． ‎ 即，，．‎ 所以 ‎ 同步测试：‎ ‎1、阅读下列材料，然后回答问题．‎ 在进行二次根式运算时，我们有时会碰上如一样的式子，其实我们还可以将其进一步化简：‎ ‎； （Ⅰ）‎ ‎ （Ⅱ）‎ ‎． （Ⅲ）‎ 以上这种化简的步骤叫做分母有理化．‎ 还可以用以下方法化简：‎ ‎． （Ⅳ）‎ ‎（1）请用不同的方法化简．‎ ‎①参照（Ⅲ）式得=___________________________________________．‎ ‎②参照（Ⅳ）式得=___________________________________________．‎ ‎（2）化简：．‎ 解：（1）①‎ ‎②‎ ‎（2）‎ 四、阅读特殊信息，归纳发现规律 例4、阅读材料，解答下列问题．‎ 例：当时，如则，故此时的绝对值是它本身 当时，，故此时的绝对值是零 当时，如则，故此时的绝对值是它的相反数 综合起来一个数的绝对值要分三种情况，即 这种分析方法涌透了数学的分类讨论思想．‎ 问：（1）请仿照例中的分类讨论的方法，分析二次根式的各种展开的情况．‎ ‎（2）猜想与的大小关系．‎ 解：（1）略 ‎ （2）=‎ 同步测试：‎ ‎1、，和分别可以按如图所示方式“分裂”成2个、3个和4个连续奇数的和，也能按此规律进行“分裂”，则“分裂”出的奇数中最大的是( A )‎ ‎9‎ ‎3‎ ‎5‎ ‎7‎ ‎11‎ ‎13‎ ‎15‎ ‎17‎ ‎19‎ A、41 B、39 ‎ C、31 D、29‎ ‎2、观察下列等式:‎ ① ‎32-12=4×2； ‎ ② ‎42-22=4×3；‎ ③ ‎52-32=4×4； ‎ ④ ‎（ ）2-（ ）2=（ ）×（ ）；‎ ‎……‎ 则第4个等式为_______． 第个等式为_____．（是正整数）‎ 答案：62-42=4×5（1分）；（n+2）2-n2=4×（n+1）．‎ 随堂检测：‎ ‎1、我们常用的数是十进制数，如，数要用10个数码（又叫数字）：0、1、2、3、4、5、6、7、8、9‎ ‎，在电子计算机中用的二进制，只要两个数码：0和1，如二进制中等于十进制的数6，等于十进制的数53．那么二进制中的数101011等于十进制中的哪个数？ ‎ ‎2、符号“”称为二阶行列式，规定它的运算法则为：，请你根据上述规定求出下列等式中的值．‎ ‎3、下面是按一定规律排列的一列数：‎ 第1个数：；‎ 第2个数：；‎ 第3个数：；‎ ‎……‎ 第个数：．‎ 那么，在第10个数、第11个数、第12个数、第13个数中，最大的数是（ ）‎ A．第10个数 B．第11个数 C．第12个数 D．第13个数 ‎4、先阅读理解下面的例题，再按要求解答：‎ 例题：解一元二次不等式.‎ 解：∵，‎ ‎∴.‎ 由有理数的乘法法则“两数相乘，同号得正”，有 ‎（1） （2）‎ 解不等式组（1），得，‎ 解不等式组（2），得，‎ 故的解集为或，‎ 即一元二次不等式的解集为或.‎ ‎ 问题：求分式不等式的解集.‎ ‎5、阅读下列材料，并解决后面的问题．‎ 材料：一般地，n个相同的因数相乘：．如23＝8，此时，3叫做以2为底8的对数，记为．‎ 一般地，若，则n叫做以为底b的对数，记为，则4叫做以3为底81的对数，记为．‎ ‎ 问题：（1）计算以下各对数的值： ‎ ‎ ．‎ ‎（2）观察（1）中三数4、16、64之间满足怎样的关系式？ 之间又满足怎样的关系式？（2分）‎ ‎（3）由（2）的结果，你能归纳出一个一般性的结论吗？ ‎ ‎ ‎ ‎（4）根据幂的运算法则：以及对数的含义证明上述结论．‎ ‎6、某家电商场计划用32400元购进“家电下乡”指定产品中的电视机、冰箱、洗衣机共15台．三种家电的进价和售价如下表所示：‎ 价格 种类 进价（元/台）‎ 售价（元/台）‎ 电视机 ‎2000‎ ‎2100‎ 冰箱 ‎2400‎ ‎2500‎ 洗衣机 ‎1600‎ ‎1700‎ ‎（1‎ ‎）在不超出现有资金的前提下，若购进电视机的数量和冰箱的数量相同，洗衣机数量不大于电视机数量的一半，商场有哪几种进货方案？‎ ‎（2）国家规定：农民购买家电后，可根据商场售价的13%领取补贴．在（1）的条件下，如果这15台家电全部销售给农民，国家财政最多需补贴农民多少元？‎ 随堂检测参考答案：‎ ‎1、解： ‎ ‎ ‎ ‎2、解：‎ ‎　整理得：2×－＝1‎ ‎＋＝1‎ 解之得：x　=　4‎ ‎3、答案：A ‎4、解：由有理数的除法法则“两数相除，同号得正”，有 ‎（1） （2）‎ 解不等式组（1），得，解不等式组（2），得无解，‎ 故分式不等式的解集为 ‎5、解：（1） ， ，‎ ‎（2）4×16＝64 ， ＋ ＝ ‎ ‎（3） ＋ ＝ ‎ ‎（4）证明：设＝b1 ， ＝b2‎ 则， ‎ ‎∴ ‎ ‎∴b1＋b2＝ 即 ＋ ＝ ‎ ‎6、设购进电视机、冰箱各x台，则洗衣机为（15-2x）台 ‎ 依题意得： ‎ 解这个不等式组，得6≤x≤7‎ ‎∵x为正整数，∴x=6或7 ‎ 方案1：购进电视机和冰箱各6台，洗衣机3台；‎ 方案2：购进电视机和冰箱各7台，洗衣机1台 ‎ ‎（2）方案1需补贴：（6×2100+6×2500+1×1700）×13%=4251（元）；‎ ‎ 方案2需补贴：（7×2100+7×2500+1×1700）×13%=4407（元）；‎ ‎∴国家的财政收入最多需补贴农民4407元. ‎