- 2021-05-10 发布 |
- 37.5 KB |
- 8页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
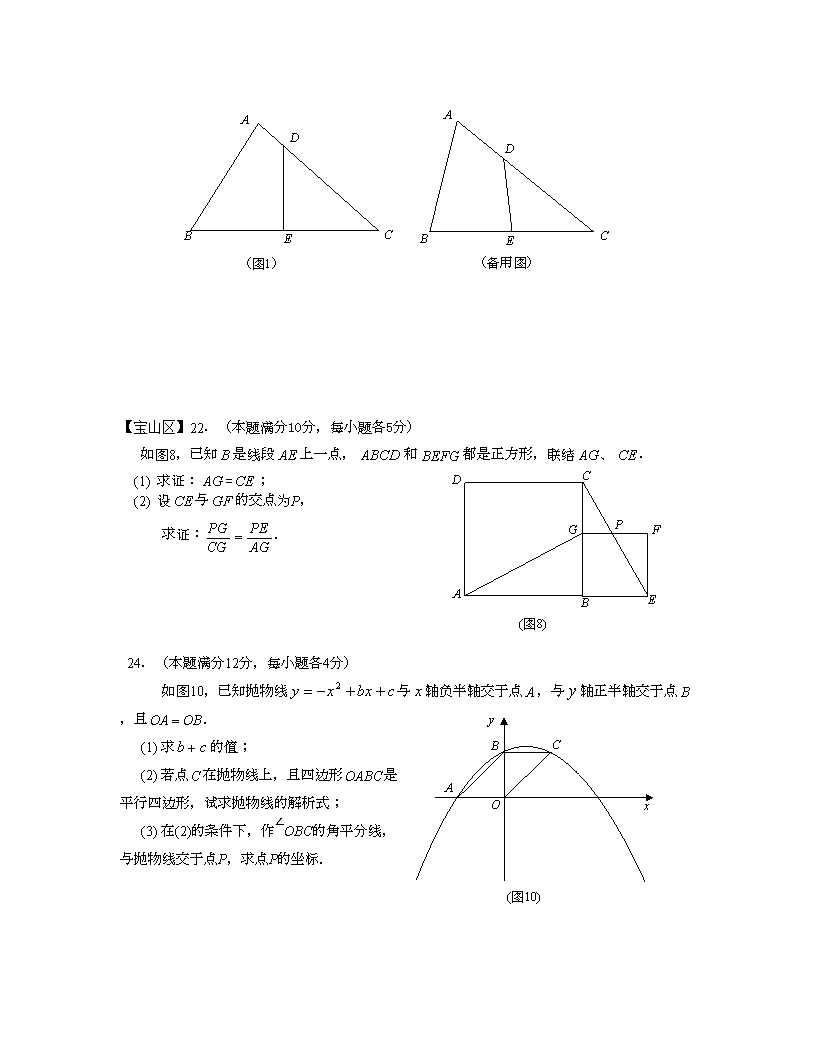
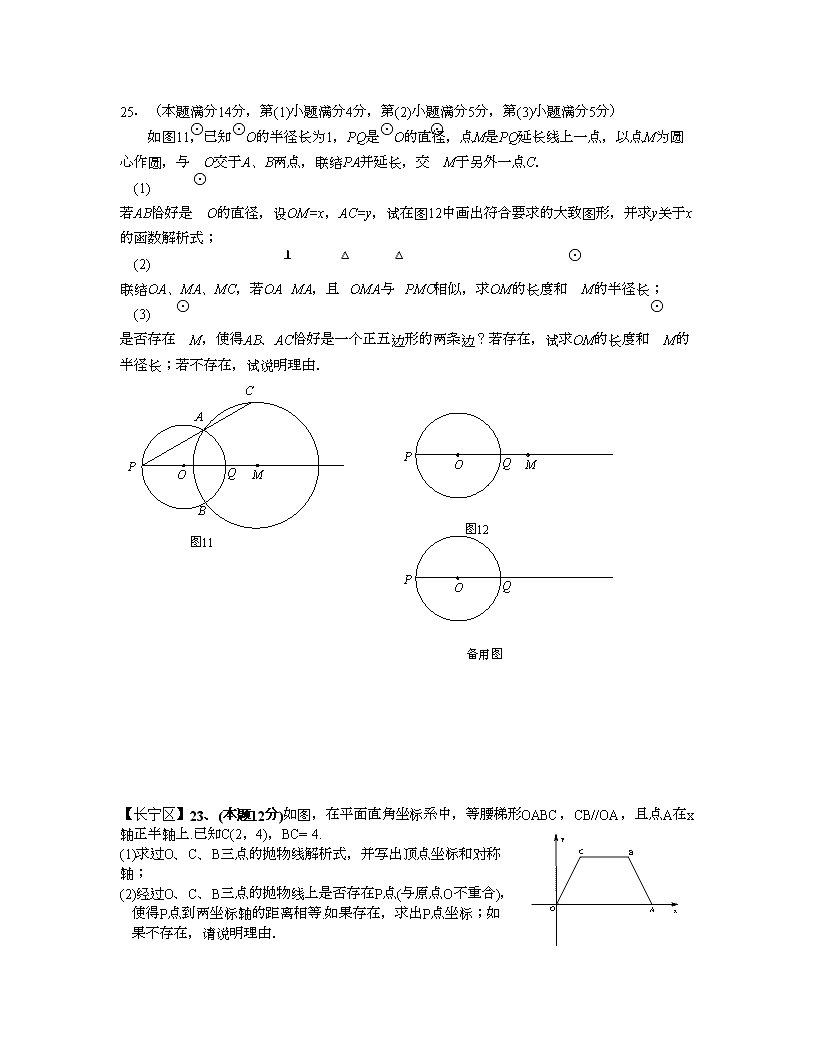
2011中考数学模拟复习精选题二
【杨浦区】23.(本题满分12分)如图,将矩形纸片折叠,使点落在边上的点处,折痕与AD边交于点E,与BC边交于点F,点A落在点处。 (1)请在图中作出示意图,其中折痕EF请用直尺和圆规作出,并保留作图痕迹; A B C D · (2)求证:; (3)设,试猜想之间的一种关系,并给予证明. O A B C D x y E 24.(本题满分12分)Rt△ABC在直角坐标系内的位置如图所示,反比例函数在第一象限内的图像与BC边交于点D(4,m),与AB边交于点E(2,n),△BDE的面积为2。 (1) 求m与n的数量关系; (2) 当tan∠A=时,求反比例函数的解析式和直线AB的表达式; (3) 设直线AB与y轴交于点F,点P在射线FD上,在(2)的条件下,如果△AEO与△EFP 相似,求点P的坐标。 25.(本题满分14分,第(1)小题4分,第(2)小题5分,第(3)小题5分) 已知△ABC中,AB=4,BC=6,AC>AB,点D为AC边上一点,且DC=AB,E为BC边的中点,联结DE,设AD=x。 (1) 当DE⊥BC时(如图1),求x的值; (2) 设,求y关于x的函数关系式,并写出定义域; (1) 取AD的中点M,联结EM并延长交BA的延长线于点P,以A为圆心AM为半径作⊙A,试问:当AD的长改变时,点P与⊙A的位置关系变化吗?若不变化,请说明具体的位置关系,并证明你的结论;若变化,请说明理由。 A B C D E (备用图) D C E B A (图1) 【宝山区】22.(本题满分10分,每小题各5分) A B C D E F G P (图8) 如图8,已知是线段上一点,和都是正方形,联结、. (1) 求证:=; (2) 设与的交点为P, 求证:. 24.(本题满分12分,每小题各4分) C B A O y x (图10) 如图10,已知抛物线与轴负半轴交于点,与轴正半轴交于点,且. (1) 求的值; (2) 若点在抛物线上,且四边形是 平行四边形,试求抛物线的解析式; (3) 在(2)的条件下,作∠OBC的角平分线, 与抛物线交于点P,求点P的坐标. 25.(本题满分14分,第(1)小题满分4分,第(2)小题满分5分,第(3)小题满分5分) 如图11,已知⊙O的半径长为1,PQ是⊙O的直径,点M是PQ延长线上一点,以点M为圆心作圆,与⊙O交于A、B两点,联结PA并延长,交⊙M于另外一点C. (1) 若AB恰好是⊙O的直径,设OM=x,AC=y,试在图12中画出符合要求的大致图形,并求y关于x的函数解析式; (2) 联结OA、MA、MC,若OA⊥MA,且△OMA与△PMC相似,求OM的长度和⊙M的半径长; (3) 是否存在⊙M,使得AB、AC恰好是一个正五边形的两条边?若存在,试求OM的长度和⊙M的半径长;若不存在,试说明理由. A B 图11 C Q P O M 图12 Q P O M 备用图 Q P O 【长宁区】23、(本题12分)如图,在平面直角坐标系中,等腰梯形OABC,CB//OA,且点A在x轴正半轴上.已知C(2,4),BC= 4. (1)求过O、C、B三点的抛物线解析式,并写出顶点坐标和对称轴; (2)经过O、C、B三点的抛物线上是否存在P点(与原点O不重合),使得P点到两坐标轴的距离相等.如果存在,求出P点坐标;如果不存在,请说明理由. 24、 (本题12分)如图,AD//BC,点E、F在BC上,∠1=∠2,AF⊥DE,垂足为点O. (1)求证:四边形AEFD是菱形; (2)若BE=EF=FC,求∠BAD+∠ADC的度数; (3)若BE=EF=FC,设AB = m,CD = n,求四边形ABCD的面积. 25、 (本题14分)如图,在平面直角坐标系中,抛物线与 x轴交于A、B两点(A点在B点左侧),与y轴交于C点,顶点为D.过点 C、D的直线与x轴交于E点,以OE为直径画⊙O1,交直线CD于P、E 两点. (1)求E点的坐标; (2)联结PO1、PA.求证:~; (3) ①以点O2 (0,m)为圆心画⊙O2,使得⊙O2与⊙O1相切, 当⊙O2经过点C时,求实数m的值; ②在①的情形下,试在坐标轴上找一点O3,以O3为圆心画 ⊙O3,使得⊙O3与⊙O1、⊙O2同时相切.直接写出满足条件的点O3的坐标(不需写出计算过程). 【金山区】23.(本题满分12分) D CA AA EA B 已知:如图,在中,°,是直角边的垂直平分线,,连接 求证:(1) 四边形是梯形 (2) 24.(本题满分12分)已知抛物线过点,,三点 (1)求抛物线的解析式; (2) 若抛物线的顶点为,求正切值; (3)若以、、、为顶点的四边形是平行四边形,求点的坐标. 25.(本题满分14分)如图,正方形的边长是,是的中点.动点在线段上运动.连接并延长交射线于点,过作的垂线交射线于点,连接、. (1)求证:是等腰三角形; (2)设时,的面积为.求关于的函数关系式,并写出自变量的取值范围; (3)在点运动过程中是否可以成为等边三角形?请说明理由. G M F E D C B A 【虹口区】23.(本题满分12分,第(1)小题6分,第(2)小题6分) A D E B F C 第23题图 OA 如图,EF是平行四边形ABCD的对角线BD的垂直平分线,EF与边AD、BC分别交于点E、F. (1)求证:四边形BFDE是菱形; (2)若E为线段AD的中点,求证:AB⊥BD. 24.(本题满分12分,第(1)小题6分,第(2)小题6分) 在平面直角坐标系中,抛物线经过点(0,2)和点(3,5). 1 2 3 4 1 2 3 4 -1 O 第24题图 -1 5 (1)求该抛物线的表达式并写出顶点坐标; (2)点P为抛物线上一动点,如果直径为4的 ⊙P与轴相切,求点P的坐标. 25.(本题满分14分,第(1)小题4分,第(2)小题5分,第(3)小题5分) 如图,在Rt△ABC中,∠BAC= 90°,AB=3,AC=4,AD是BC边上的高,点E、F分别是AB边和AC边上的动点,且∠EDF= 90°. (1)求DE︰DF的值; (2)联结EF,设点B与点E间的距离为,△DEF的面积为,求关于的函数解析式,并写出的取值范围; (3)设直线DF与直线AB相交于点G,△EFG能否成为等腰三角形?若能,请直接写出线段BE的长;若不能,请说明理由. A A 备用图1 B C D 第25题图 B C D E F A 备用图2 B C D 【静安区】 23.(本题满分12分,第(1)小题满分6分,第(2)小题满分6分) A B C D E G F H 已知:如图,在□ABCD中,点E、F分别是AB、CD的中点,CE、AF与对角线BD分别相交于点G、H. (1) 求证:DH=HG=BG; (2) 如果AD⊥BD,求证:四边形EGFH是菱形. (第23题图) A C B O x y 24.(本题满分12分,第(1)小题满分3分,第(2)小题满分9分) (第24题图) 如图, 二次函数的图像与轴、轴的交点分别为A、B,点C在这个二次函数的图像上,且∠ABC=90º,∠CAB=∠BAO,. (1)求点A的坐标; (2)求这个二次函数的解析式. 25.(本题满分14分,第(1)小题满分6分,第(2)小题满分5分,第(3)小题满分3分) B D C A O (第25题图) 如图,在半径为5的⊙O中,点A、B在⊙O上,∠AOB=90º,点C是AB上的一个动点,AC与OB的延长线相交于点D,设AC=,BD=. (1) 求关于的函数解析式,并写出它的定义域; (2) 如果⊙与⊙O相交于点A、C,且⊙与⊙O的圆心距为2,当BD=OB时,求⊙的半径; (3) 是否存在点C,使得△DCB∽△DOC?如果存在,请证明;如果不存在,请简要说明理由.查看更多