2007年上海市中考数学试卷

2007年上海市中考数学试卷

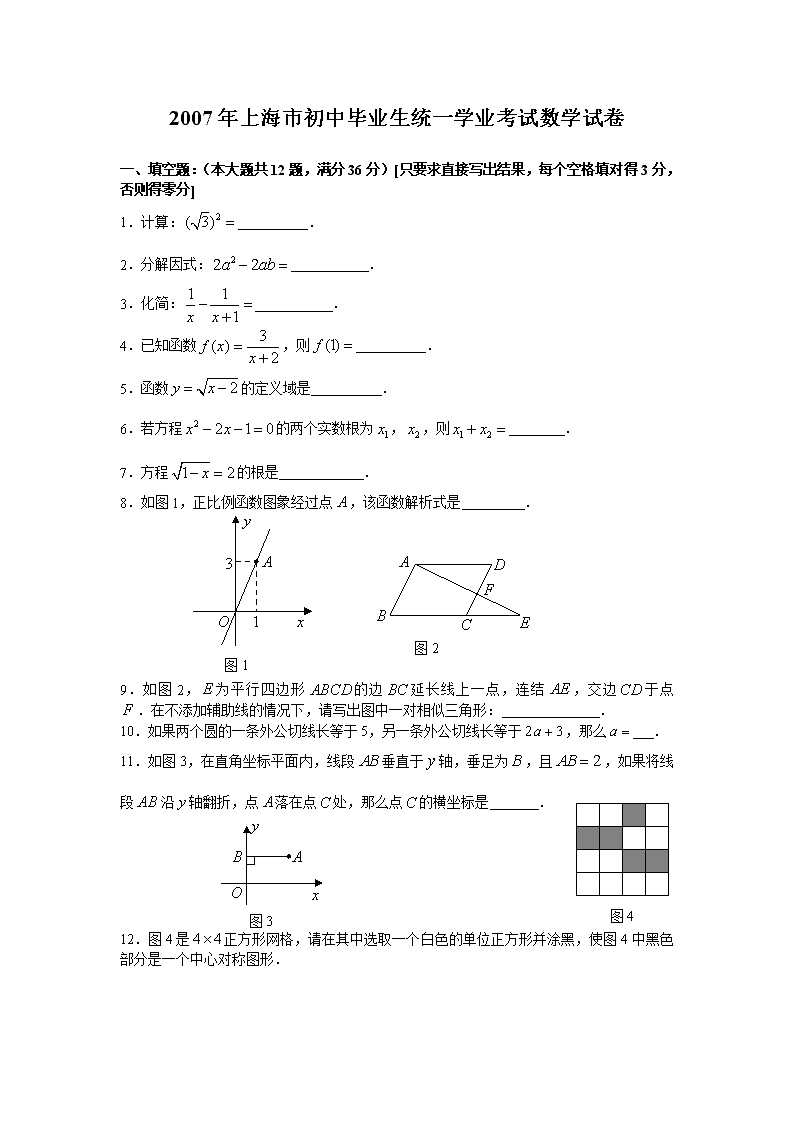
‎2007年上海市初中毕业生统一学业考试数学试卷 一、填空题：（本大题共12题，满分36分）[只要求直接写出结果，每个空格填对得3分，否则得零分]‎ ‎1．计算： ．‎ ‎2．分解因式： ．‎ ‎3．化简： ．‎ ‎4．已知函数，则 ．‎ ‎5．函数的定义域是 ．‎ ‎6．若方程的两个实数根为，，则 ．‎ ‎7．方程的根是 ．‎ ‎8．如图1，正比例函数图象经过点，该函数解析式是 ．‎ 图1‎ 图2‎ ‎9．如图2，为平行四边形的边延长线上一点，连结，交边于点．在不添加辅助线的情况下，请写出图中一对相似三角形： ．‎ ‎10．如果两个圆的一条外公切线长等于5，另一条外公切线长等于，那么 ．‎ 图4‎ 图3‎ ‎11．如图3，在直角坐标平面内，线段垂直于轴，垂足为，且，如果将线段沿轴翻折，点落在点处，那么点的横坐标是 ．‎ ‎12．图4是正方形网格，请在其中选取一个白色的单位正方形并涂黑，使图4中黑色部分是一个中心对称图形．‎ 二、选择题：（本大题共4题，满分16分）‎ ‎【下列各题的四个结论中，有且只有一个结论是正确的，把正确结论的代号写在题后的圆括号内，选对得4分；不选、错选或者多选得零分】‎ ‎13．在下列二次根式中，与是同类二次根式的是（ ）‎ A． B． C． D．‎ ‎14．如果一次函数的图象经过第一象限，且与轴负半轴相交，那么（ ）‎ A．， B．， C．， D．，‎ ‎15．已知四边形中，，如果添加一个条件，即可推出该四边形是正方形，那么这个条件可以是（ ）‎ A． B． C． D．‎ 图5‎ ‎16．小明不慎把家里的圆形玻璃打碎了，其中四块碎片如图5所示，为配到与原来大小一样的圆形玻璃，小明带到商店去的一块玻璃碎片应该是（ ）‎ A．第①块 B．第②块 C．第③块 D．第④块 三、（本大题共5题，满分48分）‎ ‎17．（本题满分9分）‎ 解不等式组：并把解集在数轴上表示出来．‎ ‎18．（本题满分9分）‎ 解方程：．‎ ‎19．（本题满分10分，第（1）小题满分6分，第（2）小题满分4分）‎ 图6‎ 如图6，在直角坐标平面内，为原点，点的坐标为，点在第一象限内，，．‎ 求：（1）点的坐标；（2）的值．‎ ‎20．（本题满分10分，第（1）小题满分4分，第（2），（3）小题满分各3分）‎ 初三学生小丽、小杰为了解本校初二学生每周上网的时间，各自在本校进行了抽样调查．小丽调查了初二电脑爱好者中40名学生每周上网的时间，算得这些学生平均每周上网时间为2.5小时；小杰从全体初二学生名单中随机抽取了40名学生，调查了他们每周上网的时间，算得这些学生平均每周上网时间为1.2小时．小丽与小杰整理各自样数据，如表一所示．请根据上述信息，回答下列问题：‎ ‎（1）你认为哪位学生抽取的样本具有代表性？答： ；‎ 估计该校全体初二学生平均每周上网时间为 小时；‎ ‎（2）根据具体代表性的样本，把图7中的频数分布直方图补画完整；‎ ‎（3）在具有代表性的样本中，中位数所在的时间段是 小时/周．‎ 图7‎ ‎（每组可含最低值，不含最高值）‎ ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ 小时/周 ‎2‎ ‎4‎ ‎6‎ ‎8‎ ‎10‎ ‎12‎ ‎14‎ ‎16‎ ‎18‎ ‎20‎ ‎22‎ 人数 时间段 ‎（小时／周）‎ 小丽抽样 人数 小杰抽样 人数 ‎0～1‎ ‎6‎ ‎22‎ ‎1～2‎ ‎10‎ ‎10‎ ‎2～3‎ ‎16‎ ‎6‎ ‎3～4‎ ‎8‎ ‎2‎ ‎（每组可含最低值，不含最高值）‎ 表一 ‎21．（本题满分10分）‎ ‎2001年以来，我国曾五次实施药品降价，累计降价的总金额为269亿元，五次药品降价的年份与相应降价金额如表二所示，表中缺失了2003年、2007年相关数据．已知2007年药品降价金额是2003年药品降价金额的6倍，结合表中信息，求2003年和2007年的药品降价金额．‎ 年份 ‎2001‎ ‎2003‎ ‎2004‎ ‎2005‎ ‎2007‎ 降价金额（亿元）‎ ‎54‎ ‎35‎ ‎40‎ 表二 四、（本大题共4题，满分50分）‎ ‎22．（本题满分12分，每小题满分各6分）‎ 在直角坐标平面内，二次函数图象的顶点为，且过点．‎ ‎（1）求该二次函数的解析式；‎ ‎（2）将该二次函数图象向右平移几个单位，可使平移后所得图象经过坐标原点？并直接写出平移后所得图象与轴的另一个交点的坐标．‎ ‎23．（本题满分12分，每小题满分各6分）‎ 如图8，在梯形中，，平分，，交的延长线于点，．‎ 图8‎ ‎（1）求证：；‎ ‎（2）若，，求边的长．‎ ‎24．（本题满分12分，每小题满分各4分）‎ 图9‎ 如图9，在直角坐标平面内，函数（，是常数）的图象经过，，其中．过点作轴垂线，垂足为，过点作轴垂线，垂足为，连结，，．‎ ‎（1）若的面积为4，求点的坐标；‎ ‎（2）求证：；‎ ‎（3）当时，求直线的函数解析式．‎ ‎25．（本题满分14分，第（1）小题满分4分，第（2），（3）小题满分各5分）‎ 已知：，点在射线上，（如图10）．为直线上一动点，以为边作等边三角形（点按顺时针排列），是的外心．‎ ‎（1）当点在射线上运动时，求证：点在的平分线上；‎ ‎（2）当点在射线上运动（点与点不重合）时，与交于点，设，，求关于的函数解析式，并写出函数的定义域；‎ ‎（3）若点在射线上，，圆为的内切圆．当的边或与圆相切时，请直接写出点与点的距离．‎ 图10‎ 备用图 ‎2007年上海市初中毕业生统一学业考试 数学试卷答案要点与评分标准 说明：‎ ‎1．解答只列出试题的一种或几种解法．如果考生的解法与所列解法不同，可参照解答中评分标准相应评分．‎ ‎2．第一大题只要求直接写出结果，每个空格填对得3分，否则得零分；第二大题每题选对得4分，不选、错选或者多选得零分；17题至25题中右端所注的分数，表示考生正确做对这一步应得分数，评分时，给分或扣分均以1分为单位．‎ 答案要点与评分标准 一、填空题（本大题共12题，满分36分）‎ ‎1．3 ‎ ‎2． ‎ 解：原式=2a（a-2b） ‎ ‎3． ‎ ‎ ‎ ‎4．1 ‎ ‎5． ‎ 解：根据题意得：x-2≥0，‎ 解得：x≥2． ‎ ‎6．2 ‎ 解：已知方程x的两个实数根为x1，x2；‎ ‎∴x1+x2=2．‎ 故本题答案为：2． ‎ ‎7．‎ 解：两边平方得，1-x=4，‎ 移项得：x=-3．‎ 故本题答案为：x=-3． ‎ ‎8． ‎ 解：设该正比例函数的解析式为y=kx，‎ 由图象可知，该函数图象过点A（1，3），‎ ‎∴3=k，‎ 即该正比例函数的解析式为y=3x． ‎ ‎9．（或，或） ‎ 解：∵四边形ABCD是平行四边形 ‎∴AD∥BC，AB∥CD ‎∴△AFD∽△EFC∽△EAB ‎10．1 ‎ 解：根据两条外公切线长是相等的，‎ ‎∴可知2a+3=5，‎ 解得a=1．‎ ‎11．‎ 解：根据题意，得两点关于y轴对称．则它们的横坐标互为相反数．即点C的横坐标是-2 ‎ ‎12．答案见图1‎ 图1‎ 二、选择题（本大题共4题，满分16分）‎ ‎13． C ‎14．B 解：由题意得，函数y=kx+b的图象经过第一、三、四象限，k＞0，b＜0．‎ 故选B． ‎ ‎15．D 解：由∠A=∠B=∠C=90°可判定为矩形，因此再添加条件：一组邻边相等，即可判定为正方形，故选D．‎ ‎16．B 解：第②块出现一段完整的弧，可在这段弧上任做两条弦，作出这两条弦的垂直平分线，就交于了圆心，进而可得到半径的长．‎ 故选B．‎ 三、（本大题共5题，满分48分）‎ ‎17．解：由，解得． 3分 由，解得． 3分 不等式组的解集是． 1分 解集在数轴上表示正确． 2分 ‎18．解：去分母，得， 3分 整理，得， 2分 解方程，得． 2分 经检验，是增根，是原方程的根，原方程的根是． 2分 ‎19．解：（1）如图2，作，垂足为， 1分 在中，，，‎ ‎． 2分 ‎．……………………………… 1分 图2‎ 点的坐标为．……………………2分 ‎（2），，．………………1分 在中，，．………… 1分 ‎．………………………………2分 ‎20．（1）小杰；1.2． 2分，2分 ‎（2）直方图正确． 3分 ‎（3）0~1． 3分 ‎21．解：[解法一]设2003年和2007年的药品降价金额分别为亿元、亿元． 1分 根据题意，得 解方程组，得 答：2003年和2007年的药品降价金额分别为20亿元和120亿元． 1分 ‎[解法二]设2003年的药品降价金额为亿元， 1分 则2007年的药品降价金额为亿元． 2分 根据题意，得． 2分 解方程，得，． 4分 答：2003年和2007年的药品降价金额分别为20亿元和120亿元． 1分 四、（本大题共4题，满分50分）‎ ‎22．解：（1）设二次函数解析式为， 2分 二次函数图象过点，，得． 3分 二次函数解析式为，即． 1分 ‎（2）令，得，解方程，得，． 2分 二次函数图象与轴的两个交点坐标分别为和．‎ 二次函数图象向右平移1个单位后经过坐标原点． 2分 平移后所得图象与轴的另一个交点坐标为． 2分 ‎23．（1）证明：，‎ ‎． 1分 平分，‎ ‎， 1分 ‎， 1分 又，‎ ‎． 1分 梯形是等腰梯形，即． 2分 ‎（2）解：如图3，作，，‎ 垂足分别为，则．‎ 图3‎ 在中，，．…………1分 又，且，‎ ‎，得．……………………1分 同理可知，在中，．……………1分 ‎，．‎ 又，，．‎ ‎，． 1分 ‎，，四边形是平行四边形，． 1分 ‎． 1分 ‎24．（1）解：函数，是常数）图象经过，． 1分 设交于点，据题意，可得点的坐标为，点的坐标为，‎ 点的坐标为， 1分 ‎，，．‎ 由的面积为4，即， 1分 得，点的坐标为． 1分 ‎（2）证明：据题意，点的坐标为，，‎ ‎，易得，，‎ ‎，． 2分 ‎． 1分 ‎． 1分 ‎（3）解：，当时，有两种情况：‎ ①当时，四边形是平行四边形，‎ 由（2）得，，，得．‎ 点的坐标是（2，2）． 1分 设直线的函数解析式为，把点的坐标代入，‎ 得解得 直线的函数解析式是． 1分 ②当与所在直线不平行时，四边形是等腰梯形，‎ 则，，点的坐标是（4，1）． 1分 设直线的函数解析式为，把点的坐标代入，‎ 得解得 直线的函数解析式是． 1分 综上所述，所求直线的函数解析式是或．‎ ‎25．（1）证明：如图4，连结，‎ 是等边三角形的外心，， 1分 圆心角．‎ 当不垂直于时，作，，垂足分别为．‎ 由，且，‎ ‎，．‎ ‎． 1分 ‎． 1分 ‎．点在的平分线上． 1分 当时，．‎ 即，点在的平分线上．‎ 综上所述，当点在射线上运动时，点在的平分线上．‎ 图4‎ 图5‎ ‎（2）解：如图5，‎ 平分，且，‎ ‎． 1分 由（1）知，，，‎ ‎，．‎ ‎，． 1分 ‎．‎ ‎．．． 1分 定义域为：． 1分 ‎（3）解：①如图6，当与圆相切时，； 2分 ‎②如图7，当与圆相切时，； 1分 ‎③如图8，当与圆相切时，． 2分 图6‎ 图7‎ 图8‎