北京中考专题圆

北京中考专题圆

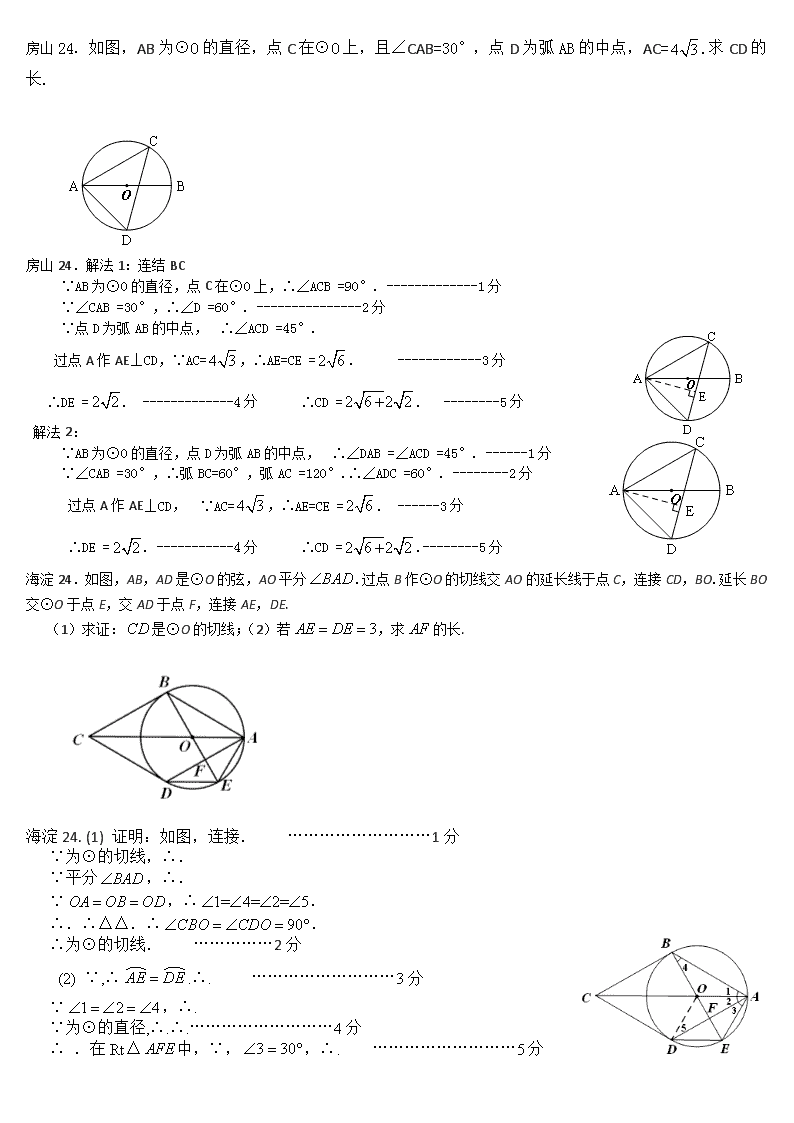
‎2016年北京模拟专题---圆 朝阳24．（本小题5分）‎ 如图，以△ABC的一边BC为直径的⊙O，交AB于点D，连接CD，OD，‎ 已知∠A+∠1=90°．‎ ‎（1）求证：AC是⊙O的切线；（2）若∠B=30°，AD=2，求⊙O的半径． ‎ 朝阳24.（1）证明：依题意，得 ∠B=∠1． …………………………………1分 ‎∵∠A+∠1=90°，∴∠A+∠B=90°.∴∠ACB=90°.∴AC⊥BC.‎ ‎∵BC是⊙O的直径，∴AC是⊙O的切线． …… …………………………………2分 ‎ （2） 解：∵BC是⊙O的直径，∴∠CDB=∠ADC=90°． ……………………………………3分 ‎∵∠B=30°，∴∠A=60°，∠ACD=30°．∴AC=2AD=4． ………………………………4分 ‎∴． ∴⊙O的半径为． …………………5分 东城25. 如图，AB为⊙O的直径，PD切⊙O于点C，与BA的延长线交于点D，DE⊥PO交PO延长线于点E，连接PB，∠EDB=∠EPB．‎ （1） 求证：PB是⊙O的切线．（2）若PB=3，DB=4，求DE的长．‎ 东城25. 解：（1）证明：∵ ∠EDB=∠EPB，∠DOE=∠POB，‎ ‎∴ ∠E=∠PBO=90゜，‎ ‎∴ PB是⊙O的切线．…………2分 ‎（2）∵ PB=3，DB=4，∴ PD=5.‎ 设⊙O的半径的半径是r，连接OC.‎ ‎∵ PD切⊙O于点C，∴ OC⊥PD.‎ ‎∴ ‎ ‎∴ ∴‎ 可求出.易证△DEP∽△OBP.∴ .解得 . ……5分 ‎ 房山24．如图，AB为⊙O的直径，点C在⊙O上，且∠CAB=30°，点D为弧AB的中点，AC=.求CD的长. ‎ 房山24．解法1：连结BC ‎∵AB为⊙O的直径，点C在⊙O上，∴∠ACB =90°. -------------1分 ‎∵∠CAB =30°，∴∠D =60°. ---------------2分 ‎∵点D为弧AB的中点，∴∠ACD =45°. ‎ 过点A作AE⊥CD，∵AC=，∴AE=CE =. ------------3分 ‎∴DE =. -------------4分 ∴CD =. --------5分 解法2：‎ ‎∵AB为⊙O的直径，点D为弧AB的中点，∴∠DAB =∠ACD =45°. ------1分 ‎∵∠CAB =30°，∴弧BC=60°，弧AC =120°.∴∠ADC =60°. --------2分 过点A作AE⊥CD， ∵AC=，∴AE=CE =. ------3分 ‎∴DE =. -----------4分 ∴CD =.--------5分 海淀24．如图，AB，AD是⊙O的弦，AO平分.过点B作⊙O的切线交AO的延长线于点C，连接CD，BO.延长BO交⊙O于点E，交AD于点F，连接AE，DE.‎ ‎（1）求证：是⊙O的切线；（2）若，求的长.‎ 海淀24. (1) 证明：如图，连接． ………………………1分 ‎∵为⊙的切线，∴．‎ ‎∵平分，∴．‎ ‎∵，∴．‎ ‎∴．∴△△．∴．‎ ‎∴为⊙的切线． ……………2分 ‎ (2) ∵,∴.∴. ………………………3分 ‎∵，∴.‎ ‎∵为⊙的直径,∴.∴.………………………4分 ‎∴ ．在Rt△中，∵，，∴. ………………………5分 怀柔24.如图，在⊙O中，AB为直径，，弦CF与OB交于点E，过点F，A分别作⊙O的切线交于点H，且HF与AB的延长线交于点D．‎ （1） 求证：DF=DE;（2）若tan∠OCE＝，⊙O的半径为4，求AH的长．‎ 怀柔24. (1)证明：连结OF，如图.∴OF⊥DH.‎ ‎∵DH为⊙O的切线，OF为半径，∴∠OFD=90°。，即∠2+∠OFC=90°。‎ ‎∵OC=OF，∴∠C=∠OFC，∴.‎ 而，∴.∴. ‎ ‎∵，∴.∴DE=DF ……………………………2分 ‎(2)解：∵tan∠OCE＝，⊙的半径为4，∴OE=2.‎ ‎∵DE=DF.在Rt△ODF中，OF=4,设，则DF=x，OD=2+x.‎ ‎∵OF2+FD2=OD2，∴x2+42=(2+x)2，解得x=3.∴DF=3，OD=5.‎ ‎∵AH为⊙的切线，为半径，DH为⊙的切线，∴AD⊥AH，HA=HF.∴∠HAD=90°.-------------------4分 在Rt△DAH中，设FH=t，则DH=t+3.∵AH2+AD2=HD2.∴t2+92=(t+3)2，解得t=12.∴AH=12. ---------------5分 门头沟24．如图，AB为⊙O的直径，⊙O过AC的中点D，DE为⊙O的切线．‎ ‎（1）求证：DE⊥BC；（2）如果DE=2，tanC=，求⊙O的直径．‎ 门头沟24．（本小题满分5分）‎ ‎（1）证明：连接OD． ∵DE为⊙O的切线， ∴DE⊥OD，……………………………………1分 ‎∵AO=OB，D是AC的中点，∴OD∥BC．∴DE⊥BC．……………………………………2分 ‎（2）解：连接DB，‎ ‎∵AB为⊙O的直径，∴∠ADB=90°，‎ ‎∴DB⊥AC，∴∠CDB=90°．∵D为AC中点，∴AB=BC，‎ 在Rt△DEC中，∠DEC=90°，∵DE=2，tanC=， ‎ ‎∴，……………………3分 由勾股定理得：DC=，在Rt△DCB中，∠BDC=90°，∴BD=DC·tanC＝，…………………………4分 由勾股定理得：BC=5，∴AB=BC=5， ∴⊙O的直径为5．…………………………………………5分 平谷24．如图，AB是⊙O的直径，AE是弦，C是劣弧AE的中点，过C作CD⊥AB于D，过C作CG∥AE交BA的延长线于点G．‎ ‎（1）求证：CG是⊙O的切线；（2）若∠EAB=30°，CF=2，求AG的长．‎ 平谷24．（1）证明：连接OC.‎ ‎∵AE是弦，C是劣弧AE的中点，∴OC⊥AE.…………………1‎ ‎∵CG∥AE，∴OC⊥GC.∴CG是⊙O的切线. …………………………2‎ ‎（2）解：连接AC.‎ ‎∵∠EAB=30°，CG∥AE,∴∠G=∠EAB=30°.‎ ‎∵CG是⊙O的切线，∴∠GCO=90°.∴∠COA=60°.‎ ‎∵OA=OC,∴△AOC是等边三角形.∴∠CAO=60°.∴∠CAF=30°.‎ 可求∠ACD=30°.‎ ‎ ∴ AF=CF=2.…………………3‎ ‎∵∠EAB=30°，∴DF=1，，‎ ‎∵CG∥AE，∴．…………………4‎ ‎∴. ∴.………………………………………………………………………5‎ 石景山25．如图，在△ABC中，AB=AC，以AC为直径作⊙O交BC于点D，过点D作⊙O的切线，交AB于点E，交CA的延长线于点F．‎ ‎（1）求证：EF⊥AB；（2）若∠C=30°，，求EB的长．‎ 石景山25．（1）证明：连接OD，AD，‎ ‎∵AC为⊙O的直径，∴∠ADC=90°． ‎ 又∵AB=AC，∴CD=DB．又CO=AO， ‎ ‎∴OD∥AB． ……………………1分 ‎∵FD是⊙O的切线，∴OD⊥DF． ∴FE⊥AB．………2分 ‎（2）解：∵，∴‎ 在Rt△中，， ‎ ‎∴． ∴‎ 在Rt△中，，‎ ‎∵，∴． …………………………………………3分 ‎∵，∴．………………………4分 ‎∴． …………………………………………………………5分 顺义25．如图，D为⊙O上一点，点C在直径BA的延长线上，且∠CDA=∠CBD．‎ （1） 求证：CD是⊙O的切线；‎ ‎（2）过点B作⊙O的切线交CD的延长线于点E，若BC=6，，求BE的长．‎ 顺义25．（1）证明：连接OD,OE ‎∵AB为直径，∴∠ADB=90°，即∠ADO+∠1=90°，又∵∠CDA=∠CBD，而∠CBD=∠ODB,‎ ‎∴∠ODB=∠CDA，∴∠CDA+∠ADO=90°，即∠CDO=90°，∴CD是○O的切线；‎ ‎（2）∵EB为○O的切线，∴ED=EB,OE⊥DB,∴∠ABD+∠DBE=90°，∠OEB+∠DBE=90°，∴∠CDA=∠OEB．‎ 而tan∠CDA=,∴tan∠OEB==,∵Rt△CDO∽Rt△CBE,∴∴CD=,‎ 在Rt△CBE中，设BE=x∴，解得即BE的长为 通州26．如图，已知AB是⊙O的直径，点P在BA的延长线上，PD切⊙O于点D，过点B作BE⊥PD，交PD的延长线于点C，连接AD并延长，交BE于点E．‎ ‎（1）求证：AB=BE；‎ ‎（2）连结OC，如果PD=，∠ABC=，求OC的长．‎ 通州26（1）证明：连结OD.‎ ‎∵OA=OD，∴， ∵PD切⊙O于点D，∴PD⊥OD，‎ ‎∵BE⊥PD，∴OD∥BE，… 1分；‎ ‎∴，∴，∴AB=BE.‎ ‎（2）解：∵OD∥BE，∠ABC=， ∴，‎ ‎∵ PD⊥OD， ∴，∴，∴，…… 3分；‎ ‎∴，∴，∴，∴，∴，‎ ‎∴，……4分；∴，∴，∴（舍负）.…5分；‎ 西城24．如图，在中，是的直径，与交于点．点在上，连接，，连接并延长交于点，．‎ ‎（1）求证：；‎ ‎（2）若，，，求的长．‎ 西城 延庆25. 已知：如图，AB为⊙O的直径，PA、PC是⊙O的切线，A、C为切点，∠BAC=30．‎ （1） 求∠P的大小；（2）若AB=6，求PA的长． ‎ 延庆25. （1）解：∵PA是⊙O的切线，AB为⊙O的直径，∴ ．‎ ‎∴．…………………………………1分 ‎ ∵ ∠BAC=30， ∴ ．‎ ‎ 又∵PA、PC切⊙O于点A、C，∴ ．…………………………………2分 ‎∴△PAC是等边三角形．∴ ．…………………………………3分 ‎( 2 ) 如图，连结BC．∵AB是直径，∠ACB=90．…………………………………4分 ‎ 在Rt△ACB中，AB=6，∠BAC=30，∴．‎ 又∵△PAC是等边三角形，∴ ． …………………………………5分 燕山24．如图，AB为⊙O的直径，C，D为⊙O上不同于A，B的两点，过点C作⊙O的切线CF交直线AB于点F，直线DB⊥CF于点E．‎ ‎(1) 求证：∠ABD＝2∠CAB；‎ ‎(2) 若BF＝5，sin∠F＝，求BD的长．‎ 燕山24．（1）证明：如图，连接OC，‎ ‎∵OA＝OC，∴∠CAB＝∠1∴∠2＝∠CAB＋∠1＝2∠CAB．‎ ‎∵CF切⊙O于C，OC是⊙O的半径，∴OC⊥CF． ‎ ‎∵DB⊥CF，∴OC∥DB，∴∠ABD＝∠2，∴∠ABD＝2∠CAB． ‎ ‎(2) 如图，连接AD，∵AB为⊙O的直径，∴∠ADB＝90°，即AD⊥DE．‎ ‎∵DE⊥CF，∴AD∥CF，∴∠3＝∠F． ……………………3分 在Rt△BEF中，∵∠BEF＝90°，BF＝5，sin∠F＝，∴BE＝BF•sin∠F＝5×＝3．‎ ‎∵OC∥BE， ∴△FBE∽△FOC，∴＝，‎ 设⊙O的半径为，则＝，解得 ＝． …………………4分 在Rt△ABD中，∠ADB＝90°，AB＝2＝15，sin∠3＝sin∠F＝，∴BD＝AB•sin∠3＝15×＝9． ‎ 朝阳2.24．如图，O是∠MAN的边AN上一点，以OA为半径作⊙O，交∠MAN的平分线于点D，DE⊥AM于E．‎ ‎ （1）求证：DE是⊙O的切线；‎ ‎ （2）连接OE，若∠EDA=30º，AE=1，求OE的长．‎ 朝阳2.24．（1）证明：连接．‎ ‎ ∵平分， ∴．‎ ‎ ∵， ∴． ∴．‎ ‎ ∵于， ∴．‎ ‎ ∴， ‎ ‎ ∴．‎ ‎∴． ∴是⊙的切线． ………………2分 ‎ （2）解：∵，∴．‎ ‎∵，∴△为等边三角形．………………………3分 在△中，，可得，．………………4分 ‎∴．在△中，由勾股定理可得．…5分 昌平2.‎ 昌平2‎ 房山2.26.如图，△ABC 中，AB=AC，以AB为直径的⊙O与BC相交于点D，与CA的延长线相交于点E，DF过点D作⊙O的切线交AC于点F．‎ （1） 求证：DF⊥AC；如果，AE的长为2.求⊙O的半径．‎ 房山2.26.（1）证明：连接OD ． ‎ ‎∵DF是⊙O的切线，∴ OD⊥DF．------------1分 ‎∵ OB=OD，∴ ∠B=∠ODB．‎ ‎∵AB=AC．∴ ∠B=∠C．∴ ∠ODB=∠C ‎ ∴ OD∥AC．------2分∴DF⊥AC，----3分 ‎（2）解：连结BE，AD ． ‎ ‎∵ AB是直径，∴ ∠ADB=∠AEB=90°∵ AB=AC，∴BD=CD．∵ DF⊥AC ∴FD∥BE ‎∴可得点F是CE的中点.∴sin∠ABD= sin∠ACB= sin∠ADF=‎ 设⊙O的半径为r,则AB=2r,AC=2r ‎∴AD=,AF=r-1‎ ‎∵sin∠ADF== ∴r=3 ---------5分∴⊙O的半径为3.‎ 丰台2.24. 如图，AB是⊙O的直径，BD交⊙O于点C，E为 的中点，连接AE交BD于点F，作，垂足为G，连接AD，且． ‎ （1） 求证：AD为⊙O的切线；（2）若cosD =，AD = 6，求FG的长．‎ 丰台2.24.证明：连接.‎ ‎ ∵是的直径 ∴. ∴. ‎ ‎ ∵E为的中点,∴. ∴. ‎ ‎ ∵, ∴. ------- 1分 ‎ ∴. ∴.即.‎ ‎ 又∵是直径, ∴是的切线. ------- 2分 ‎（2）∵在Rt△中,‎ ‎，, ------- 3分 ‎∵在Rt△中,，,∴.‎ ‎∵,,，∴. ------- 4分 设.∵，∴.∴.∴.‎ ‎∵.∴.解得.∴. ------- 5分 东城2.‎ 东城2‎ 海淀2.24．如图，在△ABC中，∠C=90°，点E在AB上，以AE为直径的⊙O切BC于点D，连接AD．‎ ‎（1）求证：AD平分∠BAC；（2）若⊙O的半径为5，sin∠DAC=，求BD的长. ‎ 海淀2.24. （1）证明：连接．………………………1分 ‎∵⊙O切BC于点D， ，∴．‎ ‎∴∥．∴．‎ ‎∵，∴．‎ ‎∴．∴平分．………………………2分 ‎（2）解：连接．‎ ‎∵AE为直径，∴．‎ ‎∵，sin，∴sin ．‎ ‎∵，∴． ∴．∴，．‎ ‎∵∥，∴．………………………4分 ‎∴．即．∴．………………………5分 石景山2.25．如图，在Rt△ACB中，∠C=90°，D是AB上一点，以BD为直径的⊙O切AC于点E，交BC于点F，连接DF．‎ （1） 求证：DF=2CE；（2）若BC=3，sinB=，求线段BF的长．‎ 石景山2.25．（1）证明：连接OE交DF于G，‎ ‎ ∵AC切⊙O于E，∴∠CEO=90°．又∵BD为⊙O的直径，∴∠DFC=∠DFB=90°．‎ ‎∵∠C=90°，∴四边形CEGF为矩形．∴CE=GF，∠EGF=90°…………1分 ‎∴DF=2CE．………………………………2分 ‎（2）解：在Rt△ABC中，∠C=90°，‎ ‎∵BC=3，，∴AB=5．…………………………………3分 设OE=x，∵OE//BC，∴△AOE∽△ABC．‎ ‎∴，∴，∴．………4分 ∴BD=．‎ 在Rt△BDF中，∠DFB=90°，∴BF=…………………………5分 顺义2.24．已知：如图，在中，以为直径的⊙分别交、于点、，且.‎ ‎（1）求证：；（2）过点作⊙的切线，交的延长线于点，且，求的值.‎ 顺义2.24．（1）证明：∵为⊙的直径，∴.………………..……1分 又∵，∴.…………2分 ‎（2）解：∵BF切⊙于点B，∴.………..…………3分 ‎∴.‎ 又∵，∴，∴△∽△，∴，∴.‎ 又∵，∴，‎ 设，则，‎ ‎∴.在RT△中，，,‎ 又∵，…….……4分∴.………………5分 通州2.26. 如图：ΔABC是⊙O的内接三角形，∠ACB=45°，∠AOC=150°，过点C作⊙O的切线交AB的延长线于点D.‎ （1） 求证：CD=CB；（2）如果⊙O的半径为，求AC的长.‎ 通州2.‎ 西城2.24．如图，四边形ABCD 内接于⊙O，点E 在CB 的延长线上，连接AC，AE，∠ACD=∠BAE=45°‎ ‎（1）求证：AE 是⊙O 的切线；（2）若 AB=AD，AC= 2，tan∠ADC＝3，求 CD的长．‎ 西城2.‎