中考数学一轮复习74实验操作型问题试卷部分

中考数学一轮复习74实验操作型问题试卷部分

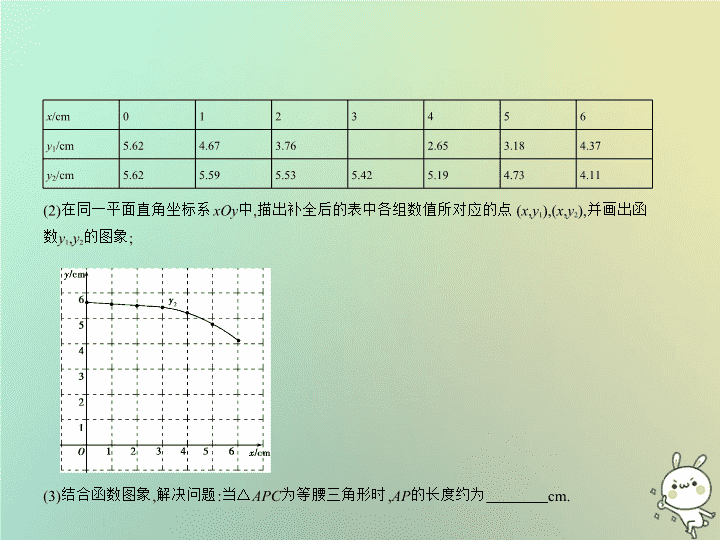
§7.4 　实验操作型问题 中考数学 ( 北京专用 ) 1. (2018北京,24,6分)如图, Q 是   与弦 AB 所围成的图形的内部的一定点, P 是弦 AB 上一动点,连 接 PQ 并延长交   于点 C ,连接 AC .已知 AB =6 cm,设 A , P 两点间的距离为 x cm, P , C 两点间的距离 为 y 1 cm, A , C 两点间的距离为 y 2 cm.   小腾根据学习函数的经验,分别对函数 y 1 , y 2 随自变量 x 的变化而变化的规律进行了探究. 下面是小腾的探究过程,请补充完整: (1)按照下表中自变量 x 的值进行取点、画图、测量,分别得到了 y 1 , y 2 与 x 的几组对应值; 好题精练 x /cm 0 1 2 3 4 5 6 y 1 /cm 5.62 4.67 3.76 2.65 3.18 4.37 y 2 /cm 5.62 5.59 5.53 5.42 5.19 4.73 4.11 (2)在同一平面直角坐标系 xOy 中,描出补全后的表中各组数值所对应的点( x , y 1 ),( x , y 2 ),并画出函 数 y 1 , y 2 的图象;   (3)结合函数图象,解决问题:当△ APC 为等腰三角形时, AP 的长度约为 　　　     cm. 解析 　(1)通过画图观察可得当 x =3时, y 1 =3.00. (2)如图所示.   (3)3.00或4.83或5.86.在坐标系中画出直线 y = x ,则三个图象中,两两图象交点的横坐标即为 △ APC 为等腰三角形时线段 AP 的长度,则 AP 的长度约为3.00 cm 或4.83 cm或5.86 cm. 2. (2017北京,26,6分)如图, P 是   所对弦 AB 上一动点,过点 P 作 PM ⊥ AB 交   于点 M ,连接 MB ,过 点 P 作 PN ⊥ MB 于点 N .已知 AB =6 cm,设 A , P 两点间的距离为 x cm, P , N 两点间的距离为 y cm.(当 点 P 与点 A 或点 B 重合时, y 的值为0)   小东根据学习函数的经验,对函数 y 随自变量 x 的变化而变化的规律进行了探究. 下面是小东的探究过程,请补充完整: (1)通过取点、画图、测量,得到了 x 与 y 的几组值,如下表: x /cm 0 1 2 3 4 5 6 y /cm 0 2.0 2.3 2.1 0.9 0 (说明:补全表格时相关数值保留一位小数) (2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;   (3)结合画出的函数图象,解决问题:当△ PAN 为等腰三角形时, AP 的长度约为 　　　     cm. 解析 　(1) x /cm 0 1 2 3 4 5 6 y /cm 0 2.0 2.3 2.1 1.6 0.9 0 (2)   (3)2.25.(答案不唯一) 提示:当△ PAN 为等腰三角形时,只有 AP = PN 这一种可能,则有 y = x ,求函数 y = x 的图象与所画出 的函数图象的交点即可. 3. (2014北京,22,5分)阅读下面材料: 小腾遇到这样一个问题:如图1,在△ ABC 中,点 D 在线段 BC 上,∠ BAD =75 ° ,∠ CAD =30 ° , AD =2, BD =2 DC ,求 AC 的长.   小腾发现,过点 C 作 CE ∥ AB ,交 AD 的延长线于点 E ,通过构造△ ACE ,经过推理和计算能够使问 题得到解决(如图2) . 请回答:∠ ACE 的度数为 　　　     , AC 的长为 　　　     . 参考小腾思考问题的方法,解决问题: 如图 3, 在四边形 ABCD 中 ,∠ BAC =90 ° ,∠ CAD =30 ° ,∠ ADC =75 ° , AC 与 BD 交于点 E , AE =2, BE =2 ED , 求 BC 的长 .   图 3 解析 　∠ ACE 的度数为75 ° , AC 的长为3. 解决问题: 过点 D 作 DF ∥ AB 交 AC 于点 F ,如图.   ∴∠ DFE =∠ BAC =90 ° , 又∠ AEB =∠ FED , ∴△ ABE ∽△ FDE . ∴   =   =   . ∵ BE =2 ED , AE =2,∴ FE =1,∴ AF =3. ∵∠ CAD =30 ° ,∴ FD =   , AD =2   . ∵   =2,∴ AB =2   . ∵∠ ADC =75 ° ,∠ CAD =30 ° ,∴∠ ACD =75 ° , ∴ AC = AD =2   . 在Rt△ ABC 中,由勾股定理可得 BC =2   . 思路分析     由平行线的性质及三角形内角和定理求得∠ ACE =75 ° ,利用相似求得 DE 的长,即可 得 AE 的长,再利用等腰三角形的性质求得 AC 的长.(2)作 DF ∥ AB ,通过相似得到   的值,再通 过勾股定理计算 BC 的长. 解题关键     由 BE =2 ED ,可知 BE 与 DE 的比值,由条件与材料发现,解决此题的关键是构建相似 三角形. 4. (2013北京,22,5分)阅读下面材料: 小明遇到这样一个问题:如图1,在边长为 a ( a >2)的正方形 ABCD 各边上分别截取 AE = BF = CG = DH =1,当∠ AFQ =∠ BGM =∠ CHN =∠ DEP =45 ° 时,求正方形 MNPQ 的面积.   　　　       图1　　　　　　　　　　　　图2 小明发现,分别延长 QE , MF , NG , PH 交 FA , GB , HC , ED 的延长线于点 R , S , T , W ,可得△ RQF ,△ SMG , △ TNH ,△ WPE 是四个全等的等腰直角三角形(如图2). 请回答: (1)若将上述四个等腰直角三角形拼成一个新的正方形(无缝隙不重叠),则这个新正方形的边 长为 　　　     ; (2)求正方形 MNPQ 的面积. 参考小明思考问题的方法,解决问题: 如图3,在等边△ ABC 各边上分别截取 AD = BE = CF ,再分别过点 D , E , F 作 BC , AC , AB 的垂线,得到 等边△ RPQ ,若 S △ RPQ =   ,则 AD 的长为 　　　     .   图3 解析 　 (1) a . (2) 由 (1) 可知 , 由△ RQF ,△ SMG ,△ TNH ,△ WPE 拼成的新正方形的面积与正方形 ABCD 的面积 相等 . ∴△ RAE ,△ SBF ,△ TCG ,△ WDH 这四个全等的等腰直角三角形的面积之和等于正方形 MNPQ 的面积 . ∵ AE = BF = CG = DH =1, ∴ 正方形 MNPQ 的面积 S =4 ×   × 1 × 1=2. 解决问题 : AD =   . 5. (2018北京东城一模,25)如图,在等腰△ ABC 中, AB = AC ,点 D , E 分别为 BC , AB 的中点,连接 AD .在 线段 AD 上任取一点 P ,连接 PB , PE .若 BC =4, AD =6,设 PD = x (当点 P 与点 D 重合时, x 的值为0), PB + PE = y .小明根据学习函数的经验,对函数 y 随自变量 x 的变化而变化的规律进行了探究.   下面是小明的探究过程,请补充完整: (1)通过取点、画图、计算,得到了 x 与 y 的几组值,如下表: x 0 1 2 3 4 5 6 y 5.2 4.2 4.6 5.9 7.6 9.5 (说明:补全表格时,相关数值保留一位小数,参考数据:   ≈ 1.414,   ≈ 1.732,   ≈ 2.236) (2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;   (3)函数 y 的最小值为 　　　     (保留一位小数),此时点 P 的位置为 　　　     . 解析 　(1)4.5. (2)如图.   (3)4.2; AD 与 CE 的交点. 思路分析     解决类比探究题需要精准画图和简单的逻辑推理(有的题目是不能准确求出表达 式的,即使求出来了,也不是学习过的,也不好用函数知识解决). 6. (2018北京西城一模,25)如图, P 为☉ O 的直径 AB 上的一个动点,点 C 在   上,连接 AC , PC ,过点 A 作 PC 的垂线交☉ O 于点 Q .已知 AB =5 cm, AC =3 cm,设 A , P 两点间的距离为 x cm, A , Q 两点间的距 离为 y cm.   某同学根据学习函数的经验,对函数 y 随自变量 x 的变化而变化的规律进行了探究. 下面是该同学的探究过程,请补充完整: (1)通过取点、画图、测量及分析,得到了 x 与 y 的几组值,如下表: x (cm) 0 1 2.5 3 3.5 4 5 y (cm) 4.0 4.7 5.0 4.8 4.1 3.7 (说明:补全表格时,相关数值保留一位小数) (2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;   (3)结合画出的函数图象解决问题:当 AQ =2 AP 时, AP 的长度约为 　　　     cm. 解析 　(1) x (cm) 0 1 1.8 2.5 3 3.5 4 5 y (cm) 4.0 4.7 5.0 4.8 4.5 4.1 3.7 3.0 (2)如图.   (3)2.42. 提示:借助上一问的图,当 x =2.5时, y =4.8, AQ <2 AP ,而当 x =1.8时, y =5, AQ >2 AP ,所以 x <2.5,且接近 2.5. 7. (2018北京海淀一模,25)在研究反比例函数 y =   的图象与性质时,我们对函数解析式进行了深 入分析.首先,确定自变量 x 的取值范围是全体非零实数,因此函数图象会被 y 轴分成两部分;其 次,分析解析式,得到 y 随 x 的变化趋势:当 x >0时,随着 x 值的增大, y 的值减小,且逐渐接近于零,随 着 x 值的减小, y 的值会越来越大,由此,可以大致画出 y =   在 x >0时的部分图象,如图1所示.   图1 利用同样的方法,我们可以研究函数 y =   的图象与性质.通过分析解析式画出部分函数图 象,如图2所示.   图2 (1)请沿此思路在图2中完善函数图象的草图并标出此函数图象上横坐标为0的点 A ;(画出网格 区域内的部分即可) (2)观察图象,写出该函数的一条性质: 　　　　　　　     ; (3)若关于 x 的方程   = a ( x -1)有两个不相等的实数根,结合图象,直接写出实数 a 的取值范围: 　　　　　     . 解析 　(1)如图.   (2)当 x >1时, y 随着 x 的增大而减小(答案不唯一). (3) a ≥ 1. 提示:有两个不相等的实根即函数 y =   与 y = a ( x -1)的图象有两个交点,借助图象解得 a ≥ 1. 解题关键     解决本题的关键是要准确画出图象,并借助函数与方程的关系来解决. 8. (2018北京朝阳一模,25)如图, AB 是☉ O 的直径, AB =4 cm, C 为 AB 上一动点,过点 C 的直线交☉ O 于 D 、 E 两点,且∠ ACD =60 ° , DF ⊥ AB 于点 F , EG ⊥ AB 于点 G ,当点 C 在 AB 上运动时,设 AF = x cm, DE = y cm(当 x 的值为0或3时, y 的值为2),某同学根据学习函数的经验,对函数 y 随自变量 x 的变化 而变化的规律进行了探究.   下面是该同学的探究过程,请补充完整: (1)通过取点、画图、测量,得到了 x 与 y 的几组对应值,如下表: x /cm 0 0.40 0.55 1 1.80 2.29 2.61 3 y /cm 2 3.68 3.84 3.65 3.13 2.70 2 (2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;   (3)结合画出的函数图象解决问题:点 F 与点 O 重合时, DE 的长度约为 　　　     cm(结果保留一 位小数). 解析 　(1) (2)如图.   (3)3.5. 提示:此时△ DOE 是腰长为2,顶角为120 ° 的等腰三角形,所以 DE 的长度为2   ≈ 3.5 cm. x /cm 0 0.40 0.55 1.00 1.80 2.29 2.61 3 y /cm 2 3.68 3.84 4 3.65 3.13 2.70 2 9. (2018北京丰台一模,25)如图,Rt△ ABC 中,∠ ACB =90 ° ,点 D 为 AB 边上的动点(点 D 不与点 A ,点 B 重合),过点 D 作 ED ⊥ CD 交直线 AC 于点 E .已知∠ A =30 ° , AB =4 cm,在点 D 由点 A 到点 B 运动的过 程中,设 AD = x cm, AE = y cm.   小东根据学习函数的经验,对函数 y 随自变量 x 的变化而变化的规律进行了探究. 下面是小东的探究过程,请补充完整: (1)通过取点、画图、测量,得到了 x 与 y 的几组值,如下表: x /cm 0.5 1 1.5 2 2.5 3 3.5 y /cm 0.4 0.8 1.0 1.0 0 4.0 (说明:补全表格时,相关数值保留一位小数) (2)在下面的平面直角坐标系 xOy 中描出以补全后的表中各对对应值为坐标的点,画出该函数 的图象;   (3)结合画出的函数图象解决问题:当 AE =   AD 时, AD 的长度约为 　　　     cm. 解析 　(1)1.2. (2)如图.   (3)2.4或3.3. 提示:在(2)的图中画出 y =   x 的图象,两图象交点的横坐标即为所求. 10. (2018北京石景山一模,25)如图,半圆 O 的直径 AB =5 cm,点 M 在 AB 上且 AM =1 cm,点 P 是半圆 O 上的动点,过点 B 作 BQ ⊥ PM ,交 PM (或 PM 的延长线)于点 Q .设 PM = x cm, BQ = y cm.(当点 P 与点 A 或点 B 重合时, y 的值为0)   小石根据学习函数的经验,对函数 y 随自变量 x 的变化而变化的规律进行了探究. 下面是小石的探究过程,请补充完整: (1)通过取点、画图、测量,得到了 x 与 y 的几组值,如下表: x /cm 1 1.5 2 2.5 3 3.5 4 y /cm 0 3.7 3.8 3.3 2.5 (2) 建立平面直角坐标系 , 描出以补全后的表中各对对应值为坐标的点 , 画出该函数的图象 ;   (3) 结合画出的函数图象解决问题 : 当 BQ 与直径 AB 所夹的锐角为 60 ° 时 , PM 的长度约为 　　          cm. 解析 　(1)4;0. (2)如图.   (3)1.1或3.7. 提示:在(2)的图中作直线 y =2,该直线与函数图象交点的横坐标即为所求. 11. (2018北京顺义一模,25)如图, P 是半圆上一动点, AB 为直径,连接 PA 、 PB ,过圆心 O 作 OC ∥ BP 交 PA 于点 C ,连接 CB .已知 AB =6 cm,设 O , C 两点间的距离为 x cm, B , C 两点间的距离为 y cm.   小东根据学习函数的经验,对函数 y 随自变量 x 的变化而变化的规律进行探究. 下面是小东的探究过程,请补充完整: (1)通过取点、画图、测量,得到了 x 与 y 的几组值,如下表: x /cm 0 0.5 1 1.5 2 2.5 3 y /cm 3 3.1 3.5 4.0 5.3 6 (说明:补全表格时,相关数据保留一位小数) (2)建立直角坐标系,描出以补全后的表中各组对应值为坐标的点,画出该函数的图象;   (3)结合画出的函数图象解决问题:直接写出△ OBC 的周长 C 的取值范围: 　　　　     . 解析 　(1)4.6. (2)如图.   (3)6< C <12. 提示:△ OBC 的周长为 x + y +3. 12. (2018北京西城二模,25)阅读下面材料: 已知:如图,在正方形 ABCD 中,边 AB = a 1 .   按照以下操作步骤,可以从该正方形开始,构造一系列的正方形,它们之间的边满足一定的关 系,并且一个比一个小. 操作步骤 作法 由操作步骤推断 ( 仅选取部分结论 ) 第一步 在第一个正方形 ABCD 的对角线 AC 上截取 AE = a 1 , 再作 EF ⊥ AC 于点 E , EF 与边 BC 交于点 F , 记 CE = a 2 (1)△ EAF ≌△ BAF ( 判断依据是 　①     ); (2)△ CEF 是等腰直角三角形 ; (3) 用含 a 1 的式子表示 a 2 为 　②     第二步 以 CE 为边构造第二个正方形 CEFG 第三步 在第二个正方形的对角线 CF 上截取 FH = a 2 , 再 作 IH ⊥ CF 于点 H , IH 与边 CE 交于点 I , 记 IH = a 3 (4) 用含 a 1 的式子表示 a 3 为 　③     第四步 以 IH 为边构造第三个正方形 CHIJ 这个过程可以不断进行下去 . 若第 n 个正方形的边长为 a n , 用只含 a 1 的式子表示 a n 为 　④     请解决以下问题: (1)完成表格中的填空: ① 　　　　     ;② 　　　　     ; ③ 　　　　     ;④ 　　　　     . (2)根据以上第三步、第四步的作法画出第三个正方形 CHIJ (不要求尺规作图). 解析 　 (1)① 斜边和一条直角边分别相等的两个直角三角形全等 . ②(   -1) a 1 . ③(   -1) 2 a 1 . ④(   -1) n -1 a 1 . (2) 所画正方形 CHIJ 如图 .   13. (2018北京丰台期末,25)如图,点 E 是矩形 ABCD 的边 AB 上一动点(不与点 B 重合),过点 E 作 EF ⊥ DE 交直线 BC 于点 F ,连接 DF .已知 AB =4 cm, AD =2 cm,设 A , E 两点间的距离为 x cm,△ DEF 的面 积为 y cm 2 . 小明根据学习函数的经验对函数 y 随自变量 x 的变化而变化的规律进行了探究.   下面是小明的探究过程,请补充完整: (1)自变量 x 的取值范围是 　　　     ; (2)通过取点、画图、测量,得到了 x 与 y 的几组值,如下表: x /cm 0 0.5 1 1.5 2 2.5 3 3.5 y /cm 4.0 3.7 3.9 3.8 3.3 2.0 (说明:补全表格时相关数值保留一位小数) (3)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;   (4)结合画出的函数图象解决问题:当△ DEF 的面积最大时, AE 的长度为 　　　     cm. 解析 　(1)0 ≤ x <4. (2)3.8;4.0. 提示:当 x =1时,根据三角形的面积公式,相似三角形的判定与性质,可知 S △ ADE =1, S △ EFB =2.25, S △ CDF =1,则 S △ DEF =8-1-2.25-1=3.75 ≈ 3.8.当 x =2时,点 F 恰与点 C 重合, S △ DEF =4.0. (3)如图.   (4)0或2. 14. (2017北京石景山二模,26)已知 y 是 x 的函数,下表是 y 与 x 的几组对应值. x … -5 -4 -3 -2 0 1 2 3 4 5 … y … 1.969 1.938 1.875 1.75 1 0 -2 -1.5 0 2.5 … 小明根据学习函数的经验,利用上述表格所反映出的 y 与 x 之间的变化规律对该函数的图象与 性质进行了探究. 下面是小明的探究过程,请补充完整: (1)如图,在平面直角坐标系 xOy 中,描出了以上表中各对对应值为坐标的点,根据描出的点画出 该函数的图象;   (2)根据画出的函数图象回答下列问题: ① x =-1对应的函数值 y 约为 　　　     ; ② 写出该函数的一条性质 : 　　　　　　　     . 解析 　本题答案不唯一 . 画出的函数图象需符合表格中所反映出的 y 与 x 之间的变化规律 , 写出 的函数值和函数性质需符合所画出的函数图象 . 如 : (1) 如图 .   (2)①1.5( 在 1.4 到 1.6 之间均可 ). ② 当 x <2 时 , y 随 x 的增大而减小 ; 当 x ≥ 2 时 , y 随 x 的增大而增大 ; 当 x =2时, y 有最小值-2; …… 写出一条即可. 15. (2017北京顺义二模,26)实验数据显示,一般成人喝250毫升低浓度白酒后,其血液中的酒精 含量(毫克/百毫升)随时间的增加逐渐增高,达到峰值后,随时间的增加逐渐降低. 小明根据相关数据和学习函数的经验对血液中酒精含量随时间变化的规律进行了探究,发现 血液中酒精含量 y 是时间 x 的函数,其中 y 表示血液中酒精含量(毫克/百毫升), x 表示饮酒后的时 间(小时). 下表记录了6小时内11个时间点血液中酒精含量 y (毫克/百毫升)随饮酒后的时间 x (小时)( x >0) 的变化情况: 饮酒后 的时间 x ( 小时 ) …       1     2 3 4 5 6 … 血液中 酒精含 量 y ( 毫 克 / 百 毫升 ) …   150   200   150   75   45   … 下面是小明的探究过程,请补充完整: (1)如图,在平面直角坐标系 xOy 中,描出了以上表中各对对应值为坐标的点,根据描出的点画出 血液中酒精含量 y 随时间 x 变化的函数图象;   (2)观察表中数据及图象可发现此函数图象在直线 x =   的两侧可以用不同的函数表达式表示, 请你任选其中一部分写出表达式; (3)按国家规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾 驶”,不能驾车上路.假设某驾驶员20:00在家喝完250毫升低浓度白酒,第二天6:30能否驾车去 上班?请说明理由. 解析 　 (1) 如图所示 .   (2) y =-200 x 2 +400 x   或 y =     . (3) 不能 . 理由 : 把 y =20 代入反比例函数 y =     得 x =11.25,20:00 经过 11.25 小时后为第二天 7:15, ∴ 第二天 7:15 以后才可以驾车 ,6:30 不能驾车去上班 . 16. (2017北京东城一模,26)在课外活动中,我们要研究一种凹四边形——燕尾四边形的性质. 定义1:把四边形的某些边向两方延长,其他各边有不在延长所得直线的同一旁,这样的四边形 叫做凹四边形(如图1).   (1)根据凹四边形的定义,下列四边形是凹四边形的是 　　     ;(填写序号)   ① 　　　　　　　　　②　　　　　　　　　③ 定义2:两组邻边分别相等的凹四边形叫做燕尾四边形(如图2). 特别地,有三条边相等的凹四边形不属于燕尾四边形. 小洁根据学习平行四边形、菱形、矩形、正方形的经验,对燕尾四边形的性质进行了探究. 下面是小洁的探究过程,请补充完整: (2)通过观察、测量、折叠等操作活动,写出两条对燕尾四边形性质的猜想,并选取其中的一条 猜想加以证明; (3)如图2,在燕尾四边形 ABCD 中, AB = AD =6, BC = DC =4,∠ BCD =120 ° ,求燕尾四边形 ABCD 的面 积(直接写出结果). 解析 　(1)②. (2)燕尾四边形是一个轴对称图形;两组邻边分别相等;一组对角相等;一条对角线所在的直线 垂直平分另一条对角线,等等. 已知:如图,在凹四边形 ABCD 中, AB = AD , BC = DC .   求证:∠ B =∠ D . 证明:连接 AC . ∵ AB = AD , CB = CD , AC = AC , ∴△ ABC ≌△ ADC . ∴∠ B =∠ D . (3)燕尾四边形 ABCD 的面积为12   -4   . 解题关键     解决第(3)问的关键是要借助120 ° 构造直角三角形,如图:   进而将题目转化为解直角三角形的问题. 17. (2016北京西城一模,26)有这样一个问题:如图,在四边形 ABCD 中, AB = AD , CB = CD ,我们把这 种两组邻边分别相等的四边形叫做筝形.请探究筝形的性质和判定方法.   小南根据学习四边形的经验,对筝形的性质和判定方法进行了探究. 下面是小南的探究过程: (1)由筝形的定义可知,筝形的边的性质是:筝形的两组邻边分别相等.关于筝形的角的性质,通 过测量、折纸的方法,猜想:筝形有一组对角相等. 请将下面证明此猜想的过程补充完整: 已知:在筝形 ABCD 中, AB = AD , CB = CD . 求证: 　　　　　　　　     . 证明: 　　　　　　　　     . 由以上证明可得,筝形的角的性质是:筝形有一组对角相等. (2)连接筝形的两条对角线,探究发现筝形的另一条性质:筝形的一条对角线平分另一条对角 线.结合图形,写出筝形的其他性质(一条即可):      . (3)筝形的定义是判定一个四边形为筝形的方法之一.试判断“一组对角相等,一条对角线平分 另一条对角线的四边形是筝形”是否成立.如果成立,请给出证明;如果不成立,请举出一个反 例,画出图形,并加以说明. 解析 　(1)已知:如图1,筝形 ABCD 中, AB = AD , CB = CD . 求证:∠ B =∠ D . 证明:连接 AC ,如图. 图1 在△ ABC 和△ ADC 中 ,   ∴△ ABC ≌△ ADC . ∴∠ B =∠ D . (2) 筝形的其他性质 : ① 筝形的两条对角线互相垂直 . ② 筝形的一条对角线平分一组对角 . ③ 筝形是轴对称图形 . …… ( 写出一条即可 ) (3) 不成立 . 反例如图 2 所示 .   图 2 在平行四边形 ABCD 中 , AB ≠ AD , 对角线 AC , BD 相交于点 O . 由平行四边形性质可知∠ ABC = ∠ ADC , AC 平分 BD , 但是该四边形不是筝形 .( 答案不唯一 ) 教师专用题组 1. (2017河北,16,2分)已知正方形 MNOK 和正六边形 ABCDEF 边长均为1,把正方形放在正六边 形中,使 OK 边与 AB 边重合,如图所示,按下列步骤操作: 将正方形在正六边形中绕点 B 顺时针旋转,使 KM 边与 BC 边重合,完成第一次旋转;再绕点 C 顺时 针旋转,使 MN 边与 CD 边重合,完成第二次旋转; …… 在这样连续6次旋转的过程中,点 B , M 间的 距离可能是   (　　)   A.1.4　    B.1.1　    C.0.8　    D.0.5 答案     C　在第一次旋转过程中, BM =1;在第二次旋转过程中,点 M 位置不变, BM =1;在第三次旋 转过程中, BM 的长由1逐渐变小为   -1;在第四次旋转过程中,点 M 在以点 E 为圆心,   为半径 的圆弧上, BM 的长由   -1逐渐变小为2-   ,然后逐渐变大为   -1;在第五次旋转过程中, BM 的 长由   -1逐渐变大为1;在第六次旋转过程中,点 M 位置不变, BM =1.显然连续6次旋转的过程中, 点 B , M 间的距离可能是0.8,故选C. 解题关键     解决本题的关键是求出每个旋转过程中 BM 长的变化范围. 2. (2016天津,18,3分)如图,在每个小正方形的边长为1的网格中, A , E 为格点, B , F 为小正方形边的 中点, C 为 AE , BF 的延长线的交点. (1) AE 的长等于 　　　     ; (2)若点 P 在线段 AC 上,点 Q 在线段 BC 上,且满足 AP = PQ = QB ,请在如图所示的网格中,用 无刻度 的直尺,画出线段 PQ ,并简要说明点 P , Q 的位置是如何找到的(不要求证明) 　　　　　　　     　　　     .   答案 　(1)   　(2)如图, AC 与网格线相交,得点 P ;取格点 M ,连接 AM 并延长与 BC 相交,得点 Q .连 接 PQ ,线段 PQ 即为所求   解题思路     (1)利用勾股定理求解;(2)构造全等三角形,列方程求解. 解题关键     关注 B 、 F 为中点,可知 BF = AE . 3. (2014天津,18,3分)如图,将△ ABC 放在每个小正方形的边长为1的网格中,点 A ,点 B ,点 C 均落在 格点上. (1)计算 AC 2 + BC 2 的值等于 　　　     ; (2)请在如图所示的网格中,用 无刻度 的直尺,画出一个以 AB 为一边的矩形,使该矩形的面积等 于 AC 2 + BC 2 ,并简要说明画图方法(不要求证明)                .   答案 　(1)11 (2)分别以 AC , BC , AB 为一边作正方形 ACED ,正方形 BCNM ,正方形 ABHF ;延长 DE 交 NM 于点 Q , 连接 QC ;平移 QC 至 AG , BP 位置;直线 GP 分别交 AF , BH 于点 T , S .则四边形 ABST 即为所求   解析 　(1)由题图可知, AC =   , BC =3,所以 AC 2 + BC 2 =(   ) 2 +3 2 =2+9=11. (2)四边形 BCNM 的面积=四边形 BCQJ 的面积=四边形 BCKP 的面积, 四边形 ACED 的面积=四边形 ACKG 的面积, 所以四边形 BCNM 的面积+四边形 ACED 的面积 =四边形 BCKP 的面积+四边形 ACKG 的面积 =五边形 AGKPB 的面积+△ ABC 的面积 =五边形 AGKPB 的面积+△ KGP 的面积 =四边形 AGPB 的面积 =四边形 ABST 的面积.   4. (2018河南,22,10分) (1)问题发现 如图1,在△ OAB 和△ OCD 中, OA = OB , OC = OD ,∠ AOB =∠ COD =40 ° ,连接 AC , BD 交于点 M .填空: ①   的值为 　　　     ; ②∠ AMB 的度数为 　　　     . (2)类比探究 如图2,在△ OAB 和△ OCD 中,∠ AOB =∠ COD =90 ° ,∠ OAB =∠ OCD =30 ° ,连接 AC 交 BD 的延长线 于点 M .请判断   的值及∠ AMB 的度数,并说明理由; (3)拓展延伸 在(2)的条件下,将△ OCD 绕点 O 在平面内旋转, AC , BD 所在直线交于点 M .若 OD =1, OB =   ,请直 接写出当点 C 与点 M 重合时 AC 的长.     解析 　(1)①1.   (1分) ②40 ° .(注:若填为40,不扣分)(2分) (2)   =   ,∠ AMB =90 ° .(注:若无判断,但后续证明正确,不扣分)(4分) 理由如下: ∵∠ AOB =∠ COD =90 ° ,∠ OAB =∠ OCD =30 ° ,∴   =   =   , 又∠ COD +∠ AOD =∠ AOB +∠ AOD ,即∠ AOC =∠ BOD . ∴△ AOC ∽△ BOD .   (6分) ∴   =   =   ,∠ CAO =∠ DBO . ∵∠ AOB =90 ° ,∴∠ DBO +∠ ABD +∠ BAO =90 ° . ∴∠ CAO +∠ ABD +∠ BAO =90 ° .∴∠ AMB =90 ° .   (8分) (3) AC 的长为2   或3   .   (10分) 【 提示 】 在△ OCD 旋转过程中 ,(2) 中的结论仍成立 , 即   =   ,∠ AMB =90 ° . 如图所示 , 当点 C 与点 M 重合时 , AC 1 , AC 2 的长即为所求 .   思路分析     (1)证明△ AOC ≌△ BOD ,得 AC = BD ,∠ OAC =∠ OBD , ∠ AMB =∠ AOB =40 ° ;(2)证明 △ AOC ∽△ BOD ,得   =   =   ,∠ OAC =∠ OBD ,∠ AMB =∠ AOB =90 ° ;(3)作图确定△ OCD 旋 转后点 C 的两个位置,分别求出 BD 的长度,根据   =   得出 AC 的长. 方法规律     本题为类比探究拓展问题,首先根据题(1)中的特例感知解决问题的方法,类比探 究,可以类比(1)中解法,解(2)中的问题,得出结论,总结解答前两个问题所用的方法和所得结论, 依据结论对(3)中的问题分析,通过作图,计算得出结果.问题(3)直接求 AC 的两个值难度较大,可 以先求出 BD 的两个值,根据   =   ,再求出 AC 的两个值. 5. (2018山西,21,8分)请阅读下列材料,并完成相应的任务. 在数学中 , 利用图形在变化过程中的不变性质 , 常常可以找到解决问题的办法 . 著名美籍匈牙利数学家波利亚在他所著的 《 数学的发现 》 一书中有这样一个例子 : 试问如何在一个三角形 ABC 的 AC 和 BC 两边上分别取一点 X 和 Y , 使得 AX = BY = XY ( 如图 ). 解决这个问题的操作步骤如 下 : 第一步 , 在 CA 上作出一点 D , 使得 CD = CB , 连接 BD . 第二步 , 在 CB 上取一点 Y ', 作 Y ' Z '∥ CA , 交 BD 于点 Z ', 并在 AB 上取一点 A ', 使 Z ' A '= Y ' Z '. 第三步 , 过点 A 作 AZ ∥ A ' Z ', 交 BD 于点 Z . 第四步 , 过点 Z 作 ZY ∥ AC , 交 BC 于点 Y , 再过点 Y 作 YX ∥ ZA , 交 AC 于点 X . 则有 AX = BY = XY . 下面是该结论的部分证明 : 证明 :∵ AZ ∥ A ' Z ', ∴∠ BA ' Z '=∠ BAZ , 又∵∠ A ' BZ '=∠ ABZ , ∴△ BA ' Z '∽△ BAZ . ∴   =   . 同理可得   =   . ∴   =   . ∵ Z ' A '= Y ' Z ',∴ ZA = YZ . … 任务:(1)请根据上面的操作步骤及部分证明过程,判断四边形 AXYZ 的形状,并加以证明; (2)请再仔细阅读上面的 操作步骤 ,在(1)的基础上完成 AX = BY = XY 的证明过程; (3)上述解决问题的过程中,通过作平行线把四边形 BA ' Z ' Y '放大得到四边形 BAZY ,从而确定了 点 Z , Y 的位置,这里运用了下面一种图形的变化是 　　　     . A.平移　    B.旋转　    C.轴对称　    D.位似 解析 　 (1) 四边形 AXYZ 是菱形 .   (1 分 ) 证明 :∵ ZY ∥ AC , YX ∥ ZA , ∴ 四边形 AXYZ 是平行四边形 .   (2 分 ) ∵ ZA = YZ , ∴ ▱ AXYZ 是菱形 .   (3 分 ) (2) 证明 :∵ CD = CB , ∴∠1=∠2.   (4 分 ) ∵ ZY ∥ AC , ∴∠1=∠3.   (5 分 ) ∴∠2=∠3,∴ YB = YZ .   (6 分 ) ∵ 四边形 AXYZ 是菱形 ,∴ AX = XY = YZ . ∴ AX = BY = XY .   (7 分 )   (3)D(或位似).   (8分) 解题关键     认真阅读文章,理解解题的思路和方法,并学会探究解题的原理. 6. (2017吉林,20,7分)图①、图②、图③都是由边长为1的小等边三角形构成的网格,每个小等 边三角形的顶点称为格点.线段 AB 的端点在格点上. (1)在图①、图②中,以 AB 为边各画一个等腰三角形,且第三个顶点在格点上;(所画图形不全 等) (2)在图③中,以 AB 为边画一个平行四边形,且另外两个顶点在格点上.   解析 　(1)每画对一个得2分.答案不唯一,以下答案供参考.   (2)画对一个即可.答案不唯一,以下答案供参考.   7. (2017吉林,23,8分)如图①, BD 是矩形 ABCD 的对角线,∠ ABD =30 ° , AD =1.将△ BCD 沿射线 BD 方向平移到△ B ' C ' D '的位置,使 B '为 BD 中点,连接 AB ', C ' D , AD ', BC ',如图②. (1)求证:四边形 AB ' C ' D 是菱形; (2)四边形 ABC ' D '的周长为 　　　     ; (3)将四边形 ABC ' D '沿它的两条对角线剪开,用得到的四个三角形拼成与其面积相等的矩形,直 接写出所有可能拼成的矩形周长.   解析 　 (1) 证明 :∵ 四边形 ABCD 是矩形 ,∴ AD ∥ BC , AD = BC . 易知 AD ∥ B ' C ', AD = B ' C '. ∴ 四边形 AB ' C ' D 为平行四边形 . ∵∠ DAB =90 ° ,∠ ABD =30 ° ,∴ AD =   BD . ∵ B ' 为 BD 中点 ,∴ AB '=   BD . ∴ AD = AB '. ∴ 四边形 AB ' C ' D 为菱形 . (2)∵∠ DAB =90 ° ,∠ ABD =30 ° ,∴ BD =2,∴ AB =   . 易证 ABC ' D ' 是菱形 . ∴ 四边形 ABC ' D ' 的周长是 4   . (3) 如图 .   周长为2 ×   =6+   . 如图.   周长为2 ×   =3+2   . 8. (2017江西,16,6分)如图,已知正七边形 ABCDEFG ,请   ,分别按下列要求画图. (1)在图1中,画出一个以 AB 为边的平行四边形; (2)在图2中,画出一个以 AF 为边的菱形.   解析 　(1)如图.(画法有多种,正确画出一种即可,以下几种画法仅供参考)     (2)如图.(画法有两种,正确画出其中一种即可)   9. (2016山西,22,12分)综合与实践 问题情境 在综合与实践课上,老师让同学们以“菱形纸片的剪拼”为主题开展数学活动.如图1,将一张 菱形纸片 ABCD (∠ BAD >90 ° )沿对角线 AC 剪开,得到△ ABC 和△ ACD .   操作发现 (1)将图1中的△ ACD 以 A 为旋转中心,按逆时针方向旋转角 α ,使 α =∠ BAC ,得到如图2所示的 △ AC ' D ,分别延长 BC 和 DC '交于点 E ,则四边形 ACEC '的形状是 　　　     ; (2)创新小组将图1中的△ ACD 以 A 为旋转中心,按逆时针方向旋转角 α ,使 α =2∠ BAC ,得到如图3 所示的△ AC ' D ,连接 DB , C ' C ,得到四边形 BCC ' D ,发现它是矩形.请你证明这个结论; 实践探究 (3)缜密小组在创新小组发现结论的基础上,量得图3中 BC =13 cm, AC =10 cm,然后提出一个问 题:将△ AC ' D 沿着射线 DB 方向平移 a cm,得到△ A ' C ″ D ',连接 BD ', CC ″,使四边形 BCC ″ D '恰 好为正方形,求 a 的值.请你解答此问题; (4)请你参照以上操作,将图1中的△ ACD 在同一平面内进行一次平移,得到△ A ' C ' D ,在图4中画 出平移后构造出的新图形,标明字母,说明平移及构图方法,写出你发现的结论,不必证明.   图4 解析 　 (1) 菱形 . (2) 证明 : 如图 , 作 AE ⊥ CC ' 于点 E .   由旋转得 AC '= AC ,∴∠ CAE =∠ C ' AE =   α =∠ BAC . 由题意知 BA = BC ,∴∠ BCA =∠ BAC . ∴∠ CAE =∠ BCA ,∴ AE ∥ BC . 同理 , AE ∥ DC ',∴ BC ∥ DC '. 又∵ BC = DC ',∴ 四边形 BCC ' D 是平行四边形 . 又∵ AE ∥ BC ,∠ CEA =90 ° , ∴∠ BCC '=180 ° -∠ CEA =90 ° , ∴ 四边形 BCC ' D 是矩形 . (3) 过点 B 作 BF ⊥ AC , 垂足为 F . ∵ BA = BC ,∴ CF = AF =   AC =   × 10=5(cm). 在 Rt△ BCF 中 , BF =   =   =12(cm). 在△ ACE 和△ CBF 中 ,∵∠ CAE =∠ BCF ,∠ CEA =∠ BFC =90 ° ,∴△ ACE ∽△ CBF . ∴   =   , 即   =   , 解得 CE =   . 当四边形 BCC ″ D ' 恰好为正方形时 , 分两种情况 : ① 点 C ″ 在边 C ' C 上 , a = C ' C -13=   -13=   . ② 点 C ″ 在 C ' C 的延长线上 , a = C ' C +13=   +13=   . 综上所述 , a 的值为   或   . (4) 答案不唯一 . 例 : 如图 .   平移及构图方法:将△ ACD 沿着射线 CA 方向平移,平移距离为   AC 的长度,得到△ A ' C ' D ,连接 A ' B , DC . 结论:四边形 A ' BCD 是平行四边形. 10. (2016山东青岛,23,10分)问题提出:如何将边长为 n ( n ≥ 5,且 n 为整数)的正方形分割为一些1 × 5或2 × 3的矩形( a × b 的矩形指边长分别为 a , b 的矩形)? 问题探究:我们先从简单的问题开始研究解决,再把复杂问题转化为已解决的问题. 探究一: 如图①,当 n =5时,可将正方形分割为五个1 × 5的矩形. 如图②,当 n =6时,可将正方形分割为六个2 × 3的矩形. 如图③,当 n =7时,可将正方形分割为五个1 × 5的矩形和四个2 × 3的矩形. 如图④,当 n =8时,可将正方形分割为八个1 × 5的矩形和四个2 × 3的矩形. 如图⑤,当 n =9时,可将正方形分割为九个1 × 5的矩形和六个2 × 3的矩形.   探究二: 当 n =10,11,12,13,14时,分别将正方形按下列方式分割:   所以,当 n =10,11,12,13,14时,均可将正方形分割为一个5 × 5的正方形、一个( n -5) × ( n -5)的正方形 和两个5 × ( n -5)的矩形.显然,5 × 5的正方形和5 × ( n -5)的矩形均可分割为1 × 5的矩形,而( n -5) × ( n -5) 的正方形是边长分别为5,6,7,8,9的正方形,用探究一的方法可分割为一些1 × 5或2 × 3的矩形. 探究三: 当 n =15,16,17,18,19时,分别将正方形按下列方式分割:   请按照上面的方法,分别画出边长为18,19的正方形分割示意图. 所以,当 n =15,16,17,18,19时,均可将正方形分割为一个10 × 10的正方形、一个( n -10) × ( n -10)的正 方形和两个10 × ( n -10)的矩形.显然,10 × 10的正方形和10 × ( n -10)的矩形均可分割为1 × 5的矩形, 而( n -10) × ( n -10)的正方形又是边长分别为5,6,7,8,9的正方形,用探究一的方法可分割为一些1 × 5或2 × 3的矩形. 问题解决:如何将边长为 n ( n ≥ 5,且 n 为整数)的正方形分割为一些1 × 5或2 × 3的矩形?请按照上面 的方法画出分割示意图,并加以说明. 实际应用:如何将边长为61的正方形分割为一些1 × 5或2 × 3的矩形?(只需按照探究三的方法画 出分割示意图即可) 解析     探究三:   问题解决: 当正方形的边长为 n ( n ≥ 5,且 n 为整数)时,按下图方式,均可将正方形分割为一个5 m × 5 m 的正方 形、一个( n -5 m ) × ( n -5 m )的正方形和两个5 m × ( n -5 m )的矩形.显然,5 m × 5 m 的正方形和5 m × ( n -5 m ) 的矩形均可分割为1 × 5的矩形,而( n -5 m ) × ( n -5 m )的正方形又是边长分别为5,6,7,8,9的正方形,用 探究一的方法可分割为一些1 × 5或2 × 3的矩形.   实际应用:   思路分析      n =15、16、17时,发现规律:左上10 × 10,左下10 × ( n -10),右上10 × ( n -10),右下( n -10)( n - 10),从而画出 n =18、19时的分割示意图.进而得到一般规律,解决其他问题. 解题关键     通过前面的示例发现规律,并利用规律解决问题. 11. (2015福建福州,24,12分)定义:长宽比为   ∶1( n 为正整数)的矩形称为   矩形. 下面,我们通过折叠的方式折出一个   矩形,如图①所示. 操作1:将正方形 ABCD 沿过点 B 的直线折叠,使折叠后的点 C 落在对角线 BD 上的点 G 处,折痕为 BH . 操作2:将 AD 沿过点 G 的直线折叠,使点 A ,点 D 分别落在边 AB , CD 上,折痕为 EF . 则四边形 BCEF 为   矩形.   图① 证明:设正方形 ABCD 的边长为1,则 BD =   =   . 由折叠性质可知 BG = BC =1,∠ AFE =∠ BFE =90 ° ,则四边形 BCEF 为矩形, ∴∠ A =∠ BFE . ∴ EF ∥ AD . ∴   =   , 即   =   . ∴ BF =   . ∴ BC ∶ BF =1∶   =   ∶1. ∴ 四边形 BCEF 为   矩形 . 阅读以上内容 , 回答下列问题 : (1) 在图①中 , 所有与 CH 相等的线段是 　　　     ,tan∠ HBC 的值是 　　　     ; (2) 已知四边形 BCEF 为   矩形 , 模仿上述操作 , 得到四边形 BCMN , 如图② , 求证 : 四边形 BCMN 是   矩形 ; (3) 将图②中的   矩形 BCMN 沿用 (2) 中的方式操作 3 次后 , 得到一个“   矩形” , 则 n 的值是      　　     .   图②　　 解析 　 (1) GH , DG ;   -1. (2) 证明 :∵ BF =   , BC =1,∴ BE =   =   . 由折叠性质可知 BP = BC =1,∠ FNM =∠ BNM =90 ° , 则四边形 BCMN 为矩形 , ∴∠ BNM =∠ F . ∴ MN ∥ EF . ∴   =   , 即 BP · BF = BE · BN . ∴   BN =   .∴ BN =   . ∴ BC ∶ BN =1∶   =   ∶1. ∴ 四边形 BCMN 是   矩形 . (3)6. 思路分析     (1)通过折叠可得 GH = HC ,通过证△ DGH 是等腰直角三角形可得 GD = GH .(2)根据 题中证明过程可证.(3)利用折叠性质得到相等的线段,相等的角,进而证明四边形 BCMN 为矩 形,利用平行线分线段成比例求矩形的长宽比,即得 n 的值. 解题关键     要关注矩形的长和宽的数量关系.