- 2021-05-10 发布 |
- 37.5 KB |
- 10页

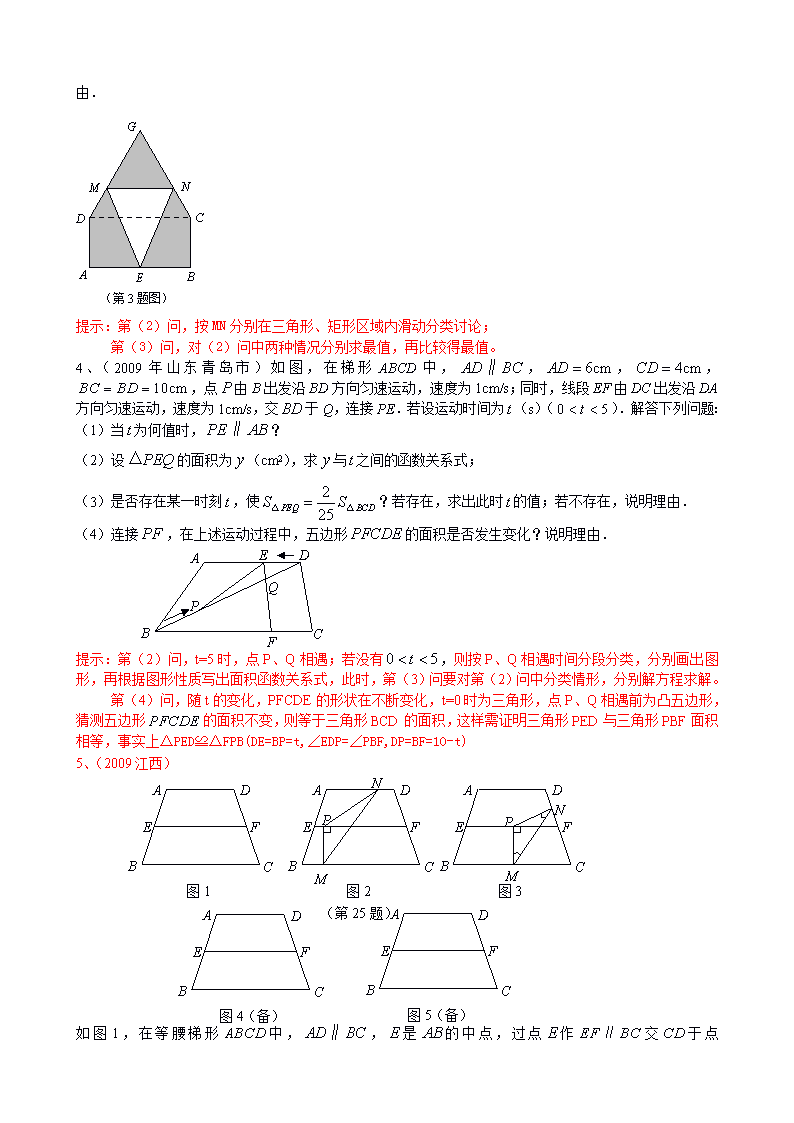

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
中考数学压轴题五平移问题
平移问题 平移性质——平移前后图形全等,对应点连线平行且相等。 一、直线的平移 1、(2009武汉)如图,直线与双曲线()交于点.将直线向右平移个单位后,与双曲线()交于点,与轴交于点,若,则 . O x y A B C 2、(09年四川南充市)如图已知正比例函数和反比例函数的图象都经过点. (1)求正比例函数和反比例函数的解析式; (2)把直线OA向下平移后与反比例函数的图象交于点,求的值和这个一次函数的解析式; (3)第(2)问中的一次函数的图象与轴、轴分别交于C、D,求过A、B、D三点的二次函数的解析式; (4)在第(3)问的条件下,二次函数的图象上是否存在点E,使四边形OECD的面积与四边形OABD的面积S满足:?若存在,求点E的坐标;若不存在,请说明理由. y x O C D B A 3 3 6 提示:第(2)问,直线平行时,解析式中k值相等。 3、(2009年日照)某仓库为了保持库内的湿度和温度,四周墙上均装有如图所示的自动通风设施.该设施的下部ABCD是矩形,其中AB=2米,BC=1米;上部CDG是等边三角形,固定点E为AB的中点.△EMN是由电脑控制其形状变化的三角通风窗(阴影部分均不通风),MN是可以沿设施边框上下滑动且始终保持和AB平行的伸缩横杆. (1)当MN和AB之间的距离为0.5米时,求此时△EMN的面积; (2)设MN与AB之间的距离为米,试将△EMN的面积S(平方米)表示成关于x的函数; (3)请你探究△EMN的面积S(平方米)有无最大值,若有,请求出这个最大值;若没有, 请说明理由. E A B G N D M C (第3题图) 提示:第(2)问,按MN分别在三角形、矩形区域内滑动分类讨论; 第(3)问,对(2)问中两种情况分别求最值,再比较得最值。 4、(2009年山东青岛市)如图,在梯形ABCD中,,,,,点由B出发沿BD方向匀速运动,速度为1cm/s;同时,线段EF由DC出发沿DA方向匀速运动,速度为1cm/s,交于Q,连接PE.若设运动时间为(s)().解答下列问题: (1)当为何值时,? (2)设的面积为(cm2),求与之间的函数关系式; (3)是否存在某一时刻,使?若存在,求出此时的值;若不存在,说明理由. (4)连接,在上述运动过程中,五边形的面积是否发生变化?说明理由. A E D Q P B F C 提示:第(2)问,t=5时,点P、Q相遇;若没有,则按P、Q相遇时间分段分类,分别画出图形,再根据图形性质写出面积函数关系式,此时,第(3)问要对第(2)问中分类情形,分别解方程求解。 第(4)问,随t的变化,PFCDE的形状在不断变化,t=0时为三角形,点P、Q相遇前为凸五边形,猜测五边形的面积不变,则等于三角形BCD的面积,这样需证明三角形PED与三角形PBF面积相等,事实上△PED≌△FPB(DE=BP=t,∠EDP=∠PBF,DP=BF=10-t) 5、(2009江西) A D E B F C 图4(备)用) A D E B F C 图5(备) 备用) A D E B F C 图1 图2 A D E B F C P N M 图3 A D E B F C P N M (第25题) 如图1,在等腰梯形中,,是的中点,过点作交于点 .,. (1)求点到的距离; (2)点为线段上的一个动点,过作交于点,过作交折线于点,连结,设. ①当点在线段上时(如图2),的形状是否发生改变?若不变,求出的周长;若改变,请说明理由; ②当点在线段上时(如图3),是否存在点,使为等腰三角形?若存在,请求出所有满足要求的的值;若不存在,请说明理由. 提示:第(2)①问,找特殊位置——点N 与点D重合时,易求周长; 第(2)②问,分三种情形,都要找图形的特性,△MNC恒为正三角形; (一)PN=PM时,PN⊥DC; (二)PM=MN时,PM⊥EF,PM=MN=MC; (三)PN=MN时,PM⊥EF,P与F重合; 6、(2009年长春)如图,直线分别与轴、轴交于两点,直线与交于点,与过点且平行于轴的直线交于点.点从点出发,以每秒1个单位的速度沿轴向左运动.过点作轴的垂线,分别交直线于两点,以为边向右作正方形,设正方形与重叠部分(阴影部分)的面积为(平方单位).点的运动时间为(秒). (1)求点的坐标. (2)当时,求与之间的函数关系式.(4分) (3)求(2)中的最大值。 (4)当时,直接写出点在正方形内部时的取值范围. y x D N M Q B C O P E A (分析)(4)在正方形PQMN内部 即在QM 下且在 QP右 7、(09湖南邵阳)如图(8),直线的解析式为,它与轴、轴分别相交于两点.平行于直线的直线从原点出发,沿轴的正方形以每秒1个单位长度的速度运动,它与轴、轴分别相交于两点,设运动时间为秒(). (1)求两点的坐标; (2)用含的代数式表示的面积; (3)以为对角线作矩形,记和重合部分的面积为, ①当时,试探究与之间的函数关系式; ②在直线的运动过程中,当为何值时,为面积的? 提示:第(3)问,按 重叠图形分段分类 O M A P N y l m x B O M A P N y l m x B E P F 图8 ----------五边形、三角形。 二、三角形的平移 8、(2009威海)如图,△ABC和的△DEF是等腰直角三角形,∠C=∠F=90°,AB=2.DE=4.点B与点D重合,点A,B(D),E在同一条直线上,将△ABC沿方向平移,至点A与点E重合时停止.设点B,D之间的距离为x,△ABC与△DEF重叠部分的面积为y,则准确反映y与x之间对应关系的图象是( ) 9、(2009年济南)如图,点G、D、C在直线a上,点E、F、A、B在直线b上,若从如图所示的位置出发,沿直线b向右匀速运动,直到EG与BC重合.运动过程中与矩形重合部分的面积(S)随时间(t)变化的图象大致是( ) C B A D (第9题) G D C E F A B b a (第7题图) s t O A. s t O B. C. s t O D. s t O 10、(2009年山东青岛市)已知:如图,在中,AE是BC边上的高,将沿方向平移,使点E与点C重合,得. (1)求证:; (2)若,当AB与BC满足什么数量关系时,四边形是菱形?证明你的结论. A D G C B F E 第8题图 , 11、(2009年咸宁市)如图,将矩形沿对角线剪开,再把沿方向平移得到. (1)证明; (2)若,试问当点在线段上的什么位置时,四边形是菱形,并请说明理由. 三、四边形的平移 12、(2009年山西省)如图,已知直线与直线相交于点分别交轴于两点.矩形的顶点分别在直线上,顶点都在轴上,且点与点重合. (1)求的面积; (2)求矩形的边与的长; (3)若矩形从原地出发,沿轴的反方向以每秒1个单位长度的速度平移,设移动时间为秒,矩形与重叠部分的面积为,求关于的函数关系式,并写出相应的的取值范围. A D B E O C F x y y (G) 提示:第(3)问,找准平移过程中的几个临界位置分段分类-----DG过点C,EF过点A;按重叠图形种类分段分类——五边形、四边形、三角形。 13、(2009年衡阳市) B x y M C D O A 图(1) B x y O A 图(2) B x y O A 图(3) 如图,直线与两坐标轴分别相交于A、B点,点M是线段AB上任意一点(A、B两点除外),过M分别作MC⊥OA于点C,MD⊥OB于D. (1)当点M在AB上运动时,你认为四边形OCMD的周长是否发生变化?并说明理由; (2)当点M运动到什么位置时,四边形OCMD的面积有最大值?最大值是多少? (3)当四边形OCMD为正方形时,将四边形OCMD沿着x轴的正方向移动,设平移的距离为,正方形OCMD与△AOB重叠部分的面积为S.试求S与的函数关系式并画出该函数的图象. 提示:第(3)问,按 重叠图形分段分类 ----------五边形、三角形。 14、(湖南2009年娄底市)如图11,在△ABC中,∠C=90°,BC=8,AC=6,另有一直角梯形DEFH(HF∥DE,∠HDE=90°)的底边DE落在CB上,腰DH落在CA上,且DE=4,∠DEF=∠CBA,AH∶AC=2∶3 (1)延长HF交AB于G,求△AHG的面积.(2)操作:固定△ABC,将直角梯形DEFH以每秒1个单位的速度沿CB方向向右移动,直到点D与点B重合时停止,设运动的时间为t秒,运动后的直角梯形为DEFH′(图12). 探究1:在运动中,四边形CDH′H能否为正方形?若能, 请求出此时t的值;若不能,请说明理由. 探究2:在运动过程中,△ABC与直角梯形DEFH′重叠部分的面积为y,求y与t的函数关系. 提示:探究2中平移临界位置---F与G重合,H与G重合。 四、圆的平移问题 15、(2009年江苏省)如图,已知射线DE与轴和轴分别交于点和点.动点从点出发,以1个单位长度/秒的速度沿轴向左作匀速运动,与此同时,动点P从点D出发,也以1个单位长度/秒的速度沿射线DE的方向作匀速运动.设运动时间为秒. (1)请用含的代数式分别表示出点C与点P的坐标; (2)以点C为圆心、个单位长度为半径的与轴交于A、B两点 (点A在点B的左侧),连接PA、PB. ①当与射线DE有公共点时,求的取值范围; ②当为等腰三角形时,求的值. 提示: 第(2)①问,找特殊位置——A与D重合,⊙C与射线相切 第(2)②问,分类讨论:方法一(解析法)——用勾股定理表示出PA、PB、AB的长,解方程求出t值;方法二(几何法)——按时间过程分别画出满足要求的图形再由图中性质求t值,有四种情形, PA=PB,PB=AB, PA=PB,PA=PD=AB。 16、(2009年云南省) 已知在平面直角坐标系中,四边形OABC是矩形,点A、C的坐标分别为、,点D的坐标为,点P是直线AC上的一动点,直线DP与轴交于点M.问: (1)当点P运动到何位置时,直线DP平分矩形OABC的面积,请简要说明理由,并求出此时直线DP的函数解析式; (2)当点P沿直线AC移动时,是否存在使与相似的点M,若存在,请求出点M的坐标;若不存在,请说明理由; (3)当点P沿直线AC移动时,以点P为圆心、半径长为R(R>0)画圆,所得到的圆称为动圆P.若设动圆P的直径长为AC,过点D作动圆P的两条切线,切点分别为点E、F.请探求是否存在四边形DEPF的最小面积S,若存在,请求出S的值;若不存在,请说明理由. 提示:第(2)问,三种情形; 第(3)问,过点D作AC垂线,垂足为P,以AC长为直径画圆,证明此时面积最小。 备用图 四、抛物线的平移 17、(2009年舟山)如图,已知点A(-4,8)和点B(2,n)在抛物线上. (1) 求a的值及点B关于x轴对称点P的坐标,并在x轴上找一点Q,使得AQ+QB最短,求出点Q的坐标; (2) 平移抛物线,记平移后点A的对应点为A′,点B的对应点为B′,点C(-2,0)和点D(-4,0)是x轴上的两个定点. ① 当抛物线向左平移到某个位置时,A′C+CB′ 最短,求此时抛物线的函数解析式; ② 当抛物线向左或向右平移时,是否存在某个位置,使四边形A′B′CD的周长最短?若存在,求出此时抛物线的函数解析式;若不存在,请说明理由. 4 x 2 2 A 8 -2 O -2 -4 y 6 B C D -4 4 Q P 提示: 第(2)问,是轴对称的运用。抛物线左移 ① 方法一,A′关于x轴对称点A〞,要使 A′C+CB′最短,点C应在直线A〞B′上; 方法二,由(1)知,此时事实上,点Q移到点C位置,求CQ=14/5,即抛物线左移14/5单位; ②设抛物线左移b个单位,则A'(-4-b,8)、B'(2-b,2)。∵CD=2,∴B'左移2个单位得到B″(-b,2)位置,要使A′D+C B'最短,只要A′D+DB″最短。则只有点D在直线 ((2)①图) 4 x 2 2 A′ 8 -2 O -2 -4 y 6 B′ C D -4 4 A′′ A″B″上。 ((2)②图) 4 x 2 2 A′ 8 -2 O -2 -4 y 6 B′ C D -4 4 A′′ B′′ 18、(2009年北京市)已知关于的一元二次方程有实数根,为正整数. (1)求的值; (2)当此方程有两个非零的整数根时,将关于的二次函数的图象向下平移8个单位,求平移后的图象的解析式; (3)在(2)的条件下,将平移后的二次函数的图象在轴下方的部分沿轴翻折,图象的其余部分保持不变,得到一个新的图象.请你结合这个新的图象回答:当直线 与此图象有两个公共点时,的取值范围. 19、(2009年湖北省荆门市)一开口向上的抛物线与x轴交于A(m-2,0),B(m+2,0)两点,记抛物线顶点为C,且AC⊥BC. (1)若m为常数,求抛物线的解析式; (2)若m为小于0的常数,那么(1)中的抛物线经过怎么样的平移可以使顶点在坐标原点? (3)设抛物线交y轴正半轴于D点,问是否存在实数m,使得△BCD为等腰三角形?若存在,求出m的值;若不存在,请说明理由. 第15题图 20(09湖北宜昌)已知:直角梯形OABC的四个顶点是O(0,0),A(,1), B(s,t),C(,0),抛物线y=x2+mx-m的顶点P是直角梯形OABC内部或边上的一个动点,m为常数. (1)求s与t的值,并在直角坐标系中画出直角梯形OABC; (2)当抛物线y=x2+mx-m与直角梯形OABC的边AB相交时,求m的取值范围. 提示:第(2)问,满足两个条件, (一) 先求顶点P坐标,再由其活动范围确定m取值范围,P在AB下,x轴上,线段OA右,BC左; (二) 抛物线与线段AB有交点,得到一个特殊方程,求出两解,再求M范围。 21、(2009浙江省杭州市) 已知平行于x轴的直线与函数和函数的图象分别交于点A和点B,又有定点P(2,0)。 (1)若,且tan∠POB=,求线段AB的长; (2)在过A,B两点且顶点在直线上的抛物线中,已知线段AB=,且在它的对称轴左边时,y随着x的增大而增大,试求出满足条件的抛物线的解析式; (3)已知经过A,B,P三点的抛物线,平移后能得到的图象,求点P到直线AB的距离。 22、(2009年台州市) (第17题) 如图,已知直线 交坐标轴于两点,以线段为边向上作正方形,过点的抛物线与直线另一个交点为. (1)请直接写出点的坐标; (2)求抛物线的解析式; (3)若正方形以每秒个单位长度的速度沿射线下滑,直至顶点落在轴上时停止.设正方形落在轴下方部分的面积为,求关于滑行时间的函数关系式,并写出相应自变量的取值范围; (4)在(3)的条件下,抛物线与正方形一起平移,同时停止,求抛物线上两点间的抛物线弧所扫过的面积.查看更多