中考数学复习与圆有关的最值取值范围问题专练无答案

中考数学复习与圆有关的最值取值范围问题专练无答案

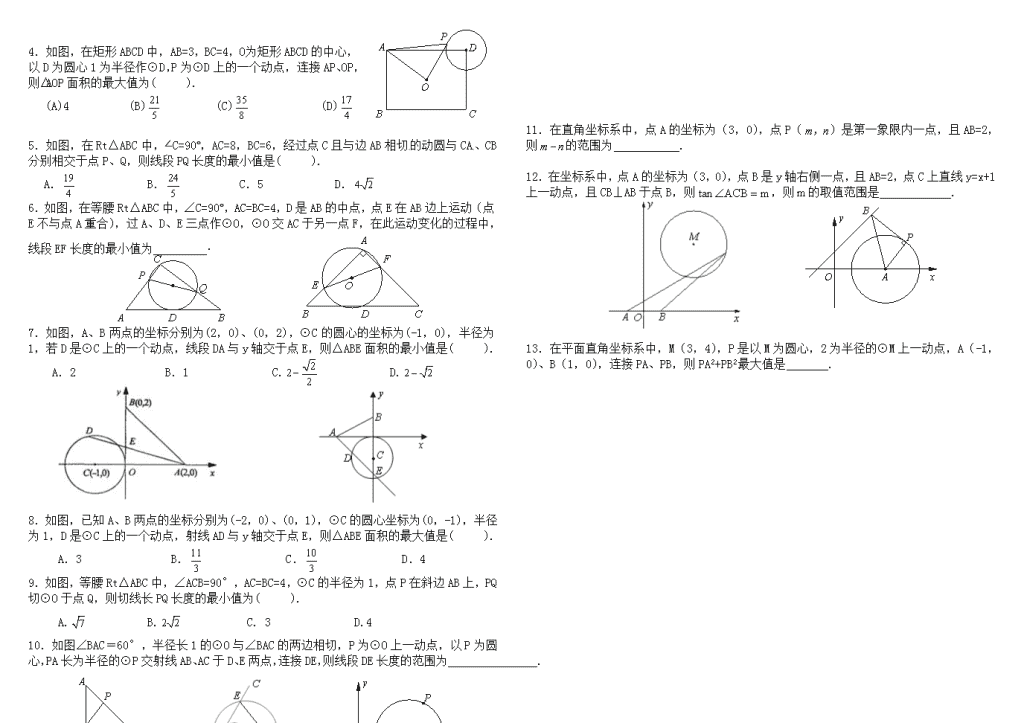
与圆有关的最值（取值范围）问题 解题策略 ‎1．直观感觉，画出图形；‎ ‎2．特殊位置，比较结果；‎ ‎ 3．理性分析动点过程中所维系的不变条件，通过几何构建，寻找动量与定量（常量）之间的关系，建立等式，进行转化.‎ 例一、不等式、配方法 ‎1．如图，已知半径为2的⊙O与直线l相切于点A，点P是直径AB左侧半圆上的动点，过点P作直线l的垂线，垂足为C，PC与⊙O交于点D，连接PA、PB，设PC的长为x（2＜x＜4），则当x= 时，PD•CD的值最大，且最大值是为 .‎ ‎2．如图，线段AB=4，C为线段AB上的一个动点，以AC、BC为边作等边△ACD和等边△BCE，⊙O外接于△CDE，则⊙O半径的最小值为( ).‎ A.4 B. C. D. 2‎ ‎3．在平面直角坐标系中，以坐标原点O为圆心，2为半径画⊙O，P是⊙O上一动点，且P在第一象限内，过点P作⊙O的切线与轴相交于点A，与轴相交于点B，线段AB长度的最小值是 .‎ 例二、相切的应用（有公共点、最大或最小夹角）‎ ‎1．如图，在Rt△ABC中，∠C=90°，AC=6，BC=8，D为AB边上一点，过点D作CD的垂线交直线BC于点E，则线段CE长度的最小值是 .‎ ‎2．如图，Rt△ABC中，∠C=90°，∠A=30°，AB=4，以AC上的一点O为圆心OA为半径作⊙O，若⊙O与边BC始终有交点（包括B、C两点），则线段AO的取值范围是 .‎ ‎3．如图，射线PQ∥射线MN，PM⊥MN，A为PM的中点，O为射线PQ上的一个动点，AC⊥AB交MN于点C，当以O为圆心，以OB为半径的圆与线段PM有公共点时（包括P、M两点），则线段OP长度的最小值为 .‎ 例三、其他几何知识的运用 如图所示，AC⊥AB，AB=6，AC=4，点D是以AB为直径的半圆O上一动点，DE⊥CD交直线AB于点E，设∠DAB=，（0°＜＜90°）．若要使点E在线段OA上（包括O、A两点），则的取值范围为 .‎ 课堂练习：‎ ‎1．如图，已知直线l与⊙O相离，OA⊥l于点A，OA=5，OA与⊙O相交于点P，AB与⊙O相切于点B，BP的延长线交直线l于点C，若在⊙O上存在点Q，使△QAC是以AC为底边的等腰三角形，则⊙O的半径r的取值范围为 .‎ ‎2．已知：如图，RtΔABC中，∠B=90º，∠A=30º，BC=6cm，点O从A点出发，沿AB以每秒cm的速度向B点方向运动，当点O运动了t秒(t＞0)时，以O点为圆心的圆与边AC相切于点D，与边AB相交于E、F两点，过E作EG⊥DE交射线BC于G.‎ ‎（1）若点G在线段BC上，则t的取值范围是 ；‎ ‎（2）若点G在线段BC的延长线上，则t的取值范围是 .‎ ‎3．如图，⊙M，⊙N的半径分别为2cm，4cm，圆心距MN=10cm．P为⊙M上的任意一点，Q为⊙N上的任意一点，直线PQ与连心线所夹的锐角度数为，当P、Q在两圆上任意运动时，的最大值为( ).‎ ‎(A) (B) (C) (D)‎ ‎4．如图，在矩形ABCD中，AB=3，BC=4，O 为矩形ABCD的中心，以D为圆心1为半径作⊙D，P为⊙D上的一个动点，连接AP、OP，则△AOP面积的最大值为( ).‎ ‎ (A)4 (B) (C) (D)‎ ‎5．如图，在Rt△ABC中，∠C=90°，AC=8，BC=6，经过点C且与边AB相切的动圆与CA、CB分别相交于点P、Q，则线段PQ长度的最小值是( ).‎ A． B． C．5 D．‎ ‎6．如图，在等腰Rt△ABC中，∠C=90°，AC=BC=4，D是AB的中点，点E在AB边上运动（点E不与点A重合），过A、D、E三点作⊙O，⊙O交AC于另一点F，在此运动变化的过程中，线段EF长度的最小值为 ．‎ ‎7．如图，A、B两点的坐标分别为(2，0)、(0，2)，⊙C的圆心的坐标为(-1，0)，半径为1，若D是⊙C上的一个动点，线段DA与y轴交于点E，则△ABE面积的最小值是( ).‎ ‎ A．2 B．1 C. D.‎ ‎8．如图，已知A、B两点的坐标分别为(-2，0)、(0，1)，⊙C的圆心坐标为(0，-1)，半径为1，D是⊙C上的一个动点，射线AD与y轴交于点E，则△ABE面积的最大值是( ).‎ ‎ A．3 B． C． D．4‎ ‎9．如图，等腰Rt△ABC中，∠ACB=90°，AC=BC=4，⊙C的半径为1，点P在斜边AB上，PQ切⊙O于点Q，则切线长PQ长度的最小值为( ).‎ ‎ A. B. C. 3 D.4‎ ‎10．如图∠BAC＝60°，半径长1的⊙O与∠BAC的两边相切，P为⊙O上一动点，以P为圆心，PA长为半径的⊙P交射线AB、AC于D、E两点，连接DE，则线段DE长度的范围为 .‎ ‎11．在直角坐标系中，点A的坐标为（3，0），点P（）是第一象限内一点，且AB=2，则的范围为 .‎ ‎12．在坐标系中，点A的坐标为（3，0），点B是y轴右侧一点，且AB=2，点C上直线y=x+1上一动点，且CB⊥AB于点B，则，则的取值范围是 .‎ ‎ ‎ ‎13．在平面直角坐标系中，M（3，4），P是以M为圆心，2为半径的⊙M上一动点，A（-1，0）、B（1，0），连接PA、PB，则PA2+PB2最大值是 .‎