- 2021-05-10 发布 |
- 37.5 KB |
- 13页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
中考压轴题专题分类讲座七探究操作性问题
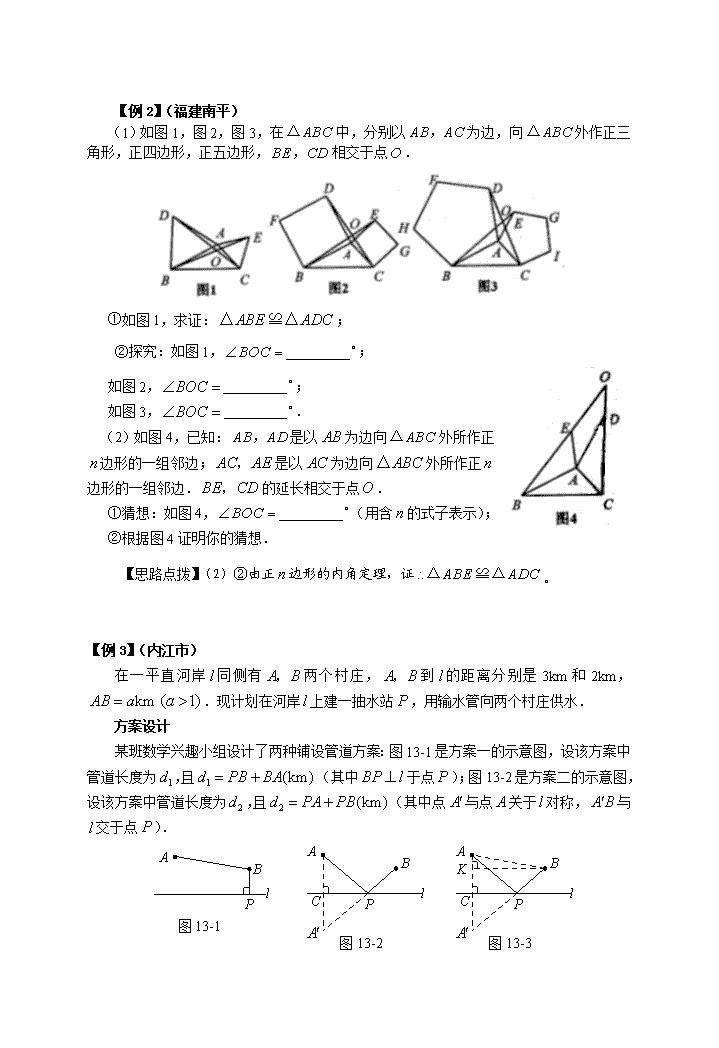
探究、操作性问题 【知识纵横】 探索研究是通过对题意的理解,解题过程由简单到难,在承上启下的作用下,引导学生思考新的问题,大胆进行分析、推理和归纳,即从特殊到一般去探究,以特殊去探求一般从而获得结论,有时还要用已学的知识加以论证探求所得结论。操作性问题是让学生按题目要求进行操作,考察学生的动手能力、想象能力和概括能力。 【典型例题】 【例1】(江苏镇江)探索研究 如图,在直角坐标系中,点为函数在第一象限内的图象上的任一 点,点的坐标为,直线过且与轴平行,过作轴的平行线分别交轴,于,连结交轴于,直线交轴于. (1)求证:点为线段的中点; (2)求证:①四边形为平行四边形; ②平行四边形为菱形; x l Q C P A O B H R y (3)除点外,直线与抛物线有无其它公共点?并说明理由. 【思路点拨】(2)①证;②设,证AP=PQ;(3)求直线的解析式与抛物线方程组成联立方程组,讨论方程组解的情况。 【例2】(福建南平) (1)如图1,图2,图3,在中,分别以为边,向外作正三角形,正四边形,正五边形,相交于点. ①如图1,求证:; ②探究:如图1, ; 如图2, ; 如图3, . (2)如图4,已知:是以为边向外所作正边形的一组邻边;是以为边向外所作正边形的一组邻边.的延长相交于点. ①猜想:如图4, (用含的式子表示); ②根据图4证明你的猜想. 【思路点拨】(2)②由正边形的内角定理,证。 【例3】(内江市) 在一平直河岸同侧有两个村庄,到的距离分别是3km和2km,.现计划在河岸上建一抽水站,用输水管向两个村庄供水. 方案设计 某班数学兴趣小组设计了两种铺设管道方案:图13-1是方案一的示意图,设该方案中管道长度为,且(其中于点);图13-2是方案二的示意图,设该方案中管道长度为,且(其中点与点关于对称,与交于点). A B P l l A B P C 图13-1 图13-2 l A B P C 图13-3 K 观察计算 (1)在方案一中, km(用含的式子表示); (2)在方案二中,组长小宇为了计算的长,作了如图13-3所示的辅助线,请你按小宇同学的思路计算, km(用含的式子表示). 探索归纳 (1)①当时,比较大小:(填“>”、“=”或“<”); ②当时,比较大小:(填“>”、“=”或“<”); 方法指导 当不易直接比较两个正数与的大小时,可以对它们的平方进行比较: ,, 与的符号相同. 当时,,即; 当时,,即; 当时,,即; (2)请你参考右边方框中的方法指导, 就(当时)的所有取值情况进 行分析,要使铺设的管道长度较短, 应选择方案一还是方案二? 【思路点拨】参考方法指导解答探索 归纳(2)。 【例4】(浙江宁波)如图1,把一张标准纸一次又一次对开,得到“2开”纸、“4开”纸、“8开”纸、“16开”纸….已知标准纸的短边长为. (1)如图2,把这张标准纸对开得到的“16开”张纸按如下步骤折叠: 第一步 将矩形的短边与长边对齐折叠,点落在上的点处,铺平后得折痕; 第二步 将长边与折痕对齐折叠,点正好与点重合,铺平后得折痕. 则的值是 ,的长分别是 , . (2)“2开”纸、“4开”纸、“8开”纸的长与宽之比是否都相等?若相等,直接写出这个比值;若不相等,请分别计算它们的比值. (3)如图3,由8个大小相等的小正方形构成“”型图案,它的四个顶点分别在“16开”纸的边上,求的长. (4)已知梯形中,,,,且四个顶点都在“4开” 纸的边上,请直接写出2个符合条件且大小不同的直角梯形的面积. A B C D B C A D E G H F F E 4开 2开 8开 16开 图1 图2 图3 (第26题) a 【思路点拨】(3)证,,设,建立关于x的方程解之;(4)参考图3分二类情形讨论。 【学力训练】 1、(山东聊城)探索研究:如图,把一张长10cm,宽8cm的矩形硬纸板的四周各剪 去一个同样大小的正方形,再折合成一个无盖的长方体盒子(纸板的厚度忽略不计). (1)要使长方体盒子的底面积为48cm2,那么剪去的正方形的边长为多少? (2)你感到折合而成的长方体盒子的侧面积会不会有更大的情况?如果有,请你求出最大值和此时剪去的正方形的边长;如果没有,请你说明理由; (3)如果把矩形硬纸板的四周分别剪去2个同样大小的正方形和2个同样形状、同样大小的矩形,然后折合成一个有盖的长方体盒子,是否有侧面积最大的情况;如果有,请你求出最大值和此时剪去的正方形的边长;如果没有,请你说明理由. 2、(山东枣庄)把一副三角板如图甲放置,其中,,,斜边,.把三角板DCE绕点C顺时针旋转15°得到△D1CE1(如图乙).这时AB与CD1相交于点,与D1E1相交于点F. (1)求的度数; (2)求线段AD1的长; (3)若把三角形D1CE1绕着点顺时针再旋转30°得△D2CE2,这时点B在△D2CE2 的内部、外部、还是边上?说明理由. B (乙) A E11 C D11 O F (甲) A C E D B 3、(江苏盐城)如图甲,在△ABC中,∠ACB为锐角.点D为射线BC上一动点,连接AD,以AD为一边且在AD的右侧作正方形ADEF. 解答下列问题: (1)如果AB=AC,∠BAC=90º. ①当点D在线段BC上时(与点B不重合),如图乙,线段CF、BD之间的位置 关系为 ▲ ,数量关系为 ▲ . 第28题图 图甲 图乙 图丙 ②当点D在线段BC的延长线上时,如图丙,①中的结论是否仍然成立,为什么? (2)如果AB≠AC,∠BAC≠90º,点D在线段BC上运动. 试探究:当△ABC满足一个什么条件时,CF⊥BC(点C、F重合除外)?画出相应图形,并说明理由.(画图不写作法) (3)若AC=,BC=3,在(2)的条件下,设正方形ADEF的边DE与线段CF 相交于点P,求线段CP长的最大值. 4、(07丽水市)如图,在平面直角坐标系中,直角梯形的边落在轴的正半轴上,且∥,,=4,=6,=8.正方形的两边分别落在坐标轴上,且它的面积等于直角梯形面积.将正方形沿轴的正半轴平行移动,设它与直角梯形的重叠部分面积为. (1)分析与计算: 求正方形的边长; (2)操作与求解: ①正方形平行移动过程中,通过操作、观察,试判断(>0)的变化情况是 ; A.逐渐增大 B.逐渐减少 C.先增大后减少 D.先减少后增大 ②当正方形顶点移动到点时,求的值; (3)探究与归纳: (备用图) A B C A B C O D E F 设正方形的顶点向右移动的距离为,求重叠部分面积与的函数关系式. 参考答案 【典型例题】 【例1】(江苏镇江)(1)由题可知. ,, . ,即为的中点. (2)①由(1)可知,, ,, . , 又,四边形为平行四边形. ②设,轴,则,则. 过作轴,垂足为,在中, . 平行四边形为菱形. (3)设直线为,由,得,代入得: 直线为. 设直线与抛物线的公共点为,代入直线关系式得: ,,解得.得公共点为. 所以直线与抛物线只有一个公共点. 【例2】(福建南平) (1)①证法一:与均为等边三角形, , 且 , 即 . ②,,. (2)① ②证法一:依题意,知和都是正边形的内角,,, ,即. . ,, 13分 , 【例3】(内江市) 观察计算 (1); (2). 探索归纳 (1)①;②; (2). ①当,即时,,.; ②当,即时,,.; ③当,即时,,.. 综上可知:当时,选方案二; 当时,选方案一或方案二; 当(缺不扣分)时,选方案一. 【例4】(浙江宁波) (1). (2)相等,比值为. (3)设, 在矩形中,, ,,, , . 同理. , , . , ,解得.即. (4), . 【学力训练】 1、(山东聊城)(1)设正方形的边长为cm,则 图1 图2 . 即. 解得(不合题意,舍去),. 剪去的正方形的边长为1cm. (注:通过观察、验证直接写出正确结果给3分) (2)有侧面积最大的情况. 设正方形的边长为cm,盒子的侧面积为cm2, 则与的函数关系式为: . 即. 改写为. 当时,. 即当剪去的正方形的边长为2.25cm时,长方体盒子的侧面积 最大为40.5cm2. (3)有侧面积最大的情况. 设正方形的边长为cm,盒子的侧面积为cm2. 若按图1所示的方法剪折,则与的函数关系式为: . 即. 当时,. 若按图2所示的方法剪折,则与的函数关系式为: . 即. 当时,. 比较以上两种剪折方法可以看出,按图2所示的方法剪折得到的盒子侧面积最大,即当剪去的正方形的边长为cm时,折成的有盖长方体盒子的侧面积最大,最大面积为cm2. 5 4 1 2 3 2、(山东枣庄) (1)如图所示,,, ∴. 又, ∴. (2),∴∠D1FO=60°. ,∴. 又,,∴. ,∴. 又,∴. 在中,. (3)点在内部. 理由如下:设(或延长线)交于点P,则. 在中,, ,即,∴点在内部. 3、(江苏盐城)(1)①CF与BD位置关系是 垂 直、数量关系是相 等; ②当点D在BC的延长线上时①的结论仍成立. 图丁 由正方形ADEF得 AD=AF ,∠DAF=90º. ∵∠BAC=90º,∴∠DAF=∠BAC , ∴∠DAB=∠FAC, 又AB=AC ,∴△DAB≌△FAC , ∴CF=BD ∠ACF=∠ABD. ∵∠BAC=90º, AB=AC ,∴∠ABC=45º,∴∠ACF=45º, ∴∠BCF=∠ACB+∠ACF= 90º.即 CF⊥BD (2)画图正确 当∠BCA=45º时,CF⊥BD(如图丁). 理由是:过点A作AG⊥AC交BC于点G,∴AC=AG 可证:△GAD≌△CAF ∴∠ACF=∠AGD=45º ∠BCF=∠ACB+∠ACF= 90º. 即CF⊥BD 图戊 (3)当具备∠BCA=45º时, 过点A作AQ⊥BC交BC的延长线于点Q,(如图戊) ∵DE与CF交于点P时, ∴此时点D位于线段CQ上, ∵∠BCA=45º,可求出AQ= CQ=4.设CD=x ,∴ DQ=4—x, 容易说明△AQD∽△DCP,∴ , ∴, . ∵0<x≤3 ∴当x=2时,CP有最大值1 A B C O D E F M N (如图①) 4、(07丽水市)(1)∵, 设正方形的边长为, ∴,或(舍去). (2). . (3)①当0≤<4时,重叠部分为三角形,如图①. 可得△∽△, A B C O D E F (如图②) ∴,=. ∴. ②当4≤<6时,重叠部分为直角梯形,如图②. . ③当6≤<8时,重叠部分为五边形,如图③. A B C O D E F M (如图③) 可得,,. =. ④当8≤<10时,重叠部分为五边形,如图④. =. ⑤当10≤≤14时,重叠部分为矩形,如图⑤. A B C O D E F (如图⑤) . A O B C D E F M (如图④) O查看更多