- 2021-05-10 发布 |
- 37.5 KB |
- 22页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
中考数学真题 尺规作图题型
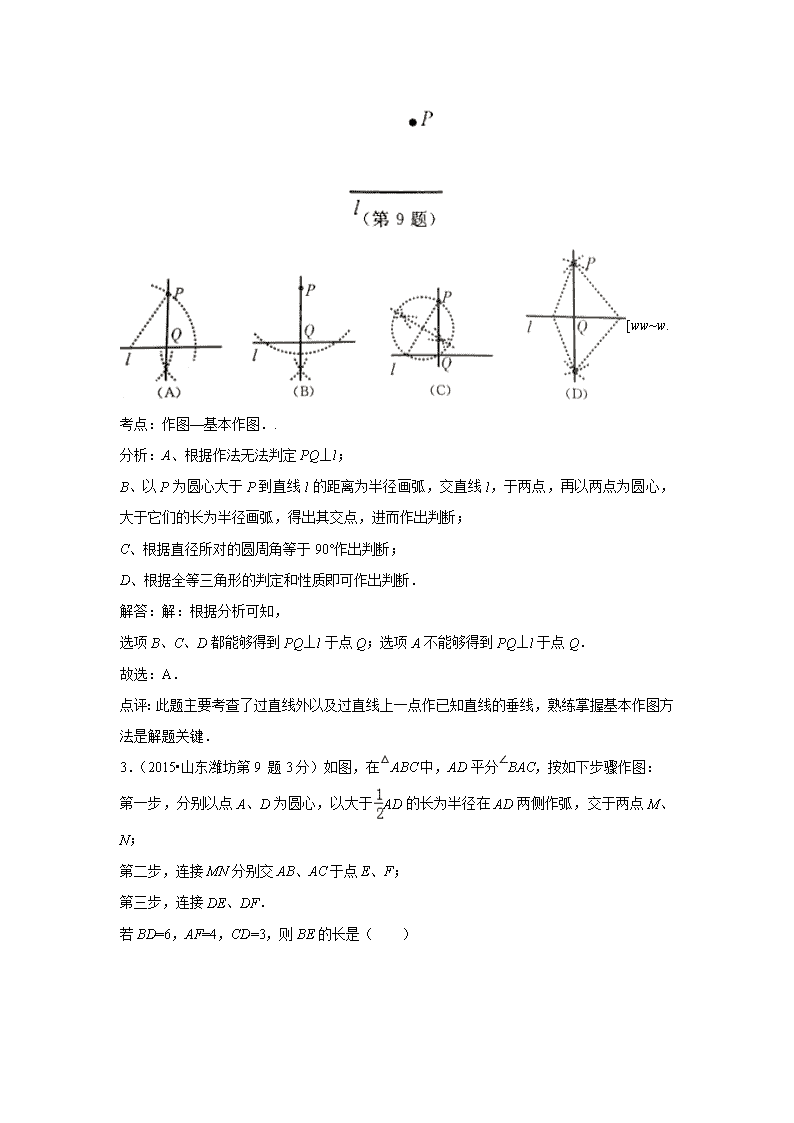
尺规作图 一.选择题 1. (2015•浙江衢州,第7题3分)数学课上,老师让学生尺规作图画,使其斜边 ,一条直角边.小明的作法如图所示,你认为这种作法中判断是直角的依据是【 】 A.勾股定理 B.直径所对的圆周角是直角 C.勾股定理的逆定理 D.90°的圆周角所对的弦是直径 【答案】B. 【考点】尺规作图(复杂作图);圆周角定理. 【分析】小明的作法是:①取,作的垂直平分线交于点; ②以点为圆心,长为半径画圆; ③以点为圆心,长为半径画弧,与交于点; ④连接. 则即为所求. 从以上作法可知,是直角的依据是:直径所对的圆周角是直角. 故选B. 2. (2015•浙江嘉兴,第9题4分)数学活动课上,四位同学围绕作图问题:“如图,已知直线l和l外一点P,用直尺和圆规作直线PQ,使PQ⊥l与点Q .”分别作出了下列四个图形. 其中做法错误的是(▲) [ww~w. 考点:作图—基本作图.. 分析:A、根据作法无法判定PQ⊥l; B、以P为圆心大于P到直线l的距离为半径画弧,交直线l,于两点,再以两点为圆心,大于它们的长为半径画弧,得出其交点,进而作出判断; C、根据直径所对的圆周角等于90°作出判断; D、根据全等三角形的判定和性质即可作出判断. 解答:解:根据分析可知, 选项B、C、D都能够得到PQ⊥l于点Q;选项A不能够得到PQ⊥l于点Q. 故选:A. 点评:此题主要考查了过直线外以及过直线上一点作已知直线的垂线,熟练掌握基本作图方法是解题关键. 3.(2015•山东潍坊第9 题3分)如图,在△ABC中,AD平分∠BAC,按如下步骤作图: 第一步,分别以点A、D为圆心,以大于AD的长为半径在AD两侧作弧,交于两点M、N; 第二步,连接MN分别交AB、AC于点E、F; 第三步,连接DE、DF. 若BD=6,AF=4,CD=3,则BE的长是( ) A. 2 B. 4 C. 6 D. 8 考点: 平行线分线段成比例;菱形的判定与性质;作图—基本作图.. 分析: 根据已知得出MN是线段AD的垂直平分线,推出AE=DE,AF=DF,求出DE∥AC,DF∥AE,得出四边形AEDF是菱形,根据菱形的性质得出AE=DE=DF=AF,根据平行线分线段成比例定理得出=,代入求出即可. 解答: 解:∵根据作法可知:MN是线段AD的垂直平分线, ∴AE=DE,AF=DF, ∴∠EAD=∠EDA, ∵AD平分∠BAC, ∴∠BAD=∠CAD, ∴∠EDA=∠CAD, ∴DE∥AC, 同理DF∥AE, ∴四边形AEDF是菱形, ∴AE=DE=DF=AF, ∵AF=4, ∴AE=DE=DF=AF=4, ∵DE∥AC, ∴=, ∵BD=6,AE=4,CD=3, ∴=, ∴BE=8, 故选D. 点评: 本题考查了平行线分线段成比例定理,菱形的性质和判定,线段垂直平分线性质,等腰三角形的性质的应用,能根据定理四边形AEDF是菱形是解此题的关键,注意:一组平行线截两条直线,所截得的对应线段成比例. 4.(2015•山东潍坊第9 题3分)如图,在△ABC中,AD平分∠BAC,按如下步骤作图: 第一步,分别以点A、D为圆心,以大于AD的长为半径在AD两侧作弧,交于两点M、N; 第二步,连接MN分别交AB、AC于点E、F; 第三步,连接DE、DF. 若BD=6,AF=4,CD=3,则BE的长是( ) A. 2 B. 4 C. 6 D. 8 考点: 平行线分线段成比例;菱形的判定与性质;作图—基本作图.. 分析: 根据已知得出MN是线段AD的垂直平分线,推出AE=DE,AF=DF,求出DE∥AC,DF∥AE,得出四边形AEDF是菱形,根据菱形的性质得出AE=DE=DF=AF,根据平行线分线段成比例定理得出=,代入求出即可. 解答: 解:∵根据作法可知:MN是线段AD的垂直平分线, ∴AE=DE,AF=DF, ∴∠EAD=∠EDA, ∵AD平分∠BAC, ∴∠BAD=∠CAD, ∴∠EDA=∠CAD, ∴DE∥AC, 同理DF∥AE, ∴四边形AEDF是菱形, ∴AE=DE=DF=AF, ∵AF=4, ∴AE=DE=DF=AF=4, ∵DE∥AC, ∴=, ∵BD=6,AE=4,CD=3, ∴=, ∴BE=8, 故选D. 点评: 本题考查了平行线分线段成比例定理,菱形的性质和判定,线段垂直平分线性质,等腰三角形的性质的应用,能根据定理四边形AEDF是菱形是解此题的关键,注意:一组平行线截两条直线,所截得的对应线段成比例. 二.填空题 1、(2015•四川自贡,第15题4分)如图,将线段放在边长为1的小正方形网格,点 点均落在格点上,请用无刻度直尺在线段上画出点, 使,并保留作图痕迹. 考点:矩形、正方形的性质、勾股定理、相似三角形的性质和判定. 分析:本题根据勾股定理可求出在网格中的,由于网格线中的对边平行,所以找点较容易,只需连接一对角线与的交点就满足(见图);根据的是平行线所截得相似三角形的对应边成比例, 所以 ,则. 略解:见图作法. 2.(2015•北京市,第16题,3分)阅读下面材料: 在数学课上,老师提出如下问题: 尺规作图:作一条线段的垂直平分线. 已知:线段AB. 小芸的作法如下: 如图, (1)分别以点A和点B为圆心,大于AB 的长为半径作弧,两弧相交于C、D两点; (2)作直线CD 老师说:“小芸的作法正确.” 请回答:小芸的作图依据是_________________________. 【考点】点、线 【难度】容易 【答案】到线段两个端点距离相等的点在线段的垂直平分线上;两个点确定一条直线。 【点评】本题考查线段的基本概念。 三.解答题 1. (2015山东济宁,19,8分)(本题满分8分) 如图,在△ABC中,AB=AC,∠DAC是△ABC的一个外角. 实践与操作: 根据要求尺规作图,并在图中标明相应字母(保留作图痕迹,不写作法). (1)作∠DAC的平分线AM; (2)作线段AC的垂直平分线,与AM交于点F,与BC边交于点E,连接AE、CF. 猜想并证明: 判断四边形AECF的形状并加以证明. 【答案】 试题解析:(1) (2)猜想:四边形AECF是菱形 证明:∵AB=AC ,AM平分∠CAD ∴∠B=∠ACB,∠CAD=2∠CAM ∵∠CAD是△ABC的外角 ∴∠CAD=∠B+∠ACB ∴∠CAD=2∠ACB ∴∠CAM=∠ACB ∴AF∥CE ∵EF垂直平分AC ∴OA=OC, ∠AOF=∠COE= ∴AOF≌△COE ∴AF=CE 在四边形AECF中,AF∥CE,AF=CE ∴四边形AECF是平行四边形 又∵EF⊥AC ∴四边形AECF是菱形 考点:角平分线,线段的垂直平分线的基本作图,等腰三角形的内外角,三角形全等,菱形的判定 2.(2015•广东省,第19题,6分)如图,已知锐角△ABC. (1)过点A作BC边的垂线MN,交BC于点D(用尺规作图法,保留作图痕迹,不要求写作法); 【答案】解:(1)作图如答图所示,AD为所作. 【考点】尺规作图(基本作图) 【分析】(1)①以点A为圆心画弧交BC于点E、F; ②分别以点E、F为圆心,大于长为半径画弧,两交于点G; ③连接AG,即为BC边的垂线MN,交BC于点D. 3. (2015•浙江杭州,第21题10分) “综合与实践”学习活动准备制作一组三角形,记这些三角形的三边分别为a,b,c,并且这些三角形三边的长度为大于1且小于5的整数个单位长度 (1)用记号(a,b,c)(a≤b≤c)表示一个满足条件的三角形,如(2,3,3)表示边长分别为2,3,3个单位长度的一个三角形,请列举出所有满足条件的三角形 (2)用直尺和圆规作出三边满足a查看更多
相关文章
- 当前文档收益归属上传用户