2020中考数学复习 第17课时 二次函数的综合应用（无答案）

2020中考数学复习 第17课时 二次函数的综合应用（无答案）

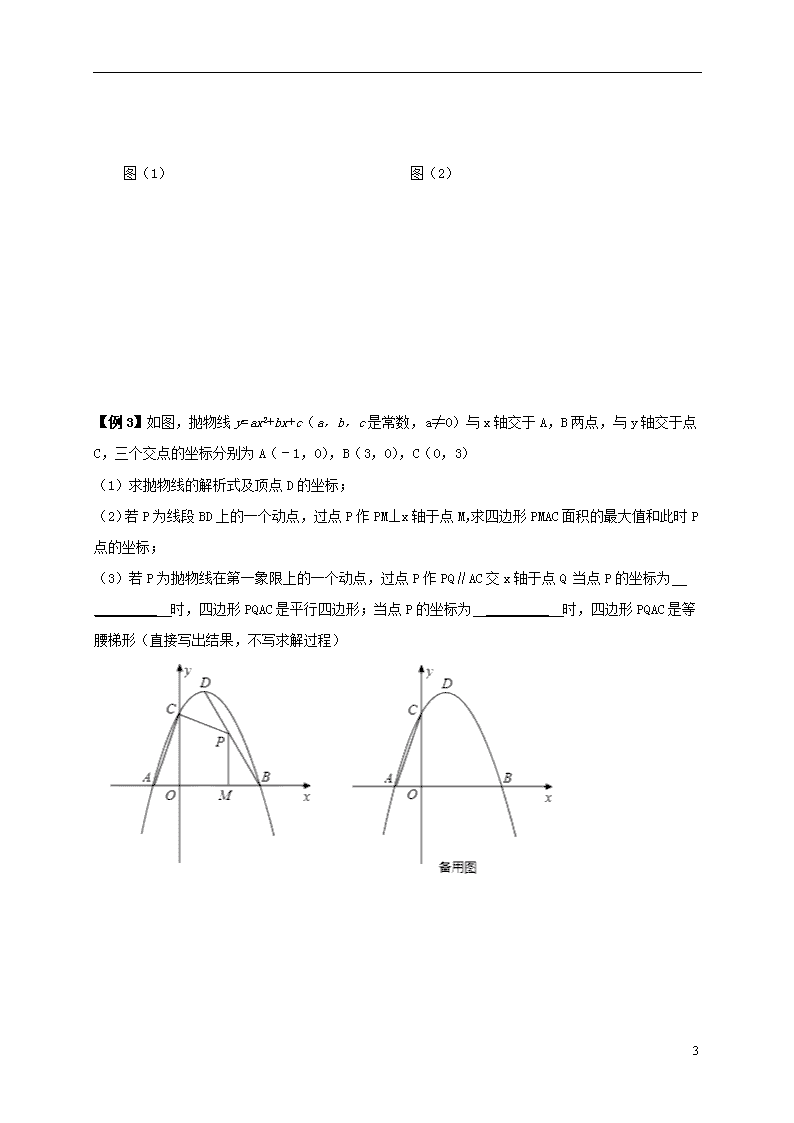
第17课时 二次函数的综合应用 ‎【课前展练】‎ ‎1（孝感2009）．对于每个非零自然数，抛物线与轴交于、两点，以表示这两点间的距离，则…的值是（ ）‎ A． B． C． D．‎ ‎2.（孝感2011）已知二次函数y=ax2+bx+c的图象如图所示，它与x轴的两个交点分别为（﹣1，0），（3，0）．对于下列命题：①b﹣‎2a=0；②abc＜0；③a﹣2b+‎4c＜0；④‎8a+c＞0．其中正确的有【 】‎ A．3个 B．2个 C．1个 D．0个 ‎3. 二次函数y＝ax2＋bx＋c(a≠0)的图象的对称轴是直线x＝1，其图象的一部分如图所示．下列说法正确的是 ▲ (填正确结论的序号)．‎ ‎①abc＜0；②a－b＋c＜0；③‎3a＋c＜0；④当－1＜x＜3时，y＞0．‎ ‎4. 对于二次函数y=x2-2mx-3，有下列说法：‎ ‎①它的图象与x轴有两个公共点；‎ ‎②如果当x≤1时y随x的增大而减小，则m=1；‎ ‎③如果将它的图象向左平移3个单位后过原点，则m=-1；‎ ‎④如果当x=4时的函数值与x=2008时的函数值相等，则当x=2012时的函数值为-3．‎ 其中正确的说法是 ___ ．（把你认为正确说法的序号都填上）‎ ‎【典型例题】‎ A C B D E O x y ‎2‎ ‎【例1】(孝感2010，12分)如图，已知二次函数的图象顶点坐标为(2，0)，直线y＝x＋1与二次函数的图象交于A、B两点，其中点A在y轴上．‎ ‎(1)二次函数的解析式为y＝ ．‎ ‎(2)证明点(―m，‎2m―1)不在(1)中所求的二次函数的图象上．‎ 3‎ ‎(3)C为线段AB的中点，过点C作CE⊥x轴于点E，CE与二次函数的图象交于点D．‎ ‎①y轴上存在点K，使以K、A、D、C为顶点的四边形是平行四边形，则点K的坐标是 ；‎ ‎②二次函数的图象上是否存在点P，使得S△POE＝2S△ABD？若存在，求出点P的坐标；若不存在，请说明理由．‎ ‎【例2】‎ 如图（1），矩形ABCD的一边BC在直角坐标系中x轴上，折叠边AD，使点D落在x轴上点F处，折痕为AE，已知AB=8，AD=10，并设点B坐标为（m，0），其中m＞0。‎ ‎（1）求点E、F的坐标（用含m的式子表示）； （2）连接OA，若△OAF是等腰三角形，求m的值； （3）如图（2），设抛物线y=a（x-m-6）2+h经过A、E两点，其顶点为M，连接AM，若∠OAM=90°，求a、h、m的值。‎ ‎（5分）‎ 3‎ ‎ ‎ 图（1） 图（2）‎ ‎ ‎ ‎【例3】如图，抛物线y=ax2+bx+c（a，b，c是常数，a≠0）与x轴交于A，B两点，与y轴交于点C，三个交点的坐标分别为A（﹣1，0），B（3，0），C（0，3） ‎ ‎（1）求抛物线的解析式及顶点D的坐标；‎ ‎（2）若P为线段BD上的一个动点，过点P作PM⊥x轴于点M，求四边形PMAC面积的最大值和此时P点的坐标；‎ ‎（3）若P为抛物线在第一象限上的一个动点，过点P作PQ∥AC交x轴于点Q 当点P的坐标为　_________　时，四边形PQAC是平行四边形；当点P的坐标为　_________　时，四边形PQAC是等腰梯形（直接写出结果，不写求解过程） ‎ 3‎