2018有关中考压轴题6

2018有关中考压轴题6

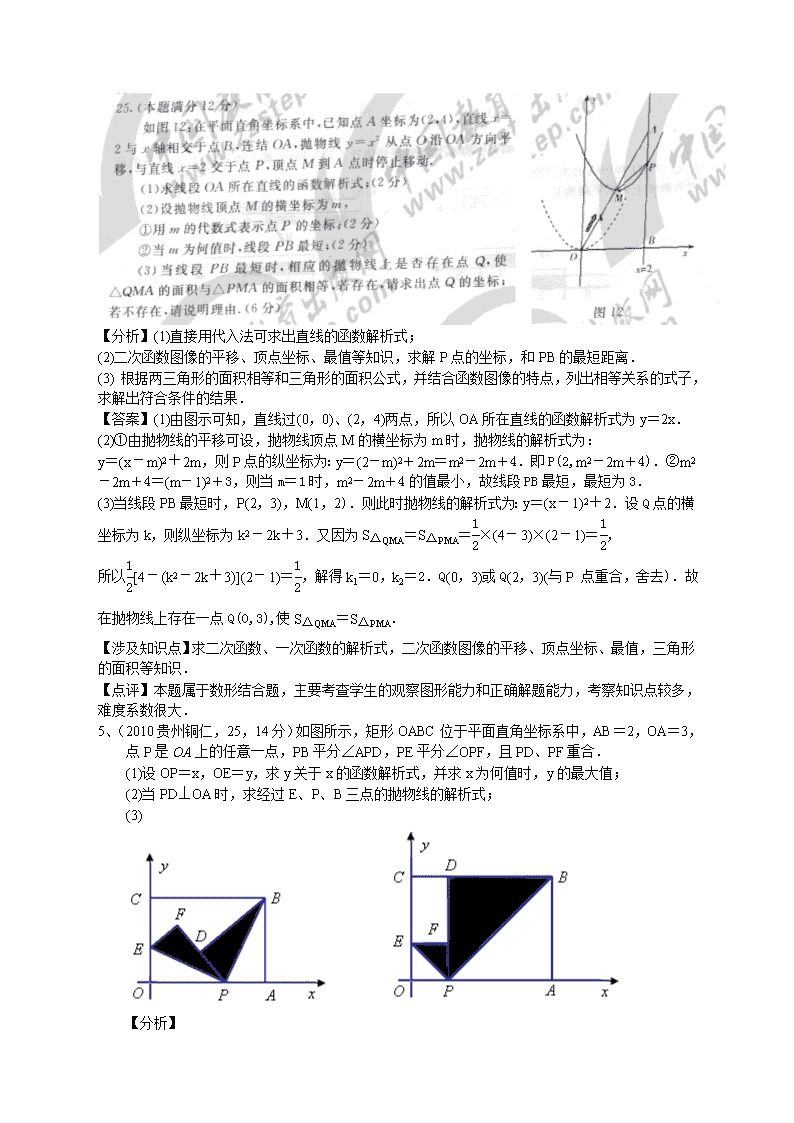
‎1、（2010 贵州安顺本题满分12分）‎ 已知：如图，抛物线与轴交点A、点B，与直线相交于点B、点 C，直线与轴交于点E．‎ ‎（1）写出直线BC的解析式．‎ ‎（2）求△ABC的面积．‎ ‎（3）若点M在线段AB上以每秒1个单位长度的速度从A向B运动（不与A，B重合），同时，点N在射线BC上以每秒2个单位长度的速度从B向C运动．设运动时间为秒，请写出△ABC的面积S与t的函数关系式，并求出点M运动多少时间时，△MNB的面积最大，最大面积是多少？‎ ‎【分析】由抛物线可以求出A、B坐标，从而求出直线BC 的解析式和C点坐标。易求△ABC的面积。利用MB,BN用t表示，求出三角形MBN的面积表达式，是个二次函数，根据二次函数的最值，求出△MNB的最大值。‎ ‎【答案】（1）由抛物线可以求出A（-2，0），B（2，0），直线BC: ‎ ‎ (2)解得：C（ -1，）.‎ 则S△ABC=‎ ‎(3)‎ ‎ ∵S=‎ 所以，当t=2时，S有最大值 ‎ 【涉及知识点】二次函数，动态变化，一次函数，三角形的面积表示，‎ ‎【点评】本题综合考查了，一次函数，二次函数，一元二次方程组，三角形的面积，二次函数的最值，同时，以运动变化的数学思想考查了学生的综合分析和数形结合的能力。‎ ‎2、（2010贵州毕节，25，12分）某同学用两个完全相同且有一个角为60°的直角三角尺重叠在一起（如图①），固定△ABC不动，将△DEF沿线段AB向右平移，当D移至AB中点时（如图②）‎ ‎（1）、求证：△ACD≌△DFB.‎ ‎ (2)、猜想四边形CDBF的形状，并说明理由.‎ 图① 图②‎ ‎【分析】利用平移的性质得到DF=AC，∠FDB=∠A，再由D是AB中点得DB=AD.这样可以利用SAS证明△ACD≌△DFB.利用平移的性质可以得CF=AD=DB，再根据直角三角形斜边上的中线等于斜边的一半得BF=CD=DB，从而得CF=CD=DB=BF，所以四边形CDBF是菱形.‎ ‎【答案】（1）∵D是AB中点，∴AD=DB,又根据平移性质得AC = DF，∠A=∠FDB，∴△ACD≌△DFB（SAS）.（2）∵D是AB中点，∠ACB=90°, ∴AD=DB=CD，同理，BF=DB, ∴AD=DB=CD=BF，∴四边形CDBF是菱形.‎ ‎【涉及知识点】平移、直角三角形的性质、菱形的判定方法.‎ ‎【点评】本题涉及图形变换与三角形、四边形等知识的综合应用，对学生解题能力的考查比较全面．‎ ‎3、（2010贵阳，25，12分）如图12，在直角坐标系中，已知点的坐标为（1,0），将线段绕原点O沿逆时针方向旋转45，再将其延长到，使得，得到线段；又将线段绕原点O沿逆时针方向旋转45，再将其延长到，使得，得到线段，如此下去，得到线段，，…，．‎ ‎（1）写出点M5的坐标；（4分）‎ ‎（2）求的周长；（4分）‎ ‎（3）我们规定：把点（0,1,2,3…）‎ 的横坐标，纵坐标都取绝对值后得到的新坐标 称之为点的“绝对坐标”．根据图中点 的分布规律，请你猜想点的“绝对坐标”，并写出来 ‎【分析】利用旋转的性质.‎ ‎【答案】（1）M5（―4，―4）；‎ ‎（2）由规律可知，,，， ∴的周长是.‎ ‎（3）解法一：由题意知，旋转8次之后回到轴的正半轴，在这8次旋转中，点分别落在坐标象限的分角线上或轴或轴上，但各点“绝对坐标”的横、纵坐标均为非负数，因此，点的“绝对坐标”可分三类情况：‎ 令旋转次数为，‎ ① 当点M在x轴上时: M0（），M4（），M8（），M12（）,…，‎ 即：点的“绝对坐标”为（）。当点M在y轴上时: M2，M6，M10，M14,即：点的“绝对坐标”为。当点M在各象限的分角线上时：M1，M3，M5，M7,即：的“绝对坐标”为。‎ 解法二：由题意知，旋转8次之后回到轴的正半轴，在这8次旋转中，点分别落在坐标象限的分角线上或轴或轴上，但各点“绝对坐标”的横、纵坐标均为非负数，因此，各点的“绝对坐标”可分三种情况：‎ ‎①当时（其中=0，1，2，3，…），点在轴上，则（）；‎ ‎②当时（其中=1，2，3，…），点在轴上，点（）；‎ ‎③当=1，2，3，…，时，点在各象限的分角线上，则点（）‎ ‎ 【涉及知识点】旋转、坐标 ‎【点评】旋转相关问题，通常都通过旋转的性质来加以解决。‎ ‎4、‎ ‎【分析】(1)直接用代入法可求出直线的函数解析式；‎ ‎(2)二次函数图像的平移、顶点坐标、最值等知识，求解P点的坐标，和PB的最短距离．‎ ‎(3) 根据两三角形的面积相等和三角形的面积公式，并结合函数图像的特点，列出相等关系的式子，求解出符合条件的结果．‎ ‎【答案】(1)由图示可知，直线过(0，0)、(2，4)两点，所以OA所在直线的函数解析式为y＝2x．‎ ‎(2)①由抛物线的平移可设，抛物线顶点M的横坐标为m时，抛物线的解析式为：‎ y＝(x－m)2＋2m，则P点的纵坐标为：y＝(2－m)2＋2m＝m2－2m＋4．即P(2,m2－2m＋4)．②m2－2m＋4＝(m－1)2＋3，则当m＝1时，m2－2m＋4的值最小，故线段PB最短，最短为3．‎ ‎(3)当线段PB最短时，P(2，3)，M(1，2)．则此时抛物线的解析式为：y＝(x－1)2＋2．设Q点的横坐标为k，则纵坐标为k2－2k＋3．又因为S△QMA＝S△PMA＝×(4－3)×(2－1)＝，‎ 所以[4－(k2－2k＋3)](2－1)＝，解得k1＝0，k2＝2．Q(0，3)或Q(2，3)(与P 点重合，舍去)．故在抛物线上存在一点Q(0,3),使S△QMA＝S△PMA．‎ ‎【涉及知识点】求二次函数、一次函数的解析式，二次函数图像的平移、顶点坐标、最值，三角形的面积等知识．‎ ‎【点评】本题属于数形结合题，主要考查学生的观察图形能力和正确解题能力，考察知识点较多，难度系数很大．‎ ‎5、（2010贵州铜仁，25，14分）如图所示，矩形OABC位于平面直角坐标系中，AB＝2，OA＝3，点P是OA上的任意一点，PB平分∠APD，PE平分∠OPF，且PD、PF重合．‎ ‎(1)设OP＝x，OE＝y，求y关于x的函数解析式，并求x为何值时，y的最大值；‎ ‎(2)当PD⊥OA时，求经过E、P、B三点的抛物线的解析式；‎ ‎(3)‎ ‎ ‎ ‎【分析】‎ ‎【答案】解：（1）由已知PB平分∠APD，PE平分∠OPF，且PD、PF重合，则∠BPE＝90°.‎ ‎∴∠OPE＋∠APB＝90°.又∠APB＋∠ABP＝90°，∴∠OPE＝∠PBA.‎ ‎∴Rt△POE∽Rt△BPA.‎ ‎∴.即.∴y＝x(3－x)＝－x2＋x(0

查看更多