- 2021-05-10 发布 |
- 37.5 KB |
- 10页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
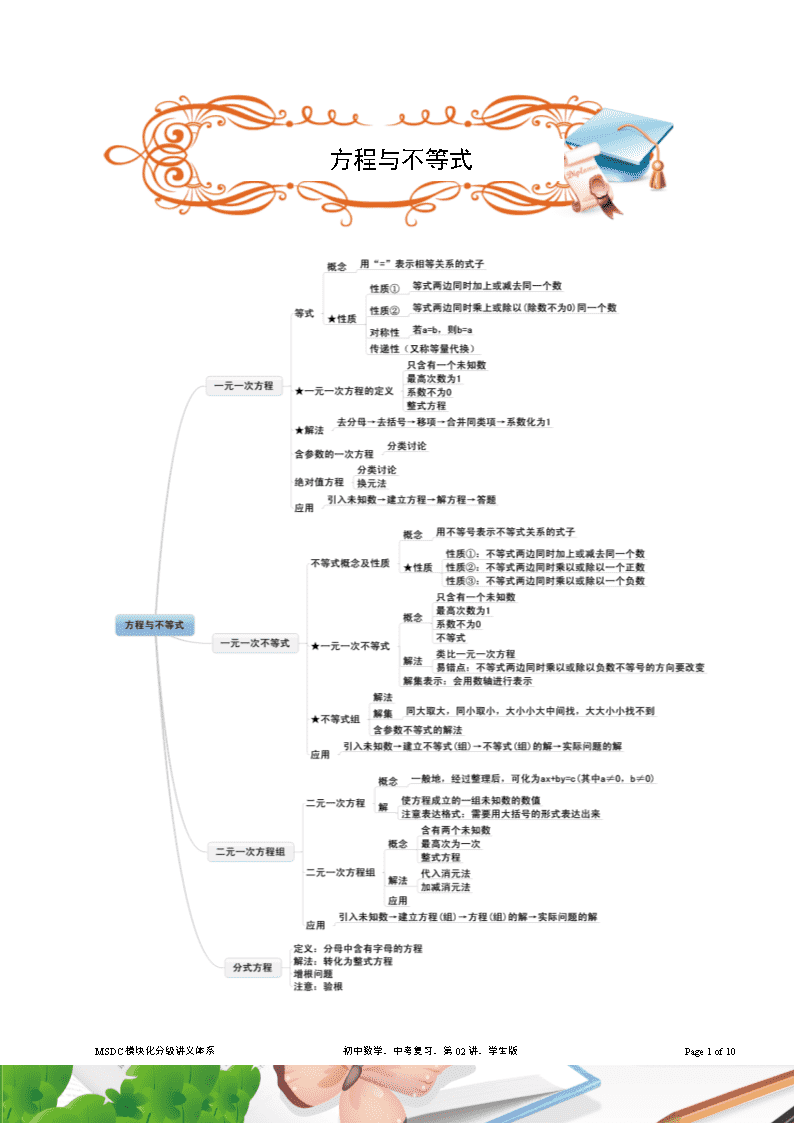
初中数学中考复习学生
方程与不等式 MSDC模块化分级讲义体系 初中数学.中考复习.第02讲.学生版 Page 10 of 10 考点汇总 考点一:等式的基本性质 考点二:不等式的基本性质 考点三:方程的概念(一元一次方程,二元一次方程) 考点四:方程的解(一元一次方程,二元一次方程,分式方程) 考点五:解方程(一元一次方程,二元一次方程,分式方程) 考点六:不等式的解集 考点七:解不等式 考点八:含参数方程 考点九:含参数不等式 考点十:绝对值方程 考点十一:实际应用题 MSDC模块化分级讲义体系 初中数学.中考复习.第02讲.学生版 Page 10 of 10 考点精讲 考点一:等式的基本性质 【例1】 若,那么下列各式成立的是( ) A. B. C. D. 【例2】 运用等式的性质对等式进行的变形中,正确的是( ) A.若,则 B.若,则 C.若,则 D.若,则 【例3】 若,则下列结论正确的是( ) A. B. C. D. 考点二:不等式的基本性质 【例4】 若,则下列各式不正确的是( ) A. B. C. D. 【例5】 如果关于的不等式的解集为,那么的取值范围是( ) A. B. C. D. 【例6】 若,那么下列各式成立的是( ) A. B. C. D. 考点三:方程的概念(一元一次方程,二元一次方程) 【例7】 已知下列方程①,②,③,④,⑤,⑥,其中是一元一次方程的个数是( ) A. B. C. D. 【例8】 已知是一元一次方程,则的值为_________ 【例9】 下列方程①,②,③,④,⑤中,是二元一次方程的个数为( ) A. B. C. D. MSDC模块化分级讲义体系 初中数学.中考复习.第02讲.学生版 Page 10 of 10 【例1】 已知方程是关于、的二元一次方程,则、需要满足的条件为_______ 考点四:方程的解(一元一次方程,二元一次方程,分式方程) 【例2】 不是哪一个方程的解( ) A. B. C. D. 【例3】 若是方程的解,则也是方程( )的解 A. B. C. D. 【例4】 已知是方程的解,则 【例5】 二元一次方程有无数多个解,下列四组值中不是该方程的解的是( ) A. B. C. D. 【例6】 方程组的解是( ) A. B. C. D. 【例7】 方程的解是( ) A. B.2 C.1 D.0 【例8】 分式方程的解是( ) A. B. C. D.无解 【例9】 分式方程有增根,则的值为 . 考点五:解方程(一元一次方程,二元一次方程,分式方程) 【例10】 解方程: MSDC模块化分级讲义体系 初中数学.中考复习.第02讲.学生版 Page 10 of 10 【例1】 用加减消元法解方程组 【例2】 用代入消元法解方程组 【例3】 解方程组: 【例4】 已知、满足方程组,则的值为_________. 【例5】 解分式方程 【例6】 解分式方程: MSDC模块化分级讲义体系 初中数学.中考复习.第02讲.学生版 Page 10 of 10 考点六:不等式的解集 【例1】 下列说法中错误的是( ) A.不等式的解集是 B.是不等式的一个解 C.不等式的整数解有无数多个 D.不等式的正整数解有无限个 【例2】 在数轴上表示的解集正确的是( ) 【例3】 不等式的负整数解为_____________ 考点七:解不等式 【例4】 解不等式组 【例5】 不等式组的所有整数解之和是( ) A.9 B.12 C.13 D.15 【例6】 不等式的非负整数解有( ) A.1个 B.2个 C.3个 D.4个 【例7】 不等式组的解集在数轴上表示正确的是( ) 【例8】 解不等式: MSDC模块化分级讲义体系 初中数学.中考复习.第02讲.学生版 Page 10 of 10 考点八:含参数方程 【例1】 若关于的方程的解为正整数,则整数的值为 . 【例2】 若和是关于的同解方程,则的值是 . 【例3】 解关于的方程: 【例4】 在方程组中,若未知数、满足,则的取值范围为( ) A. B. C. D. 【例5】 已知方程组与有相同的解,求、的值 【例6】 若方程有增根,则的值为( ) A. B. C.或 D.或 【例7】 若方程,那么、的值为( ) A., B., C. , D., 【例8】 已知关于x的分式方程-=0无解,则a的值为 . 【例9】 已知关于的方程有一个正数解,则的取值范围是___________ MSDC模块化分级讲义体系 初中数学.中考复习.第02讲.学生版 Page 10 of 10 考点九:含参数不等式 【例1】 若不等式的解都能使关于的一次不等式成立,则的取值范围是( ) A.1<≤7 B.≤7 C.<1或≥7 D.=7 【例2】 如果不等式组的解集是,那么的取值范围是( ) A. B. C. D. 【例3】 已知是关于的不等式的解,则的取值范围是_____________。 【例4】 已知关于的不等式的解集是,解不等式. 【例5】 已知不等式组 ⑴若它的解集是,求的取值范围。 ⑵若,且上述不等式无解,求的取值范围。 考点十:绝对值方程 【例6】 解方程 MSDC模块化分级讲义体系 初中数学.中考复习.第02讲.学生版 Page 10 of 10 【例1】 解方程 考点十一:实际应用题 【例2】 把一些笔记本分给几个学生,如果每人分3本,那么余8本;如果前面的每个学生分5本,那么最后一人就分不到3本.则共有学生 A.4人 B.5人 C.6人 D.5人或6人 【例3】 某校志愿者团队在重阳节购买了一批牛奶到“夕阳红”敬老院慰问孤寡老人,如果给每个老人分5盒,则剩下38盒,如果给每个老人分6盒,则最后一个老人不足5盒,但至少分得一盒. (1)设敬老院有名老人,则这批牛奶共有多少盒?(用含的代数式表示). (2)该敬老院至少有多少名老人?最多有多少名老人? 【例4】 随着人们节能意识的增强,节能产品进入千家万户,今年1月小明家将天燃气热水器换成了太阳能热水器.去年12月份小明家的燃气费是96元,从今年1月份起天燃气价格每立方米上涨25%,小明家2月份的用气量比去年12月份少10立方米,2月份的燃气费是90元.问小明家2月份用气多少立方米. MSDC模块化分级讲义体系 初中数学.中考复习.第02讲.学生版 Page 10 of 10 【例1】 “五一”节日期间,某超市进行积分兑换活动,具体兑换方法见右表. 爸爸拿出自己的积分卡,对小华说:“这里积有8200 分,你去给咱家兑换礼品吧”.小华兑换了两种礼品,共10件,还剩下了200分,请问她兑换了哪两种礼品,各多少件? 积分兑换礼品表 兑换礼品 积分 电茶壶一个 7000分 保温杯一个 2000分 牙膏一支 500分 【例2】 2010年6月5日是第38个世界环境日,世界环境日的主题为“多个物种.一颗星球.一个未来”.为了响应节能减排的号召,某品牌汽车4S店准备购进A型(电动汽车)和B型(太阳能汽车)两种不同型号的汽车共16辆,以满足广大支持环保的购车者的需求.市场营销人员经过市场调查得到如下信息: 成本价(万元/辆) 售价(万元/辆) A型 30 32 B型 42 45 (1)若经营者的购买资金不少于576万元且不多于600万元,则有哪几种进车方案? (2)在(1)的前提下,如果你是经营者,并且所进的汽车能全部售出,你会选择哪种进车方案才能使获得的利润最大?最大利润是多少? (3)假设每台电动汽车每公里的用电费用为0.65元,且两种汽车最大行驶里程均为30万公里,那么从节约资金的角度,你做为一名购车者,将会选购哪一种型号的汽车?并说明理由. MSDC模块化分级讲义体系 初中数学.中考复习.第02讲.学生版 Page 10 of 10查看更多