- 2021-05-10 发布 |
- 37.5 KB |
- 14页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2020年中考数学专题复习:全等到相似的转化
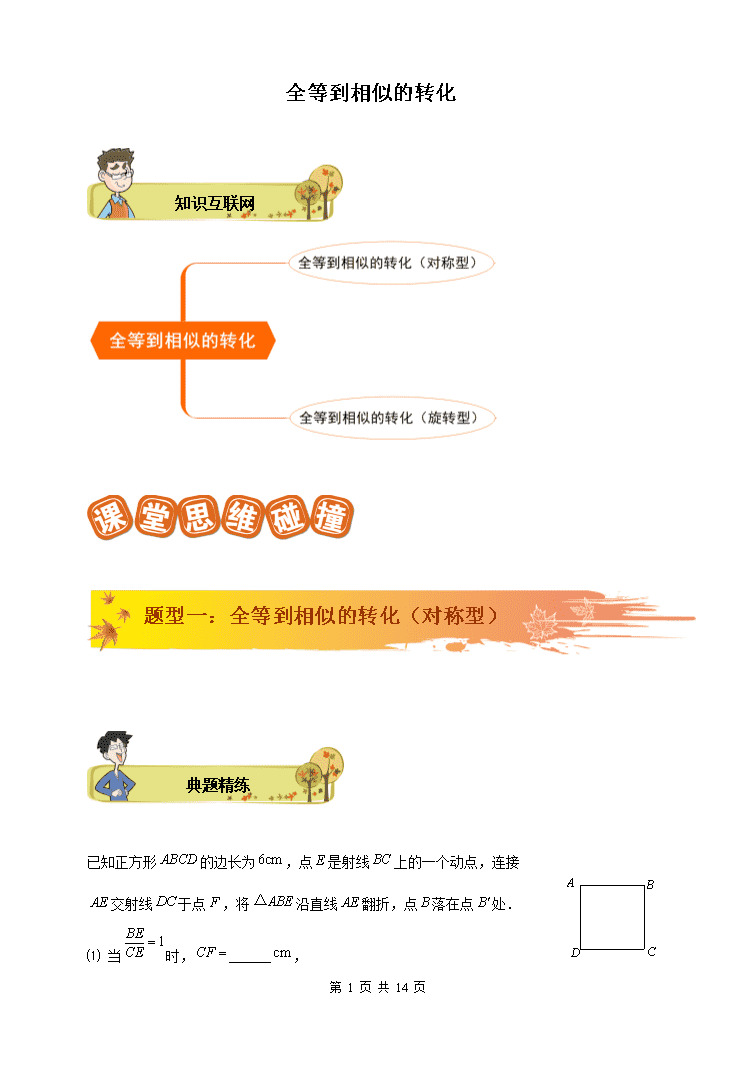
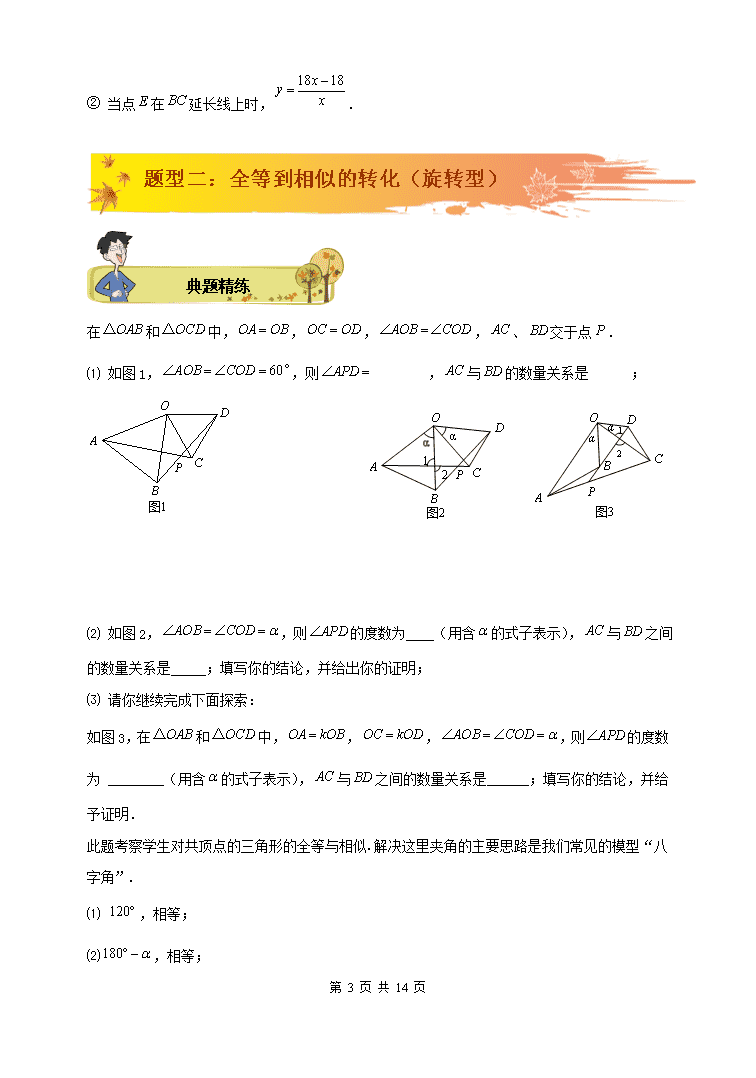
全等到相似的转化[中%国教*~育^出版网@] 知识互联网 [来源:~z*zs&tep.c#om^] [来&源~:*zzstep.co@m%] 题型一:全等到相似的转化(对称型) [来~#源%*:^中国教育出版网] 典题精练 已知正方形的边长为,点是射线上的一个动点,连接交射线于点,将沿直线翻折,点落在点处. ⑴ 当时,______,[w~ww.z#zs^te%p@.com] 第 13 页 共 14 页 ⑵ 当时,求的值; ⑶ 当时(点与点不重合),请写出翻折后与正方形公共部分的面积与的关系式,(只要写出结论,不要解题过程). ⑴ 6 ; ⑵ ① 如图1,当点在上时,延长交于点, ∵,∴,∴. ∵,∴. ∵,∴. 又,∴.∴.[w#ww.zzs%t*ep^.co@m] 设,则,.[来~源:zz*^ste%@p.com] 在中,由勾股定理得: ,解得.∴. ∴; ② 如图2,当点在延长线上时,延长交于点, 同①可得. 设,则. 在中,由勾股定理,得 ,解得.∴. ∴. ⑶ ① 当点在上时,;[来源&:中教网@*#^] (所求的面积即为的面积,再由相似表示出边长) 第 13 页 共 14 页 ② 当点在延长线上时,. [中国#&教育出*版网@~] 题型二:全等到相似的转化(旋转型) 典题精练 在和中,,,,、交于点. ⑴ 如图1,,则 ,与的数量关系是 ; [来源:zzs%t&ep~.#co@m] ⑵ 如图2,,则的度数为____(用含的式子表示),与之间的数量关系是_____;填写你的结论,并给出你的证明; ⑶ 请你继续完成下面探索: 如图3,在和中,,,,则的度数为 ________(用含的式子表示),与之间的数量关系是______;填写你的结论,并给予证明. 此题考察学生对共顶点的三角形的全等与相似.解决这里夹角的主要思路是我们常见的模型“八字角”. ⑴ ,相等; ⑵,相等;[中国教育出%版网^@*&] 第 13 页 共 14 页 ∵,∴[中~国&^教育出#*版网] ∴,∴, ∵,∴ ∵,∴,∴. ⑶ ,. 易证,∴, ∵,∴,∴,[来#^源:@中国教育出版~网*] ∴.[www&.z~z*st%ep.com#] [来源:^zzste~p.%com@&] 如图,直线与线段相交于点, 点和点在直线上,且. ⑴ 如图1所示,当点与点重合时 ,且,请写出与的数量关系和位置关系; ⑵ 将图1中的绕点顺时针旋转到如图2所示的位置,,⑴中的与的数量关系和位置关系是否仍然成立?若成立,请证明;若不成立,请说明理由; ⑶ 将图2中的拉长为的倍得到如图3,求的值. 【答案】⑴ ; 第 13 页 共 14 页 ⑵ 仍然成立. 证明: 过点作于,过点作于 ∴ ∵, ∴≌ ∴[来源:*中@教#&网~] ∵ ∴ ∴ 延长与的延长线相交点 ∴ 又∵ ∴ ∴ ⑶ 过点作于,过点作于 易证[来源:中&*国^教育出#版网@] ∴ . ∵ , ∴ . 由⑵知 . 第 13 页 共 14 页 . 如图,是由绕点顺时针旋转得到的,连结交斜边于点,的延长线交于点. ⑴ 证明:; ⑵ 设,,试探索、满足什么关系时,与是全等三角形,并说明理由. [ww&w^.zzstep*#.co@m] ⑴ 证明:∵是由绕点顺时针旋转得到的, ∴,,[www.#zzst&*e~p.c@om] ∴ ∴[来源:中@#国教*育出版~网^] 又 ∴ ⑵ 解:当时,[来~源*:中国教育出版^&@网] 在¢中,∵ ∴ 在中, ,即, ∴. ∵, ∴ 第 13 页 共 14 页 ∴ 由⑴知:, ∴.[中国教育&出^*@版网#] 如图,正方形的对角线与相交于点,正方形与正方形全等,射线与不过、、、四点且分别交BC.CD的边于、两点.[来#%&源*:@中教网] ⑴ 求证:; ⑵ 若将原题中的正方形改为矩形,且,其他条件不变,探索线段与[中国教育出%~*#版网^] 线段的数量关系.[w#ww.zz@s^tep%~.com] [www.z%#z&ste^p@.com] ⑴ 证明:过点作于点,于点. ∴. ∵为正方形对角线、的交点, ∴. 第 13 页 共 14 页 又∵ ∴ 在和中 [来源:中~^&国#教育出版网@] ∴. ∴. ⑵ 解:当交于点,交于点时. 过点作于点,于点H. ∴∠MGE=∠MHF=.[来源:@~&中#教网^] ∵M为矩形对角线AC.BD的交点, ∴∠EMG+∠GMQ =∠HMF +∠GMQ=. ∴∠EMG =∠HMF. 在△MGE和△MHF中, ∴△MGE∽△MHF. ∴. ∵M为矩形对角线AC.BD的交点,∴MB=MD=MC 又∵MG⊥BC,MH⊥CD,∴点G、H分别是BC.DC的中点. ∵, ∴. ∴.[来%~源:中教*^网&] 如图,是两个全等的等腰直角三角形,,的顶点 第 13 页 共 14 页 与的斜边的中点重合.将绕点旋转,旋转过程中,线段与线段相交于点,线段与射线相交于点. (1)如图①,当点在线段上,且时,求证:; (2)如图②,当点在线段的延长线上时,求证:;并求当,时,两点间的距离 (用含的代数式表示). 【解析】(1)证明:∵是等腰直角三角形, ∴, ∵, ∴, ∵的中点, ∴,[来&源:#中教^%网~] 在中, ∴ ∴; (2)解:连接, ∵是两个全等的等腰直角三角形, 第 13 页 共 14 页 ∴, ∵, 即, ∴, ∴, ∴, ∴, ∵,,, ∴, ∴, ∴, ∴, 在中,. 复习巩固 题型一 全等到相似的转化(对称型) 如右图,在正方形ABCD中,AB=1,BE⊥AP于E,DF⊥AP于F, 若= m(m为常数),则= . 如图,已知,,,以为边作矩形ABCD,使 第 13 页 共 14 页 ,过点D作DE垂直OA的延长线交于点E.[ww#w~.z%zst@ep^.com] O B C A E D ⑴ 当a为何值时,?请说明理由,并求此时点C到OE的距离. ⑵ 当a为何值时,C到OE的距离是15?[中国^*教育#&~出版网] ⑴ 当时, ∵,,∴,当时,,∵ ,∴ 过作,过作. ∵为矩形. 又∵,∴为正方形 ∴,,[中国^教@&育出版%网*] ∴,∴ ∴,∴ ⑵ 当时,到的距离是15; ∵,∴, ∴,∴, ∴,∴,∴ [中*国教%@育~出版^网] 第 13 页 共 14 页 题型二 全等到相似的转化(旋转型) 现有一副直角三角板,按下列要求摆放: ⑴ 如图1,固定等腰直角三角板,于,另一个直角三角板的直角顶点与重合,现让三角板绕点旋转,保证、分别交、于点、.试探求的值; ⑵ 如图2,交换两块三角板的位置,固定直角三角板,于,另一个等腰直角三角板的直角顶点与点重合,、分别交、于点,,试问的值又将如何变化? ⑴ ,,,得,.[来#%源:^~中教网&] ⑵由,得,又由,得,故. 如图1,在中,,,是边上一点,是边上 的一个动点(与点、不重合),,与射线相交于点. ⑴如图2,如果点是边的中点,求证:; ⑵如果,求的值. 第 13 页 共 14 页 ⑴ 如图,连结,那么是等腰直角三角形的斜边上的高. 根据“角边角”可以证明,从而得到. ⑵ 如图,作,,垂足分别为点、, 那么与都是等腰直角三角形,. 因为与都是的余角, 所以.[来源~%:zzs#t*ep.co&m] 又因为, 所以. 因此. 填空或解答:点B.C.E在同一直线上,点A.D在直线CE的同侧,,, ,直线AE.BD交于点F. ⑴ 如图1,若,则_________;如图2,若,则 _________; ⑵ 如图3,若,则_________(用含的式子表示); ⑶ 将图3中的△ABC绕点C旋转(点F不与点A.B重合),得图4或图5.在图4中, 与的数量关系是___________;在图5中,与的数量关系是___________.请你任选其中一个结论证明. 第 13 页 共 14 页 A A A B B B C C C D D D E E E F F F 图1 图2 图3 [中^国教#育出~版&*网] A A B B C C D D E E F F 图4 图5 Q ⑴ ,; ⑵ ;[来#源:~中国%教*育@出版网] ⑶ 图4中:; 图5中:. 的证明如下: 如图4,设与的交点为[中国教育%出版网@~#*] ∵,,. ∴, ∴,, ∴,得[来%@源&:^中~教网] ∵ ∴.[来&源@:~中教^#网] 第 13 页 共 14 页查看更多