中考数学专题复习4两线段之和最短

中考数学专题复习4两线段之和最短

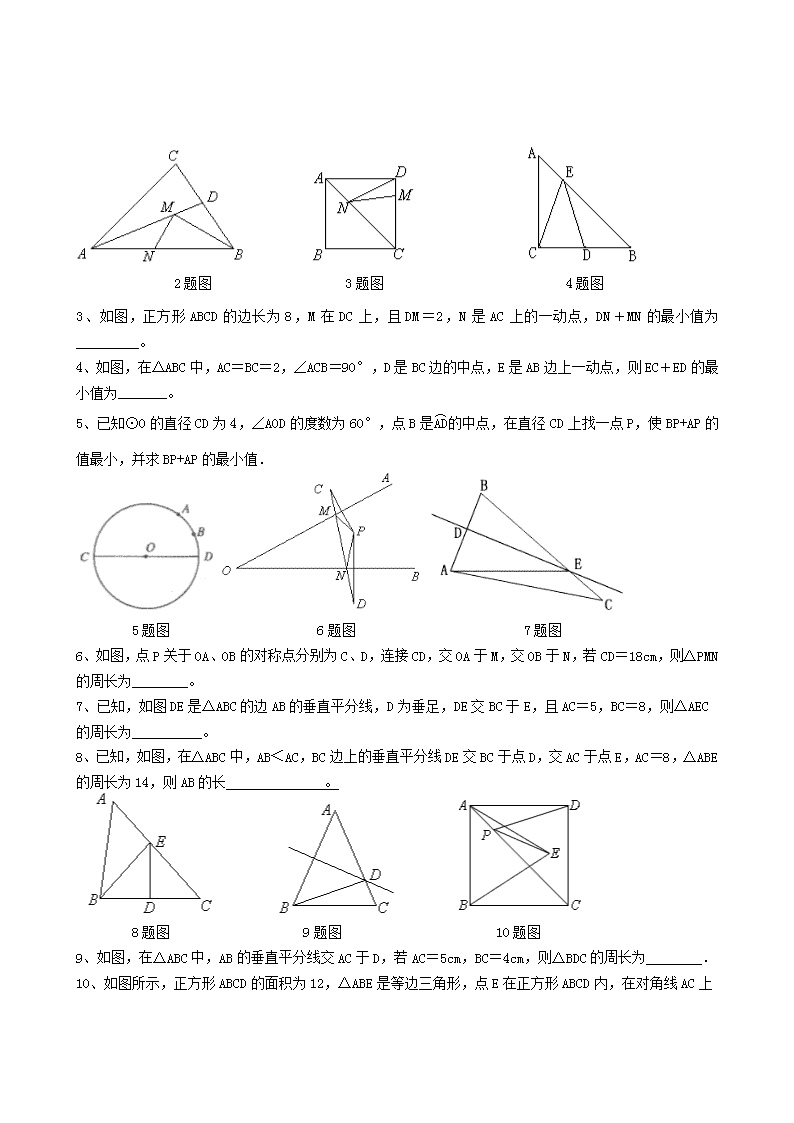
‎2011年中考复习（4）——两线段之和最短专题 一、数学模型 ‎1、实际问题：‎ 如图，要在河边修建一个水泵站，分别向张村、李庄送水，修在河边什么地方可使所用的水管最短 ‎2、数学问题：‎ 已知：直线l和l的同侧两点A、B。‎ 求作：点C，使C在直线l上，并且AC＋CB最小。‎ 二、构建“对称模型”实现转化 三、练习题 ‎（一）填空题 ‎1、（2009年孝感）在平面直角坐标系中，有A（3，－2），B（4，2）两点，现另取一点C（1，n），当n =______时，AC + BC的值最小．‎ ‎2、（2009陕西）如图，在锐角△ABC中，AB＝4，∠BAC＝45°，∠BAC的平分线交BC于点D，M、N分别是AD和AB上的动点，则BM+MN的最小值是____．‎ ‎ ‎ ‎2题图 3题图 4题图 ‎3、如图，正方形ABCD的边长为8，M在DC上，且DM＝2，N是AC上的一动点，DN＋MN的最小值为_________。‎ ‎4、如图，在△ABC中，AC＝BC＝2，∠ACB＝90°，D是BC边的中点，E是AB边上一动点，则EC＋ED的最小值为_______。‎ ‎5、已知⊙O的直径CD为4，∠AOD的度数为60°，点B是的中点，在直径CD上找一点P，使BP+AP的值最小，并求BP+AP的最小值．‎ ‎5题图 6题图 7题图 ‎6、如图，点P关于OA、OB的对称点分别为C、D，连接CD，交OA于M，交OB于N，若CD＝‎18cm，则△PMN的周长为________。‎ ‎7、已知，如图DE是△ABC的边AB的垂直平分线，D为垂足，DE交BC于E，且AC＝5，BC＝8，则△AEC的周长为__________。‎ ‎8、已知，如图，在△ABC中，AB＜AC，BC边上的垂直平分线DE交BC于点D，交AC于点E，AC＝8，△ABE的周长为14，则AB的长 。‎ ‎ ‎ ‎8题图 9题图 10题图 ‎9、如图，在△ABC中，AB的垂直平分线交AC于D，若AC＝‎5cm，BC＝‎4cm，则△BDC的周长为________．‎ ‎10、如图所示，正方形ABCD的面积为12，△ABE是等边三角形，点E在正方形ABCD内，在对角线AC 上有一点P，使PD＋PE的和最小，则这个最小值为（ ）‎ A．2 B．‎2‎ C．3 D． ‎10、（1）如图1，等腰Rt△ABC的直角边长为2，E是斜边AB的中点，P是AC边上的一动点，则PB+PE的最小值为 ；‎ ‎（2）几何拓展：如图2，△ABC中，AB=2，∠BAC=30°，若在AC、AB上各取一点M、N，使BM+MN的值最小，则这个最小值 ‎ ‎（二）作图题 ‎1、如图，一辆汽车在直线形的公路AB上由A向B行驶，M、N分别是位于公路AB两侧的村庄。‎ ‎（1）设汽车行驶到公路AB上点P位置时，距离村庄M最近；行驶到点Q位置时，距离村庄N最近。请在图中的AB上分别画出点P、Q的位置；‎ ‎（2）当汽车从A出发向B行驶时，在公路AB的哪一段路上距离M、N两村庄都越来越近？在哪一段路上距离村庄N越来越近，而离村庄M却越来越远？‎ ‎（3）在公路AB上是否存在这样一点H，使汽车行驶到该点时，与村庄M、N的距离相等？如果存在，请在图中的AB上画出这一点；如果不存在，请简要说明理由。‎ 2、 如图，村庄A、B位于一条小河的两侧，若河岸a、b彼此平行，现在要建设一座与河岸垂直的桥CD，问桥址应如何选择，才能使A村到B村的路程最近？‎ ‎3、如图，A、B是直线a同侧的两定点，定长线段PQ在a上平行移动，问PQ移动到什么位置时，AP+PQ+QB的长最短？‎ 4、 如图，已知∠AOB内有一点P，试分别在边OA和OB上各找一点E、F，使得△PEF的周长最小。试画出图形，并说明理由。‎ ‎（三）解答题 ‎1、如图，A、B两个小集镇在河流CD的同侧，分别到河的距离为AC＝‎10千米，BD＝‎30千米，且CD＝‎30千米，现在要在河边建一自来水厂，向A、B两镇供水，铺设水管的费用为每千米3万，请你在河流CD上选择水厂的位置M，使铺设水管的费用最节省，并求出总费用是多少？‎ ‎ ‎ ‎2、一次函数y=kx+b的图象与x、y轴分别交于点A（2，0），B（0，4）．‎ ‎（1）求该函数的解析式；‎ ‎（2）O为坐标原点，设OA、AB的中点分别为C、D，P为OB上一动点，求PC＋PD的最小值，并求取得最小值时P点坐标．‎ ‎3、如图，在平面直角坐标系中，直线l是第一、三象限的角平分线．‎ 实验与探究：‎ ‎（1）由图观察易知A（0，2）关于直线l的对称点A′的坐标为（2，0），请在图中分别标明B（5，3）、C（－2，5）关于直线l的对称点B′、C′的位置，并写出他们的坐标：B′ 、C′ ；‎ 归纳与发现：‎ ‎（2）结合图形观察以上三组点的坐标，你会发现：坐标平面内任一点P（a，b）关于第一、三象限的角平分线l的对称点P′的坐标为 （不必证明）；‎ 运用与拓广：‎ ‎（3）已知两点D（1，－3）、E（－1，－4），试在直线l上确定一点Q，使点Q到D、E两点的距离之和最小，并求出Q点坐标．‎