2019年中考数学提分训练 尺规作图（含解析） 新版新人教版

2019年中考数学提分训练 尺规作图（含解析） 新版新人教版

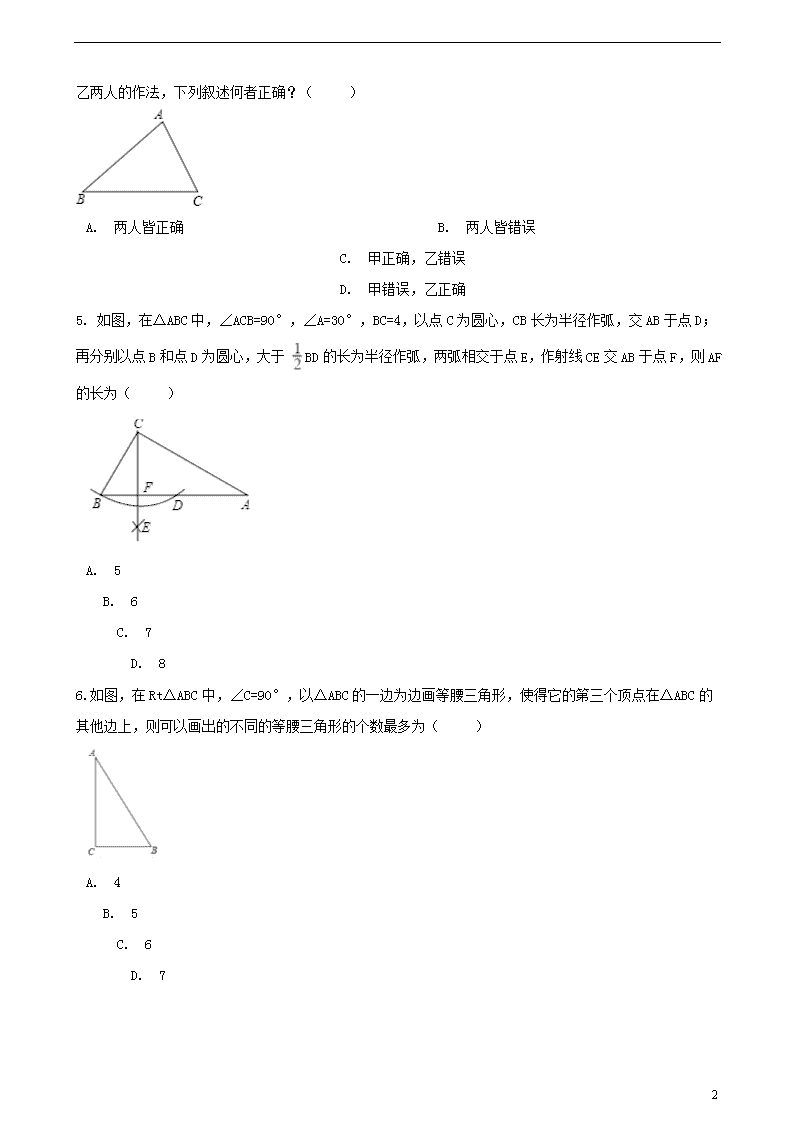
‎2019年中考数学提分训练: 尺规作图 一、选择题 ‎1.下列画图的语句中，正确的为（   ） ‎ A. 画直线AB=10cm B. 画射线OB=10cm C. 延长射线BA到C，使BA=BC D. 过直线AB外一点画一条直线和直线AB相交 ‎2.如图，用尺规作出了BF∥OA，作图痕迹中，弧MN是（   ） ‎ A. 以B为圆心，OD长为半径的弧                            B. 以C为圆心，CD长为半径的弧 C. 以E为圆心，DC长为半径的弧                             D. 以E为圆心，OD长为半径的弧 ‎3.用直尺和圆规作一个角等于已知角，如图，能得出 的依据是（   ）    ‎ A. （SAS）                            B. （SSS）                            C. （AAS）                            D. （A SA）‎ ‎4.如图，锐角三角形ABC中，BC＞AB＞AC，甲、乙两人想找一点P，使得∠BPC与∠A互补，其作法分别如下： （甲）以A为圆心，AC长为半径画弧交AB于P点，则P即为所求； （乙）作过B点且与AB垂直的直线l，作过C点且与AC垂直的直线，交l于P点，则P 23‎ 即为所求对于甲、乙两人的作法，下列叙述何者正确？（   ） ‎ A. 两人皆正确                  B. 两人皆错误                  C. 甲正确，乙错误                  D. 甲错误，乙正确 ‎5. 如图，在△ABC中，∠ACB=90°，∠A=30°，BC=4，以点C为圆心，CB长为半径作弧，交AB于点D；再分别以点B和点D为圆心，大于 BD的长为半径作弧，两弧相交于点E，作射线CE交AB于点F，则AF的长为（   ）‎ ‎ ‎ A. 5                                           B. 6                                           C. 7                                           D. 8‎ ‎6.如图，在Rt△ABC中，∠C=90°，以△ABC的一边为边画等腰三角形，使得它的第三个顶点在△ABC的其他边上，则可以画出的不同的等腰三角形的个数最多为（   ） ‎ A. 4                                           B. 5                                           ‎ 23‎ C. 6                                           D. 7‎ ‎7.画正三角形ABC（如图）水平放置的直观图△A′B′C′，正确的是（   ） ‎ A.            B.            C.            D. ‎ ‎8.已知∠AOB，用尺规作一个角 等于已知角∠AOB的作图痕迹如图所示，则判断∠AOB= 所用到的三角形全等的判断方法是（    ） ‎ A. SAS                                     B. ASA                                     C. AAS                                     D. SSS ‎9.如图，在△ABC中，∠C=90°，∠B=30°，以点A为圆心，任意长为半径画弧分别交AB，AC于点M和N，再分别以点M，N为圆心画弧，两弧交于点P，连结AP并延长交BC于点D，则下列说法中正确的个数是（    ） ①AD是∠BAC的平分线②∠ADC=60°③△ABD是等腰三角④点D到直线AB的距离等于CD的长度． ‎ A. 1                                           ‎ 23‎ B. 2                                           C. 3                                           D. 4‎ ‎10. 如图，用尺规作图作∠AOC=∠AOB的第一步是以点O为圆心，以任意长为半径画弧①，分别交OA、OB于点E、F，那么第二步的作图痕迹②的作法是（   ）‎ ‎ ‎ A. 以点F为圆心，OE长为半径画弧                          B. 以点F为圆心，EF长为半径画弧 C. 以点E为圆心，OE长为半径画弧                          D. 以点E为圆心，EF长为半径画弧 ‎11. 如图，在▱ABCD中，用直尺和圆规作∠BAD的平分线AG，若AD=5，DE=6，则AG的长是（   ） ‎ A. 6                                          B. 8                                          C. 10                                          D. 12‎ ‎12. 如图，在▱ABCD中，用直尺和圆规作∠BAD的平分线AG交BC于点E．若BF=8，AB=5，则AE的长为（   ）‎ ‎ ‎ 23‎ A. 5                                           B. 6                                           C. 8                                           D. 12‎ 二、填空题 ‎ ‎13. 我们学过用直尺和三角尺画平行线的方法，如图所示，直线a∥b的根据是________． ‎ ‎14.作图并写出结论：如图，点P是∠AOB的边OA上一点，请过点P画出OA , OB的垂线，分别交BO 的延长线于M 、N ,线段________的长表示点P到直线BO的距离；线段________的长表示点M到直线AO的距离 ; 线段ON的长表示点O到直线________的距离；点P到直线OA的距离为________. ‎ ‎15.如图，已知线段AB，分别以点A，B为圆心，大于线段AB长度一半的长为半径画弧，相交于点C，D，连接AC，BC，BD，CD．其中AB=4，CD=5，则四边形ABCD的面积为________．‎ ‎ ‎ ‎16.如图，在Rt△ABC中，∠ACB=90°，BC=9，AC=12．分别以点A和点B为圆心、大于AB一半的长为半径作圆弧，两弧相交于点E和点F，作直线EF交AB于点D，连结CD．则CD的长为________． ‎ 23‎ ‎17. 如图，依据尺规作图的痕迹，计算∠α=________°．‎ ‎ ‎ ‎18. 以Rt△ABC的锐角顶点A为圆心，适当长为半径作弧，与边AB，AC各相交于一点，再分别以这两个交点为圆心，适当长为半径作弧，过两弧的交点与点A作直线，与边BC交于点D.若∠ADB=60°，点D到AC的距离为2，则AB的长为________. ‎ ‎19.如图，在每个小正方形的边长为1的网格中，点A，B均在格点上． （Ⅰ）线段AB的长为________． （Ⅱ）请利用网格，用无刻度的直尺在AB上作出点P，使AP= ，并简要说明你的作图方法（不要求证明）．________． ‎ ‎20.如图，在矩形 中，按以下步骤作图：①分别以点 和 为圆心，以大于 的长为半径作弧，两弧相交于点 和 ；②作直线 交 于点 .若 ， ，则矩形的对角线 的长为________．‎ 三、解答题 ‎ 23‎ ‎21.如图，利用尺规，在△ABC的边AC上方作∠CAE=∠ACB，在射线AE上截取AD=BC，连接CD，并证明：CD∥AB（尺规作图要求保留作图痕迹，不写作法） ‎ ‎22.已知：如图，Rt△ABC中，∠ACB=90°‎ ‎（1）用直尺和圆规作∠ABC的平分线，交AC于点O； ‎ ‎（2）在（1）的条件下，若BC=3，AC=4，求点O到AB的距离。 ‎ ‎23.如图，在 中， . ‎ ‎（1）作 的平分线交 边于点 ，再以点 为圆心， 的长为半径作 ；（要求：不写作法，保留作图痕迹） ‎ ‎（2）判断（1）中 与 的位置关系，直接写出结果. ‎ ‎24.如图，BD是菱形ABCD的对角线，∠CBD=75°， ‎ 23‎ ‎（1）请用尺规作图法，作AB的垂直平分线EF，垂足为E，交AD于F；（不要求写作法，保留作图痕迹） ‎ ‎（2）在（1）条件下，连接BF，求∠DBF的度数． ‎ ‎25.如图，在Rt△ABC中，∠BAC=90°，∠C=30°． ‎ ‎（1）请在图中用尺规作图的方法作出AC的垂直平分线交BC于点D，交AC于点E （不写作法，保留作图痕迹）． ‎ ‎（2）在（1）的条件下，连接AD，求证：△ABC∽△EDA． ‎ ‎26.如图，在四边形ABCD中，∠B=∠C=90°，AB＞CD，AD=AB+CD．‎ ‎（1）利用尺规作∠ADC的平分线DE，交BC于点E，连接AE（保留作图痕迹，不写作法） ‎ ‎（2）在（1）的条件下，①证明：AE⊥DE； ②若CD=2，AB=4，点M，N分别是AE，AB上的动点，求BM+MN的最小值。 ‎ 23‎ 答案解析 ‎ 一、选择题 ‎1.【答案】D ‎ ‎【解析】 ：A、错误．直线没有长度； B、错误．射线没有长度； C、错误．射线有无限延伸性，不需要延长； D、正确． 故答案为：D． 【分析】根据直线、射线、线段的性质即可一一判断；‎ ‎2.【答案】C ‎ ‎【解析】   ：弧MN是以E为圆心，DC长为半径的弧。 故答案为  ：C。【分析】根据平行线的判定，这里要使BF∥OA，其依据是内错角相等，两直线平行，故根据尺规作图就是作一个角∠FBO=∠AOB,故弧MN，是以E为圆心，DC长为半径的弧。‎ ‎3.【答案】B ‎ ‎【解析】 ：根据画法可知OD=OC=OD=OC DC=DC 在△ODC和△ODC中 ∴△ODC≌△ODC（SSS） ∴∠A′O′B′=∠AOB. 故答案为：B 【分析】根据画法可知△ODC和△ODC的三边相等，得出两三角形全等，再根据全等三角形的性质可得出结论。‎ ‎4.【答案】D ‎ ‎【解析】 ：甲：如图1， ‎ 23‎ ‎∵AC=AP， ∴∠APC=∠ACP， ∵∠BPC+∠APC=180° ∴∠BPC+∠ACP=180°， ∴甲错误； 乙：如图2， ∵AB⊥PB，AC⊥PC， ∴∠ABP=∠ACP=90°， ∴∠BPC+∠A=180°， ∴乙正确， 故答案为：D． 【分析】甲：根据等边对等角可得∠APC=∠ACP，再由平角的定义可得∠BPC+∠APC=180°,等量带环即可判断； 乙：根据四边形的内角和为， 可知乙的作法正确。‎ ‎5.【答案】B ‎ ‎【解析】 ：连接CD， ∵在△ABC中，∠ACB=90°，∠A=30°，BC=4， ∴AB=2BC=8． ∵作法可知BC=CD=4，CE是线段BD的垂直平分线， ∴CD是斜边AB的中线， ∴BD=AD=4， ∴BF=DF=2， ∴AF=AD+DF=4+2=6． 故选B． ‎ 23‎ ‎ 【分析】连接CD，根据在△ABC中，∠ACB=90°，∠A=30°，BC=4可知AB=2BC=8，再由作法可知BC=CD=4，CE是线段BD的垂直平分线，故CD是斜边AB的中线，据此可得出BD的长，进而可得出结论．‎ ‎6.【答案】D ‎ ‎【解析】 如图， ①以B为圆心，BC长为半径画弧，交AB于点D，△BCD就是等腰三角形； ②以A为圆心，AC长为半径画弧，交AB于点E，△ACE就是等腰三角形； ③以C为圆心，BC长为半径画弧，交AC于点F，△BCF就是等腰三角形； ④作AC的垂直平分线交AB于点H，△ACH就是等腰三角形； ⑤作AB的垂直平分线交AC于G，则△AGB是等腰三角形； ⑥作BC的垂直平分线交AB于I，则△BCI是等腰三角形． 故答案为：C. 【分析】根据等腰三角形的性质分情况画出图形，即可得出答案。‎ ‎7.【答案】D ‎ ‎【解析】 第一步：在已知正三角形ABC中，取AB所在的直线为x轴，取对称轴CO为y轴，画对应的x′轴、y′轴，使∠x′O′y′=45°， 第二步：在x′轴上取O′A′=OA，O′B′=OB，在y’轴上取O′C′=OC， 第三步：连接A′C′，B′C′， 所得三角形A′B′C′就是正三角形ABC的直观图， 根据画正三角形的直观图的方法可知此题选D， 故答案为：D． 【分析】根据画正三角形的直观图的方法可得出答案。‎ ‎8.【答案】D ‎ 23‎ ‎【解析】 如图，连接CD、 ， ∵在△COD和△ 中， ， ∴△COD≌△  (SSS)， ∴∠AOB= 故答案为：D。 【分析】根据全等三角形的判定方法SSS，画出三角形.‎ ‎9.【答案】D ‎ ‎【解析】 根据基本作图，所以①正确， 因为∠C=90°，∠B=30°，则∠BAC=60°，而AD平分∠BAC，则∠DAB=30°，所以∠ADC=∠DAB+∠B=60°，所以②正确； 因为∠DAB=∠B=30°，所以△ABD是等腰三角形，所有③正确； 因为AD平分∠BAC，所以点D到AB与AC的距离相等，而DC⊥AC，则点D到直线AB的距离等于CD的长度，所以④正确. 故答案为：D. 【分析】（1）由已知角的平分线的作法知，AD是∠BAC的平分线； （2）根据三角形的一个外角等于和它不相邻的两个内角的和可得∠ADC=∠DAB+∠B，由（1）可得∠DAB=30°，所以∠ADC=∠DAB+∠B=60°； （3）由（2）知，∠DAB=30°=∠B，根据等腰三角形的判定可得△ABD是等腰三角形； （4）根据角平分线上的点到角两边的距离相等可得，点D到直线AB的距离等于CD的长度。‎ ‎10.【答案】D ‎ ‎【解析】 ：用尺规作图作∠AOC=∠AOB的第一步是以点O为圆心，以任意长为半径画弧①，分别交OA、OB于点E、F， 第二步的作图痕迹②的作法是以点E为圆心，EF长为半径画弧． 故选D． 【分析】根据作一个角等于一直角的作法即可得出结论．‎ 23‎ ‎11.【答案】B ‎ ‎【解析】 ：连接EG， ∵由作图可知AD=AE，AG是∠BAD的平分线， ∴∠1=∠2， ∴AG⊥DE，OD= DE=3． ∵四边形ABCD是平行四边形， ∴CD∥AB， ∴∠2=∠3， ∴∠1=∠3， ∴AD=DG． ∵AG⊥DE， ∴OA= AG． 在Rt△AOD中，OA= = =4， ∴AG=2AO=8． 故选B． 【分析】连接EG，由作图可知AD=AE，根据等腰三角形的性质可知AG是DE的垂直平分线，由平行四边形的性质可得出CD∥AB，故可得出∠2=∠3，据此可知AD=DG，由等腰三角形的性质可知OA= AG，利用勾股定理求出OA的长即可．‎ ‎12.【答案】B ‎ ‎【解析】 ：连结EF，AE与BF交于点O，‎ ‎ ∵四边形ABCD是平行四边形，AB=AF， ∴四边形ABEF是菱形， ‎ 23‎ ‎∴AE⊥BF，OB= BF=4，OA= AE． ∵AB=5， 在Rt△AOB中，AO= =3， ∴AE=2AO=6． 故选B． 【分析】由基本作图得到AB=AF，AG平分∠BAD，故可得出四边形ABEF是菱形，由菱形的性质可知AE⊥BF，故可得出OB的长，再由勾股定理即可得出OA的长，进而得出结论．‎ 二、填空题 ‎13.【答案】同位角相等，两直线平行 ‎ ‎【解析】 如图所示：‎ ‎ 根据题意得出：∠1=∠2；∠1和∠2是同位角； ∵∠1=∠2， ∴a∥b（同位角相等，两直线平行）； 故答案为：同位角相等，两直线平行． 【分析】直尺保证了三角板 所作的是平移，∠1、∠2的大小相等，又是同位角，“同位角相等，两直线平行”.‎ ‎14.【答案】PN；PM；PN；0 ‎ ‎【解析】 ：如图 ∵PN⊥OB ‎ 23‎ ‎∴线段PN的长是表示点P到直线BO的距离； ∵PM⊥OA ∴PM的长是表示点M到直线AO的距离 ; ∵ON⊥PN ∴线段ON的长表示点O到直线PN的距离； ∵PM⊥OA ∴点P到直线OA的距离为0 故答案为：PN、PM、PN、0 【分析】先根据题意画出图形，再根据点到直线的距离的定义，即可求解。‎ ‎15.【答案】10 ‎ ‎【解析】 ：由作图可知CD是线段AB的中垂线， ∵AC=AD=BC=BD， ∴四边形ACBD是菱形， ∵AB=4，CD=5， ∴S菱形ACBD= ×AB×CD= ×4×5=10， 故答案为：10． 【分析】由作图可知CD是线段AB的中垂线，四边形ACBD是菱形，利用S菱形ACBD= ×AB×CD求解即可．‎ ‎16.【答案】‎ ‎【解析】 ：由作图可知，EF垂直平分AB，即DC是直角三角形ABC斜边上的中线， 故DC= AB= = ×15= ． 故答案为： ． 【分析】由作图可知，EF垂直平分AB，即DC是直角三角形ABC斜边上的中线，在Rt△ABC中，利用勾股定理求出AB的长，即可求得DC的长。‎ ‎17.【答案】56 ‎ ‎【解析】 ：∵四边形ABCD的矩形， ∴AD∥BC， ∴∠DAC=∠ACB=68°． ∵由作法可知，AF是∠DAC的平分线， ∴∠EAF= ∠DAC=34°． ∵由作法可知，EF是线段AC的垂直平分线， ‎ 23‎ ‎∴∠AEF=90°， ∴∠AFE=90°﹣34°=56°， ∴∠α=56°． 故答案为：56． 【分析】先根据矩形的性质得出AD∥BC，故可得出∠DAC的度数，由角平分线的定义求出∠EAF的度数，再由EF是线段AC的垂直平分线得出∠AEF的度数，根据三角形内角和定理得出∠AFE的度数，进而可得出结论．‎ ‎18.【答案】2 ‎ ‎【解析】 ：根据题中的语句作图可得下面的图，过点D作DE⊥AC于E， 由尺规作图的方法可得AD为∠BAC的角平分线， 因为∠ADB=60°， 所以∠B=90°， 由角平分线的性质可得BD=DE=2， 在Rt△ABD中，AB=BD·tan∠ADB=2 . 故答案为2 . 【分析】由尺规作图-角平分线的作法可得AD为∠BAC的角平分线，由角平分线的性质可得BD=2，又已知∠ADB即可求出AB的值.‎ ‎19.【答案】2 ；取格点M，N，连接MN交AB于P，则点P即为所求 ‎ 23‎ ‎【解析】 (Ⅰ)由勾股定理得AB= ； (Ⅱ)∵AB ，AP= ， ∴ , ∴AP:BP=2:1. 取格点M，N，连接MN交AB于P，则点P即为所求； ∵AM∥BN, ∴△AMP∽△BNP, ∴ , ∵AM=2,BN=1, ∴ , ∴P点符合题意. 故答案为：取格点M，N，连接MN交AB于P，则点P即为所求。 【分析】（Ⅰ）利用勾股定理求出AB的长。 (Ⅱ)先求出BP的长，就可得出AP:BP=2:1，取格点M，N，连接MN交AB于P，则点P即为所求，根据相似三角形的判定定理，可证得△AMP∽△BNP，得出对应边成比例，可证得AP:BP=2:1。‎ ‎20.【答案】‎ ‎【解析】【解答】连接AE，‎ ‎ 根据题意可知MN垂直平分AC ‎ 23‎ ‎∴AE=CE=3 在Rt△ADE中，AD2=AE2-DE2 AD2=9-4=5 ∵AC2=AD2+DC2 AC2=5+25=30 ∴AC= 【分析】根据作图，可知MN垂直平分AC，根据垂直平分线的性质，可求出AE的长，再根据勾股定理可求出AD的长，然后再利用勾股定理求出AC即可。‎ 三、解答题 ‎21.【答案】解：如图所示， ∵∠EAC=∠ACB， ∴AD∥CB， ∵AD=BC， ∴四边形ABCD是平行四边形， ∴AB∥CD． ‎ ‎【解析】【分析】用尺规作图即可完成作图。理由如下： 根据内错角相等，两直线平行可得AD∥CB，已知AD=BC，根据一组对边平行且相等的四边形是平行四边形可得四边形ABCD是平行四边形，根据平行四边形的性质可得AB∥CD．‎ 23‎ ‎22.【答案】（1）如图1，BO为所求作的角平分线 （2）如图2，过点O作OD⊥AB于点D， ∵∠ACB=90°，由（1）知BO平分∠ABC， ∴OC=OD，BD=BC。 ∵AC=4，BC=3 ∴AB=5，BD=3，AD=2 设CO=x，则AO=4-x，OD=x 在Rt△AOD中， ，得 ， 即点O到AB的距离为 ‎ ‎【解析】【分析】(1)以点B为圆心，任意长度为半径画弧，交BA,BC于以点，再分别以这两个交点为圆心，大于这两交点间的距离的长度为半径，画弧，两弧在角内交于一点，过B点及这点，作射线BO交AC于点哦，BO就是所求的∠ABC的平分线；（2）过点O作OD⊥AB于点D，根据角平分线上的点到角两边的距离相等得出OC=OD，BD=BC=3。根据勾股定理得出AB的长，进而得出AD的长， 设CO=x，则AO=4-x，OD=x，在Rt△AOD中，利用勾股定理得出方程，求解得出答案。‎ ‎23.【答案】（1）解：如图,作出角平分线CO; 作出⊙O. ‎ 23‎ ‎ （2）解：AC与⊙O相切． ‎ ‎【解析】【分析】（1）根据题意先作出∠ACB的角平分线，再以O为圆心，OB为半径画圆即可。 （2）根据角平分线上的点到角两边的距离相等及切线的判定定理，即可得出AC与⊙O相切。‎ ‎24.【答案】（1）解：如图所示，直线EF即为所求；      （2）解：∵四边形ABCD是菱形， ∴∠ABD=∠DBC= ∠ABC=75°，DC∥AB，∠A=∠C． ∴∠ABC=150°，∠ABC+∠C=180°， ∴∠C=∠A=30°， ∵EF垂直平分线线段AB， ∴AF=FB， ∴∠A=∠FBA=30°， ∴∠DBF=∠ABD﹣∠FBE=45° ‎ ‎【解析】【分析】（1）分别以A,B两点为圆心，大于AB长度一半的长度为半径画弧，两弧在AB的两侧分别相交，过这两个交点作直线，交AB于点E，交AD于点F，，直线EF即为所求； （2）根据菱形的性质得出∠ABD=∠DBC= ∠ABC=75°，DC∥AB，∠A=∠C．故∠ABC=150°，∠ABC+∠C=180°，∠C=∠A=30°，根据垂直平分线的性质得出AF=FB，根据等边对等角及角的和差即可得出答案。‎ 23‎ ‎25.【答案】（1）解：如图所示： （2）解：∵∠BAC=90°，∠C=30°  又∵点D在AC的垂直平分线上， ∴DA=DC， ∴∠CAD=∠C=30°， ∵∠DEA=∠BAC=90°， ∴△ABC∽△EDA． ‎ ‎【解析】【分析】（1）利用尺规作图作出AC的垂直平分线交BC于点D，交AC于点E 即可。 （2）根据垂直平分线的性质证出DA=DC，可证得∠CAD=∠C，然后根据两组角对应相等的两三角形相似，即可证得结论。‎ ‎26.【答案】（1）‎ ‎ （2）①证明：在AD上取一点F使DF=DC，连接EF， ‎ 23‎ ‎∵DE平分∠ADC， ∴∠FDE=∠CDE， 在△FED和△CDE中， DF=DC，∠FDE=∠CDE，DE=DE ∴△FED≌△CDE（SAS）， ∴∠DFE=∠DCE=90°，∠AFE=180°-∠DFE=90° ∴∠DEF=∠DEC， ∵AD=AB+CD，DF=DC， ∴AF=AB， 在Rt△AFE≌Rt△ABE（HL） ∴∠AEB=∠AEF， ∴∠AED=∠AEF+∠DEF= ∠CEF+ ∠BEF= （∠CEF+∠BEF）=90°。 ∴AE⊥DE ②解：过点D作DP⊥AB于点P， ∵由①可知，B，F关于AE对称，BM=FM， ∴BM+MN=FM+MN， 当F，M，N三点共线且FN⊥AB时，有最小值， ∵DP⊥AB，AD=AB+CD=6， ∴∠DPB=∠ABC=∠C=90°， ∴四边形DPBC是矩形， ∴BP=DC=2，AP=AB-BP=2， 在Rt△APD中，DP= = ， ∵FN⊥AB，由①可知AF=AB=4， ∴FN∥DP， ‎ 23‎ ‎∴△AFN∽△ADP ∴ ， 即 ， 解得FN= ， ∴BM+MN的最小值为 ‎ ‎【解析】【分析】（1）根据角平分的做法即可画出图.（2）①在AD上取一点F使DF=DC，连接EF；角平分线定义得∠FDE=∠CDE；根据全等三角形判定SAS得△FED≌△CDE，再由全等三角形性质和补角定义得∠DFE=∠DCE=∠AFE=90°， ∠DEF=∠DEC；再由直角三角形全等的判定HL得Rt△AFE≌Rt△ABE，由全等三角形性质得∠AEB=∠AEF，再由补角定义可得AE⊥DE. ②过点D作DP⊥AB于点P；由①可知，B，F关于AE对称，根据对称性质知BM=FM， 当F，M，N三点共线且FN⊥AB时，有最小值，即BM+MN=FM+MN=FN；在Rt△APD中，根据勾股定理得DP= = ；由相似三角形判定得△AFN∽△ADP，再由相似三角形性质得 ，从而求得FN，即BM+MN的最小值.‎ 23‎